大规模多输入多输出(MIMO, multiple-input multiple-output)技术通过在基站(BS, base station)端配置更多的天线来获得更高的频谱利用率和能源效率^[1].时分双工(TDD, time division duplex)的大规模MIMO系统可以利用信道互易性，借助上行的导频便可估计出下行的信道状态信息^[2].实际中，硬件缺陷、射频不匹配、天线间的互耦以及信道估计误差等因素，使得信道互易性不能被系统有效利用. Björnson等^[3]将硬件缺陷建模为与功率有关的加性噪声，并提出了线性最小均方误差(LMMSE, linear minimum mean square error)的信道估计方法；Petermann等^[4]和Wei等^[5]提出了基于电路理论的互耦模型；Vieira等^[6]经过实验提出了互耦的信道模型；Luo^[7]对存在信道估计误差的系统进行了分析.笔者分析了LMMSE和最小二乘(LS, least square)信道估计在硬件缺陷和射频不匹配情况下的性能.

互易性校准可以对射频不匹配进行补偿. Petermann等^[4]对比了基于硬件的自校准和基于Argos的相对校准的性能；Nishimori等^[8]提出了能够在线校准的自校准方法；Liu等^[9]为了减小校准周期而引入了大量参考天线；Wei等^[10]则是利用相邻天线间的强互耦进行校准；Luo等^[11]提出了使用有线信道作为校准反馈的方案.为了克服传统互易性校准成本高、反馈量大以及占用天线数多等缺点，笔者对BS内的相对校准方案进行了改进.为了降低和均匀校准中的互耦干扰，提出了通过天线位置预先估计互耦干扰统计特性再利用导频的功率调节来限制互耦干扰的方案.通过对均匀线性阵列(ULA, uniform linear array)和均匀圆形阵列(UCA, uniform circle array)的仿真分析可知，所提方案与传统方案相比具有优越性.

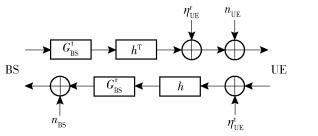
1 系统模型

实际中BS端的射频电路有着良好的散热性能，其链路响应变化缓慢，随温湿度的改变而呈分钟级变化^[12]，若忽略相位噪声，相干时间内的射频链路响应可视为常数；而用户设备(UE, user equipment)端射频电路存在散热和电源等方面的缺陷，其链路响应变化较快，使用与发射功率成正比的加性噪声来代表硬件缺陷，则链路模型如图 1所示.

若BS处有M根天线，对应的单用户MIMO系统的上下行接收信号表示为

$ {\mathit{\boldsymbol{y}}_{{\rm{UL}}}} = \mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{r}}\mathit{\boldsymbol{h}}\left( {d + \eta _{{\rm{UE}}}^{\rm{t}}} \right) + {\mathit{\boldsymbol{n}}_{{\rm{BS}}}} $

(1a)

$ {\mathit{\boldsymbol{y}}_{{\rm{DL}}}} = {\mathit{\boldsymbol{h}}^{\rm{T}}}\mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{t}}\mathit{\boldsymbol{s}} + \eta _{{\rm{UE}}}^{\rm{r}} + {n_{{\rm{UE}}}} $

(1b)

其中：$ \mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{r}} = {\rm{diag}}(g_{{\rm{BS}}}^{{{\rm{r}}_{\rm{1}}}}, g_{{\rm{BS}}}^{{{\rm{r}}_{\rm{2}}}}, \ldots , g_{{\rm{BS}}}^{{{\rm{r}}_M}})$和$\mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{t}} = {\rm{diag}}(g_{{\rm{BS}}}^{{{\rm{t}}_{\rm{1}}}}, g_{{\rm{BS}}}^{{{\rm{t}}_{\rm{2}}}}, \ldots , g_{{\rm{BS}}}^{{{\rm{t}}_M}}) $分别为BS端射频链路的接收和发射增益，在理想情况下$\mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{r}} = \mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{t}} = {\mathit{\boldsymbol{I}}_M} $，射频不匹配的情况下$ \mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{r}} \ne \mathit{\boldsymbol{G}}_{{\rm{BS}}}^{\rm{t}};\mathit{\boldsymbol{h}} \sim {\rm{CN}}({\bf{0}}, {\mathit{\boldsymbol{I}}_M})$为独立同分布的瑞利信道；d~CN(0, 1)为UE发射的导频符号，其功率为1；s=wx为经过预编码后的下行信号，w为预编码向量，x为发射给单个用户的符号；$\eta _{{\rm{UE}}}^{\rm{r}} \sim {\rm{CN}}(0, {\rm{tr}}\left( \mathit{\boldsymbol{Q}} \right)\delta _{\rm{r}}^{\rm{2}}) $及$\eta _{{\rm{UE}}}^{\rm{t}} \sim {\rm{CN}}(0, E[d{d^{\rm{H}}}]\delta _{\rm{t}}^2) $分别为UE端的硬件缺陷，3GPP的LTE标准中δ_t和δ_r与UE的误差矢量幅度有关满足δ∈[0.08, 0.175]，Q为接收信号的协方差矩阵；n_BS和n_UE分别为BS和UE处的等效热噪声，且有n_BS~CN(0, ρ^－1I_M)、n_UE~CN(0, ρ^－1)，ρ为信号的信噪比(SNR, signal noise ratio).为了方便，将G_BS^r和G_BS^t改写为G_r和G_t，η_UE^r和η_UE^t改写为η_r和η_t并与h、n_BS、n_UE和d相互独立.文中diag(·)表示对角阵，(·)^T、(·)^H、(·)^*及tr(·)分别为矩阵的转置、共轭转置、共轭和迹，E(·)和‖·‖分别表示期望和向量的范数.

2 信道估计误差 2.1 上行信道估计的误差

Björnson等^[3]提出的LMMSE信道估计方法可以减轻硬件缺陷对信道估计的影响，对于图 1所示的模型则有

$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}} = \underbrace {{d^ * }{\mathit{\boldsymbol{R}}_{{\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{h}}}}\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{y}}^{ - 1}{\mathit{\boldsymbol{y}}_{{\rm{UL}}}}}_\mathit{\boldsymbol{A}} $

(2)

其中：R_Grh和R_y分别为G_rh以及y_UL的自协方差矩阵，不计相噪，G_r在相干时间内为常数阵，由于导频的功率为1，则有

$ \mathit{\boldsymbol{A}} = \frac{{{\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{G}}_{\rm{r}}^{\rm{H}}}}{{{\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{G}}_{\rm{r}}^{\rm{H}}\left( {1 + \delta _{\rm{t}}^2} \right) + {\rho ^{ - 1}}{\mathit{\boldsymbol{I}}_M}}} $

(3)

令估计的信道为$\mathit{\boldsymbol{\tilde h}} = \mathit{\boldsymbol{Gh + \boldsymbol{\varDelta} }} $，其中Gh为真实信道，Δ为误差矢量，得到${{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}} = {\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{h}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_1} $，则有

$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}} \sim {\rm{CN}}\left( {0,\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{G}}_{\rm{r}}^{\rm{H}}\left( {1 + \delta _{\rm{t}}^2} \right) + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\rho ^{ - 1}}} \right) $

(4)

并且${\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{h}} \sim {\rm{CN}}({\bf{0}}, {\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{G}}_{\rm{r}}^{\rm{H}})、{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_1} \sim {\rm{CN}}({\bf{0}}, {\mathit{\boldsymbol{C}}_1}) $以及γ₁=tr(C₁)，其中$ {\mathit{\boldsymbol{C}}_1} = {\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{G}}_{\rm{r}}^{\rm{H}}[\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{H}}}(1 + \delta _{\rm{t}}^2) - 2\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{I}}_M}] + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\rho ^{ - 1}}$，γ₁为LMMSE信道估计的均方误差.对于LS信道估计，有${{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}} = {\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{h}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_2} $，各项满足$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}} \sim {\rm{CN}}({\bf{0}}, {\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{G}}_{\rm{r}}^{\rm{H}}(1 + \delta _{\rm{t}}^2) + {\rho ^{ - 1}}{\mathit{\boldsymbol{I}}_M})、{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_2} \sim {\rm{CN}}({\bf{0}}, {\mathit{\boldsymbol{C}}_2})$及G_rh~CN(0, G_rG_r^H)，且γ₂=tr(C₂)，其中C₂=G_rG_r^Hδ_t²+ρ^－1I_M，γ₂为LS信道估计的均方误差.

2.2 相对于下行信道的误差

TDD系统中，BS的发射和接收链路的响应不完全相同，使得相干时间内估计的信道与实际信道存在差异.忽略相噪，相干时间内G_r和G_t为常数阵，将G_r和G_t描述为加法关系G_r=G_t+Λ_a，Λ_a为diag(λ_a1, λ_a2, …, λ_aM)，各对角元素相互独立且λ_ai~CN(0, σ_a²)，σ_a为不匹配程度.此时LMMSE信道估计的线性变换矩阵改为

$ {\mathit{\boldsymbol{A}}_1} = \frac{{{\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{G}}_{\rm{t}}^{\rm{H}} + \sigma _{\rm{a}}^2{\mathit{\boldsymbol{I}}_M}}}{{\left( {{\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{G}}_{\rm{t}}^{\rm{H}} + \sigma _{\rm{a}}^2{\mathit{\boldsymbol{I}}_M}} \right)\left( {1 + \delta _{\rm{t}}^2} \right) + {\rho ^{ - 1}}{\mathit{\boldsymbol{I}}_M}}} $

(5)

$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{y}}_{{\rm{UL}}}}$经处理后，得到$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}} = {\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{h}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_3}$，其中Δ₃~CN(0, C₃)，并且${\mathit{\boldsymbol{C}}_3} = \sigma _{\rm{a}}^{\rm{2}}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{A}}_1^{\rm{H}}(1 + \delta _{\rm{t}}^2) + {\rho ^{ - 1}}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{A}}_1^{\rm{H}} + {\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{G}}_{\rm{t}}^{\rm{H}}[{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{A}}_1^{\rm{H}}(1 + \delta _{\rm{t}}^2) - 2{\mathit{\boldsymbol{A}}_1} + {\mathit{\boldsymbol{I}}_M}] $.

LS信道估计的上行信道为${{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}} = ({\mathit{\boldsymbol{G}}_{\rm{t}}} + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{\rm{a}}})\mathit{\boldsymbol{h}} + {\mathit{\boldsymbol{n}}_{{\rm{BS}}}} + ({\mathit{\boldsymbol{G}}_{\rm{t}}} + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{\rm{a}}})\mathit{\boldsymbol{h}}{\eta _{\rm{t}}} $，改写为${{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}} = {\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{h}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_4} $，其中Δ₄~CN(0, C₄)，误差的协方差矩阵为${\mathit{\boldsymbol{C}}_4} = {\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{G}}_{\rm{t}}^{\rm{H}}\delta _{\rm{t}}^2 + \sigma _{\rm{a}}^2{\mathit{\boldsymbol{I}}_M}(1 + \delta _{\rm{t}}^2) + {\rho ^{ - 1}}{\mathit{\boldsymbol{I}}_M} $.

3 信道容量

TDD系统中，系统将估计出的上行信道用于上行信号的检测，此后又将其应用于下行的预编码，因此信道估计直接影响着整个系统的性能，下面将分析信道估计对上下行信道容量的影响.

3.1 上行信道容量

利用2.1节中的结论，得到以下关系：

$ {\mathop{\rm var}} \left( {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}}} \right) \approx {\mathop{\rm var}} \left( {{\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{h}}} \right) + {\mathop{\rm var}} \left( {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_1}} \right) $

(6a)

$ {\mathop{\rm var}} \left( {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}}} \right) \approx {\mathop{\rm var}} \left( {{\mathit{\boldsymbol{G}}_{\rm{r}}}\mathit{\boldsymbol{h}}} \right) + {\mathop{\rm var}} \left( {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_2}} \right) $

(6b)

设G_r=I_M，则A=I_M/(1+δ_t²+ρ^－1)，由于存在cov (G_rh, Δ₁)=(δ_t²+ρ^－1)/(1+δ_t²+ρ^－1)I_M≠0，选择分析高SNR的情况，则G_rh和Δ₁接近相互独立.简化估计的信道为

$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}} = \sqrt {1/\left( {1 + {\tau _{{\rm{LM}}}}} \right)} \mathit{\boldsymbol{h}} + \sqrt {{\tau _{{\rm{LM}}}}/\left( {1 + {\tau _{{\rm{LM}}}}} \right)} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_1} $

(7)

其中$ \sqrt {1/(1 + {\tau _{{\rm{LM}}}})} $及$ \sqrt {{\tau _{{\rm{LM}}}}/(1 + {\tau _{{\rm{LM}}}})} $分别表示实际信道和误差的加权系数，τ_LM为误差与实际信道功率的比值：

$ {\tau _{{\rm{LM}}}} = \frac{{{\rm{tr}}\left( {{\mathit{\boldsymbol{C}}_1}} \right)}}{{{\rm{tr}}\left[ {E\left( {\mathit{\boldsymbol{h}}{\mathit{\boldsymbol{h}}^{\rm{H}}}} \right)} \right]}} = \frac{{{\gamma _1}}}{M} = \frac{{\delta _{\rm{t}}^2 + {\rho ^{ - 1}}}}{{1 + \delta _{\rm{t}}^2 + {\rho ^{ - 1}}}} $

(8)

对于LS信道估计，有

$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}} = \sqrt {1/\left( {1 + {\tau _{{\rm{LS}}}}} \right)} \mathit{\boldsymbol{h}} + \sqrt {{\tau _{{\rm{LS}}}}/\left( {1 + {\tau _{{\rm{LS}}}}} \right)} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_2} $

(9)

其中：

$ {\tau _{{\rm{LS}}}} = \frac{{{\rm{tr}}\left( {{\mathit{\boldsymbol{C}}_2}} \right)}}{{{\rm{tr}}\left[ {E\left( {\mathit{\boldsymbol{h}}{\mathit{\boldsymbol{h}}^{\rm{H}}}} \right)} \right]}} = \frac{{{\gamma _2}}}{M} = \delta _{\rm{t}}^2 + {\rho ^{ - 1}} $

(10)

接收的上行信号为y_UL=h(s+η_t)+n_BS，其中s~CN(0, 1)为UE发送的数据符号，且与导频d具有相同的SNR.上行的信号检测为$\mathit{\boldsymbol{\hat y}} = \mathit{\boldsymbol{\omega }}{\mathit{\boldsymbol{y}}_{{\rm{UL}}}} $，其中ω为信号检测向量.常见的线性信号检测有最大比合并(MRC, maximum ratio combining)、迫零(ZF, zero forcing)和最小均方误差(MMSE, minimum mean squared error)，信号检测向量分别如式(11)所示，三者均含有$ {{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}$，唯独系数不同.如ZF信号检测的系数为${({{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}\mathit{\boldsymbol{\tilde h}})^{ - 1}} $，这些系数使得有用与无用信号的功率同时被放大或缩小，故在单用户情况下3种信号检测后的信号与干扰加噪声比(SINR, signal to interference plus noise ratio)相等.

$ \left. \begin{array}{l} {{\mathit{\boldsymbol{\tilde \omega }}}_{{\rm{MRC}}}} = {{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}\\ {{\mathit{\boldsymbol{\tilde \omega }}}_{{\rm{ZF}}}} = {\left( {{{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}\mathit{\boldsymbol{\tilde h}}} \right)^{ - 1}}{{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}\\ {{\mathit{\boldsymbol{\tilde \omega }}}_{{\rm{MMSE}}}} = {\left( {{{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}\mathit{\boldsymbol{\tilde h}} + {\rho ^{ - 1}}} \right)^{ - 1}}{{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}} \end{array} \right\} $

(11)

选择典型的MRC信号检测，则有

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat y}} = {{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}\mathit{\boldsymbol{\tilde h}}s + {{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}\mathit{\boldsymbol{\tilde h}}{\eta _{\rm{t}}} + {{\mathit{\boldsymbol{\tilde h}}}^{\rm{H}}}{\mathit{\boldsymbol{n}}_{{\rm{BS}}}} = }\\ {\sqrt {1/1 + \tau } \left( {{\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{h}}s + {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{h}}{\eta _{\rm{t}}} + {\mathit{\boldsymbol{h}}^{\rm{H}}}{\mathit{\boldsymbol{n}}_{{\rm{BS}}}}} \right) + }\\ {\sqrt {\tau /1 + \tau } \left( {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}^{\rm{H}}}\mathit{\boldsymbol{h}}s + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}^{\rm{H}}}\mathit{\boldsymbol{h}}{\eta _{\rm{t}}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}^{\rm{H}}}{\mathit{\boldsymbol{n}}_{{\rm{BS}}}}} \right)} \end{array} $

(12)

得到

$ \begin{array}{*{20}{c}} {{\rm{tr}}\left( {E\left( {\mathit{\boldsymbol{\hat y}}{{\mathit{\boldsymbol{\hat y}}}^{\rm{H}}}} \right)} \right) = \sqrt {1/1 + \tau } \left( {{M^2} + {M^2}\delta _{\rm{t}}^2 + M{\rho ^{ - 1}}} \right) + }\\ {\sqrt {\tau /1 + \tau } \gamma \left( {1 + \delta _{\rm{t}}^2 + {\rho ^{ - 1}}} \right)} \end{array} $

(13)

其中γ为LMMSE或LS信道估计的均方误差；τ为LMMSE或LS信道估计误差与实际信道的比值.将有用与无用信号分开，得到式(14)和式(15)，其中$\mathfrak{R}_{{\rm{UL}}}$为上行导频的SINR；C^UL为上行信道容量.可见$\mathfrak{R}_{{\rm{UL}}}$与ρ、BS端天线个数M、UE处硬件缺陷程度δ_t以及使用的信道估计方式τ有关.信道容量为ρ与M的增函数，对δ_t表现为减函数的性质，大规模MIMO天线数可达数百甚至更多，极大地提高了上行的信道容量，而严重的硬件缺陷则会降低信道容量.

$ \begin{array}{*{20}{c}} {{\Re _{{\rm{UL}}}} = \frac{{{M^2}}}{{{M^2}\delta _{\rm{t}}^2 + M{\rho ^{ - 1}} + \tau \gamma \left( {1 + \delta _{\rm{t}}^2 + {\rho ^{ - 1}}} \right)}} = }\\ {{{\left[ {\delta _{\rm{t}}^2 + \frac{{{\rho ^{ - 1}}}}{M} + \frac{{{\tau ^2}}}{M}\left( {1 + \delta _{\rm{t}}^2 + {\rho ^{ - 1}}} \right)} \right]}^{ - 1}}} \end{array} $

(14)

$ {C^{{\rm{UL}}}} = {\rm{lb}}\left( {1 + {\Re _{{\rm{UL}}}}} \right) $

(15)

令ρ与M为无穷大，则信道容量上限为C_max^UL=lb(1+δ_t^－2)，可见UE处存在的硬件缺陷使得信道容量难以达到理想状态.

3.2 下行信道容量

上文分析了估计误差与射频不匹配的关系，得到如下关系：

$ {\rm{var}}\left( {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}}} \right) \approx {\rm{var}}\left( {{\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{h}}} \right) + {\rm{var}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_3}} \right) $

(16a)

$ {\rm{var}}\left( {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}}} \right) = {\rm{var}}\left( {{\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{h}}} \right) + {\rm{var}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_4}} \right) $

(16b)

设G_t=I_M，则${\mathit{\boldsymbol{A}}_1} = (1 + \sigma _{\rm{a}}^{\rm{2}}){\mathit{\boldsymbol{I}}_M}/((1 + \delta _{\rm{t}}^2)(1 + \sigma _{\rm{a}}^{\rm{2}}) + {\rho ^{ - 1}}), {\rm{cov}}({\mathit{\boldsymbol{G}}_{\rm{t}}}\mathit{\boldsymbol{h}}, {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_3}) = {\mathit{\boldsymbol{I}}_M}(1 - (1 + \sigma _{\rm{a}}^{\rm{2}})/((1 + \sigma _{\rm{a}}^{\rm{2}})(1 + \delta _{\rm{t}}^2) + {\rho ^{ - 1}})) $使式(16a)不相等，为了使G_th与Δ₃接近相互独立，选择分析δ_t较小和高SNR的情况.同理，$ {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LMMSE}}}} = \sqrt {1/1 + {\kappa _{{\rm{LM}}}}} \mathit{\boldsymbol{h}} + \sqrt {{\kappa _{{\rm{LM}}}}/1 + {\kappa _{{\rm{LM}}}}} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_3}, {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{LS}}}} = \sqrt {1/1 + {\kappa _{{\rm{LS}}}}} \mathit{\boldsymbol{h}} + \sqrt {{\kappa _{{\rm{LS}}}}/1 + {\kappa _{{\rm{LS}}}}} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_4}$

$ {\kappa _{{\rm{LM}}}} = \frac{{\sigma _{\rm{a}}^4 - 1}}{{\left( {1 + \sigma _{\rm{a}}^2} \right)\left( {1 + \delta _{\rm{t}}^2} \right) + {\rho ^{ - 1}}}} + 1 $

(17)

$ {\kappa _{{\rm{LS}}}} = \delta _{\rm{t}}^2 + \sigma _{\rm{a}}^2\left( {1 + \delta _{\rm{t}}^2} \right) + {\rho ^{ - 1}} $

(18)

假设上下行SNR相同，接收的下行信号为y_DL=h^Twx+η_r+n_UE，其中，w=α^－1w_△为下行归一化的预编码向量，α=‖w_△‖₂为功率约束系数，w_△为预编码向量.常见的线性预编码有最大比发送(MRT, maximum ratio transmission)、ZF和MMSE，预编码向量分别如式(19)所示，三者均含有${{\mathit{\boldsymbol{\tilde h}}}^ * } $，但系数不同.根据范数的性质‖ca‖=c‖a‖，则单用户MIMO经过各预编码后的SNR相等，故选取具代表性的MRT进行分析.

$ \left. \begin{array}{l} {\mathit{\boldsymbol{w}}_{{\rm{MRT}}}} = {{\mathit{\boldsymbol{\tilde h}}}^ * }\\ {\mathit{\boldsymbol{w}}_{{\rm{ZF}}}} = {{\mathit{\boldsymbol{\tilde h}}}^ * }{\left( {{{\mathit{\boldsymbol{\tilde h}}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde h}}}^ * }} \right)^{ - 1}}\\ {\mathit{\boldsymbol{w}}_{{\rm{MMSE}}}} = {{\mathit{\boldsymbol{\tilde h}}}^ * }{\left( {{{\mathit{\boldsymbol{\tilde h}}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde h}}}^ * } + {\rho ^{ - 1}}} \right)^{ - 1}} \end{array} \right\} $

(19)

利用估计与实际信道的功率关系

$ \left\| {\mathit{\boldsymbol{\tilde h}}} \right\|_2^2 = \left( {1 + \kappa } \right)\left\| \mathit{\boldsymbol{h}} \right\|_2^2 $

则有功率约束系数$\alpha = \parallel \mathit{\boldsymbol{\tilde h}}{\parallel _2} = \sqrt {\left( {1 + \kappa } \right)M} $，接收的信号为

$ \begin{array}{l} {\mathit{\boldsymbol{y}}_{{\rm{DL}}}} = \left\| {{{\mathit{\boldsymbol{\tilde h}}}^ * }} \right\|_2^{ - 1}{{\mathit{\boldsymbol{\tilde h}}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde h}}}^ * }x + {\eta _{\rm{r}}} + {n_{{\rm{UE}}}} = \\ \sqrt {1/\left( {1 + \kappa } \right)M} \sqrt {1/1 + \kappa } {\mathit{\boldsymbol{h}}^{\rm{T}}}{\mathit{\boldsymbol{h}}^ * }x + {\eta _{\rm{r}}} + \\ \sqrt {1/\left( {1 + \kappa } \right)M} \sqrt {\kappa /1 + \kappa } {\mathit{\boldsymbol{h}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}^ * }x + {n_{{\rm{UE}}}} \end{array} $

(20)

同理，${\rm{tr}}[E({\mathit{\boldsymbol{y}}_{{\rm{DL}}}}\mathit{\boldsymbol{y}}_{{\rm{DL}}}^{\rm{H}})] = \frac{{M + {\kappa ^2}}}{{{{\left( {1 + \kappa } \right)}^2}}} + \frac{{M + {\kappa ^2}}}{{{{\left( {1 + \kappa } \right)}^2}}}\delta _{\rm{r}}^{\rm{2}}r + {\rho ^{ - 1}} $，其中κ为LMMSE或LS信道估计误差与实际下行信道的比值.提取有用与无用信号得出下行信号的SINR(见式(21))和下行信道容量(见式(22))，下行的信道容量与ρ、M、δ_t、δ_r、射频不匹配程度σ_a和估计方式κ有关，为ρ与M的增函数，对δ_t、δ_r和σ_a表现为减函数的性质.

$ {\Re _{{\rm{DL}}}} = \frac{M}{{{\kappa ^2} + \left( {M + {\kappa ^2}} \right)\delta _{\rm{r}}^2 + {{\left( {1 + \kappa } \right)}^2}{\rho ^{ - 1}}}} $

(21)

$ {C^{{\rm{DL}}}} = {\rm{lb}}\left( {1 + {\Re _{{\rm{DL}}}}} \right) $

(22)

令ρ与M为无穷大，则C_max^DL=lb(1+δ_r^－2)，可见UE处的硬件缺陷使得信道容量达不到理想状态.

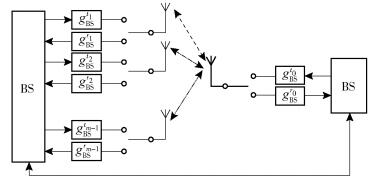
4 互易性校准

互易性校准可以消除射频不匹配的影响. Wei等^[10]将已校准天线作为参考天线对其余天线校准，使得误差在传递过程中被扩大，需要限制这种传递关系的延续.文献[9]中过多的天线参与校准会影响BS吞吐量和覆盖范围.针对上述问题，利用大规模MIMO系统天线数庞大的特点，选取少量天线参与校准对系统性能影响甚微.如图 2所示，在BS内选取一根参数良好的参考天线，分别对其余天线校准，在校准时除了被校和参考天线，其余天线正常工作，以保证文献[8]中的在线校准要求.若BS天线射频链路增益为各子载波的连续函数，可以选取具代表性的子载波进行校准.由于链路不同，各天线选取的子载波也不同.此外，增益函数是时变的，校准不是一劳永逸的.在执行校准时，校准子载波上的导频会对同频子载波上的用户数据造成干扰，为此BS需要避免将用于校准的子载波分配给用户.

4.1 互耦干扰模型

校准时，工作中的天线发射信号会对校准天线有互耦干扰，根据天线间耦合强度随间距的增大递减，以及阵列天线间的互耦信道模型^[6]，对互耦干扰作如下假设：①工作中阵元功率放大器的噪声会耦合至其他阵元上^[13]，将互耦干扰建立为加性的噪声^[14]，使用零均值复高斯分布的加性噪声表示校准时的互耦干扰；②互耦干扰强度与干扰信号源强度有关，设加性噪声的方差与干扰天线发射功率成正比；③天线间距增加，互耦干扰降低，设互耦干扰与距离的x次幂成反比.

改写g_BS^t_n和g_BS^r_n为t_n和r_n，设参考天线的编号为0，则对n号天线的校准有${y_{0 \to n}} = {r_n}(h{t_0}d + {v_{\rm{a}}}) + {n_n} $和$ {y_{n \to 0}} = {r_0}(h{t_n}d + {v_{\rm{b}}}) + {n_0}$.其中，h为校准天线间的信道，n_n和n₀分别为n和0号天线处的等效热噪声，v_a和v_b分别为其他天线对n号和0号天线的互耦干扰，d~CN(0, 1)为发送的校准导频.由于BS处功率放大器和低噪声放大器倍率高，存在最大接收功率的限制，校准导频功率须远小于其他天线的功率. Vieira等^[6]并未分析小功率发射情况下的互耦信道模型，故不确定小功率情况下的互耦信道.笔者假设小功率情况下校准天线间近似于视距信道，衰减很小，各对校准天线间的h近似相同.令BS内工作中的各天线功率相等且参数相同，则v_a和v_b分别满足

$ {v_{\rm{a}}} \sim {\rm{CN}}\left( {0,\beta P\sum\limits_{i \ne 0,n}^{M - 1} {l_i^{ - x}} } \right) $

(23a)

$ {v_{\rm{b}}} \sim {\rm{CN}}\left( {0,\beta P\sum\limits_{j \ne 0,n}^{M - 1} {l_j^{ - x}} } \right) $

(23b)

其中：x为实际拟合的参数，仿真中设置为2；β为与天线参数有关的系数；P为工作中的天线发射功率，仿真中假设βP=1；l_i和l_j分别为其他天线与被校和参考天线的距离.忽略热噪声的影响，则有$ {y_{0 \to n}} = {r_n}(h{t_0}d + {v_{\rm{a}}})$以及${y_{n \to 0}} = {r_0}(h{t_n}d + {v_{\rm{b}}}) $.在校准中LS信道估计更具优势，其估计的信道为$ {{\tilde h}_{0 \to n}} = {r_n}(h{t_0} + {v_{\rm{a}}})$以及$ {{\tilde h}_{n \to 0}} = {r_0}(h{t_n} + {v_{\rm{b}}})$.

为了使参考与被校天线受到互耦干扰的影响相同，BS可以利用天线位置和互耦干扰模型估计出干扰的统计特性，再通过导频的功率控制，使参考与被校天线接收信号的信号干扰比(SIR, signal to interference ratio)相等，且足够大.使用导频功率控制后的LS信道估计为$ {{\tilde h}_{0 \to n}} = {r_n}(h{t_0} + {v_{\rm{a}}}/\sqrt {{p_1}} )$和${{\tilde h}_{n \to 0}} = {r_0}(h{t_n} + {v_{\rm{b}}}/\sqrt {{p_2}} ) $，其中p₁、p₂为参考与被校天线间的导频功率，为了使SIR相等，需要满足${\rm{var}}({v_{\rm{a}}})/{p_1} = {\rm{var}}({v_{\rm{b}}})/{p_2} $.

BS将参考天线得出的估计值通过其内部电路发送给被校天线，以减轻反馈对无线资源的占用，得到对应的ZF或MMSE预编码的校准系数，如式(24)所示.一般假设参考天线满足r₀/t₀=1，这里假设r₀=t₀=1，无干扰情况下的校准系数为c_n=t_n/r_n；一般情况下校准系数如式(25)所示，其中ξ₁~CN(0, σ_a²)及ξ₂~CN(0, σ_a²)相互独立，σ_a为射频不匹配程度.

$ {c_n} = \frac{{{r_0}{t_n} + {v_{\rm{b}}}/\left( {h\sqrt {{p_2}} } \right)}}{{{r_n}{t_0} + {v_{\rm{a}}}/\left( {h\sqrt {{p_1}} } \right)}} $

(24)

$ {c_n} = \frac{1}{{1 + {\xi _1}}}\frac{{1 + {\xi _2} + {v_{\rm{b}}}/\left( {h\sqrt {{p_2}} } \right)}}{{1 + {v_{\rm{a}}}/\left( {h\sqrt {{p_1}} } \right)}} $

(25)

4.2 UCA的校准

UCA各天线的间距表示为

$ \mathop {{l_{ij}}}\limits_{i,j \in \left[ {0,M - 1} \right]} = \frac{\mathit{\Theta }}{{\lambda /2}}\sin \left( {\frac{{{\rm{ \mathsf{ π} }}i}}{M} - \frac{{{\rm{ \mathsf{ π} }}j}}{M}} \right) $

(26)

其中：λ为波长，Θ为UCA的直径，i和j为天线编号.根据圆的对称性，每一对校准天线受到的互耦干扰相同，各对之间受到的干扰不同.为了使互耦干扰最小，提出如下方案：①BS初始化，设置各天线的位置并编号，其中0号为参考天线；②利用互耦干扰模型，得出各天线互耦干扰的方差；③查找最小的互耦干扰v_min，最先校准，并分配合适的导频功率p_ini；④互耦干扰为v_other的情况下，则分配导频功率为p_other=p_inivar (v_other)/var (v_min).

4.3 ULA的校准

对于ULA，参考天线可置于阵列中间(位置1)或任意一端(位置2).不同于UCA，每一对校准天线受到的互耦干扰不再相等，但4.2节中的方案仍然适用.

由表 1可知，最大与最小导频功率的比值较小，功率控制范围并不大，这使上述方案可行.

5 仿真分析

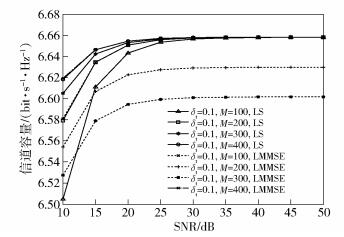
图 3所示为上行信道容量与SNR的关系.由图 3可知，当天线数M增加时，LS和LMMSE 2种估计的信道容量均有所提升；随着SNR和M的增加，UE处的硬件缺陷δ_t使得信道容量最终趋于常数.经过微调δ_t的值，发现上行信道容量对UE处的硬件缺陷很敏感：δ_t每增加10^－3，对应的信道容量下降0.03bit·s^-1·Hz^-1.在SNR为15dB的情况下，δ_t=0.1且M=100使用LS信道估计比δ_t=0.101且M=200使用LMMSE信道估计的信道容量高0.05bit·s^-1·Hz^-1. SNR在10~20dB之间时，天线数小的系统上行信道容量增长反而更快，这意味着UE处的硬件缺陷制约了MIMO系统天线数量的优势.

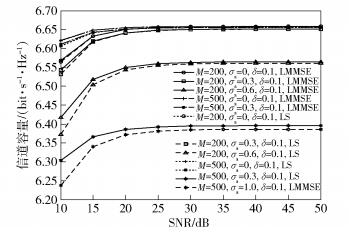
图 4为δ_t=δ_r时下行信道容量与射频链路不匹配的关系.图中信道容量随着σ_a的增大而降低，σ_a=1、M=500比σ_a=0.6、M=200情况下的信道容量少0.15bit·s^-1·Hz^-1，因而射频链路不匹配制约了天线数量的优势，进行互易性校准是必要的.

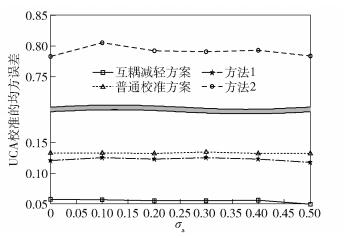
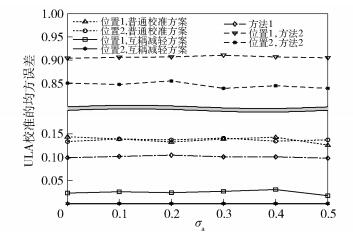
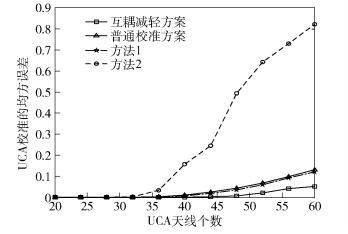
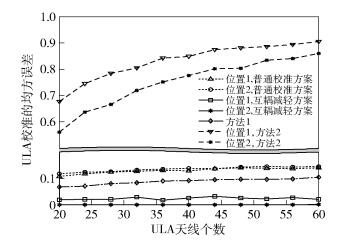
图 5所示为在Θ=10λ时各天线间距为λ/2，UCA固定SIR为5dB时各校准方案的误差与射频不匹配的关系.其中，普通校准为不使用导频功率控制的常规校准方案，方法1为使用多个参考天线的校准方法^[9]，方法2为将已校准天线作为参考天线的校准方法^[10].图 6所示为ULA固定SIR为5dB时，各校准方案的误差与射频不匹配的关系. UCA和ULA 2种阵列中，互耦减轻方案的误差最小，始终低于0.06；方法2的误差最大，介于0.75~0.9之间.图 6中，无论参考天线置于ULA的中间还是一端，普通校准的误差无明显差别；互耦减轻方案和方法2在参考天线置于中间时误差更大.根据表 1，对于互耦减轻方案，参考天线置于位置2需要更大的功率调节范围；同时，当ULA天线数增加时，位置1和位置2的校准耗能都会增加，而位置2的耗能相对较小.因此，对于ULA，参考天线置于位置2处的校准误差和能耗更小但要求更大的功率控制范围.对比图 5和图 6，除了方法2外，其他3种方案的误差均低于0.2，ULA的校准误差始终低于UCA；方法1的校准误差始终位于普通校准和互耦减轻方案之间；普通校准方案在2种阵列中校准误差均接近0.15.图 7所示为Θ=10λ的UCA中各校准方案误差与天线数目的关系.随着UCA天线数的增加，校准的误差也增加，互耦减轻方案的性能始终优于其他校准方案.从图 8可见，随着ULA天线数的增加，其他校准方案的误差也增加，而互耦减轻方案的误差比较稳定.

综上，方法2适用于其他天线不工作的情况，并不适合在线校准；方法1使用多根参考天线，提高了校准的速度和精度，但降低了BS的吞吐量；普通校准方案则牺牲了校准速度以保障BS的吞吐量，其校准精度低于方法1；而互耦减轻方案通过在普通校准方案的基础上增加导频的功率控制，同时保障了在线校准的精度和BS的吞吐量.

6 结束语

笔者分析了UE处的硬件缺陷对信道估计的影响，发现上行信道容量对UE处硬件缺陷很敏感，并通过建立上下行射频链路响应间的关系，分析了射频不匹配对下行信道容量的影响.经过仿真发现，UE处的硬件缺陷和BS处的射频不匹配都会制约大规模MIMO多天线的优势.集中式MIMO中互耦的影响是一直存在的，笔者仅考虑了其对互易性校准的影响.为了降低和均匀校准中的互耦干扰，提出了通过提前预知干扰的统计特性再通过导频的功率控制来减轻校准中互耦干扰的方案，对比各方案的均方误差，发现互耦减轻方案在精度上更具优势.