2. 西安交通大学 电子与信息工程学院, 西安 710049
针对传统预测模型已不再适用于卫星网络的问题,提出了一种自适应步长和自适应核宽度的核最小均方算法(AKLMS).通过核函数将非线性数据从低维输入空间映射到高维特征空间进行操作,并且在迭代过程中根据瞬时误差自适应地调整步长和核宽度.仿真结果证明,与核最小均方算法(KLMS)和最小均方算法(LMS)相比,AKLMS算法在收敛速度和预测流量精度方面都有大幅提升,为卫星网络的流量规划和路由设计提供了强有力的决策支持.
2. School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China
Due to the resource limitation and topology change in satellite network, the article puts forward higher requirements for the accuracy and efficiency of the network traffic prediction algorithm, and the traditional prediction model is no longer suitable for the satellite network. The author presents a kernel least mean square algorithm (KLMS) with adaptive step length and adaptive kernel width, namely AKLMS, which maps the nonlinear data from low dimensional input space to high dimensional feature space through kernel function, and the algorithm will adaptively adjust the step length and kernel width based on the instantaneous error in the iterative process. Simulations show that the AKLMS algorithm has great improvement on the convergence speed and prediction accuracy of the flow compared with the KLMS and least mean square (LMS), which will provide strong decision support for traffic planning and routing design in satellite network.
空天地一体化信息网络是由通信、侦察、导航、气象等多种功能的异构卫星网络、深空网络、空间飞行器以及地面有线和无线网络设施组成,它通过星间链路和星地链路将地面、海上、空中和深空中的用户、飞行器以及各种通信平台密集联合,是目前的研究热点之一.而卫星网络作为其骨干部分,具有全球覆盖、接入简单、支持多种业务等诸多优点,在全球通信、导航定位、气象预测、环境与灾害监测、资源探测和军事应用等领域发挥越来越重要的作用.
由于卫星网络带宽资源的限制,经过优化的流量分配方法可以提升卫星网络的利用率,因此流量规划问题成为卫星通信网络系统设计中极为关键的部分[1].近年来,基于卫星网络流量预测的路由算法也成为卫星网络路由技术研究的热点之一[2-3],其中所使用的卫星流量预测算法在预测精度和效率以及算法复杂度等方面各有优劣.
目前,很多网络流量模型已被提出,如时间序列预测模型、灰色预测模型、单一神经网络预测模型、互相关熵预测模型[4-5]等,它们直接应用于卫星网络的效果都不太理想.目前,针对卫星网络的流量预测研究也逐渐增多[6-7],其中以神经网络为基础的组合预测模型以其强大的容错性、快速并行的计算和强大的学习能力,在网络流量预测方面取得了较好的效果.但其在神经网络模型、层结构、神经节点数量以及训练方式的选择上都没有明确的理论依据,选择这些参数时只能依靠经验,且在神经网络应用程序开发中的算法复杂度也是一个瓶颈.
相反,最小均方(LMS,least mean square)算法作为自适应算法的典型代表,具有较低的算法复杂度.核函数作为目前的一个研究热点,得到了广泛的关注,它可以通过内积运算将低维输入空间中的非线性数据映射到高维特征空间.其中基于核函数的机器学习算法已成功地应用于模式识别、人工智能和信号处理等方面.特别是Liu等[8]提出了基于LMS的核最小均方(KLMS,kernel-LMS)算法,其基本思想是在基于内核的特征空间上执行LMS算法. KLMS算法将权重更新过程定义成内积的形式,使输入空间的计算更加方便. Zhao等[9]成功地将KLMS算法应用到网络流量预测方面,可以看到,KLMS算法与LMS算法相比在收敛速度和精度方面有所提高.但卫星网络对算法收敛速度和精度有着更加苛刻的要求.考虑到卫星网络的这些特性,提出了一种自适应步长和自适应核宽度的核最小均方(AKLMS,adaptive step length and adaptive kernel width kernel LMS)算法,将步长和核宽度在迭代过程中根据瞬时误差的变化进行自适应地调整,而非固定于某一个值.仿真实验将AKLMS与KLMS和LMS在收敛速度和预测误差方面进行了比较,验证了AKLMS的性能优势.
1 AKLMS算法LMS算法是基于自适应理论的,它使用随机梯度算法迭代权系数,直到均方误差(MSE,mean squared error)达到最小值为止.在迭代过程中不需要求相关函数和逆矩阵,计算简单,广泛应用于各工程领域.其数学描述为
| $ \mathop {\min }\limits_\mathit{\boldsymbol{w}} = E{\left( {y - {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{u}}} \right)^2} $ | (1) |
其中:y表示期望输出结果,w表示权系数,u表示输入向量. LMS算法的更新过程为
| $ {\mathit{\boldsymbol{w}}_0} = 0,n = 1 $ | (2a) |
| $ {e_n} = {y_n} - \mathit{\boldsymbol{w}}_{n - 1}^{\rm{T}}{\mathit{\boldsymbol{u}}_n} $ | (2b) |
| $ {\mathit{\boldsymbol{w}}_n} = {\mathit{\boldsymbol{w}}_{n - 1}} + \mu {e_n}{\mathit{\boldsymbol{u}}_n} $ | (2c) |
| $ {y_n} = \mathit{\boldsymbol{w}}_n^{\rm{T}}{\mathit{\boldsymbol{u}}_n} $ | (2d) |
| $ n = n + 1 $ | (2e) |
其中:μ表示权系数的更新步长,且μ>0,w0为权系数的初始值,en为第n次的迭代误差.可以设置一个阈值ε,当迭代误差小于ε时,终止迭代.
核函数可以有效地解决非线性问题,它通过一个非线性映射,可以将原始数据映射到高维特征空间,完成非线性到线性的转换,并在高维特征空间对数据进行线性分析和处理.其中高斯核函数是使用最为广泛的核函数.高斯核函数为
| $ {\kappa _\sigma }\left( {x - y} \right) = \exp \left( { - \frac{{{e^2}}}{{2{\sigma ^2}}}} \right) $ | (3) |
其中:e=x-y,σ表示核宽度且σ>0.
基于高斯核函数的最大互相关熵准则(MCC, maximum correntropy criterion)可以提高滤波器的鲁棒性[10-12].所以在AKLMS算法的权系数迭代过程中不仅使用高斯核函数进行数据映射,还引入MCC准则,可增强AKLMS算法的鲁棒性[13]. AKLMS算法的权系数迭代公式为
| $ {\mathit{\boldsymbol{w}}_n} = {\mathit{\boldsymbol{w}}_{n - 1}} + \frac{\mu }{{\sigma _n^2}}\exp \left( { - \frac{{e_n^2}}{{\sigma _n^2}}} \right){e_n}{\mathit{\boldsymbol{u}}_n} $ | (4) |
在上述的权系数迭代过程中,核宽度是影响算法收敛速度和鲁棒性的重要因素.当核宽度较大时,算法收敛速度加快,但易受噪声影响.当核宽度较小时,算法鲁棒性较强,但收敛速度缓慢,特别是当权系数初始值远离最优权系数时.而自适应地更新核宽度可以解决上述问题[13],既可以保证算法的鲁棒性,又可以提高算法的收敛性能.自适应更新核宽度的权系数过程为
| $ \sigma _n^2 = e_n^2 + {\sigma ^2} $ | (5a) |
| $ {\mathit{\boldsymbol{w}}_n} = {\mathit{\boldsymbol{w}}_{n - 1}} + \frac{\mu }{{\sigma _n^2}}\exp \left( { - \frac{{e_n^2}}{{\sigma _n^2}}} \right){e_n}{\mathit{\boldsymbol{u}}_n} $ | (5b) |
其中:σn根据迭代瞬时误差自适应地调整核宽度,以保证算法在收敛性能和鲁棒性方面的性能优势;σ为基于某种方法或经验选择的基准核宽度.
步长μ也是影响AKLMS算法收敛性能和预测精度的重要因素.在固定步长算法中,当步长较大时,虽然算法前期收敛速度快,但当权系数接近最佳时已收敛的曲线会出现波动,影响算法的稳定性.当步长较小时,虽然能保证算法的稳定性,但算法整体的收敛速度较慢,特别是当权系数远离最优值时.覃等[14]提出了自适应调整步长的LMS算法,将步长μn作为误差en的Sigmoid函数.笔者将此应用到AKLMS算法中,步长自适应过程为
| $ {\mu _n} = \beta \left( {\frac{1}{{1 + \exp \left( { - \alpha \left| {{e_n}} \right|} \right)}} - 0.5} \right) $ | (6) |
其中:α为控制S型函数形状的常数;β为控制S型函数范围的常数. μn根据迭代瞬时误差自适应地调整步长,以保证算法在收敛性能和稳定性方面的性能优势.
综上所述,AKLMS算法的迭代过程为
| $ {\mathit{\boldsymbol{w}}_0} = 0,n = 1 $ | (7a) |
| $ {e_n} = {y_n} - \mathit{\boldsymbol{w}}_{n - 1}^{\rm{T}}{\mathit{\boldsymbol{u}}_n} $ | (7b) |
| $ \sigma _n^2 = e_n^2 + {\sigma ^2} $ | (7c) |
| $ {\mu _n} = \beta \left( {\frac{1}{{1 + \exp \left( { - \alpha \left| {{e_n}} \right|} \right)}} - 0.5} \right) $ | (7d) |
| $ {\mathit{\boldsymbol{w}}_n} = {\mathit{\boldsymbol{w}}_{n - 1}} + \frac{{{\mu _n}}}{{\sigma _n^2}}\exp \left( { - \frac{{e_n^2}}{{\sigma _n^2}}} \right){e_n}{\mathit{\boldsymbol{u}}_n} $ | (7e) |
| $ {y_n} = \mathit{\boldsymbol{w}}_n^{\rm{T}}{\mathit{\boldsymbol{u}}_n} $ | (7f) |
| $ n = n + 1 $ | (7g) |
经过分析可知,AKMLS算法具有以下的理论优势.首先它使用高斯核函数,可以解决数据的非线性问题,将原始数据通过核函数的非线性映射映射到高维特征空间,有效地将非线性数据转化为线性数据,方便后续数据的处理分析.然后相比于LMS和KLMS算法,AKLMS算法的步长和核宽度都是自适应的,步长和核宽度不再固定在一个值上,而是根据迭代误差自动调整.当权系数远离最优解时,迭代过程会产生较大的迭代误差,从而在下一次迭代时,步长和核宽度都会变大,加快收敛速度.当权系数接近最优解时,迭代过程会产生较小的迭代误差,此时算法接近收敛,且下一次迭代的步长和核宽度减小,以保证算法的稳定性和鲁棒性,直至权系数达到最优解,算法完全收敛.因此,AKLMS算法相比KLMS算法和LMS算法在收敛速度和预测精度方面应有所提升,后面实验也会进行验证.
2 卫星网络流量预测在卫星网络系统中,系统能量供给、计算资源和存储资源都十分有限,因此实际可行的卫星网络流量动态预测算法必须在收敛、预测精度以及复杂度方面同时具有极高的性能.否则很难适应环境复杂的卫星网络系统.
AKLMS算法以LMS算法为基础,利用高斯核函数将数据向高维空间映射,使ALMS算法在再生核希尔伯特空间内完成.它在权系数迭代过程中使用了MCC准则,提高了算法的鲁棒性能,而且自适应地根据瞬时误差大小及时地调整步长和核宽度,提高了算法的收敛性能和预测精度,并能保证算法的稳定性. AKLMS算法和LMS算法一样,具有较低的算法复杂度. AKLMS算法所具有的性能优势能满足卫星网络对流量预测的苛刻要求. AKLMS卫星网络流量预测的具体步骤如下.
步骤1 输入卫星节点流量样本数据x={x1, x2, x3, …, xn},并确保样本长度;
步骤2 参数设置:形状控制参数α,范围控制参数β,基准核宽度σ,滤波器长度δ,初始化权系数w0,预设迭代误差阈值ε;
步骤3 权系数迭代.根据i时刻之前的流量值迭代出第i+1时刻最优权系数.通过AKLMS算法进行权系数迭代,当迭代误差小于ε时终止迭代,并输出最优权系数w*={wj|ej≤ε},j∈{1, 2, …, n};
步骤4 计算并得到i+1时刻流量的预测值
目前无法采集到卫星网络流量的真实数据.但Liu等[8]证明了卫星网络流量与地面网络流量一样具有自相似性,而且根据卫星网络的信道传输特性分析了卫星网络流量的特点,并使用和分析了某地面骨干网的网络流量数据集[15],证明可以用该组数据模拟卫星网络流量来建立预测模型.因此,使用此数据集作为模拟卫星网络流量的仿真对象.为了方便处理数据,首先对数据进行归一化化处理:
| $ {x_i} = \frac{{{x_i} - \min \left( {{x_i}} \right)}}{{\max \left( {{x_i}} \right) - \min \left( {{x_i}} \right)}} $ | (8) |
选择不同的参数会对AKLMS算法产生不同的影响,下面以平均误差(AE,average error)作为评价标准,在不同的参数下对AKLMS算法进行误差分析,并以此作为参数选择的标准.在σ=0.5、β=2的情况下,不同α值的预测误差如表 1所示,当α=1.0时平均误差最小.在α=1.0、σ=0.5的情况下,不同β值的预测误差如表 2所示,当β=2时平均误差最小.在α=1.0、β=2的情况下,不同σ值的预测误差如表 3所示,当σ=0.5时平均误差最小. AKLMS算法的步长是由参数α、β和en通过式(6)计算得到,故不在此讨论步长的选择.
|
|
表 1 不同α值的平均误差 |
|
|
表 2 不同β值的平均误差 |
|
|
表 3 不同σ值的平均误差 |
收敛性能是评价算法优劣的一个非常重要的标准.在仿真过程中,考虑到算法收敛曲线的稳定性,设置固定步长μ=0.02、核宽度基准σ=0.5、自适应步长形状控制参数α=1、自适应步长范围控制参数β=2.在上述参数相同的情况下得出不同算法的收敛速度如图 1所示.由于核函数的作用,KLMS算法的收敛速度明显比LMS算法快.由于AKLMS算法能同时自适应地调整步长和核宽度,其收敛速度也明显优于KLMS算法.同时,还将AKLMS算法与其子算法步长自适应KLMS(S-AKLMS, step length-adaptive kernel LMS)和子算法核宽度自适应KLMS(K-AKLMS, kernel width-adaptive kernel LMS)相比较,AKLMS算法的收敛性能明显优于两种子算法.可以看到,步长自适应是算法收敛性能提升的主要原因.核宽度自适应不仅在一定程度上提升了算法的收敛性能,它还保证了算法的稳定性.
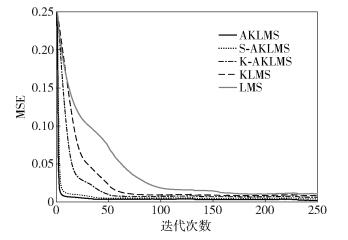
|
图 1 不同算法收敛性能比较 |
为了更直观地显示网络流量预测的效果,将3种算法的预测结果与真实值相比较,如图 2所示,AKLMS算法预测结果比KLMS和LMS算法预测结果更接近真实值. 3种算法的误差如图 3所示,采用真实值和预测值的绝对误差对预测误差进行评价,从图 3中可以直观地看出,AKLMS算法的预测误差比KLMS和LMS算法的预测误差小很多.
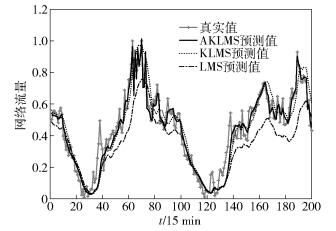
|
图 2 预测结果比较 |

|
图 3 预测误差比较 |
预测误差的累积分布曲线如图 4所示,AKLMS算法的预测误差小于0.1的概率为91.54%,小于0.05的概率为63.68%. KLMS算法的预测误差小于0.1的概率为73.13%,小于0.05的概率为36.82%. LMS算法的预测误差小于0.1的概率为49.75%,小于0.05的概率为25.37%.其中预测误差小于0.1的概率,AKLMS算法相比KLMS算法提升了18.41%,相比LMS算法提升了41.79%.预测误差小于0.05的概率,AKLMS算法相比KLMS算法提升了26.86%,相比LMS算法提升了38.31%.通过以上数据分析,充分证明了AKLMS算法比KLMS和LMS算法的预测精度更高.
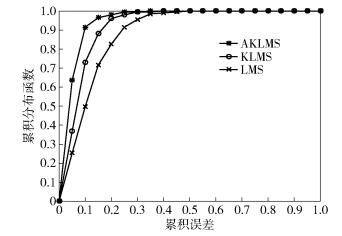
|
图 4 误差的累积分布曲线 |
提出了一种自适应步长和自适应核宽度的核最小均方算法(AKLMS),针对卫星网络流量的特性,以经典LMS算法为基础,结合核函数与MCC准则,能够自适应地调整步长和核宽度,使其在收敛性能和预测精度方面都明显优于同类算法.算法复杂度低,能更好地适应卫星网络的复杂环境,为卫星网络的流量规划、路由设计以及网络检测提供了可靠的基础.由于没有考虑流量的测量噪声,而且只进行了一步预测仿真,下一步将继续完善该算法,将此算法应用到卫星网络的路由设计中.
| [1] | Gamvros I, Raghavan S. Multi-period traffic routing in satellite networks[J]. European Journal of Operational Research, 2012, 219(3): 738–750. doi: 10.1016/j.ejor.2011.11.004 |
| [2] | Gao Zihe, Guo Qing, Na Zhenyu. A distributed routing algorithm with traffic prediction in LEO satellite networks[J]. Information Technology Journal, 2011, 10(2): 285–292. doi: 10.3923/itj.2011.285.292 |
| [3] | Yan Dong, Wang Luyuan. TPDR: traffic prediction based dynamic routing for LEO&GEO satellite networks[C]//International Conference on Electronics Information and Emergency Communication. Beijing: IEEE, 2015: 104-107. |
| [4] | Qu Hua, Ma Wentao, Zhao Jihong, et al. Prediction method for network traffic based on maximum correntropy criterion[J]. China Communications, 2013, 10(1): 134–145. doi: 10.1109/CC.2013.6457536 |
| [5] | Ma Wentao, Qu Hua, Zhao Jihong. Estimator with forgetting factor of correntropy and recursive algorithm for traffic network prediction[C]//2013 25th Chinese on Control and Decision Conference (CCDC). Guiyang: IEEE, 2013: 490-494. |
| [6] |
秦红祥, 杨飞. 一种新的卫星通信网流量预测算法[J]. 电讯技术, 2013, 53(7): 835–839.
Qin Hongxiang, Yang Fei. A new traffic flow prediction algorithm for satellite network[J]. Telecommunication Engineering, 2013, 53(7): 835–839. doi: 10.3969/j.issn.1001-893x.2013.07.002 |
| [7] | 杜巍. 卫星互联网自相似业务预测方法的研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014083960.htm |
| [8] | Liu Weifei, Pokharel P P, Principe J C. The kernel least-mean-square algorithm[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 543–554. doi: 10.1109/TSP.2007.907881 |
| [9] | Zhao Jihong, Wang Tao, Ma Wentao, et al. The kernel-LMS based network traffic prediction[C]//IET International Conference on Information Science and Control Engineering. Shenzhen: IET, 2012: 62-66. |
| [10] | Liu Xi, Qu Hua, Zhao Jihong, et al. Maximum correntropy unscented Kalman filter for spacecraft relative state estimation[J]. Sensors, 2016, 16(9): 1530. doi: 10.3390/s16091530 |
| [11] | Chen Badong, Xing Lei, Zhao Haiquan, et al. Generalized correntropy for robust adaptive filtering[J]. IEEE Transactions on Signal Processing, 2016, 64(13): 3376–3387. doi: 10.1109/TSP.2016.2539127 |
| [12] | Liu Xi, Qu Hua, Zhao Jihong, et al. State space maximum correntropy filter[J]. Signal Processing, 2017(130): 152–158. |
| [13] | Wang Weihua, Zhao Jihong, Qu Hua, et al. Convergence performance analysis of an adaptive kernel width MCC algorithm[J]. AEU-International Journal of Electronics and Communications, 2017(76): 71–76. |
| [14] |
覃景繁, 欧阳景正. 一种新的变步长LMS自适应滤波算法[J]. 数据采集与处理, 1997(3): 171–174.
Qin Jingfan, Ouyang Jingzheng. A novel variable step size LMS adaptive filtering algorithm based on sigmoid function[J]. Journal of Data Acquisition & Processing, 1997(3): 171–174. |
| [15] | 150 Megabit Ethernet anonymized packet traces without payload: WIDE-TRANSIT link[DB/OL]. (2009-04-03)[2017-07-06]. http://mawi.wide.ad.jp/mawi/ditl/ditl2009/. |


