针对EGBIS分割算法中的过分割问题,提出了一种基于超像素的graph-based图像分割算法SGBIS.首先,对图像进行基于简单线性迭代聚类(SLIC)的超像素预分割;然后以每个超像素作为节点构造带权无向图,以相邻超像素颜色平均值的欧式距离作为图中边的权值;最后利用基于图的算法合并超像素得到分割结果.用Ⅵ、PRI和F值3个指标分析了算法性能,结果表明,新算法可以得到更为理想的分割效果;引入交互分割区域合并,也可满足用户图像分割的需求.
As graph-based algorithm is inclined to over-segment, a new graph-based image segmentation algorithm based on superpixels called superpixel graph based image segmentation (SGBIS) was proposed and simple linear iterative clustering (SLIC) superpixels segmentation was employed as pre-segmentation. Then, the weighted undirected graph regarding superpixels as nodes was constructed, the Euclidean distance of adjacent superpixels' average color is used as the weight. Finally, the segmentation results are obtained by merging superpixels based on graph-based algorithm. Three indexes variation of information (Ⅵ), probabilistic rand index (PRI) and F-measure are introduced to evaluate algorithm. Experiments show that it can get better segmentations. An interactive region merging interface is also introduced, which could meet users need very well.
图像分割是图像处理的重要研究内容. Felzenswalb和Huttenlocher[1]提出的EGBIS(efficient graph-based image segmentation)算法将图模型与区域合并方法结合,得到自适应阈值的快速分割,能获取更多空间上的非局部特性,且算法结构和实现简单,因此被广泛应用.但该算法存在过分割问题.笔者结合EGBIS算法和SLIC(simple linear iterative clustering)超像素[2],用超像素替代像素构建图模型,得到较为理想分割结果,显著减少了过分割现象.
1 相关工作按照是否需要人的参与,图像分割可分为交互式分割和非交互式分割.交互式分割算法通过在图像中标记种子点来给出分割先验信息,从而有效分割出目标物体和前背景等.经典的交互式分割算法有图割算法[3]和随机游走分割[4]算法等,前者把图像的前景背景分割问题建模为图的最小割问题,后者则通过未知节点游走到种子节点概率进行标记,大量算法在此基础上进行改进[5-7].对于非交互的(无监督的)图像分割,常用的有基于聚类的方法[8]和以Markov随机场[9]为代表的统计方法,以及水平集方法[10]等.
EGBIS算法是一种常用的无监督分割算法. Mo J[11]为解决EGBIS算法过分割的问题,首先使用Mean Shift对图像进行平滑,然后从RGB色彩空间转化到Lab色彩空间构建图模型,同时改进EGBIS算法的权重函数. Chen Z H等[12]以3×3区域为单位对图片进行下采样,减少了像素间颜色的差异,然后把3×3区域视为节点构造图,不仅减少边的数目加速了算法,而且改善了过分割的情况. Ming Zhang[13]考虑预期分割数目,若分割块数多于预期数,新定义的阈值函数将倾向于合并像素.与文献[14]中首先将图像的像素聚类成可视块的思想类似,本文则从用超像素代替像素的思路出发,改进了EGBIS算法的过分割问题.
2 SGBIS图像分割算法 2.1 EGBIS算法EGBIS算法是基于图的贪心聚类算法,假定G=(V, E)为无向图,点集vi∈V表示待分割的像素集,边(vi, vj)∈E对应图像的相邻像素对.每条边的权重w((vi, vj))表示由边连接的两个像素vi和vj的非相似性度量.分割过程就是将V划分为若干部分,每个部分对应结果图G′=(V, E′)中的一个连通区域,其中E′∈E.通常,分割趋于使一个区域内的元素相似,不同区域内的元素不相似.这表明连接一个区域内两点的边权重相对较低,连接不同区域内两点的边权重较高.
2.2 SLIC超像素SLIC算法是由Achanta等[2]提出的基于K均值聚类的超像素分割算法.算法首先在图像上均匀选择多个聚类中心,然后对每个像素,计算与它一定距离内的聚类中心的相似度,相似度计算考虑颜色相似度和距离远近,把该像素划分为最相似的聚类中心,然后更新聚类中心并重复上述步骤,直到聚类中心不再有明显变化.
2.3 SGBIS算法为了解决EGBIS算法容易过分割的问题,笔者结合SLIC超像素和EGBIS算法提出SGBIS(superpixel graph based image segmentation)算法.假定生成N个SLIC超像素区域Ri.在Sgb0基础上构造图G=(S, E, W),其中S表示超像素集,E表示边集,W表示边的权重.对每个超像素,分别计算内部3个颜色通道的平均值作为其颜色特征,如图 1所示.图 1(a)表示SLIC超像素预分割的结果,图 1(b)表示对应的以平均颜色描述的特征图.以图 1(b)左上角的超像素为例,它包含了221个像素,它的3个通道的平均值分别为r′=135, g′=159, b′=50.
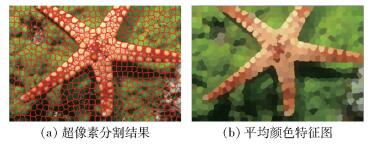
|
图 1 SLIC超像素与特征图 |
计算边集E中每个边的权重W,权重由2个相邻超像素颜色均值的欧式距离表示.
| $ w\left( e \right) = \sqrt {{{\left( {{{r'}_1} - {{r'}_2}} \right)}^2} + {{\left( {{{g'}_1} - {{g'}_2}} \right)}^2} + {{\left( {{{b'}_1} - {{b'}_2}} \right)}^2}} $ | (1) |
将边集E按权重值非降序排列,依次判断连接边的2个区域是否满足合并条件.初始条件下,1个超像素代表 1个区域,定义类内差异为区域内最小生成树的最大权重.
| $ {\rm{Int}}\left( {{R_i}} \right) = \mathop {\max }\limits_{e \in {\rm{MST}}\left( {{R_i},E} \right)} w\left( e \right) $ | (2) |
|
|
表 1 18张实验图片分割结果对比 |
其中MST(Ri, E)表示边集组成的最小生成树.
2个区域
| $ {\rm{Dif}}\left( {{R_1},{R_2}} \right) = \mathop {\max }\limits_{{s_i} \in {R_1},{s_j} \in {R_2},\left( {{s_i},{s_j}} \right) \in E} w\left( {{s_i},{s_j}} \right) $ | (3) |
区域是否合并的标准定义为
| $ D\left( {{R_1},{R_2}} \right) = \left\{ \begin{array}{l} {\rm{true}},\;\;\;\;\;\;{\rm{Dif}}\left( {{R_1},{R_2}} \right) < {\rm{MInt}}\left( {{R_1},{R_2}} \right)\\ false,\;\;\;\;\;{\rm{Dif}}\left( {{R_1},{R_2}} \right) \ge {\rm{MInt}}\left( {{R_1},{R_2}} \right) \end{array} \right. $ | (4) |
其中最小类内差异MInt(R1, R2)定义为
| $ \begin{array}{*{20}{c}} {{\rm{MInt}}\left( {{R_1},{R_2}} \right) = }\\ {\min \left\{ {{\rm{Int}}\left( {{R_1}} \right) + \tau \left( {{R_1}} \right),{\rm{Int}}\left( {{R_2}} \right) + \tau \left( {{R_2}} \right)} \right\}} \end{array} $ | (5) |
Int(R1)和Int(R2)分别是区域R1和R2能容忍的最大差异.当所有边遍历结束后,分割完成. τ(Ri)为阈值函数:
| $ \tau \left( {{R_i}} \right) = k/\left| {{R_i}} \right| $ | (6) |
其中|Ri|表示区域Ri所包含的像素数,k是某个常数. τ(Ri)为小区域设定一个范围,使相邻小区域差别较大时也可合并.随着区域增大,|Ri|变大,τ(Ri)越来越小,其作用忽略不计. k为阈值参数,若k=0,导致过分割; 若k→∞,整幅图片会聚为一个区域.因此,随着k值增大,分割后的图片区域增大.
3 检测方法为了客观地评价分割结果,以人工分割结果Sg为参照,使用区域评价标准Ⅵ(variation of information)[15]、PRI(probabilistic rand index)[16]和边界评价标准F值3个指标对算法分割结果Stest进行评估,指标原理如下.
Ⅵ表示一个分割相对于另一个分割的平均条件熵:
| $ {\rm{VI}}\left( {{S_{{\rm{test}}}},{S_{\rm{g}}}} \right) = H\left( {{S_{{\rm{test}}}}\left| {{S_{\rm{g}}}} \right.} \right) + H\left( {{S_{\rm{g}}}\left| {{S_{{\rm{test}}}}} \right.} \right) $ | (7) |
Ⅵ越小,Stest相对于Sg的信息变化越小,Stest越接近Sg.如果2个分割完全相同,那么Ⅵ为0.
PRI从统计学的角度定义分割的准确性. 2个分割的PRI参数定义为
| $ {\rm{PRI}}\left( {{S_{{\rm{test}}}},{S_{\rm{g}}}} \right) = \frac{1}{{C_N^2}}\sum {\left[ {{I_{ij}}{p_{ij}} + \left( {1 - {I_{ij}}} \right)\left( {1 - {p_{ij}}} \right)} \right]} $ | (8) |
其中Pij表示像素对在Sg和Stest中标记一致的概率. PRI值越大,说明Stest与Sg越接近.
边界评价标准F值比较算法分割和人工标记得到的边界,公式如下:
| $ F = \frac{{2PR}}{{P + R}} $ | (9) |
P为查准率,表示算法得到的边界属于人工标记边界的概率,R为查全率,表示人工标记边界被检测到的概率. Stest与Sg分割越接近,F值越高.
1组Sg计算指标的方式为:对于1张图的每个Stest,分别与所有Sg计算指标,取平均值并记录,遍历所有Stest后以使该平均值最高的Stest得到的平均指标作为该幅图的评价结果.
4 仿真实验 4.1 算法步骤SGBIS算法步骤如下.
输入:彩色图像
输出:分割结果Sgb
第1步 指定N个超像素,得到SLIC超像素预分割结果Sgb0=(R1, …, RN).
第2步 以超像素为节点构建图模型,计算每个超像素与其相邻超像素的不相似度作为边的权值.
第3步 根据边的权值构建图的最小生成树,将树中的边按权重值非降序排列得到e1, e2, …, en;
第4步 对于q=1, …, n,重复步骤5.
第5步 在分割Sgbq-1的基础上构建egb:设si和sj是eq两端的区域,即eq=(si, sj),且
第6步 返回分割结果Sgb=Sgbn.
SGBIS算法的具体过程如图 2所示.
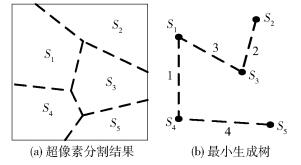
|
图 2 超像素分割与最小生成树构建 |
图 2(a)所示为超像素分割结果,共5个超像素S1~S5,其面积分别为7、8、5、4、2.
图 2(b)所示为对应图模型的最小生成树.按照边的非降序排列为
| $ {S_1}{S_4} \to {S_2}{S_3} \to {S_1}{S_3} \to {S_4}{S_5} $ | (10) |
算法第5步的过程如图 3所示.按照排序,第1步判断S1和S4是否合并,假设参数k=20,根据公式计算类间差异和最小类内差异为
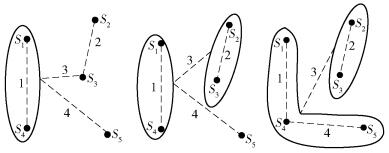
|
图 3 区域合并过程 |
第2步判断S2和S3,同理可以计算得Dif(S2, S3)=1 < MInt(S2, S3)=2.5,故S2和S3合并.
第3步判断合并后的区域(S1, S4)与(S2, S3)是否合并,计算可得Dif(S2, S3)=3>MInt(S2, S3)=2.8,故两区域不合并.
第4步判断(S1, S4)与S5是否合并,计算可得Dif(S2, S3)=4 < MInt(S2, S3)=10,故两区域合并.
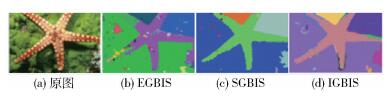
4.2 实验结果实验平台为Visual Studio 2013,如图 4所示.选取Berkeley数据集BSD500的18张图进行实验. BSD500数据集每张图像包含由粗到细多张人工分割结果.对于每张图片,分别使用EGBIS算法和SGBIS算法,同时使用文献[11]中的IGBIS(improved graph-based image segmentation)算法作为对比.图 5所示为3种算法在其中1张图像上的分割结果.为了满足用户的分割需求,算法分割完成后,可点选区域进行合并,如图 6所示.
|
图 4 实验平台 |
|
图 5 不同算法分割结果示例 |

|
图 6 人工选点区域合并改善分割结果 |
如图 5所示,提出的SGBIS算法和IGBIS算法[11]都可以有效减少过分割的小区域,但是IGBIS算法在图像中物体的边界上产生了额外的过分割区域,其根本原因在于:虽然IGBIS算法使用了Mean Shift平滑,并增加了额外的超参数,但都是对图像整体进行平滑,在减小了物体内部差异度的同时使边界变得模糊.而所提出的SGBIS算法有效解决了这个问题,它对每个超像素求平均,是1种局部平滑方法,边界信息得以有效保存,因此不会在边界附近产生过分割区域.
如表 1所示,SGBIS算法在3个指标上均优于EGBIS和IGBIS算法.总体上,SGBIS算法相比于EGBIS算法,改进了其易过分割的缺点,对于自然图像的主体分割结果更加完整、理想.但是正因为改进算法更倾向于合并像素,可能丢失背景的一些细节,将背景分割为一个整体.与IGBIS算法比较,SGBIS算法的分割结果边缘更为平滑,性能更好.
5 结束语在计算机视觉领域,图像分割算法一直受到广泛的关注,笔者针对EGBIS算法易于过分割的问题,在构造无向图前,先对原图进行预分割,得到形状大小基本一致且贴合图像边界的SLIC超像素;然后以超像素的颜色平均值对其进行特征描述,视其为节点构造无向权重图,进而实现基于图的无监督分割.
通过主观评价和客观评价对文献[1]和文献[11]的算法在BSDS500数据集上进行了对比实验.从图示和指标结果来看,改进算法能得到相对完整的分割结果,较好地解决了EGBIS算法过分割的问题.今后可以结合更好的超像素分割算法,以使性能进一步提升.
| [1] | Felzenszwalb P F, Huttenlocher D P. Efficient graph-based image segmentation[J]. International Journal of Computer Vision, 2004, 59(2): 167–181. doi: 10.1023/B:VISI.0000022288.19776.77 |
| [2] | Achanta R, Shaji A, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274–2282. doi: 10.1109/TPAMI.2012.120 |
| [3] | Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222–1239. doi: 10.1109/34.969114 |
| [4] | Grady L. Random walks for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(11): 1768–1783. doi: 10.1109/TPAMI.2006.233 |
| [5] | Bampis C G, Maragos P, Bovik A C. Graph-driven diffusion and random walk schemes for image segmentation[J]. IEEE Transactions on Image Processing, 2017, 26(1): 35–50. doi: 10.1109/TIP.2016.2621663 |
| [6] |
依玉峰, 高立群, 郭丽. 基于Mean Shift随机游走图像分割算法[J]. 计算机辅助设计与图形学学报, 2011, 23(11): 1875–1878, 1881.
Yi Yufeng, Gao Liqun, Guo Li. Mean shift based random walker interactive image segmentation[J]. Journal of Computer-Aided Design & Computer Graphics, 2011, 23(11): 1875–1878, 1881. |
| [7] | Dong X, Shen J, Shao L, et al. Sub-Markov random walk for image segmentation[J]. IEEE Transactions on Image Processing, 2016, 25(2): 516–527. doi: 10.1109/TIP.2015.2505184 |
| [8] |
纪则轩, 潘瑜, 陈强, 等. 无监督模糊C均值聚类自然图像分割算法[J]. 中国图像图形学报, 2011, 16(5): 773–783.
Ji Zexuan, Pan Yu, Chen Qiang, et al. Natural image segmentation algorithm with unsupervised FCM[J]. Journal of Image and Graphics, 2011, 16(5): 773–783. |
| [9] | Tu Z, Zhu S C. Image segmentation by data-driven Markov chain Monte Carlo[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 657–673. doi: 10.1109/34.1000239 |
| [10] |
杨辉华, 赵玲玲, 潘细朋, 等. 基于水平集和凹点区域检测的粘连细胞分割方法[J]. 北京邮电大学学报, 2016, 39(6): 11–16.
Yang Huihua, Zhao Lingling, Pan Xipeng, et al. Overlapping cell segmentation based on level set and concave area detection[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(6): 11–16. |
| [11] | Mo J, Wang C, Zhang T, et al. Improved graph-based image segmentation based on mean shift 1[C]//Proceedings of International Conference on Communications and Networking in China (CHINACOM). Guilin: IEEE Computer Society Press, 2013: 685-689. |
| [12] | Chen Z H, Xiao X L, Liu Y, et al. Graph-based imagesegmentation with bag-of-pixels[C]//Proceedings of International Conference on Machine Learning and Cybernetics. Tianjin: IEEE Computer Society Press, 2013: 1548-1551. |
| [13] | Zhang M, Alhajj R. Improving the graph-based image segmentation method[C]//Proceedings of International Conference on Tools with Artificial Intelligence. Arlington: IEEE Computer Society Press, 2006: 617-624. |
| [14] |
冯筠, 刘飞鸿, 李盼, 等. 基于格式塔认知框架的腹腔CT多目标分割算法[J]. 北京邮电大学学报, 2016, 39(5): 51–55.
Feng Jun, Liu Feihong, Li Pan, et al. Multi-object segmentation for abdominal CT Images based on gestalt cognitive framework[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(5): 51–55. |
| [15] | Meilǎ M. Comparing clusterings: an axiomatic view[C]//Proceedings of the International Conference on Machine Learning. Bonn: ACM, 2005: 577-584. |
| [16] | Unnikrishnan R, Pantofaru C, Hebert M. Toward objective evaluation of image segmentation algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(6): 929–944. doi: 10.1109/TPAMI.2007.1046 |


