2. 国网冀北电力有限公司 信息通信分公司, 北京 100053
针对当前电力数据网风险预警模型无法有效预测网络风险的现状,提出一种基于熵权-灰色模型的电力数据网风险预测机制,重点解决网络整体风险的预测问题.首先利用灰色模型对电力数据网的风险指标进行预测,确定单项风险指标值;然后采用熵权法得出每一项指标的动态权重;最后根据风险指标值和权重得出网络整体的预测风险值.仿真验证结果表明,该模型可保证动态网络下实时预测的准确度.
2. State Grid Jibei Electric Power Company Limited Information & Communication Dispatch, Beijing 100053, China
Aiming at the present situation that risk prediction model of power data network cannot effectively predict the risk, a risk prediction mechanism of power data network based on entropy weight-gray model is proposed. This paper focuses on risk prediction of the entire network. Firstly, the gray model is used to predict the risk indexes of power data network, and the individual risk index value is determined. Then, the dynamic weight of each index is obtained by entropy weight method. Finally, it can calculate the risk value of the network according to the risk index value and the weight. The simulation results show that the proposed model can guarantee predictive accuracy of dynamic real-time network.
随着智能电网的快速建设, 电力数据网的应用日益广泛.电力数据网包括电力调度数据网和电力综合数据网,承载着电力企业的生产信息、管理信息、业务信息等,日益开放的网络环境给系统的安全运行带来新的挑战.提高电力数据网的可靠性不能仅依靠网络设计阶段的优化,更要在网络运行过程中,通过有效的风险预测,发现潜在风险.传统的网络风险处理机制大多是在故障发生之后进行应急处理,一方面由于复杂的网络结构使得故障的识别定位困难导致故障处理不及时;另一方面应急处理只能被动应对已发生风险,而对风险已经造成的损失无法弥补.由于电力数据网承载的业务对网络可靠性要求高,网络的时效性和安全性等关键性能必须予以保障,因此针对电力数据网的风险预测研究具有重要意义.
提出一种基于熵权-灰色模型的电力数据网风险预测机制,首先利用灰色模型预测影响风险的多个网络风险指标值,然后结合熵权法计算出风险指标权重,最后提出风险评估模型实现对网络未来风险的有效评估.
1 相关工作目前在智能电网运维研究中,对网络整体风险评估和预警的研究较少,主要是针对单个业务进行风险分析,Gupta S等[1]对智能电网的断电风险进行了分析,采用比较2个数据样本之间K-L散度的方法衡量当前数据的异常程度,并通过与由历史经验得出的KLD阈值比较决定是否发出告警,该方法可以预测断电风险及时阻止电网的未来大规模停电,但只是比较了两个样本的散度,并不适用网络整体风险的预测告警. Zhang Yu等[2-3]结合风险识别和风险评估,构建了多层次、多指标的风险指标体系,但是Zhang Yu等[2]只针对电力负荷过载这单一风险进行分析和预警, 而Gu等[3]只考虑天气影响.近年来,随着机器学习的兴起,Hafeez等[4]提出了基于神经网络的电网风险预测方法,人工神经网络可以应用于分析非精确性规律、关系复杂的样本数据,有较高的数据预测准确度,但需要大量的历史数据和足够多的训练次数,且神经网络参数的设定需要不断调试,具有局部最优,泛化能力差,实时性不高等问题. Li等[5]使用粗糙集预处理检测数据,提取关键分量作为神经网络的输入数据,提高了神经网络的收敛速度和近似精度.熊飞[6]选取了多个网络资源指标, 提出了一种基于藤Copula-GARCH模型的预测方法, 并采用贝叶斯网络对网络风险展开了适当的评估,实现了对网络资源的有效预测,但是仍无法解决算法复杂度高泛化能力不强的问题.
针对这一问题,卢懿等研究将灰色预测模型引入风险预测中,灰色预测模型是灰色系统理论的重要应用之一,适用于“小样本,贫信息”的不确定性系统的预测[7-8].灰色预测原理简单,性能优良,目前在电网相关的应用还只局限于对电量负荷的预测. Li等[9]证明灰色模型在电网负荷预测中具有优越性;Ding等[10]利用马尔可夫模型对基于灰色神经网络的光伏系统发电预测模型进行改进,预测结果适用于多种典型天气下的发电预测.
目前针对电力数据网风险预测的研究较少[11-12],且电力数据网风险预测的重点是对网络整体风险的预测,因此将结合电力数据网特性,采用灰色预测理论对网络整体风险进行预测.
此外,现有的风险预测都是将历史风险值作为训练数据进行建模预测,仅考虑在过去网络环境影响下风险的发展趋势,没有将现在及未来时刻网络的可能运行环境作为考虑因素.如亓峰[6, 13]等提出了电网的整体风险预测模型,但针对风险预测的建模都是将量化后的风险值作为依据,复杂处理过的风险值信息损失严重且不能体现网络当前运行状态,预测效果无法令人满意.因此,将对影响网络风险的多因素风险指标进行预测,从而在风险预测中体现当前网络运行状态对风险的影响.
另一方面,由于风险指标间的关系复杂且不断变化,如何围绕风险指标体系设计出合理的风险评估模型直接影响预测风险值准确性.提出一种基于熵权法的指标权重确定方法,首先对风险指标进行无量纲化生成,接着依据动态熵值客观地确定指标权重,为多指标风险评估模型提供有效依据.
综上,主要贡献包括:1)充分考虑未来网络运行环境对风险的影响,提出基于灰色模型(GM)的网络运行多指标预测模型,该模型计算简单且模型参数具有动态性,提高了风险预测精度;2)提出基于熵权的风险指标权重计算方法,先对指标无量纲化生成,然后利用指标值的信息熵来确定多指标权重分配问题,评价完全依赖于实际问题域,杜绝了主观随意性.
2 基于熵权-灰色模型的风险预测传统的网络风险管理重点放在应对已发生风险,而对风险造成的损失无法弥补.由于电力数据网承载的业务对可靠性和时效性要求更高,为了防患于未然实现有效的网络安全保障,需要能够准确快速的发现潜在风险,在事故发生前发出告警.针对电力数据网提出基于熵权-灰色模型的风险预测机制,首先利用灰色预测构建网络的多指标预测模型,得出各风险指标预测值;然后提出熵权算法对各风险指标进行权重分析,实现了多指标值的无量纲化和权重生成;最后提出风险评估方法对风险进行评估,给出衡量网络整体风险的指标值,并对风险级别进行判定,作为风险告警的依据.
2.1 灰色预测模型GM(1, 1)的基本形式灰色预测模型是基于时间序列的,通过构造累加数列对多指标数据进行有效处理,可增强预测的实时性和对病态数据的抗干扰性.预测模型构造步骤如下:
1) 生成累加矩阵
假设共有m项影响网络的风险指标,每项指标采样n个时刻,x(i)(j)表示第i项指标第j个时刻的采样指标值,令
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{X^{\left( 1 \right)}}\left( 1 \right)}&{{X^{\left( 1 \right)}}\left( 2 \right)}& \cdots &{{X^{\left( 1 \right)}}\left( n \right)}\\ {{X^{\left( 2 \right)}}\left( 1 \right)}&{{X^{\left( 2 \right)}}\left( 2 \right)}& \cdots &{{X^{\left( 2 \right)}}\left( n \right)}\\ \cdots&\cdots&\cdots&\cdots \\ {{X^{\left( m \right)}}\left( 1 \right)}&{{X^{\left( m \right)}}\left( 2 \right)}& \cdots &{{X^{\left( m \right)}}\left( n \right)} \end{array}} \right] $ | (1) |
2) 构造灰色差分方程并求解
GM(1, 1)预测模型的原始形式如下:
| $ {x^{\left( i \right)}}\left( k \right) + a{X^{\left( i \right)}}\left( k \right) = b $ | (2) |
则称下式为灰色差分方程:
| $ {x^{\left( i \right)}}\left( k \right) + a{Z^{\left( i \right)}}\left( k \right) = b $ | (3) |
其中:
| $ \hat A = \left( {\begin{array}{*{20}{c}} {\hat a}\\ {\hat b} \end{array}} \right) = {\left( {{B^T}B} \right)^{ - 1}}{B^T}{Y_n} $ | (4) |
其中均值生成B与常数项向量Yn分别为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{2}\left( {{X^{\left( i \right)}}\left( 1 \right) + {X^{\left( i \right)}}\left( 2 \right)} \right)}&1\\ { - \frac{1}{2}\left( {{X^{\left( i \right)}}\left( 2 \right) + {X^{\left( i \right)}}\left( 3 \right)} \right)}&1\\ \cdots&\cdots \\ { - \frac{1}{2}\left( {{X^{\left( i \right)}}\left( {n - 1} \right) + {X^{\left( i \right)}}\left( n \right)} \right)}&1 \end{array}} \right]}\\ {{Y_n} = \left[ {\begin{array}{*{20}{c}} {{x^{\left( i \right)}}\left( 2 \right)}\\ {{x^{\left( i \right)}}\left( 3 \right)}\\ \cdots \\ {{x^{\left( i \right)}}\left( n \right)} \end{array}} \right]} \end{array} $ | (5) |
将解出的
| $ {X^{\left( i \right)}}\left( {\hat k + 1} \right) = \left( {{X^{\left( i \right)}}\left( 1 \right) - \frac{{\hat b}}{{\hat a}}} \right){e^{ - \hat ak}} + \frac{{\hat b}}{{\hat a}},k = 1,2, \cdots ,n $ | (6) |
累减还原得到待预测数据的估计值:
| $ \begin{array}{*{20}{c}} {{x^{\left( i \right)}}\left( {\hat k + 1} \right) = {X^{\left( i \right)}}\left( {\hat k + 1} \right) - {X^{\left( i \right)}}\left( {\hat k} \right) = }\\ {\left( {1 - {e^{\hat a}}} \right)\left( {{x^{\left( i \right)}}\left( 1 \right) - \frac{{\hat b}}{{\hat a}}} \right){e^{ - \hat ak}},k = 2,3, \cdots ,n} \end{array} $ | (7) |
在实际建模中,为了进一步降低病态数据对预测精度的影响,原始数据序列中的数据不一定全部用来建模.我们可以通过在原始数据序列中取出一部分数据,来建立一个模型.一般来说,取不同的数据,建立的模型也不一样.
定义1 用
定义2 用
定义3 置入最新信息x(0)(n+1),替换最老信息x(0)(1),称用
从预测的角度看,一般来说,新陈代谢模型是最理想的.随着系统的发展,老数据对系统当前状态的刻画作用越来越差,在不断产生新信息的同时,及时地去掉老信息能够更加贴合当前系统的运行状况.此外,不断地进行新陈代谢,可以避免因信息增加带来的数据量的扩大.
综合考虑以上,采取新陈代谢GM(1, 1)进行电力数据网风险指标的多指标值预测.假设数据网有m项风险指标,时间序列取前n个时刻, 则算法的时间复杂度为O(2×m×n), 是多项式级的,效率上可满足电力数据网风险预测的实时性要求.
2.3 基于熵权法的风险评估1) 指标无量纲化
由于指标量纲不同,在进行风险评估建模时难以直接进行指标间的计算分析,因而首先需要对风险指标矩阵进行无量纲化以消除不同量纲的不可比性.不同的无量纲化方法会影响熵权法的效果,采用性能最优的极值处理法[14],并将量化结果控制在[0, 100]上.
按照指标属性可将指标分为正相关型(取值越大,风险越高)、负相关型(取值越大,风险越小)、0—1型(指标只有对立的两种情况)和模糊型指标(只可用语言描述,如服务质量好、一般、差等)4类.根据指标分类,分别通过下式进行无量纲化处理:
正相关型指标:
| $ {\lambda _k} = \frac{{x\left( k \right) - \mathop {\min }\limits_k \left\{ {x\left( k \right)} \right\}}}{{\mathop {\max }\limits_k \left\{ {x\left( k \right)} \right\} - \mathop {\min }\limits_k \left\{ {x\left( k \right)} \right\}}} \times 100,k = 1,2, \cdots ,n $ | (8) |
负相关型指标:
| $ {\lambda _k} = \frac{{\mathop {\max }\limits_k \left\{ {x\left( k \right)} \right\} - x\left( k \right)}}{{\mathop {\max }\limits_k \left\{ {x\left( k \right)} \right\} - \mathop {\min }\limits_k \left\{ {x\left( k \right)} \right\}}} \times 100,k = 1,2, \cdots ,n $ | (9) |
0-1型指标:由于指标只有对立两种情况,所以根据实际情况取值0或100.
模糊型指标:通过专家评价将其去模糊化,转化为0~100之间的清晰数值.
2) 熵权法确定权重
风险评估时,当某一指标在各评估对象中的差异较大时,说明其包含的信息量多、对评估系统的分辨能力强,应当给其赋予较大的权重.采用熵权法对指标权重赋值.
风险指标矩阵为
| $ {p_{ij}} = \frac{{{x^{\left( i \right)}}\left( j \right)}}{{\sum\limits_{j = 1}^n {{x^{\left( i \right)}}\left( j \right)} }} $ | (10) |
计算第i项指标的熵值:
| $ {e_i} = \frac{1}{{\ln n}}\sum\limits_{j = 1}^n {{p_{ij}}\ln \frac{1}{{{p_{ij}}}}} $ | (11) |
第i项指标的差异性系数为
| $ {g_i} = 1 - {e_i} $ | (12) |
则第i项指标的指标权重为
| $ {\omega _i} = \frac{{{g_i}}}{{\sum\limits_{i = 1}^m {{g_i}} }} $ | (13) |
由上述步骤得到网络风险指标的各项权重,权重的确定摆脱了主观不确定性影响,符合网络风险评估的需要.
通过2.2节可以得到每一项网络风险指标的预测指标值,用λi表示第i项风险指标预测值.通过2.3节得到每一项网络风险指标的权重,用ωi表示为第i项指标的权重.
2.4 网络风险判别得到了网络各个风险指标的预测值和权重,下面需要对网络整体的风险情况进行评价.网络整体的风险情况可主要从两个方面衡量,一方面是网络风险值;另一方面是网络风险离散程度,分别由下式计算:
| $ {R_N} = \sum\limits_{i = 1}^m {\left( {{\lambda _i}{\omega _i}} \right)} $ | (14) |
| $ {V_N} = \frac{1}{{{R_N}}}\sqrt {\sum\limits_{i = 1}^m {\left[ {{\omega _i} \times {{\left( {{\lambda _i} - {R_N}} \right)}^2}} \right]} } $ | (15) |
其中:RN为网络风险值,VN为网络风险离散程度,λi为第i项指标风险值,ωi为第i项指标的权重.网络风险值是描述网络整体风险的平均值,网络风险值大,表示网络肯定存在至少一种风险.网络风险离散程度是一个相对值,各指标风险值分布越离散,网络风险离散程度越大,说明网络运行情况不合理,会带来网络风险.综合这两个指标给出网络风险等级,从而实现对网络风险的判别.网络风险等级与风险值、风险离散程度的对应关系如表 1所示.其中,区间(βi, βi+1]和(ηi, ηi+1)分别表示RN和VN对应风险等级的取值范围,具体数值根据网络实际情况给出.
|
|
表 1 网络风险等级与风险值、风险离散程度关系 |
电力数据网覆盖范围广泛,网络结构复杂,实际环境中能对网络产生风险的因素非常多.参考已有指标体系,依据全面性和科学性原则,选取三类共20个指标进行仿真实验,具体指标如表 2所示.
|
|
表 2 风险指标选取及分类 |
实验数据根据某网省电力数据网2016年的实际运行情况确定.选取神经网络方法、固定权重方法和直接使用网络风险值进行预测的方法和所提的熵权-灰色预测方法进行对比,实验采用Matlab(2016b)进行仿真.
3.2 实验结果与分析为了对所建模型的预测性能进行客观评价和比较,以平均相对误差A(MRE, mean relative error)、均方根误差B(RMSE, root mean square error)和平均绝对误差C(MAE, mean absolute error)来衡量算法预测的准确性.
| $ A = \frac{1}{S}\sum\limits_{l = 1}^S {\left| {\frac{{\left( {R_N^l - R_N^{l'}} \right)}}{{R_N^l}}} \right| \times 100\% } $ | (16) |
| $ B = \sqrt {\frac{{\sum\limits_{l = 1}^S {{{\left( {R_N^l - R_N^{l'}} \right)}^2}} }}{S}} $ | (17) |
| $ C = \frac{1}{S}\sum\limits_{l = 1}^S {\left| {R_N^l - R_N^{l'}} \right|} $ | (18) |
其中: S为实验样本数,RNl为第l个样本的网络实际风险值,RNl′为第l个样本的网络预测风险值.
图 1所示为根据网络各指标实测值,通过风险评估得到的网络风险值与灰色预测风险值的比较.可以看出,在网络风险逐渐变大的过程中,熵权-灰色预测的拟合值可以快速的跟上变化趋势,能够实现在风险尚未造成故障时的及时告警.
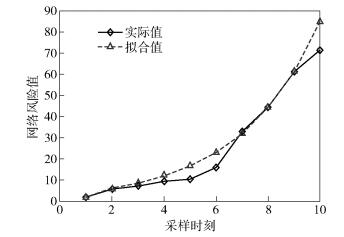
|
图 1 算法拟合效果 |
图 2所示为所提的熵权-灰色模型与神经网络方法、固定权重方法和直接使用网络风险值预测方法的预测准确度对比结果.表 3所示为各预测方法的误差分析.
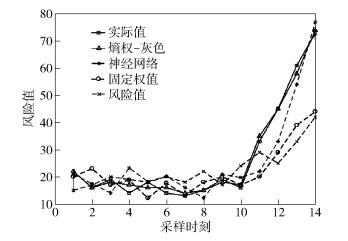
|
图 2 各算法预测结果对比 |
|
|
表 3 各算法误差结果对比 |
由图 2和表 3可知,在前期网络安全运行时,各种预测方法的误差都不大,但是熵权-灰色预测的结果误差率最低;当网络出现问题风险快速上升时,各对比方法精确度大幅下降.直接使用网络风险值进行预测的方法性能最差,有时甚至产生与网络实际风险相反的变化趋势,这是因为网络整体风险值是经过复杂处理后的信息,损失较大,且没有考虑当前的网络运行状态,用它作为预测依据已不适用当下网络环境.采用固定指标权重的方法,在网络风险动态变化时反应较差,这是因为没有考虑随着网络动态变化,不同风险指标对网络风险的影响权重也会动态变化.采用BP神经网络进行预测的预测精度较优但对风险的反映速度明显低于熵权-灰色预测,这是因为在动态性强的网络中,可利用的历史数据有限,神经网络无法达到足够的训练次数,泛化能力不足.而熵权-灰色模型每次只考虑待预测时刻前的少量数据,在保证准确性的同时,算法的时间空间复杂度都远低于神经网络.
以上是对网络风险值的比较,为了进行更准确的风险等级判别,还需要将网络离散程度考虑进来,如图 3所示.

|
图 3 判别结果对比 |
由图 3可知,在网络安全运行时,只考虑网络风险值(判决结果Ⅰ)与综合考虑网络风险值和网络风险离散程度(判决结果Ⅱ)进行风险判别的结果一致.但是当网络因某项风险因素而风险增大时,两者产生分歧,判决结果Ⅱ可以更早地发出更高级别的风险告警.这是因为网络风险值仅可以衡量网络整体风险水平,是体现网络平均风险水平的指标;而网络风险离散程度描述各风险指标值分布的离散程度,可以将因某一风险指标过大导致的网络风险识别出来.通过这两个指标从不同角度对网络风险进行评价能更及时全面地反映网络实际运行的风险情况.
综上所述,可以认为熵权-灰色模型对历史数据有限,有较强动态性的电力数据网的风险预测具有更好的性能.
4 结束语为了解决电力数据网风险预测的问题,提出基于熵权-灰色模型的风险预测机制.通过使用基于时间序列的灰色预测模型,保证网络动态变化下风险预测的准确性的同时,简化了预测的时间和空间复杂度,适合对实时性要求高的网络的风险预测.另一方面,提出基于熵权法的指标动态评估,将权重的分配完全依赖于客观问题域,更好地适应动态网络和复杂环境下不同风险指标影响程度的变化.最后在风险判别阶段综合考虑网络风险值和网络离散程度给出更合理的告警.
所进行的风险预测与评估都是默认风险指标相对独立,然而在实际环境中,诱发网络风险的因素通常会有所关联,要考虑各种指标之间的相对关系.通过关联分析,更加准确的评估网络风险,这将是作者的下一步方向.
| [1] | Gupta S, Waghmare S, Kazi F, et al. Blackout risk analysis in Smart grid WAMPAC system using KL divergence approach[C]//International Conference on Power Systems. New Delhi: IEEE, 2016: 1-6. http://ieeexplore.ieee.org/document/7584069/ |
| [2] | Zhang Yu, Zhang Tianshu, Song Xiaohui, et al. Research on risk warning system of distribution network[C]//International Conference on Power System Technology. Chengdu: IEEE, 2014: 1509-1514. http://ieeexplore.ieee.org/document/6993787/ |
| [3] | Gu T, Janssen J, Tazelaar E, et al. Risk prediction in distribution networks based on the relation between weather and (underground) component failure[C]//CIRED-Open Access Proceedings Journal. Glasgow: IEEE, 2017: 1442-1445. |
| [4] | Hafeez K, Khan S. Risk management analysis with the help of lightning strike mapping around 500 k-v grid station using artificial intelligence technique[C]//International Conference of Robotics and Artificial Intelligence. Nanjing: IEEE, 2012: 165-168. |
| [5] | Li Jinying, Zhao Yuzhi, Li Jinchao. Power grid safety evaluation based on rough set neural network[C]//International Conference on Risk Management & Engineering Management. Chongqing: IEEE Computer Society, 2008: 245-249. |
| [6] | 熊飞. 基于Copula理论的网络资源风险预测研究[D]. 武汉: 湖北工业大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10500-1017815836.htm |
| [7] | 卢懿. 灰色预测模型的研究及其应用[D]. 杭州: 浙江理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10338-1014229928.htm |
| [8] | Li Zeyuan, Shang Yunlong, Cui Naxin, et al. The prediction method for battery open circuit voltage based on GM (1, 1) grey model[C]//Chinese Control Conference (CCC). Hangzhou: IEEE, 2015: 1902-1906. |
| [9] | Li Xiaobing, Jing Zhaoxia, Wu Qinhong. Application of improved GM(1, N) models in annual electricity demand forecasting[C]//Innovative Smart Grid Technologies-Asia. Washington: IEEE, 2015: 1-6. |
| [10] | Ding Kun, Feng Li, Wang Xiang, et al. Forecast of PV power generation based on residual correction of Markov chain[C]//International Conference on Control, Automation and Information Sciences. Changshu: IEEE, 2015: 355-359. http://ieeexplore.ieee.org/document/7338692/ |
| [11] | Li Meng, Li Wenjing, Yu Peng, et al. Risk prediction of the SCADA communication network based on entropy-gray model[C]//International Conference on Network and Service Management (CNSM). Tokyo: IEEE, 2017: 1-5. https://www.computer.org/csdl/proceedings/cnsm/2017/98/00/08256004-abs.html |
| [12] | Li Meng, Li Wenjing, Zeng Xiangjian, et al. A decision-making mechanism of network risk control based on grey relation[C]//IEEE/IFIP Network Operations and Management Symposium (NOMS). Taipei: IEEE, 2018: 1-4. |
| [13] |
亓峰, 李琪, 韩骞, 等. 基于神经网络的电力通信网风险评估方法[J]. 北京邮电大学学报, 2014, 37(1): 90–93.
Qi Feng, Li Qi, Han Qian, et al. Risk assessment method of power communication network based on neural network[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(1): 90–93. |
| [14] |
朱喜安, 魏国栋. 熵值法中无量纲化方法优良标准的探讨[J]. 统计与决策, 2015(2): 12–15.
Zhu Xian, Wei Guodong. Discussion on the standard of non-dimensional method in entropy method[J]. Statistic and Decision, 2015(2): 12–15. |


