针对机械臂工作场景复杂、任务需求多样的特点,提出了一种基于改进图规划的机械臂任务规划方法.首先建立针对机械臂任务规划的通用数学表征模型;其次结合机械臂的任务特性与改进模拟退火算法,提出一种基于图规划的改进任务规划算法,将传统算法单一的规划结果拓展为任务动作序列集合;最后,基于该集合求解融合不同目标的机械臂任务执行策略,并以七自由度机械臂为仿真对象对该方法的正确性和有效性进行了验证.结果表明,与传统规划方式相比,提出的方法具备优先考虑不同目标任务执行策略的能力,同时可以有效缩短规划时间.
In order to deal with the complex work scene and diverse task demands of manipulator task, a manipulator task planning method based on improved graph planning is proposed. Firstly a common mathematical model of manipulator task planning is established, and then combined with the task characteristics of manipulator and the improved simulated annealing algorithm, an improved task planning algorithm based on graph planning is proposed, which extends the single planning result of traditional algorithm to the set of task action sequences. Finally, the task execution strategy is solved by fusion of different targets. A simulation of 7-degree of freedom manipulator verifies the correctness and effectiveness of the proposed method. The results show that compared with the traditional task planning algorithm, the proposed method has the ability to prioritize tasks with different targets and can shorten plan time.
近年来,机械臂技术已经广泛应用于工业装配、深空探测、服务业等领域,随着机械臂技术在各个领域应用的深入,机械臂的工作场景日趋复杂.机械臂在完成任务的过程中,需要兼顾关节行程、末端距离、灵活性及能量等多种因素.因此,依靠人为设定机械臂动作序列的传统方法已经很难兼顾纷繁复杂的任务目标,进而,需要引入机械臂的任务规划方法,代替操作者完成复杂繁重的计算任务.
针对机器人任务规划技术,国内外学者已经开展了相关问题的研究.在任务规划发展初期,Fikes[1]为描述机器人任务执行过程,提出了STRIPS格式语言实现机器人基本动作的组合,规划结果为由初始状态到目标状态的行动序列.在STRIPS语言的基础上,McDermott[2]提出了PDDL格式语言,该语言能够对领域内对象的初始状态、目标、动作等规划元素进行形式化描述,形成一种通用的描述机制.为了更好地描述任务规划过程,Blum等[3]提出了图规划方法,该方法首次利用图结构描述任务规划问题,将STRIPS型问题转变为通过搜索可以解决的规划问题,使任务规划领域有了新的突破.图规划算法具有简洁、易于描述、可拓展性强的优点.但是,图规划是一种非启发式搜索算法,所以面对复杂问题,其规划效率不高.为了提高任务规划效率,李等[4]在图规划过程中引入马尔可夫决策过程,利用概率的方法进行任务规划,该方法虽然提高了图规划效率,但规划过程存在丢弃解的情况.刘等[5]提出了一种混沌蚁群算法提高多机器人协同任务规划效率,但该方法只能得到唯一解.余等[6]提出一种交互式仿生群协进化混合规划算法,该算法虽然具备收敛速度快的优点,但是缺乏针对不同任务目标的优化能力.对于大规模、过于复杂应用场景,一些学者提出了层次任务网(HTN, hierarchical task network)规划[7],HTN规划将目标状态用抽象的目标任务替代,任务按照不同的抽象程度形成分层结构,极大程度地减小了规划过程的复杂度.但是,由于HTN任务规划描述方法过于复杂,任务分层方法不唯一,不同分层方式规划结果差别较大,所以,很难有效评估其规划结果的优劣.
通过调研,现有的任务规划方法大部分着眼于对复杂规划过程的求解及规划效率的提高,缺乏对于不同任务执行策略的对比及优选过程.考虑图规划作为搜索规划方法,具备可拓展性强的特点,以图规划算法为基础,开展机械臂任务规划方法的研究.
1 任务规划数学模型建立下面通过建立任务状态、动作的数学表征模型,描述机械臂的任务规划过程.
1.1 任务状态描述任务状态是指任务规划过程中某一时刻机械臂及环境的状态信息.定义状态矩阵S描述任务状态,形式为

|
(1) |
其中:矩阵TS为利用DH参数法[8]构建的描述机械臂末端位姿的4×4的齐次变换矩阵;矩阵WS为描述环境状态的矩阵,形式为

|
(2) |
其中:
假设环境中存在p个可操作物,操作物具有q种可能状态,则有
| $ n = \max \left\{ {p,q} \right\} $ | (3) |
为保证矩阵WS*的齐次性,以零行或零列补齐矩阵.
1.2 任务动作描述任务动作为机械臂的可执行动作.定义动作矩阵A描述任务动作,形式如下
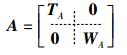
|
(4) |
其中:TA为描述机械臂末端坐标系的平移、旋转变化的4×4的齐次矩阵;WA为描述环境中操作物状态变化的矩阵,可以分解为
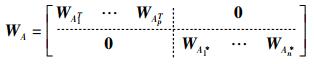
|
(5) |
其中:WAiT为描述环境中物体平移、旋转的4×4的齐次矩阵,表示第i个物体状态变化的n×n的齐次矩阵,可以通过对角阵I的初等列变换得到.
1.3 规划过程描述通过状态矩阵与动作矩阵的相互作用,可以实现任务执行过程的描述.设任务规划的第k-1步的状态矩阵为Sk-1,动作矩阵为Ak-1,相乘可得
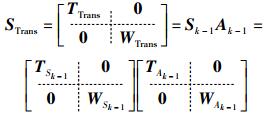
|
(6) |
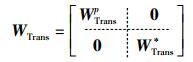
其中:STrans为执行动作后机械臂的状态转移矩阵;WTrans为描述环境的状态转移矩阵,通过分块矩阵相乘得到,可以由下述分块矩阵表示
|
(7) |
其中WTransp、WTrans*为经过动作矩阵作用的n行4×n列、n行n×n列的矩阵.
可以通过状态转移矩阵提取当前的状态矩阵,则第k步的状态矩阵Sk的元素可以表示为
| $ \left. \begin{array}{l} {\left( {{\mathit{\boldsymbol{T}}_{{S_k}}}} \right)_{ij}} = {\left( {{\mathit{\boldsymbol{T}}_{{\rm{Trans}}}}} \right)_{ij}},i,j = 0,1,2,3\\ {\left( {{\mathit{\boldsymbol{W}}_{{S_k}}}} \right)_{ij}} = {\left( {\mathit{\boldsymbol{W}}_{{\rm{Trans}}}^p} \right)_{ij * }},i = 0,1, \cdots ,p;j = 0,1,2,3\\ {\left( {{\mathit{\boldsymbol{W}}_{{S_k}}}} \right)_{\left( {i + p} \right)j}} = {\left( {\mathit{\boldsymbol{W}}_{{\rm{Trans}}}^ * } \right)_{i{j^\mathit{\dagger }}}},i,j = 0,1, \cdots ,n\\ {j^ * } = \left( {i \times 4} \right) + j\\ {j^\mathit{\dagger }} = \left( {i \times n} \right) + j \end{array} \right\} $ | (8) |
通过上述数学模型的建立,实现了针对不同机械臂与环境的任务规划过程描述,为任务执行过程的求解奠定了基础.
2 基于改进图规划的任务动作序列求解图规划分为图拓展与规划解提取2个阶段,下面通过改进图拓展过程,将单一任务规划结果拓展为任务动作序列集合.
2.1 考虑机械臂任务特性的分层图规划为实现图规划过程,选取移动、抓取、释放等典型机械臂动作构建任务动作集合,并设定每个动作的前提条件、添加效果与删除效果.通过添加或删除动作执行效果可以实现任务在不同状态之间的转移.在图拓展过程中,状态节点和动作节点交替出现,直到所有期望状态出现在同一状态层为止.
针对操作环境中存在一台机械臂及多个物体的典型机械臂操作任务,考虑图规划特性,为避免图拓展过程的不必要搜索,以任务目标状态为起始时间步的状态,逆向构建由目标状态出发搜索任务初始状态的规划图,并结合机械臂特性与图规划特点,采用动作分层方式规划,在图拓展阶段只考虑动作执行顺序,在规划解提取阶段考虑具体动作规划算法,以此提高图规划算法性能.
2.2 基于改进模拟退火算法的图拓展传统图规划算法在期望状态出现时,搜索过程即停止,可获得动作最少的规划解.但在任务规划过程中,针对不同任务目标,动作数最少的解不一定为任务最优解.所以,在图规划过程中引入改进的模拟退火算法,当图拓展到达期望状态后,规划以一定的概率继续拓展.
2.3 基于模拟退火算法的图拓展模拟退火算法来源于将固体加热后冷却的退火过程.通过模拟退火算法可赋予搜索过程一种时变且最终趋于零的概率突跳性.
通过结合图拓展与模拟退火算法,使规划图在当前时间步出现初始状态时继续拓展,搜索最少动作数规划结果以外的规划解.当规划图未达到任一初始状态时,图拓展被看作使内能增加过程,状态总是向着下一步转移,则有
| $ {\mathit{\boldsymbol{S}}_i} \to {\mathit{\boldsymbol{S}}_{i + 1}} $ | (9) |
当规划图到达过初始状态后,图拓展被看作内能减小过程,规划图以一定的概率继续拓展,并且概率随着时间步的推移逐渐降低,表示为
| $ P\left( {{\rm{d}}E} \right) = \exp \left( {\frac{{{\rm{d}}E}}{{k\mathit{\boldsymbol{T}}}}} \right) $ | (10) |
其中:dE为转移的能量差,T为当前温度,k为比例系数.由于是退火过程,所以dE < 0,温度T越高,状态转移概率P(dE)越大.
2.4 改进模拟退火算法基于模拟退火算法的改进图拓展可以在原有规划结果的基础上继续搜索.但是,图拓展步数过多,会在一定程度上降低图规划效率,并且针对不同任务,过多的拓展可能出现较多重复动作的无意义规划解.基于此,在模拟退火算法中引入信息熵,动态改变模拟退火算法的温度衰减系数,使模拟退火算法可以更好地适应图规划过程.图拓展过程中当前时间步状态的信息熵定义为
| $ {\rm{Ent}}\left( t \right) = - \sum\limits_{k = 1} {{y_k}{\rm{lb}}{y_k}} ,\;\;\;k = 0,1 $ | (11) |
其中:pk表示时间步t中第k类状态所占比例,k=0代表在之前任一时间步中出现过的状态,k=1代表未在之前任一时间步中出现过的状态.
信息熵的取值在0~1之间,信息熵的值越小,代表当前时间步的状态的“纯度”越高.如果当前时间步中大部分状态为已经达到过的状态,图拓展为无意义的循环过程;如果当前时间步中大部分状态为未达到过的状态,规划图达到稳定状态所需步数过多,造成规划时间过长,并且规划结果大概率不满足任务需求.因此,当状态纯度高时,需要温度加快衰减,加速图规划过程.所以,将每一时间步的信息熵作为退火过程中温度的衰减系数为
| $ \left. \begin{array}{l} {r_t} = {\rm{Ent}}\left( t \right)\\ T_{t + 1}^r = {r_t}{T_t} \end{array} \right\} $ | (12) |
其中:rt表示温度衰减系数,Tr表示模拟退火算法在时间步t时的温度,Tt+1r表示基于信息熵求出的时间步t+1的温度.
通常情况下,为保证模拟退火算法的稳定性,其温度下降速度应不快于
| $ T_t^{\min } = {T_0}/\left( {1 + \ln \left( {t - {t_0} + 1} \right)} \right) $ | (13) |
其中:Ttmin表示算法在时间步t的最低温度,T0为模拟退火算法的初始温度,t0表示第一次搜索达到初始状态所用步数.则改进模拟退火算法的温度衰减过程可以表示为
| $ {T_{t + 1}} = \max \left\{ {T_{t + 1}^r,T_{t + 1}^{\min }} \right\} $ | (14) |
通过改进正向图拓展,在兼顾规划效率的基础上进一步拓展搜索结果为任务动作序列的集合.在此基础上,可以实现考虑不同目标的任务规划解提取.
3 多目标融合的任务规划解提取在改进图拓展结果基础上,基于具体动作规划算法,可以求解针对不同目标的最优动作执行策略.
基于典型图规划算法提取任务规划解,在提取过程中,根据机械臂具备的规划算法,进行具体化选择,如针对移动任务,机械臂通常具备笛卡儿空间直线、样条曲线规划及关节空间规划等一种或多种规划方式.在选择过程中,基于不同任务需求,需要考虑相应任务指标,如关节行程、末端距离、能量消耗等.通过设定相应的权重值,融合不同任务目标,提取任务规划解.提取过程中第k步动作代价可由下式计算
| $ {f_k}\left( p \right) = {\omega _1}{f_1}\left( p \right) + {\omega _2}{f_2}\left( p \right) + \cdots + {\omega _i}{f_i}\left( p \right) + \cdots $ | (15) |
其中:fi为根据具体规划算法设计的针对不同任务目标的计算或估值函数,ωi为相应目标的代价权重值,p表示规划过程中的决策变量,如关节角、末端位置姿态等.
通过上述过程,由改进图拓展结果的不同状态层中的初始状态向前搜索,可以求得任务规划解集,根据式(16)选择任务最优规划解.
| $ \min \left\{ {\sum\limits_{k = 1} {f_k^{\left( 1 \right)}\left( x \right)} ,\sum\limits_{k = 1} {f_k^{\left( 2 \right)}\left( x \right)} , \cdots ,\sum\limits_{k = 1} {f_k^{\left( n \right)}\left( x \right)} \cdots } \right\} $ | (16) |
在每一步动作选择过程中,通过设置不同目标的权值提取任务规划解,可以得到考虑多目标的机械臂任务执行策略的Pareto解集.
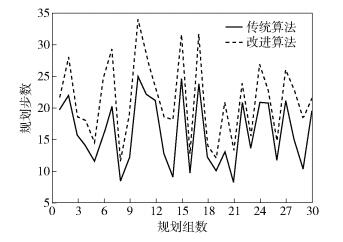
4 仿真校验 4.1 改进图拓展性能分析通过对比传统图规划与提出的改进图规划的规划结果,验证提出的改进方法的优越性.设定机械臂可以执行抓取、移动、释放动作.根据不同的机械臂初始构型及操作物体数量、位置,规划30组机械臂移动操作物的任务,得到如图 1~图 3所示结果.通过仿真,提出的改进算法在传统图规划算法的基础上,拓展了规划步数,保证规划结果不少于5组任务动作序列.同时,通过以目标为导向的动作分层规划,减少不低于10%的任务规划时间,有效提升了算法效率.
|
图 1 改进任务规划算法规划步数对比 |

|
图 2 改进任务规划算法动作序列数 |
|
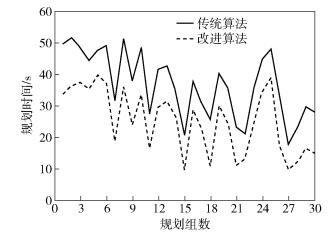
图 3 改进任务规划算法规划时间对比 |
以机械臂移动过程中的关节行程及末端距离作为指标衡量规划解提取过程中针对不同目标的优选规划解的能力,以机械臂的关节角及末端位置作为决策变量,任务目标可以由下式计算
| $ \left. \begin{array}{l} {f_1}\left( {{p_1},{p_2}} \right) = \sum\limits_{i = 1}^7 {\left| {{q_{2,i}} - {q_{1,i}}} \right|} \\ {f_1}\left( {{p_1},{p_2}} \right) = \sum\limits_{i = 1}^3 {\left| {{x_{2,i}} - {x_{1,i}}} \right|_2^2} \end{array} \right\} $ | (17) |
其中:q1, i与x1, i为机械臂初始关节角与末端位置,q2, i与x2, i为机械臂期望关节角与末端位置.
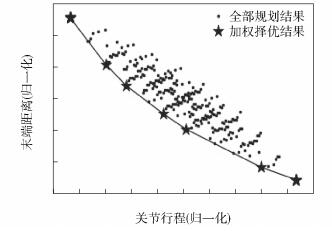
机械臂具备笛卡儿空间直线规划及关节空间规划的能力,根据任务动作序列中各中间点的坐标,在保证关节1角度不变的情况下,位置级逆解各任务中间点的构型.在空间中分别设置9组可操作物,并设置各操作物的目标状态.在考虑任务目标的情况下,生成满足约束的所有任务执行过程,分别得到各执行过程的关节行程与末端距离,采用目标加权融合方法通过设置不同的目标权值,优选动作执行过程,得到如图 4所示的结果.
|
图 4 多目标融合规划结果 |
通过上述结果可知,在改进图拓展的基础上,通过融合不同目标,提取任务规划解,可以得到考虑多目标的非劣任务执行策略.
5 结束语提出一种针对机械臂任务规划的通用数学表征方法,能够实现对任意的机械臂任务规划过程的数学描述.基于动作分层思想改进图规划,提高规划效率,并通过基于信息熵的改进模拟退火算法,有效地增加了图拓展的步数,生成任务动作序列的集合.在此基础上,通过融合不同目标,提取任务规划解,实现了考虑多目标的任务执行策略优选过程.
| [1] | Fikes R E, Nilsson N J. STRIPS: a new approach to the application of theorem proving to problem solving[C]//Computation & intelligence. American Association for Artificial Intelligence, 1995: 189-208. http: //www. sciencedirect. com/science/article/pii/0004370271900105 |
| [2] | Helmert M. Concise finite-domain representations for PDDL planning tasks[J]. Artificial Intelligence, 2009, 173(5): 503–535. |
| [3] | Blum A L, Furst M L. Fast planning through planning graph analysis[J]. Artificial Intelligence, 1997, 90(1-2): 281–300. doi: 10.1016/S0004-3702(96)00047-1 |
| [4] |
李月光, 尹东, 张荣. 一种导览机器人的任务规划方法研究[J]. 计算机工程, 2014, 40(3): 196–200.
Li Yueguang, Yi Dong, Zhang Rong. Study on a task planning method for tour guide robot[J]. Computer Engineering, 2014, 40(3): 196–200. doi: 10.3969/j.issn.1000-3428.2014.03.041 |
| [5] |
刘晓莹, 蔡自兴, 余伶俐, 等. 一种正交混沌蚁群算法在群机器人任务规划中的应用研究[J]. 小型微型计算机系统, 2010, 31(1): 164–168.
Liu Xiaoying, Cai Zixing, Yu Lingli, et al. An orthogonal-cluster chaos ant colony algorithm based on swarm-robots system mission planning application research[J]. Journal of Chinese Computer Systems, 2010, 31(1): 164–168. |
| [6] |
余伶俐, 蔡自兴. 基于异质交互式文化混合算法的机器人探测任务规划[J]. 机器人, 2009, 31(2): 137–145.
Yu Lingli, Cai Zixing. Robot detection mission planning based on heterogeneous interactive cultural hybrid algorithm[J]. Robot, 2009, 31(2): 137–145. doi: 10.3321/j.issn:1002-0446.2009.02.007 |
| [7] | Erol K, Hendler J, Nau D S. UMCP:a sound and complete procedure for hierarchical task-network planning[J]. Aips, 1994: 249–254. |
| [8] | Ben-Gharbia K M, Maciejewski A A, Roberts R G. Modifying the kinematic structure of an anthropomorphic arm to improve fault tolerance[C]//International Conference on Robotics and Automation. Seattle: IEEE Press, 2015: 1455-1460. http: //ieeexplore. ieee. org/document/7139381/ |


