2. 中国科学院大学 材料科学与光电技术学院, 北京 100049;
3. 中国科学院大学 电子电气与通信工程学院, 北京 100049
针对透明光网络交叉连接过程中交叉点易受干扰的问题,提出了耦合干扰的研究方法,模拟了合法信号和干扰源耦合的工作方式,分析了不同信号传输速率、不同干扰功率比耦合方式下干扰源对合法信号的影响,并量化了通信系统传输信号的质量.对此方法进行多次光网络通信系统实验验证后的结果表明,该方法有助于检查光网络通信系统是否存在干扰源,并可有效预防干扰源对合法信号的干扰.
2. College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
A coupling interference method was proposed to research the problem of interference occurring with optical cross-connects in the transparent optical network. To quantify the signal quality of the communication system, the operational model was simulated and the influences of interfering source on the legal signal with different traffic rates, interfering power ratio were analyzed based on this method. Multiple verification experiments were established and the experimental results shows that this method are helpful for testing the existence of interfering source and preventing the influence of interfering source on legal signal in the transparent optical network.
光传输网络大多采用波分复用技术,该技术广泛应用于共享工作空间、多方实时多媒体通信、电子服务等领域[1].这些应用加快了全球通信流量的发展,将带来光交叉器件数量的爆炸性增长[2].同时,由于激光的准直性好,很难被侦听的特性,激光通信被广泛应用在国防安全和军事信息传递中.但是,光网络交叉点非常容易受到干扰[3],如激光干扰[4-6]、非线性噪声[7]、光接收器配置[8]、多芯光纤的有限隔离[9]、不完美的光滤波器件[10]等信号干扰因素都会使系统通信质量降低,从而使光网络无法正常传输信号.目前,在研究信号干扰造成通信系统质量下降的问题中,Rebola等[11]提出用矩母函数来估计直接检波正交频分复用的性能,这种方法复杂且并未考虑恶意干扰情况下的信号质量问题. Oliveira等[12-13]测试了各种先进的调制格式,其结果表明,采用越先进的调制格式,测试系统的耐受性越差,但由于非相干光通信和相干光通信是两套系统,高阶调制下的相干光通信系统无法表征直调直探方式下的信号变化. Rejeb[14]提出的MALI算法能够为信号干扰所引起的故障管理提供帮助,这种算法使用大量光器件做硬件实现,结构复杂,实现难度大.因此,目前并没有一种简单可靠的干扰信号源测量方法,用以量化干扰源对信号质量的影响.针对以上问题,提出了一种简单的耦合干扰实验,以50/50耦合器作为干扰光学器件,研究光交叉点中的信号干扰问题.
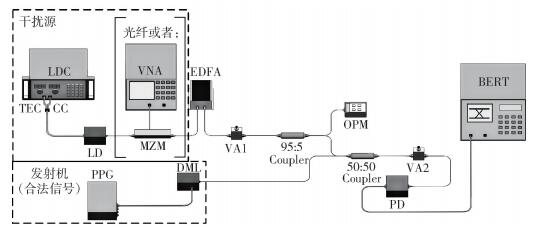
1 光信号耦合干扰法在透明光网络系统信号传输过程中,通常采用强度调制和直接探测的方法传输信号,其通信链路由发射机和光电探测器(PD,photo-detector)所构成(见图 1).其中,发射机包括码型发生器(PPG,programme pulse generator)和直接调制激光器(DML,direct modulation laser). PPG产生伪随机码,通过直调激光器将信号加载到光载波上,由此产生合法光信号.光信号经过光网络传输后,由PD直接探测,并转换成电信号,最后由误码分析仪(BERT,bit error rate tester)分析电信号,计算误码率,以此评估系统信道质量.
|
图 1 实验演示系统原理图 LDC:激光控制器;TEC:热电冷却器;CC:电流控制器;LD:激光器;MZM:马曾调制器;EDFA:掺铒光纤放大器;VA:可变衰减器;OPM:光功率计. |
在透明光网络传输系统中,通过耦合注入的方式模拟光交叉点上发生的信号干扰.该方法通过改变干扰源波长,使其与合法信号光波长相近,利用耦合器将干扰信号耦合进合法信道中,使干扰源淹没合法信号,最终实现对合法信号传输干扰,如图 1所示.
1.2 信噪比与误码率合法信号通常采用二进制启闭键控(OOK,on-off key)调制格式传输大信号,并用误码率表示光网络中信号的传输能力,误码率的公式为[15]
| $ B = p\left( 1 \right)p\left( {0\left| 1 \right.} \right) + p\left( 0 \right)p\left( {1\left| 0 \right.} \right) $ | (1) |
其中p(1)和p(0)分别表示可能出现“1”和“0”信号的概率.由伪随机码基本特性可知,其序列中出现“1” “0”码型的数量是一致的,因此p(1)=p(0)=1/2. p(0|1)和p(1|0)分别表示传输“1”和“0”信号时出现的误码概率,可表示为
| $ p\left( {0\left| 1 \right.} \right) = \frac{1}{2}{\rm{erfc}}\left( {\frac{{{I_1} - {I_{\rm{D}}}}}{{\sqrt 2 {\sigma _1}}}} \right) $ | (2) |
| $ p\left( {1\left| 0 \right.} \right) = \frac{1}{2}{\rm{erfc}}\left( {\frac{{{I_{\rm{D}}} - {I_{\rm{0}}}}}{{\sqrt 2 {\sigma _0}}}} \right) $ | (3) |
其中:I1和I0分别表示信号为“1”和“0”时的光电流,σ1, 0是I1, 0的高斯概率密度函数中的变量,ID是误码仪判断“1”“0”信号的阈值光电流,通常取σ1=σ0=σ,ID=(I1+I0)/2,则误码率的公式为
| $ B = \frac{1}{2}{\rm{erfc}}\left( {\frac{{{I_1} - {I_0}}}{{\sqrt 2 \left( {{\sigma _1} + {\sigma _0}} \right)}}} \right) = \frac{1}{2}{\rm{erfc}}\left( {\frac{{{I_1}}}{{2\sqrt 2 \sigma }}} \right) $ | (4) |
考虑到透明光网络中并不引入电噪声,因此在接收端光电探测器(p-i-n)中,信噪比(SNR,signal-noise ratio)可以表示为[16-17]
| $ S = \frac{{{I^2}}}{{{\sigma ^2}}} = \frac{{I{'}_1^2 + I{'}_0^2}}{{2{\sigma ^2}}} $ | (5) |
但在引入耦合干扰后,由于干扰源的加入,使得干扰后进入PD的光功率提高,PD判决光电流提高,有效电信号被淹没,出现“0”电平的概率升高,出现“1”电平的概率降低.可令
| $ B = \frac{1}{2}{\rm{erfc}}\left( {\frac{{{I_1} + {I_{\rm{i}}}}}{{2\sqrt 2 \sigma }}} \right) = \frac{1}{2}{\rm{erfc}}\left( {\frac{{{I_1}}}{{\sqrt 2 \sigma }}} \right) $ | (6) |
| $ S\left( I \right) = \frac{{I_1^2{{\left( {1 - k\left( I \right)} \right)}^2}}}{{2{\sigma ^2}}} $ | (7) |
其中Ii为干扰源光电流,约等于I1,同时,SNR可以写成与PD自身性能相关的公式:
| $ S = \frac{{{I^2}}}{{{\sigma ^2}}} = \frac{{{R^2}I_{{\rm{in}}}^2}}{{\sigma _{\rm{s}}^2 + \sigma _{\rm{T}}^2}} $ | (8) |
其中:R为PD响应度;Iin为PD的平均输入光电流;σs为散粒噪声,σT为热噪声,σs和σT可分别表示为
| $ \sigma _{\rm{s}}^2 = 2q\left( {R{I_{{\rm{in}}}} + {I_{\rm{d}}}} \right)\Delta f $ | (9) |
| $ \sigma _{\rm{T}}^2 = 4\left( {\frac{{{K_B}T}}{L}} \right){F_n}\Delta f $ | (10) |
其中:q为电子常数,Id为暗电流,Δf为接收机带宽,T为温度,L为阻抗,Fn为放大倍数.式中响应度R和Δf都是与系统的传输速率相关的变量.则将PD参数代入式(8)~式(10)可算出温度为27℃,PD接收功率为-12.05dBm时,S=25.44dB.经过耦合干扰后,若PD接收功率保持不变,则SNR会降低到18dB左右.
将式(6)~(8)合并,可以得到误码率与信噪比之间的关系为
| $ \begin{array}{*{20}{c}} {B\left( I \right) = \frac{1}{2}{\rm{erfc}}\left( {\sqrt S \left( {1 - k\left( I \right)} \right)} \right) = }\\ {\frac{1}{2}{\rm{erfc}}\left( {\frac{{R{I_{{\rm{in}}}}\left( {1 - k\left( I \right)} \right)}}{{\sqrt {\sigma _{\rm{s}}^2 + \sigma _{\rm{T}}^2} }}} \right)} \end{array} $ | (11) |
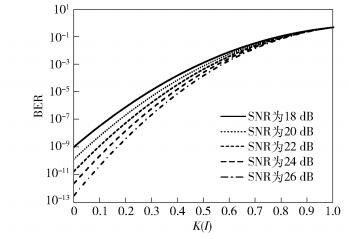
根据上述公式和SNR的取值范围,仿真出误码率和k(I)之间的关系曲线,其仿真结果如图 2所示.
|
图 2 误码率和k(I)关系曲线 |
由仿真结果可以看出,误码率与“1”电平错变到“0”电平的概率k(I)成正比,而干扰功率与合法信号功率比越大,k(I)越大;干扰功率比越大,SNR越小,这些都会导致系统误码率增大.
2 实验验证透明光网络耦合干扰系统主要由码型发生器、直接调制激光器、干扰激光光源,掺铒光纤放大器、耦合器、光电探测器、误码分析仪组成.其中,码型发生器和直调激光器组成发射机,将伪随机码加载到激光载波上,用以产生合法信号;激光控制器、干扰激光器组成干扰激光光源,通过调节激光控制器,可实现干扰激光的波长调谐以及功率变化.采用耦合器实现信号串扰,最终干扰后的光信号进入光电探测器中,使用误码分析仪对耦合干扰系统中信号质量进行分析,从而量化干扰激光光源对合法信号的影响.
实验过程中,首先由码型发生器产生伪随机码,然后直接调制激光器将伪随机码加载到激光中,得到合法信号;激光控制器控制激光器产生干扰源,进入掺饵光纤放大器和第一可调衰减器(VA1,variable attenuator),得到功率可调的干扰信号;合法信号和干扰信号注入到50/50耦合器中.其中,干扰信号95%的光功率进入耦合器干扰合法信号,5%的光功率进入光功率计,用以读取干扰源的输出功率.最后激光进入第二可调衰减器(VA2),并被光电探测器转换成电信号后进行误码分析.
DML由驱动电路产生的恒定55mA的电流驱动.直接调制激光器输出功率为1.61dBm,中心波长为1551.04nm.驱动电路中的集成温度控制电路,使激光器温度保持在室温25℃.为减小干扰激光器所需调节范围,选择在25℃时中心波长为1550.95nm,谱宽范围为1550.92~1550.97nm的窄线宽半导体激光器.耦合干扰实验中,首先,需要对干扰信号的中心波长进行移动,使干扰信号与合法信号中心重合.调节温度使干扰激光器温度达到27℃时,中心波长将移动至1551.04nm.同时需要对干扰信号进行功率调节,驱动电流的方式虽然可以改变功率,但是会造成温度增加,影响中心波长.所以为了调节耦合干扰源功率,并保持干扰激光的波长不变,选用掺铒光纤放大器和可变衰减器来调节干扰激光的输出功率.其中,掺铒光纤放大器、可变衰减器等相关光器件参数如表 1所示.
|
|
表 1 实验主要参数 |
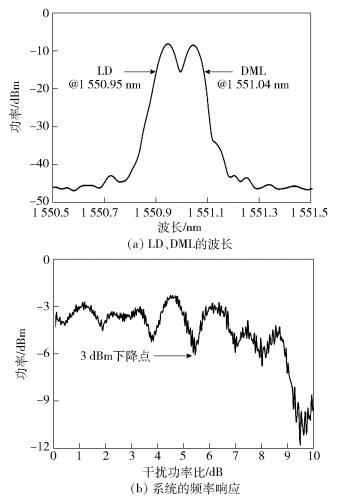
图 3(a)所示为25℃时LD和DML的波长;图 3(b)所示为测试系统的频率响应.对系统与耦合干扰功率比、误码率、PD最低接收功率之间的关系进行了实验.
|
图 3 激光器和系统性能测试图 |
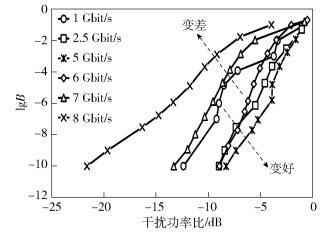
P为光功率,PLD为干扰激光器的功率,PDML为合法信号输出功率,IPR=10lg(PLD/PDML)为干扰源对合法信号的干扰功率比,简称干扰功率比.实验链路采用如图 1所示的耦合干扰链路,干扰源部分中方括号内为光纤,不加外调制.实验中,PD的接收功率保持在最佳范围,干扰功率比越大,SNR越低,误码率越高.图 4所示为调节干扰激光功率以及流量速率分别在1、2.5、5、6、7和8Gbit/s情况下得到的干扰功率比与误码率关系的实验结果.当IPR趋向于无穷小时,即PDML远大于PLD时,系统通信不受影响,lgB=-∞;随着IPR的增大,即PLD的增加,系统通信的误码率逐渐增大.当IPR增大到趋近于0时,即PLD=PDML时,通信中断,lgB=0.
|
图 4 耦合干扰功率比与lgB的实验结果 |
实验对不同传输速率下的干扰功率比和误码率关系进行了验证,实验结果均表明,合法信号功率一定时,干扰功率比越大,误码率越高.
2.2 传输速率对误码率的影响系统的误码率会随着不同的传输速率而变化.由图 4可看出,当IPR一定时,传输速率从1Gbit/s增加到5Gbit/s过程中,传输速率升高,耦合干扰对误码率的影响减弱,误码率减小.当传输速率从5Gbit/s增加到8Gbit/s过程中,传输速率升高,误码率增加.由于传输速率在光谱上由合法信号峰值在光载波中心波长两侧分布情况所表征,而在干扰激光的中心波长与DML中心波长相等的情况下,信号峰值的分布决定了干扰信号能否淹没合法信号.传输速率与信号峰值分布的关系推导如下.
由频率和波长的关系公式
| $ f = \frac{c}{\lambda } $ |
可推得两中心波长λ1和λ2频率差为
| $ \Delta f = \frac{{\left( {{\lambda _1} - {\lambda _2}} \right)c}}{{{\lambda _1}{\lambda _2}}} = \frac{{\Delta \lambda c}}{{{\lambda _1}{\lambda _2}}} $ | (12) |
其中Δf为光信号所调制的传输信号速率.由式(12)可知,激光光源调制信号后,传输速率Δf在光谱上与光源波长关系为
| $ \Delta \lambda = \frac{{\Delta f{\lambda ^2}}}{c} $ | (13) |
干扰源和合法信号的中心波长为1551.04nm,干扰信号的谱宽为0.05nm,约±0.025nm.当传输速率为1Gbit/s时,由式(13)计算出信号峰值出现在中心波长±0.008nm范围,合法信号峰值被干扰信号完全覆盖,干扰信号淹没合法信号,干扰激光与合法信号无法分离.当传输速率为5Gbit/s,信号峰值出现在中心波长±0.04nm.干扰信号无法覆盖合法信号峰值,系统的误码率降低.当传输速率为8Gbit/s时,信号峰值出现在中心波长的±0.064nm范围,虽然信号能够分开,但是由通信系统的频率响应特性决定带宽限制成为影响误码率的主要因素,由图 3(b)所示.
由实验结果可知,在通信系统带宽范围内,传输速率增加,干扰信号与合法信号在频域上间距增大,干扰信号对合法信号干扰程度降低,系统误码率减小.当传输速率大于系统带宽后,超过系统传输范围,误码率急剧增大.
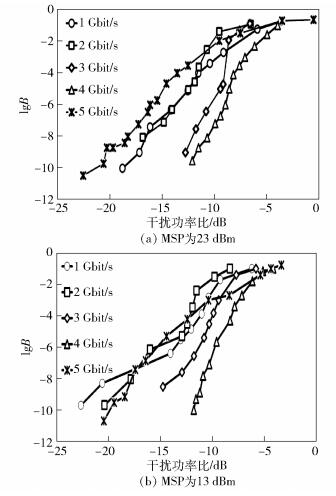
2.3 加载微波信号的干扰源对误码率的影响通过实验研究了加载模拟信号的干扰激光对通信系统质量的影响,其链路如图 1所示,其中干扰源部分的方括号内采用矢量网络分析仪和马曾调制器,用以在干扰激光上加载调制信号.实验结果如图 5所示,当微波源功率(MSP,microwave source power)为23dBm或13dBm时,随着传输速率增加,干扰信号对合法信号干扰程度降低,系统误码率减小,趋势与图 4类似.但是,与图 4不同的是,当传输速率增大到5Gbit/s时,系统误码率急剧恶化.说明加载了微波信号后的干扰源限制了系统的最高传输速率.
|
图 5 耦合干扰功率比与lgB的变化曲线 |
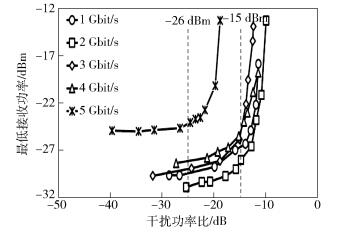
根据ITU-T 957规定,通信系统误码率小于等于10-10时,系统才能实现基本通信.图 6显示当误码率为10-10时耦合干扰功率比和PD最低接收功率之间的关系.当耦合干扰功率比增加,为保持误码率为10-10,PD需要更高的输入光功率,PD的最低接收功率变高.当传输速率从1Gbit/s增加到4Gbit/s过程中,当IPR < -15dB时,最低接收功率几乎保持不变;当IPR>-15dB时,PD最低接收功率会迅速增加.这是因为当IPR>-15dB,耦合干扰功率比对光网络链路的影响较大,最低接收功率随IPR的增大上升明显,IPR=-15dB是该系统速率在4Gbit/s以内的干扰阈值功率.同样的分析可知,当传输速率为5Gbit/s时,IPR阈值为-26dB.
|
图 6 耦合干扰功率比与PD最低接收功率实验结果 |
实验结果表明,当传输速率低于4Gbit/s,IPR的耦合功率阈值约为-15dB.当传输速率为5Gbit/s时,耦合干扰功率比阈值约为-26dB.假设干扰源与合法信号的波长、功率均一致,那么如果透明光器件通过掺杂等方式添加隔离层,且隔离度大于这一干扰阈值时,干扰源几乎不对合法信号产生影响.因此,当传输速率小于5Gbit/s,器件隔离度应大于15dB;当传输速率大于5Gbit/s,器件隔离度应大于26dB.
3 结束语针对透明光网络易受干扰的问题,提出了耦合干扰研究方法,从传输速率、干扰功率比和最低接收功率验证了干扰源对通信系统传输质量的干扰现象,有助于检查干扰源并预防其对合法信号的干扰.实验实现了1Gbit/s~8Gbit/s速率的传输通信,证明了以下3点. 1)在系统带宽范围内,传输速率增大,系统误码率减小.当传输速率大于系统带宽后,误码率急剧增大.如果出现合法信号传输速率增加而误码率先降低后升高的现象,说明检查出了合法信号受到信号干扰. 2)干扰功率比越大,通信系统质量越差.模拟信号加载到干扰源上,会影响通信系统的最高传输速率,但对整体通信质量影响不明显. 3)系统正常通信时,干扰功率比大于一定阈值后,系统最低接收功率急剧上升.此干扰阈值的绝对值对透明光器件隔离层的制作具有指导意义.透明光器件隔离度大于干扰阈值绝对值时,能预防干扰源对合法信号的干扰.最终,基于耦合干扰法成功研制了耦合干扰系统样机,为光网络安全性检查和防护提供了实验样机和平台.
| [1] | Schenk D, Krummrich P M. A novel approach to reduce the impact of physical layer restrictions in dynamically switched transparent optical networks[J]. Journal of Lightwave Technology, 2016, 34(9): 2304–2310. |
| [2] | Cao X J, Anand V, Qiao C M. Framework for waveband switching in multigranular optical networks:part Ⅰ-multigranular cross-connect architectures[J]. Journal of Optical Networking, 2006, 5(12): 1043–1055. |
| [3] | Skorin-Kapov N. Attack-aware planning and optimization in transparent optical networks[C]//2010 Asia Communications and Photonics Conference and Exhibition. Shanghai: IEEE, 2010: 79890A-1-79890A-4. |
| [4] | Skorin-Kapov N, Furdek M, Zsigmond S, et al. Physical-layer security in evolving optical networks[J]. IEEE Communications Magazine, 2016, 54(8): 110–117. |
| [5] | Medard M, Marquis D, Barry R A, et al. Security issues in all-optical networks[J]. IEEE Network, 1997, 11(3): 42–48. doi: 10.1109/65.587049 |
| [6] | Huang S W, Baba K I, Murata M, et al. A study on cycle attack by multiaccess interference in multigranularity OCDM-based optical networks[J]. Journal of Lightwave Technology, 2008, 26(14): 2064–2074. doi: 10.1109/JLT.2008.919483 |
| [7] | Deng Mingliang, Yi Xingwen, Zhang Hongbo, et al. Nonlinearity impact on in-band crosstalk penalties for 112-Gb/s PDM-CO-OFDM transmission[C]//2012 Asia Communications and Photonics Conference. Guangzhou: IEEE, 2012: 1-3. |
| [8] | Hu Q K, Kim H, Kim C H. Impact of receiver on in-band crosstalk-induced penalties in differentially phase-modulated signals[J]. Journal of the Optical Society of Korea, 2016, 20(2): 223–227. |
| [9] | Sakaguchi J, Awaji Y, Wada N, et al. 109-Tb/s (7×97×172-Gb/s SDM/WDM/PDM) QPSK transmission through 16. 8 km homogeneous multi-core fiber[C]//2011 IEEE Optical Fiber Communication Conference and Exposition and the National Fiber Optical Engineers Conference. Los Angeles: IEEE, 2011: 1-3. |
| [10] | Pan J, Isautier P, Filer M, et al. Addition of in-band crosstalk to the Gaussian noise model[C]//2015 Optical Fiber Communications Conference and Exhibition. Los Angeles: IEEE, 2015: 1-3. |
| [11] | Rebola J L, Cartaxo A V T. Estimating the performance of DD OFDM optical systems impaired by in-band crosstalk using the moment generating function[J]. Journal of Lightwave Technology, 2016, 34(10): 2562–2570. doi: 10.1109/JLT.2016.2542586 |
| [12] | Oliveira J C R F, Silva R, Silva E P, et al. Crosstalk penalties analysis in mixed line transmission rates (10G-OOK/40G-DQPSK/112G-DP-QPSK/224G-DP-16-QAM) optical flexible grid networks[J]. Microwave & Optical Technology Letters, 2013, 55(1): 119–122. |
| [13] | Winzer P J, Gnauck A H, Konczykowska A, et al. Penalties from in-band crosstalk for advanced optical modulation formats[C]//2011 37th European Conference and Exhibition on Optical Communications. Geneva: IEEE, 2011: 1-3. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6065992 |
| [14] | Rejeb R, Leeson M S, Green R J. Fault and attack management in all-optical networks[J]. IEEE Communications Magazine, 2006, 44(11): 79–86. doi: 10.1109/MCOM.2006.248169 |
| [15] | Yang Yuqiang, Han Qiqi, Tan Liying, et al. Research on bit error rate in the presence of local wavefront aberration in intersatellite laser communications[J]. Journal of Lightwave Technology, 2011, 29(19): 2893–2898. |
| [16] | Pointurier Y, Brandt-Pearce M, Subramaniam S. Analysis of blocking probability in noise and crosstalk impaired all-optical networks[J]. Journal of Optical Communications and Networking, 2009, 1(6): 543–554. doi: 10.1364/JOCN.1.000543 |
| [17] | Mrabet H, Attia R. BER and SNR analysis of optical network-on-chip using WCDMA codes[C]//2014 IEEE 15th International Conference on Sciences and Techniques of Automatic Control & Computer Engineering. Hammamet: IEEE, 2014: 996-1000. http://ieeexplore.ieee.org/document/7086673/ |


