稀疏码分多址接入(SCMA)方案映射矩阵维度太小时,短环和规则度分布的SCMA映射矩阵与存在远近效应的环境不能很好地匹配,为此,提出一种新型的非正交多址接入方案——低密度叠加编码调制(LDSM).该方案设计了更加稀疏的非规则度分布映射矩阵,带来分集增益和编码增益,提高整体方案性能的同时,对边缘用户的性能也有所提高.在独立瑞利衰落信道下,通过平均互信息的分析,从理论上证明了LDSM方案较SCMA方案有一定的信噪比增益.仿真结果证明,在远近功率差为10 dB,过载为150%时,小规模的LDSM方案和大规模LDSM方案较SCMA方案的整体用户性能分别能获得2.3 dB和2.46 dB的增益.
There may exist short cycles if the matrix dimensions of sparse code multiple access (SCMA) are small, and the regular mapping matrix of SCMA doesn't take near-far effect into consideration. Therefore, a novel uplink non-orthogonal multiple access scheme named low density superposition modulation (LDSM) scheme is proposed to construct a sparser and irregular mapping matrix. The proposed scheme can improve the overall performance and the edge users' performance for it can get diversity gain and coding gain. The analysis of the average mutual information demonstrates LDSM can get signal to noise ratio (SNR) gains over SCMA in theory. Simulation results show that when power difference is 10 dB and overloading is 150%, small dimensional and large dimensional LDSM can get 2.3 dB and 2.46 dB SNR gains over SCMA for overall performance. Both theoretic analysis and simulation results prove the performance of LDSM outperforms that of SCMA.
非正交多址接入(NOMA,non-orthogonal multiple access)方案可以有效地满足第5代移动通信(5G)的更严格的要求. NOMA方案的一个特点是可以实现过载,稀疏码分多址接入(SCMA,sparse code multiple access)方案是一种热门的NOMA方案,SCMA的编码比特直接映射成多维稀疏码本[1].由于码本的稀疏性,在接收端可以采用复杂度适中的信息传递译码算法(MPA, message passing algorithm)进行多用户检测[2].
目前有许多通过码本的设计提高SCMA的性能以及通过对译码算法的简化降低译码复杂度的研究工作.例如Taherzadeh等[3]和Cai等[4]针对SCMA码本设计提出许多有效的方法,Yang等[5]和Du等[6]基于MPA译码算法,提出许多降低译码复杂度的简化译码算法.然而这些研究都是基于小维度映射矩阵进行的,该映射矩阵中可能存在短环. MPA译码算法迭代次数超过最小环长(围长)的一半,节点间信息独立传递的假设就不成立,这将降低译码准确性[7].近来,也有研究者针对SCMA的性能进行分析. Bao等[8]在独立瑞利衰落的上行多址接入信道和下行广播信道下,对任意多维星座SCMA的差错性能进行研究,但他们研究的SCMA映射矩阵的设计并未考虑远近效应的影响.总之,目前很少有研究者针对SCMA映射矩阵进行设计,尽管在采用MPA译码算法时,映射矩阵的特性极大地影响译码性能. MPA译码算法与低密度校验码(LDPC, low-density parity check)的和积译码算法[9]有非常类似的特点,众所周知,LDPC校验矩阵的围长和度分布对其译码性能有决定性的影响. LDPC校验矩阵维度较小时,则会存在短环,在采用和积译码算法进行译码时,短环的存在会使错误值回传,增加错误译码的概率,从而降低译码性能[7].此外,规则的SCMA映射矩阵与存在远近效应的环境不能很好地匹配.在LDPC码中度大的变量节点连接较多的校验节点,在和积迭代译码的过程中它们能接收到更多的置信信息,所以度大的变量节点误码率低于度小的变量节点误码率,这就是LDPC的不等保护准则[10].
基于以上LDPC校验矩阵特性的分析,提出一种新型的NOMA方案——低密度叠加编码调制(LDSM, low density superposition modulation),该方案的目的在于设计更加稀疏的非规则度分布映射矩阵,用以解决短环和远近效应的问题,该方案不仅能带来分集增益,还可以带来编码增益,在提高整体用户性能的同时,对边缘用户的性能也有所提高.
1 LDSM系统模型图 1所示为上行LDSM的系统结构模型.首先J个用户分别对信息比特序列uj=(u1j, u2j, …, uKj)进行信道编码,如果有需要则进行速率匹配,然后对编码比特进行M-PSK/QAM调制,得到符号向量xj=(x1j, x2j, …, xLj),其中L=K/R/lb|X|,R为码率,X为调制星座点的集合,|X|为星座集合的大小.目前大多数的NOMA方案采用的映射矩阵维度较小,极有可能存在短环,这必将导致在采用MPA译码时,译码性能的下降.为了构造更加稀疏的大维度映射矩阵,在LDSM方案中可采用多个调制符号映射到多个数据流的方式进行LDSM编码.每个用户都可以将所有的L个符号映射到对应的数据流,每个用户同时占用L个数据流的方案叫作大规模LDSM方案.如图 2所示,dv定义为变量节点的度,也就是一个数据流能够占用的子载波个数.每个用户的调制符号通过编码得到编码向量
| $ \mathit{\boldsymbol{z}}_m^j = x_m^j{\mathit{\boldsymbol{f}}_{\left( {j - 1} \right)L + m}} $ | (1) |

|
图 1 上行LDSM的系统结构框图 |

|
图 2 LDSM编码过程 |
其中f(j-1)L+m为大规模LDSM映射矩阵F的第(j-1)L+m列.因为映射矩阵的维度足够大,编码向量中的符号元素更加分散,所以在衰落信道条件下,LDSM方案能够获得一定的分集增益.在LDSM系统中,渐进添边(PEG, progressive edge-growth)[11]算法可以用来构造映射矩阵. PEG通过逐步在变量节点和校验节点之间添加边来得到具有尽可能大围长的Tanner图以达到降低LDPC码误码率的目的.该构造LDPC码校验矩阵的方法比较简单、便捷,可保证围长的下界,并且可构造任意码率和码长的LDPC码校验矩阵,是一种重要的构造LDPC码校验矩阵的方法,故可用该方法构造稀疏映射矩阵:
| $ {\mathit{\boldsymbol{F}}_{L{N_{\rm{c}}} \times LJ}} = \left[ {\begin{array}{*{20}{c}} 0&1&1& \cdots &1&0\\ 1& \vdots &1&0&0&1\\ \vdots &1& \vdots&\ddots&\vdots&\vdots \\ 1&0&0& \cdots &1&0 \end{array}} \right] $ | (2) |
其中:L是用户对应的调制符号总数,Nc为载波数.通过如图 2所示的LDSM编码过程得到编码向量
| $ {\mathit{\boldsymbol{z}}_j} = \sum\limits_{m = 1}^L {\mathit{\boldsymbol{z}}_m^j} = \sum\limits_{m = 1}^L {x_m^j{\mathit{\boldsymbol{f}}_{\left( {j - 1} \right)L + m}}} = {\mathit{\boldsymbol{F}}_j}\mathit{\boldsymbol{x}}_j^{\rm{T}} $ | (3) |
其中Fj是映射矩阵F的一部分,即用户j的调制符号对应的L个数据流在矩阵中所占的所有列. LDSM编码向量zj是用户j的所有调制符号对应编码向量的和.
鉴于SCMA的规则映射矩阵与存在远近效应的环境不匹配,LDSM构造非规则映射矩阵,该矩阵保证边缘用户对应的变量节点的度大于中心用户对应的变量节点,类似于LDPC的不等保护准则.不同类型用户对应变量节点的度的关系为
| $ \frac{{{d_{{\rm{ve}}}}}}{{{d_{{\rm{vc}}}}}} = {10^{\frac{{{P_{\rm{d}}}}}{{10}}}}\frac{{{R_{\rm{e}}}}}{{{R_{\rm{c}}}}} $ | (4) |
其中:dvc和Rc分别定义为中心用户变量节点的度和编码码率,类似地,dve和Re定义为边缘用户变量节点的度和编码码率;Pd为远近用户的功率差.
为了证明小维度LDSM方案也可以获得编码增益,设计小维度LDSM.小维度LDSM方案中,每用户的2个调制符号映射到2个数据流上.以Nc=4,J=6为例,如果功率差Pd=10dB,则构造的小维度映射矩阵F为
| $ {\mathit{\boldsymbol{F}}_{8 \times 12}} = \left[ {\begin{array}{*{20}{c}} 1&1&0&1&0&1&0&1&0&0&0&1\\ 1&1&0&0&1&0&1&0&1&0&0&1\\ 1&0&1&0&1&1&0&0&0&1&0&0\\ 0&1&1&1&0&0&1&0&1&0&0&0\\ 0&1&1&1&1&0&0&0&0&0&1&0\\ 0&1&1&0&1&1&0&0&0&1&0&0\\ 1&0&0&1&1&1&0&1&0&0&0&0\\ 1&0&1&1&0&1&0&0&0&0&1&0 \end{array}} \right] $ | (5) |
其中ρ5=ρ2=50%,ρi定义为度dv=i的变量节点占总节点数的比例.式(5)对应的因子图如图 3所示,从图中可以看出,边缘用户对应变量节点的度大于中心用户对应变量节点的度,该设计类似LDPC的不等保护准则,不仅可以提高整体用户的性能还可以提高边缘用户的性能.

|
图 3 Nc=4、J=6的小规模LDSM映射矩阵对应因子图 |
如图 1所示,在接收端,采用适中译码复杂度的MPA译码算法进行多用户检测,并利用信道译码器反馈的外信息λe进行外迭代,以提高系统性能,λp为MPA译码器传递给信道译码器的对数似然比,
| $ \mathit{\boldsymbol{y}} = \sum\limits_{j = 1}^J {{\rm{diag}}\left( {{\mathit{\boldsymbol{h}}_j}} \right){\mathit{\boldsymbol{z}}_j}} + \mathit{\boldsymbol{n}} $ | (6) |
其中
平均互信息(AMI, average mutual information)反映了给定条件下无差错传输的最大速率,同时考虑了多种因素,如星座点结构、信噪比、信道模型等.因此利用AMI作为工具从理论上分析LDSM方案较SCMA方案可取得SNR增益.基于每个子载波的编码调制系统的平均互信息(CM-AMI)可表示为[12]
| $ \begin{array}{*{20}{c}} {I = \frac{1}{{{N_{\rm{c}}}}}I\left( {\mathit{\boldsymbol{s}};\mathit{\boldsymbol{y}}\left| \mathit{\boldsymbol{h}} \right.} \right) = \frac{1}{{{N_{\rm{c}}}}}\left( {H\left( \mathit{\boldsymbol{s}} \right) - H\left( {\mathit{\boldsymbol{s}}/\mathit{\boldsymbol{yh}}} \right)} \right) = }\\ {\frac{1}{{{N_{\rm{c}}}}}\left( {p - {E_{\mathit{\boldsymbol{s}},\mathit{\boldsymbol{y}},\mathit{\boldsymbol{h}}}}\left[ {{\rm{lb}}\frac{{\sum\limits_{\mathit{\boldsymbol{x}} \in \mathit{\Omega }} {P\left( {\mathit{\boldsymbol{y}}\left| \mathit{\boldsymbol{s}} \right.,\mathit{\boldsymbol{h}}} \right)} }}{{P\left( {\mathit{\boldsymbol{y}}\left| \mathit{\boldsymbol{s}} \right.,\mathit{\boldsymbol{h}}} \right)}}} \right]} \right)} \end{array} $ | (7) |
| $ \begin{array}{*{20}{c}} {P\left( {\mathit{\boldsymbol{y}}\left| \mathit{\boldsymbol{s}} \right.,\mathit{\boldsymbol{h}}} \right) = \frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}{\sigma ^2}} \right)}^{{N_{\rm{c}}}{N_{\rm{r}}}}}}} \times }\\ {\exp \left( {\sum\limits_{k = 1}^{{N_{\rm{c}}}{N_{\rm{r}}}} {\frac{{ - {{\left| {{y_k} - \sum\limits_{j = 1}^J {{h_{kj}}{z_{jk}}} } \right|}^2}}}{{2{\sigma ^2}}}} } \right)} \end{array} $ | (8) |
式(7)的含义为基于每个子载波的编码调制系统的AMI可由发送信号s的熵H(s)和已知接收信号y和信道系数h条件时的条件熵H(s/yh)计算求得.式(8)计算发送和接收符号都为向量时的条件概率,其中Nr为接收天线数,s为所有用户发送的符号构成的向量,Ω定义为多用户星座组成的高维星座点,p=lb|Ω|=Jlb|X|,|Ω|为集合Ω的大小,E[·]为求均值运算.
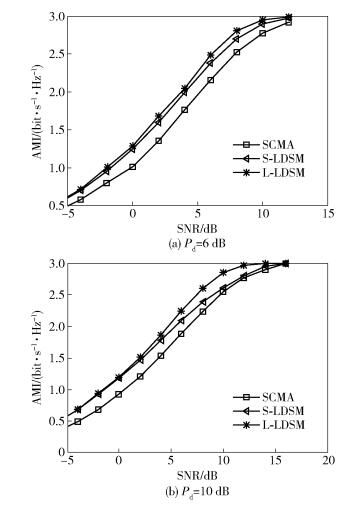
以功率差Pd=6dB和Pd=10dB为例,在独立瑞利信道,1发2收天线配置下,通过蒙特卡洛仿真从理论上证明所提的LDSM方案较SCMA方案可获得SNR增益.从图 4(a)中可以看出,在每用户谱效为0.1875bit·s-1·Hz-1(对应物理层仿真条件)时,S-LDSM和L-LDSM较SCMA方案分别可以获得1.7dB和1.8dB增益.从图 4(b)可见AMI性能对比结果,在每用户谱效为0.15625bit·s-1·Hz-1(对应物理层仿真条件)时,S-LDSM和L-LDSM较SCMA方案均可获得2.5dB的增益.
|
图 4 不同功率差下不同方案的AMI对比 |
以SCMA[1]作为参考方案,常用Nc=4,J=6的映射矩阵,为
| $ {\mathit{\boldsymbol{F}}_{4 \times 6}} = \left[ {\begin{array}{*{20}{c}} 1&1&1&0&0&0\\ 1&0&0&1&1&0\\ 0&1&0&1&0&1\\ 0&0&1&0&1&1 \end{array}} \right] $ | (9) |
SCMA 4点常用码本可由文献[3]所示方法构造,该方法构造的同一个码本的所有码字在相同的2个维度为零,可见该码本不适合具有超过2个非零维度的映射矩阵.在存在远近效应的仿真中SCMA用到开环功控.
表 1列出了具体的仿真参数设置. LDPC码采用PEG构造的规则(3, 6)度分布的LDPC码.用户数设置为6用户和8用户2种场景,其过载系数分别为150%和200%.过载为150%时SCMA映射矩阵维度为4×6,S-LDSM矩阵维度8×12,L-LDSM矩阵维度768×1152.过载为200%时,SCMA映射矩阵维度为4×8,S-LDSM矩阵维度8×16,L-LDSM矩阵维度768×1536.过载为150%,Pd=6dB时,LDSM方案变量节点度分布为ρ4=ρ2=50%,L-LDSM对应的围长为10,而SCMA对应的围长只有6,大围长的映射矩阵可以带来一定的编码增益. Pd=10dB时,LDSM方案变量节点度分布为ρ5=ρ2=50%,L-LDSM对应的围长为8.
|
|
表 1 上行1发2收链路级仿真参数 |
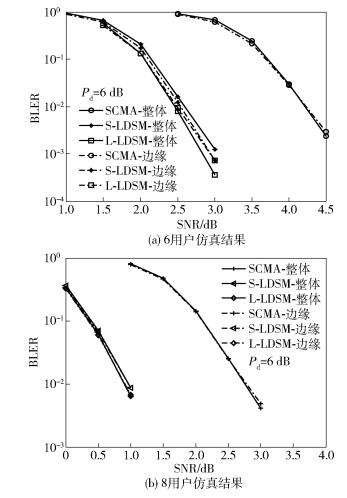
图 5所示为上行1发2收独立瑞利信道下,Pd=6dB,6用户和8用户2种场景下各种方案的误块率(BLER,block error rate)性能对比. 6用户,BLER为10-2时, 对于整体用户平均性能,S-LDSM和L-LDSM较SCMA分别能获得1.79dB和1.85dB的增益.对于边缘用户平均性能,S-LDSM和L-LDSM较SCMA的增益分别为1.81dB和1.86dB. 8用户,BLER为10-2时, 对于整体用户平均性能, S-LDSM和L-LDSM较SCMA分别能获得1.64dB和1.75dB的增益.对于边缘用户平均性能,S-LDSM和L-LDSM较SCMA的增益分别为1.65dB和1.74dB.通过以上分析可得,所提的LDSM方案在不同用户数场景下较SCMA都有较大的性能增益,证明所提方案的鲁棒性较强.
|
图 5 不同用户数,不同方案误块率性能 |
图 6所示为上行1发2收独立瑞利信道下,Pd=10dB,BLER为10-2时整体用户的平均性能, S-LDSM和L-LDSM较SCMA分别能获得2.3dB和2.46dB的增益.对于边缘用户平均性能,S-LDSM和L-LDSM较SCMA的增益分别为2.18dB和2.43dB.

|
图 6 不同方案误块率性能 |
通过比较图 4~图 6可知理论分析和仿真结果相对应,表明提出的LDSM方案优于传统SCMA方案.
4 结束语对于SCMA方案,当映射矩阵维度较小时可能存在短环,短环的存在会导致采用MPA迭代译码算法时回传错误值,增大译码错误的概率,降低译码性能.此外,规则度分布的SCMA映射矩阵与存在远近效应的环境不能很好地匹配.提出一种新型的低密度叠加编码调制NOMA方案,该方案的目的在于设计更加稀疏的非规则映射矩阵,这样不仅能够带来分集增益,还可以带来编码增益.提高整体用户性能的同时,对边缘用户的性能也有所提高.理论分析和仿真结果都证明了所提方案较SCMA方案有一定的性能增益.
| [1] | Nikopour H, Baligh H. Sparse code multiple access[C]//IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications. London: IEEE Press, 2013: 332-336. |
| [2] | Hoshyar R, Wathan F P, Tafazolli R. Novel low-density signature for synchronous CDMA systems over AWGN channel[J]. IEEE Transactions on Signal Process, 2008, 56(4): 1616–1626. doi: 10.1109/TSP.2007.909320 |
| [3] | Taherzadeh M, Nikopour H, Bayesteh A, et al. SCMA codebook design[C]//2014 IEEE 80th Vehicular Technology Conference. Vancouver: IEEE Press, 2014: 1-5. |
| [4] | Cai Donghong, Fan Pingzhi, Lei Xianfu, et al. Multi-dimensional SCMA codebook design based on constellation rotation and interleaving[C]//2016 IEEE 83rd Vehicular Technology Conference. Nanjing: IEEE Press, 2016: 1-5. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7504356 |
| [5] | Yang Lin, Liu Yunyun, Siu Y M. Low complexity message passing algorithm for SCMA system[J]. IEEE Communications Letters, 2016, 20(12): 2466–2469. doi: 10.1109/LCOMM.2016.2609382 |
| [6] | Du Yang, Dong Binhong, Chen Zhi, et al. A fast convergence multiuser detection scheme for uplink SCMA systems[J]. IEEE Wireless Communications Letters, 2016, 5(4): 388–391. doi: 10.1109/LWC.2016.2565581 |
| [7] | Fossorier M P C. Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1788–1793. doi: 10.1109/TIT.2004.831841 |
| [8] | Bao Jinchen, Ma Zheng, Karagiannidis G K, et al. Joint multiusr detection of multidimensional constellations over fading channels[J]. IEEE Transactions on Communications, 2017, 65(1): 161–172. |
| [9] | Kschischang F R, Frey B J, Loeliger H-A. Factor graphs and the sum-product algorithm[J]. IEEE Transactions on Information Theory, 2001, 47(2): 498–519. doi: 10.1109/18.910572 |
| [10] | Rahnavard N, Pishro-Nik H, Fekri F. Unequal error protection using partially regular LDPC codes[J]. IEEE Transactions on Communications, 2007, 55(3): 387–391. doi: 10.1109/TCOMM.2007.892436 |
| [11] | Hu X-Y, Eleftheriou E, Arnold D-M. Progressive edge-growth tanner graphs[C]//Global Telecommunications Conference. San Antonio: IEEE Press, 2001: 995-1001. |
| [12] | Xie Qiuliang, Song Jian, Peng Kewu, et al. Coded modulation with signal space diversity[J]. IEEE Transactions on Wireless Communications, 2011, 10(2): 660–669. doi: 10.1109/TWC.2011.120810.100951 |


