2. 北方自动控制技术研究所, 太原 030006
针对数据压缩方法计算复杂度高、压缩效率和数据恢复准确率较低的情况,提出一种基于簇头-基站分离式结构的无线传感器网络(WSN)数据压缩方法.该方法在WSN单层分簇结构的基础上,首先要求感知节点等时间间隔采集数据,并分段发送;然后采用原有空间相关性数据压缩方法对簇头节点接收的数据进行空间噪声及冗余的消除;最后在基站采用改进的灰色模型进行数据恢复.另外,通过实验分析不同段长及压缩率情况下,灰色模型、灰色马尔可夫链模型以及改进的灰色模型对数据的恢复效果,给出算法的最优模型和段长.仿真结果表明,提出的方法较已有线性类WSN数据压缩方法可显著提高压缩精度和效率.
2. North Automatic Control Technology Institute, Taiyuan 030006, China
In view of high computational complexity, low compression efficiency and data recovery rate of current data compression methods of wireless sensor network, a wireless sensor networks (WSN) data compression method based on a cluster head base station separation structure is proposed. Based on the monolayer cluster structure of WSN, the method requests the terminal sensor node to collect data at equal intervals and transmit data in segments at first. Then the spatial correlation data compression method is performed to eliminate the space noise and space redundancy of data in cluster head node. Finally, the improved grey model is adopted for data recovery at the base station. In addition, the optimal model and segment length of the algorithm are given, through the experimental analysis of the data recovery effect of the improved grey model, the grey model and the grey Markov chain model. Experimental results show that, compared with the existing linear WSN data compression methods, the proposed method significantly improves the WSN compression accuracy and efficiency.
无线传感器网络(WSN, wireless sensor networks)具有迅速部署、自动组网、高隐蔽性以及高容错性等特点,但其节点的计算和存储能力以及电源能量等非常有限,研究WSN的数据压缩方法具有重要意义.
国内外已经有许多学者对计算复杂度相对较低的线性拟合方法进行了研究[1-2].翟双等[3]提出的两步压缩算法(TSC-SC, the two-step data compression algorithm based on sequence correlation)和陈岁生等[4]提出的基于提升小波变换和自适应多项式拟合的多模数据压缩算法(AMLP, adaptive multiple-modality data compression algorithm based on lifting wavelet and adaptive polynomial fitting)都是在数据相关性分组的基础上,在簇内节点和簇头进行数据压缩.王玲等[5]考虑感知数据的时间相关性,对基于分段线性回归模型的数据压缩方法进行了优化.张瑞瑞等[6]同时考虑了数据相关性(单个节点同一段时间内可以采集到温度、湿度、光照等多种类型的参数)、WSN结构及模型优化问题,提出了基于分段线性回归的数据压缩方法(PWLR, piece-wise linear regression).
近些年,一些预测类方法广泛应用于WSN研究,如灰色模型[7](GM, grey model)目前应用于WSN数据融合算法[8]、网络异常检测[9]及流量异常检测[10]研究.灰色模型改进后的灰色马尔可夫链模型,可用于WSN数据异常状态的预测[11]以及针对容迟网络路由算法的研究[12].
在研究多种线性拟合及预测类方法的基础上,笔者提出簇头-基站式的基于改进灰色模型的分段数据压缩方法(OEGMP, piecewise data compression method for odd and even grey model),利用灰色模型在WSN能量充足的基站对未传输数据的预测实现对WSN数据的压缩,使能源有限的WSN数据传输达到较高压缩率和精确度的目的.
1 预备知识 1.1 灰色模型灰色模型是由GM(1,1)对元素个数为n的可以反映对象特征的时间序列X(0)建模,以预测未来某一时刻的特征量.
通过对原始数据序列构造一阶累加序列和一阶累加紧邻序列,然后构建GM(1,1)模型一阶常微分方程并求解,在此基础上进行等间隔取样离散值,则可以求得模型下一时刻的预测值.
1.2 改进灰色模型对灰色模型改进的实质是通过抽取原始数据序列X(0)中序列号为奇数的数据Xo(0),再以奇序列Xo(0)为灰色模型原始数据进行建模,最终完成对X(0)中偶序列以及未来某一时刻特征量的预测,称改进的灰色模型为奇偶灰色模型(OEGM, odd and even grey model).
采用与1.1节同样的方法,构造数据一阶累加序列和一阶累加紧邻序列,然后对序列Xo(1)构建GM(1,1)模型微分方程并求解,相应地,等间隔取样离散值,则可求得模型对奇序列k时刻的预测值.
1.3 灰色马尔可夫链模型灰色马尔可夫(Markov)链模型是在灰色模型的基础上,对残差进行GM(1,1)建模,并采用马尔可夫链模型[13]对残差符号进行预测.
2 问题描述和网络模型 2.1 问题描述在监测区域中随机部署的WSN传感器节点,感知环境中的信息(温度、湿度等),并将信息发送到基站供用户使用.现需要在该背景下对WSN传感器节点的感知数据进行压缩.
2.2 网络模型所提出OEGMP算法的网络模型描述如图 1所示.算法要求感知节点按照等时间间隔采集数据,将数据序列分段后,发送每段数据奇序列至所在簇的簇头节点;然后对簇头接收的原始数据进行空间去噪及数据压缩[14],输出簇头所在区域的等时间间隔参数均值;最终在基站采用改进的灰色模型对每段未发送数据进行恢复.
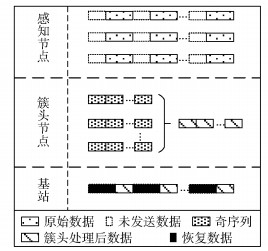
|
图 1 网络模型描述 |
由于WSN的基站资源供应方便,基站对WSN的能量损耗可以忽略,所以算法大部分的实现是在基站完成,只在簇头节点对原始数据进行空间相关性压缩.在传输相同数据量的情况下,与在感知节点进行全部WSN数据压缩的算法对比,所提算法造成的网络耗能大大降低.
3 算法描述 3.1 感知节点单个感知节点周期T内采集数据序列为Snode,为了在数据恢复过程中把握所采集数据随时间变化的特性,从而确保数据恢复精度,感知节点以段长l将数据分段,并发送每段前r(0<r<l)个数据的奇序列至本节点所在簇的簇头节点.
3.2 簇头节点WSN中同一簇内各节点同一时刻所感知的数据具有空间相关性.根据文献[14]将簇头节点的数据进行空间相关性压缩:首先去除簇内不同节点同一时刻数据的空间噪声;其次通过求取均值对数据进行压缩;最后将压缩后的等时间间隔的数据发送至基站.
3.3 基站各簇头将等时间间隔数据传送至基站,基站利用灰色模型,对接收数据Scluster进行建模.基站采用模型恢复数据时,需要感知节点分段发送每段前r个数据作为原始序列.
算法1 GM(1,1)对原始数据建模算法
输入:X(0) /*X(0)为基站接收到某个簇头节点的数据Scluster*/
输出:Sprediction
u =[a b]′;
X(1)=cumsum(X(0)); /*原始数据累加*/
r=length(X(0));
for i=1:(ro-1)
D(i)=(X(1)(i)+X(1)(i+1))/2; /*生成累加矩阵*/
end
/*计算待定参数的值*/
Y =X(0)/2; Y(1)=[];
Y=Y′;
B =[-D; ones(1, r-1)];
/*ones()生成的r-1个元素均为1*/
u =inv(B*B′)*B*Y; /*inv()求逆矩阵*/
u=u′; a=u(1);b=u(2);
/*恢复数据*/
F=[]; F(1)=X(0)(1); G=[];
G(1)=X(0)(1);
for i=2:(l)
F(i)=(X(0)(1)-b/a)/exp(a*(i-1))+b/a;
/*恢复X(1)的数据*/
G(i)=F(i)-F(i-1); /*恢复X(0)的数据*/
G(i)=2* G(i);
end
4 实验及仿真结果 4.1 性能参数1) 压缩效率
数据压缩率为压缩后的数据大小与原始数据大小的比值,定义WSN压缩算法数据压缩率为
| $ C={{C}_{\text{cluster}}}{{C}_{\text{sink}}}=\frac{1}{m}\frac{{{r}_{\text{o}}}}{l}~=\frac{{{r}_{\text{o}}}}{ml} $ | (1) |
其中:Ccluster为簇头节点处的数据压缩率,Csink为基站处采用灰色马尔可夫链的数据压缩率.
2) 数据恢复准确度
算法对数据的恢复精度以均方根误差E为衡量标准,均方根误差越小,则数据恢复精度越高.
| $ E=\sqrt{\frac{1}{n}\sum{{{\left( {{{\hat{d}}}_{t}}-{{d}_{t}} \right)}^{2}}}} $ | (2) |
其中:
实验采用Intel Berkeley Research Lab[15]提供的数据,通过Matlab平台来验证算法的可行性和有效性.算法OEGMP需要的等时间间隔数据是由Python程序处理得到的,时间间隔平均为3 min.
首先以数据恢复精度为性能指标分析不同段长时,改进灰色模型与灰色模型以及灰色马尔可夫链算法的压缩率和均方根误差关系以及数据分段传输过程中基站所采用模型的最优段长;然后以压缩率和数据恢复精度为性能指标,将所提算法OEGMP与文献[3]、文献[4]、文献[6]提到的算法TSC-SC、AMLP、PWLR进行对比分析.
4.3 实验结果1) 选择最优段长及模型
实验采用温度数据得到3种模型各自在段长为10、20、…、80时均方根误差与压缩率的关系,分别如图 2~图 4所示.
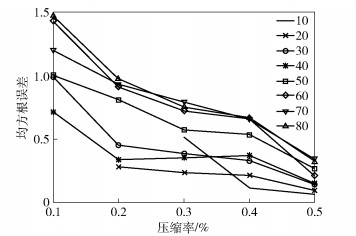
|
图 2 改进灰色模型恢复数据均方根误差与压缩率的关系 |

|
图 3 灰色模型恢复数据均方根误差与压缩率的关系 |
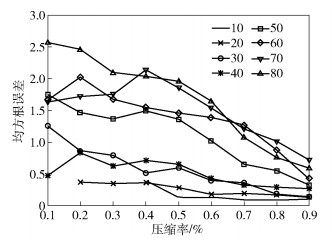
|
图 4 灰色马尔可夫链恢复数据均方根误差与压缩率的关系 |
以段长为变量分析:首先,灰色模型与灰色马尔可夫链模型情况较为相近,当段长较小时,灰色模型在低压缩率情况下的数据恢复精度较灰色马尔可夫链模型更高;而段长较大时,灰色马尔可夫链模型的数据恢复精度高于灰色模型.其次,不同段长情况下,改进的灰色模型在同一压缩率下的均方根误差始终低于其他2种模型,其原因是改进的灰色模型只使用奇序列对原始数据进行预测,在减小一定压缩率的情况下,恢复精度与传统灰色模型无较大差别.当改进的灰色模型只恢复原始数据的偶序列时,其压缩率达到最大值50%,所以图 4中改进灰色模型的曲线都处于压缩率小于0.5的范围内.
分段长度以及压缩率的大小决定基站算法的调用次数,进而对WSN能耗产生一定影响.所以,在分段长度较小且压缩率较高时或者分段长度较大时,若采用灰色马尔可夫链模型进行数据压缩,可使数据恢复精度相对较高的同时减小因算法调用次数而产生的网络耗能.
以基站所采用的算法(模型)类型分析:3种模型的均方根误差与压缩率关系曲线呈现相似情况,即随着段长增加,不同压缩率下的均方根误差逐渐增大.其中段长为10和20的曲线在较低压缩率时都没有得到均方根误差,原因在于压缩率过小导致每段的样本数据太小,灰色模型和灰色马尔可夫链模型都无法计算模型的参数.段长为30或40时,随压缩率变化,均方根误差大小无法确切判断,因此,若系统要求压缩率可达到10%时,可将段长确定在30~40之间.
综上所述,可根据系统要求的压缩率选择合适段长及模型,具体信息如表 1所示.
|
|
表 1 最优段长及模型选择 |
2) 与其他算法对比
所提OEGMP算法与算法TSC-SC、AMLP、PWLR进行对比,4种数据压缩方法的均方根误差随压缩率变化关系如图 5所示.
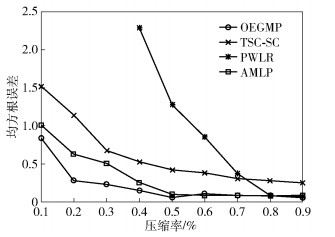
|
图 5 WSN数据压缩算法对比 |
从图 5可知,OEGMP算法对WSN数据压缩效果整体优于TSC-SC算法;在压缩率分别大于55%和80%时,OEGMP数据压缩精度与算法AMLP和PWLR相近.
5 结束语笔者对灰色模型、改进灰色模型和灰色马尔可夫链模型进行分析对比,选择将灰色模型应用于WSN数据压缩方法,并基于WSN的单层分簇结构融合已有数据压缩算法,提出一种基于改进的灰色模型的WSN数据压缩方法.该算法采用分段数据压缩,以适应采集数据随时间的变化,从而提高数据恢复精度.对算法进行实验仿真及性能分析,结果表明,基于空间相关性与灰色模型的WSN数据压缩方法,在较高压缩效率的条件下能够保证数据恢复精度,较原始传输策略显著减少数据传输量,可显著降低网络能量消耗,延长网络寿命,适用于具有空间相关性的应用环境,有较强扩展性.
| [1] | Deligiannakis A, Kotidis Y, Roussopoulos N. Dissemination of compressed historical information in sensor networks[J]. The International Journal of Very Large Data Bases, 2007, 16(4): 439–461. doi: 10.1007/s00778-005-0173-5 |
| [2] |
林蔚, 韩丽红. 无线传感器网络的数据压缩算法综述[J]. 小型微型计算机系统, 2012, 33(9): 2043–2048.
Lin Wei, Han Lihong. Summary of data compression algorithm in wireless sensor networks[J]. Journal of Chinese Computer Systems, 2012, 33(9): 2043–2048. |
| [3] |
翟双, 钱志鸿, 刘晓慧, 等. 无线传感器网络中基于序列相关性的数据压缩算法[J]. 电子与信息学报, 2016, 38(3): 713–719.
Zhai Shuang, Qian Zhihong, Liu Xiaohui, et al. Data compression algorithm based on sequence correlation for WSN[J]. Journal of Electronics & Information Technology, 2016, 38(3): 713–719. |
| [4] |
陈岁生, 卢建刚. 基于提升小波和自适应多项式拟合的传感器网络多模数据压缩算法[J]. 传感技术学报, 2013, 26(4): 550–557.
Chen Suisheng, Lu Jiangang. An adaptive multiple-modality sensor network data compression algorithm based on lifting wavelet and polynomial fitting[J]. Chinese Journal of Sensors and Actuators, 2013, 26(4): 550–557. |
| [5] |
王玲, 石为人, 石欣, 等. 基于时间相关性的无线传感器网络数据压缩与优化算法[J]. 计算机应用, 2013, 33(12): 3453–3456.
Wang Ling, Shi Weiren, Shi Xin, et al. Data compression and optimization algorithm for wireless sensor network based on temporal correlation[J]. Journal of Computer Applications, 2013, 33(12): 3453–3456. |
| [6] |
张瑞瑞, 杜尚丰, 陈立平, 等. 基于分段线性回归的传感器网络数据压缩传输方法研究[J]. 传感技术学报, 2015, 28(4): 531–536.
Zhang Ruirui, Du Shangfeng, Chen Liping, et al. Data compression method with piece-wise linear regression in WSN[J]. Chinese Journal of Sensors and Actuators, 2015, 28(4): 531–536. |
| [7] |
孙韩林, 金跃辉, 崔毅东, 等. 粗粒度网络流量的灰色模型预测[J]. 北京邮电大学学报, 2010, 33(1): 7–11.
Sun Hanlin, Jin Yuehui, Cui Yidong, et al. Large-time scale network traffic short-term prediction by grey model[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(1): 7–11. |
| [8] | Luo Xiong, Chang Xiaohui. A novel data fusion scheme using grey model and extreme learning machine in wireless sensor networks[J]. International Journal of Control Automation & Systems, 2015, 13(3): 539–546. |
| [9] |
刘洲洲, 李士宁. 采用压缩感知和GM(1, 1)的无线传感器网络异常检测方法[J]. 西安交通大学学报, 2017, 51(2): 40–46.
Liu Zhouzhou, Li Shining. An anomaly detection method for wireless sensor networks based on compressed sensing and GM (1, 1)[J]. Journal of Xi'an Jiaotong University, 2017, 51(2): 40–46. |
| [10] | Yu Qin, Lü Jibin, Jiang Lirui, et al. Traffic anomaly detection algorithm for wireless sensor networks based on improved exploitation of the GM(1, 1) model[J]. International Journal of Distributed Sensor Networks, 2016, 12(7): 2181256–2181256. doi: 10.1177/155014772181256 |
| [11] |
林蔚, 李波, 韩丽红. 基于二次灰色马尔可夫预测的WSN状态判定算法[J]. 计算机工程与科学, 2013, 35(8): 41–45.
Lin Wei, Li Bo, Han Lihong. State determination algorithm of WSN based on twice grey Markov forecasting[J]. Computer Engineering and Science, 2013, 35(8): 41–45. |
| [12] |
张文柱, 韩晓冬. 容迟网络中提高数据包转发方向性的路由算法[J]. 北京邮电大学学报, 2012, 35(4): 6–10.
Zhang Wenzhu, Han Xiaodong. Delay tolerant network routing algorithm to enhance the packet forwarding direction[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(4): 6–10. |
| [13] |
陈前斌, 黄晨, 唐伦. 异构网络负载感知的动态增强型干扰协调方案[J]. 北京邮电大学学报, 2015, 38(3): 39–42.
Chen Qianbin, Huang Chen, Tang Lun. Load-ware based dynamic enhanced inter-cell interference coordination scheme in heterogeneous networks[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(3): 39–42. |
| [14] |
王雷春, 马传香. 传感器网络中一种基于一元线性回归模型的空时数据压缩算法[J]. 电子与信息学报, 2010, 32(3): 755–758.
Wang Leichun, Ma Chuanxiang. A one-dimensional linear regression model based spatial and temporal data compression algorithm for wireless sensor networks[J]. Journal of Electronics &Information Technology, 2010, 32(3): 755–758. |
| [15] | Intel Berkeley research lab. Intel lab data[EB/OL]. 2004(2004-06-02)[2017-04-28]. http://db.csail.mit.edu/labdata/labdata.html. |


