2. 北京邮电大学 网络体系构建与融合北京市重点实验室, 北京 100876;
3. 北京邮电大学 计算机科学与技术学院, 北京 100876
针对通信信号业务种类识别问题,提出利用机器学习领域的线性回归算法和多项式拟合模型提取信号功率谱的多项式拟合因子作为信号的统一特征来构建训练集,并在深度学习平台keras上构建了全连接的神经网络分类器模型.相比传统的方法,新方法具有对无线电信号统一表征而无需对业务逐个提取个性化特征的优点.选取实际无线电监测数据中的码分多址(CDMA)上行、CDMA下行、增强型全球移动通信系统(EGSM)上行、EGSM下行、无线局域网(WLAN)以及长期演进(LTE)6种信号的功率谱数据作为数据集,通过验证得到了97%的分类准确率,并证明了该方法的可行性.
2. Computer Network Research Center, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. School of Computer Science and Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
Aiming at the problem of communication signal service type identification, the author proposes a polynomial fitting factor that extracts the power spectrum of the signal using the linear regression algorithm and the polynomial fitting model in machine learning field as a unified feature of the signal to construct the training set. A multi-layer fully connected neural network classifier model was built on depth learning platform. Compared with the traditional ones, this method has advantages of unifying the radio signal without the need of individual service to extract the personalized features. The power spectrum data of code division multiple access(CDMA) uplink, CDMA downlink, extended global system for mobile(EGSM) uplink, EGSM downlink, wireless local area networks (WLAN) and long time evolution (LTE) signals in the actual radio monitoring data are selected as data set, and 97% classification accuracy is verified. that this method is proven feasible.
信号识别是当今无线通信领域中的研究热点.如今对信号识别的研究大多都是调制模式识别,并且主要的研究方法是针对不同种类的调制信号提取不同的专家特征进行识别[1-5].然后依据提取的不同专家特征构建协同表决模型进行分类[2-4].但是随着物联网的诞生,海量设备接入和更多低功率广域业务信号的应用已经成为必然,同时给通信系统带来了全新的挑战.因为各种不同的业务信号采用了更为复杂的多重调制方式甚至很多新的物联网信号就是在传统的无线通信信号的基础上得到的.因此单一地去寻找每一种信号的专家特征不仅低效,而且不具备广泛的适用性.对越来越多的信号进行识别,利用专家特征构建的协同表决模型也会更加复杂.所以信号业务识别的研究在频谱感知甚至是认知无线电频谱动态分配领域都有更加深远的意义. Timothy J. O’Shea团队利用卷积神经网络和卷积自编码器[6-9]对信号IQ数据进行自主的特征提取而非利用传统的专家特征. West等[10]对比了不同深度学习领域的卷积网络模型在信号调制方式识别中的应用.
笔者利用机器学习中的线性回归算法对信号功率谱数据进行拟合处理,提取信号功率谱的拟合因子作为信号特征向量进行统一信号识别,不用再针对不同信号提取不同专家的特征,并且直接应用keras深度学习平台搭建基于多层神经网络的全连接分类模型,将所有被统一标识过的信号特征向量融合在一个输入张量作为输入矩阵进行模型的训练,最后得到表现良好的分类模型,而且结构简单、易懂,且高效.
1 分类模型设计采用深度学习框架keras中的Sequential模型.模型构建的任何操作都可以用Python代码编程实现.
1.1 分类模型结构所有分类模型的构建都是基于softmax回归多分类的多层神经网络,含有2个隐藏层.在信号识别中输入节点的数量等于从信号功率谱数据提取得到的拟合特征向量维度的大小.选取码分多址(CDMA, code division multiple access)上下行、增强型全球移动通信(EGSM, extended global system for mobile)上下行、无线局域网信号(WLAN, wireless local area networks)以及长期演进(LTE, long time evolution)6种信号的功率谱数据作为实验所需频谱数据的样本训练集,所以输出是实验采用的6种实验信号的业务类别编号(1~6).隐藏层1和隐藏层2都设置有1 200个隐藏节点.输出层采用了softmax回归进行多分类,隐藏层节点利用线性整流(RELU, recitified linear unit)激活函数进行激活.分类模型的具体训练与预测原理在2.2节给出.为了防止过拟合在每个隐藏层设置了dropout层,使用的分类模型设置dropout比率为0.2.分类模型采用Adam优化器进行模型参数优化.优化器原理见2.3.
1.2 模型加权系数初始化模型构建的过程中,权重参数wij都由Glorot正态分布(也称作Xavier正态分布初始化)产生. Xavier正态分布均值为0,标准差为sqrt(2/(fan_in + fan_out)),其中fan_in和fan_out是权重张量的扇入扇出(输入和输出单元数).偏置wj0的初始化方式选取全零初始化的方法.
1.3 模型的训练与预测神经网络算法分为前向传播算法和后向传播算法,前向传播进行预测后向传播主要是进行梯度下降优化各层参数.前向传播算法给出模型对输入的预测后,需要后向传播算法对预测进行纠正,并进行模型参数进行优化.首先神经网络会先对D维输入变量进行线性组合,也称为激活[11]
| $ {a_j} = \sum\limits_{i = 1}^D {w_{ji}^{\left( 1 \right)}{x_i}} + w_{j0}^{\left( 1 \right)} $ | (1) |
其中:wji(1)是权重, wj0(1)为偏置.每个激活都会使用一个可微的非线性激活函数h(·)进行变换,可以得到[11]
| $ {z_j} = h\left( {{a_j}} \right) $ | (2) |
h可以选为logistic sigmoid函数或者是双曲正切tanh函数等,函数激活之后再次进行线性组合,得到[11]
| $ {a_k} = \sum\limits_{j = 1}^M {w_{kj}^{\left( 2 \right)}{z_j}} + w_{k0}^{\left( 2 \right)} $ | (3) |
得到了第2层神经网络,对于二分类问题可选取逻辑回归函数
| $ {y_k}\left( {x,w} \right) = \sigma \left( {\sum\limits_{j = 1}^M {w_{kj}^{\left( 2 \right)}h\left( {\sum\limits_{i = 1}^D {w_{ji}^{\left( 1 \right)}{x_i}} + w_{j0}^{\left( 1 \right)}} \right)} + w_{k0}^{\left( 2 \right)}} \right) $ | (4) |
如果是多分类,则最后一层的激活函数为softmax激活函数.式(4)称为前向传播公式,分类模型用此模型进行输入的预测.
神经网络通过反向传播来进行参数的优化,模型训练的总体思路是:对于多分类问题,首先要确定目标变量为{t};对于二分类问题可以把logistic函数得到的0~1的值看成某一类别出现的概率,那么就有[11]
| $ p\left( {t\left| {x,w} \right.} \right) = y{\left( {x,w} \right)^t}{\left\{ {1 - y\left( {x,w} \right)} \right\}^{1 - t}} $ | (5) |
对于分类问题,为了减小过拟合,增强模型的泛化性能,误差函数由负对数似然函数决定:
| $ E\left( w \right) = - \sum\limits_{n = 1}^N {\left\{ {{t_n}{\rm{In}}{y_n} + \left( {1 - {t_n}} \right){\rm{In}}\left( {1 - {y_n}} \right)} \right\}} $ | (6) |
式(6)也被称为交叉熵,而对于多分类问题,同理可得[11]
| $ p\left( {t\left| {x,w} \right.} \right) = \prod\limits_{k = 1}^K {{y_k}{{\left( {x,w} \right)}^{{t_k}}}{{\left[ {1 - {y_k}\left( {x,w} \right)} \right]}^{1 - {t_k}}}} $ | (7) |
| $ E\left( w \right) = - \sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {\left\{ {{t_{nk}}{\rm{In}}{y_{nk}} + \left( {1 - {t_{nk}}} \right){\rm{In}}\left( {1 - {y_{nk}}} \right)} \right\}} } $ | (8) |
神经网络的训练过程就是通过最小化多分类交叉熵误差函数得到最优参数.用反向传播算法[11]进行误差的反向传播来更新权重向量,得到最优的分类模型.
1.4 模型优化器的选择神经网络分类器模型的优化器构建选择Adam(adaptive moment estimation)优化器进行模型参数的优化,基于随机梯度来优化随机目标函数,本质上是带有动量项的RMSprop[11].它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率. Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳.
2 功率谱拟合因子特征提取针对通信信号业务种类识别,提出了一种全新的特征提取方法——功率谱拟合因子特征提取.可以对所有待识别的业务信号进行统一的特征标记,而不需要针对不同信号提取不同专家特征.相比于传统的专家特征(高阶循环谱特征)计算更加简单.
2.1 拟合方法与原理| $ \begin{array}{*{20}{c}} {{\rm{Data}} = \left( {X,Y} \right) = }\\ {\left[ {\left( {{x^{\left( 1 \right)}},{y^{\left( 1 \right)}}} \right),\left( {{x^{\left( 2 \right)}},{y^{\left( 2 \right)}}} \right) \cdots \left( {{x^{\left( m \right)}},{y^{\left( m \right)}}} \right)} \right]} \end{array} $ |
是功率谱训练数据集,x是频率,y是功率(单位:db)假设拟合多项式形式为式(9),向量式为式(10):
| $ h\left( x \right) = {a_0} + {a_1}x + {a_2}{x^2} + \cdots $ | (9) |
| $ {h_\theta } = {\mathit{\boldsymbol{\theta }}^{\rm{T}}}X $ | (10) |
θ是参数集θ =[a0, a1, …],构建一个cost函数为
| $ {\rm{cost}}\left( {X,Y} \right) = {\left( {{h_\theta }\left( X \right) - Y} \right)^2} $ | (11) |
整个数据集上总的代价函数为
| $ \begin{array}{*{20}{c}} {J\left( \theta \right) = \frac{1}{2}\sum\limits_{i = 1}^m {{\rm{cost}}\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right),{y^{\left( i \right)}}} \right)} = }\\ {\frac{1}{2}\sum\limits_{i = 1}^m {{{\left[ {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right]}^2}} } \end{array} $ | (12) |
通过最小化总的代价函数得到最小化时的参数值,即
| $ \theta = \arg \mathop {\min }\limits_\theta \left[ {J\left( \theta \right)} \right] $ | (13) |
得到最好的多项式拟合.最后采用梯度下降法或者导出标准方程[11]进行参数的求解.
2.2 功率谱拟合因子的提取方法采用的实验数据是实际基站采得的功率谱数据.为了统一标识实验数据,拟采用线性回归模型拟合实验数据得到统一拟合因子作为特征进行提取,构建出训练集.
用线性回归模型拟合信号功率谱谱图,
| $ \sum\limits_{i = 0}^n {{w_i}\phi \left( {{x_i}} \right)} = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( x \right) $ | (14) |
其中:W为参数向量是在模型优化中求得的值,Φ(x)为基函数矩阵,可以随意设置,用ϕj=xj的基函数即前文所述的多项式拟合.因为要区分的是不同频段工作的业务信号,有时在实际应用中经常会有频段的迁移.也许同样的信号会在不同的频段上运行,但在这种情况中往往频谱数据的增减趋势没有什么变化.但是因为频谱的迁移拟合直线的截距会有很大的差异,所以直接提取拟合后的全部参数得到必然是错误的答案,很有可能将同一种信号因为采样频段不同或由于干扰造成的频谱迁移而划分成不同的信号类.
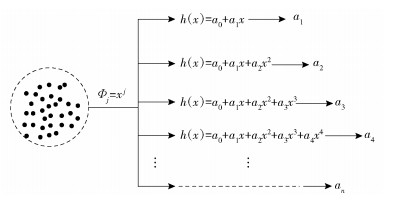
利用线性回归模型(见式(14))分别对功率谱数据进行多项式拟合,然后只提取最高次的系数作为拟合因子提取,提取流程如图 1所示.主要提取方法有如下步骤:1)基于线性回归模型的多项式拟合,选定基函数为k阶多项式a0+a1x+…+akxk对功率谱数据进行拟合;2)由式(10)(11)构造代价函数;3)在整个数据集下构造总的代价函数(式(12)),最小化总代价函数, 得到参数向量θ=[a0, a1, …, ak]; 4)提取最高阶拟合因子ak.
|
图 1 拟合因子正确提取方法示意图 |
原始的训练数据集[(X, Y), label]是由频谱数据和相应的标签构成.通过2.2节的方法对原始频谱数据进行拟合因子特征提取,可以提取多个拟合因子构成特征向量feature=[a1, a2, …, ak];然后可以构建新的特征集[feature, label],每一组(X, Y)频谱数据对应一个特征提取后的feature向量;最后利用[feature, label]特征集作为分类器的输入,进行有监督的训练.
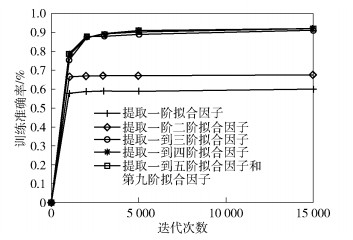
3 数值结果构建分类模型之前,按照2.3节所述先对原始的功率谱数据进行拟合因子特征提取,得到特征向量(feature=[a0, a1, …, an]),将原始的数据集[(X, Y), label]变成训练数据集[feature, label]的形式作为输入进行分类训练.分类模型的输出就是对输入预测为某一类别的概率.具体的分类效果如图 2所示.
|
图 2 提取不同拟合因子个数的分类模型训练准确率 |
随着提取拟合因子阶数的升高,准确率也进一步提升.因为完全从频谱形状出发进行特征提取,所以提取的谱形状因子越多,正确率也会有提升.可见只进行一次特征提取,得到模型正确率较低,只有60%左右,不能完全识别信号,说明线性因子不足以对频谱波形进行标识;之后在一阶拟合因子提取的基础上又增加了二阶拟合因子的提取,分类模型正确率有了进一步提升,但效果仍不够好;之后又增加了三次因子、四次因子、五次因子、九次因子,发现分类结果的正确率已经达到90%以上,且收敛速度更快.但是提取的三次以上因子的准确率基本达到同一种程度[11].最后选定提取6个拟合因子(一次、二次、三次、四次、五次、九次)作为特征向量进行试验观测.由图 3可见,训练次数达到10万次以上会得到更好效果的分类器模型准确率基本在97%左右,但是随着训练次数的增长,模型性能提升也变得越来越平缓.

|
图 3 提取6个拟合因子分类模型训练准确率 |
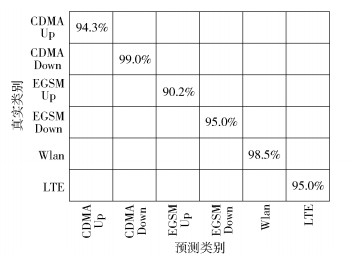
在测试集上对模型进行测试,用模糊矩阵描述模型在测试数据上的表现.如图 4所示,针对6种实验信号都达到了90%以上的识别准确率,除了EGSM上行信号,其他信号都基本可以达到95%的识别准确率.
|
图 4 测试数据的模糊矩阵 |
与传统调制识别的方法相比,例如在基于高阶循环谱特征提取的调制识别中[2],分类器可以整体获得90%以上的准确率,但仍有个别识别效果不好的情况(低于80%).可是在基于笔者提出的方法中对所有实验信号都可以达到90%以上的准确率,而且不用针对不同类别提取不同的专家特征,只需提取功率谱拟合因子就可以对所有类别进行特征提取.
4 结束语通过大量的实验对不同业务信号的功率谱数据提取了多项式拟合因子,对所有欲识别信号业务给出了一个统一的特征标识,并对特征进行了分类模型构建及分析.通过对信号功率谱拟合因子的提取和建模分析,得到了非常好的训练和预测效果.总体的信号业务分类流程总结如下:1)从30 MHz~3 GHz的信号功率谱数据中截取相应业务信号的功率谱数据构建原始数据集[(X, Y), label];2)对式(1)中的原始数据进行功率谱拟合因子特征提取,得到特征向量feature=[a1, a2, …, ak],构建分类所需的训练数据集[feature, label];3)按照第2节所述构建分类模型;4)将式(2)构建好的训练数据集作为分类模型的输入,进行有监督的训练;5)对模型参数进行优化调试,得到效果良好的分类模型.
与传统的信号识别方法相比,所提方法主要的优点如下:1)可以直接得到信号业务种类的识别,而不仅仅停留在信号调制方式的识别;2)提取信号功率谱的拟合因子作为特征,标记所有业务信号,而不需要再针对不同信号提取不同的专家特征;3)相比于传统的循环谱特征提取,功率谱拟合因子的提取计算更加简单.
| [1] |
吴月娴, 葛临东, 许志勇. 常用数字调制信号识别的一种新方法[J]. 电子学报, 2007, 35(4): 782–785.
Wu Yuexian, Ge Lindong, Xu Zhiyong. A new method for identifying commonly used digital modulation signals[J]. Acta Electronic Journal, 2007, 35(4): 782–785. |
| [2] |
朱雷, 程汉文, 吴乐南. 利用循环谱和参数统计的数字调制信号识别[J]. 应用科学学报, 2009, 27(2): 137–143.
Zhu Lei, Cheng Hanwen, Wu Lenan. Recognition of digital modulation signals using cyclic spectrum and parametric statistics[J]. Journal of Applied Sciences, 2009, 27(2): 137–143. |
| [3] |
张晓, 王金龙, 吴启晖. 认知无线电中一种基于循环谱的能量检测算法[J]. 电路与系统学报, 2010, 15(3): 75–80.
Zhang Xiao, Wang Jinlong, Wu Qihui. An energy detection algorithm based on cyclic spectrum in cognitive radio[J]. Journal of Circuits and Systems, 2010, 15(3): 75–80. |
| [4] |
崔丽, 王金龙, 吴启晖, 等. 认知无线电中基于信息简约的最大似然协同频谱感知算法[J]. 电子与信息学报, 2009, 31(9): 2177–2182.
Cui Li, Wang Jinlong, Wu Qihui, et al. The maximum likelihood cooperative spectral sensing algorithm based on information simplicity incognitive radio[J]. Journal of Electronics & Information Technology, 2009, 31(9): 2177–2182. |
| [5] |
辛建芳, 张立毅, 魏瑾, 等. 基于高阶累积量的数字调制信号识别[C]//中国通信学会学术年会. 中国通信学会第五届学术年会论文集. 南京: 中国通信学会, 2008: 462-466.
Xin Jianfang, Zhang Liyi, Wei Jin, et al. Digitalmodulation signal recognition based on high order cumulant[C]//Annual Conference of China Communications Society. The 5th Academic Conference Proceedings of China Communications Scoiety. Nanjing: China Communications Association, 2008: 462-466. |
| [6] | O'Shea T J, Corgan J, Clancy T C. Convolutional radio modulation recognition networks[C]//International Conference on Engineering Applications of Neural Networks. [S. l. ]: Springer International Publishing, 2016: 213-226. |
| [7] | O'Shea T J, Corgan J, Clancy T C. Unsupervised representation learning of structured radio communication signals[C]//First International Workshop on Sensing, Processing and Learning for Intelligent Machines. Aalborg, Denmark: IEEE, 2016: 1-5. |
| [8] | O'Shea T J, West N, Vondal M, et al. Semi-supervised radio signal identification[C]//International Conference on Advanced Communication Technology. Bougp yeoug, South Korea: IEEE, 2017: 33-38. |
| [9] | O'Shea T J, Hoydis J. An introduction to machine learning communications systems[EB/OL]. 2017. http://arxiv.org/abs/1702.00832. |
| [10] | West N E, O'Shea T J. Deep architectures for modulation recognition[C]//IEEE International Symposium on Dynamic Spectrum Access Networks. [S. l. ]: IEEE, 2017: 1-6. |
| [11] | Anzai Y. Pattern recognition and machine learning[M]. Singapore: Springer, 2006: 225-247. |


