2. 鲁东大学 资产处, 山东 烟台 264025
为提高证据冲突度量和融合结果的准确性,提出一种基于证据排序融合的局部冲突信息再分配算法.该算法首先基于证据距离和冲突系数共同度量证据冲突,在此基础上对证据融合顺序进行优化,并对不同证据中不同焦元的冲突度量算法进行改进.进一步,在对证据进行依序融合过程中,将新的证据以及焦元冲突度量结果应用于对局部冲突信息进行再分配.与已有相关算法进行的理论和应用对比分析结果表明,所提算法的证据融合效果更加稳定、可靠.
2. Assets Department, Ludong University, Shandong Yantai 264025, China
In order to improve the accuracy of evidence conflict measure and evidence fusion, a local conflict information redistribution algorithm based on evidence ranking fusion is proposed. The evidence conflict is firstly measured based on the evidence distance and the conflict coefficient in the new algorithm, and on this basis, the order of evidence fusion is optimized and the conflict measure algorithm of different focal elements in different pieces of evidence is improved. Further, during the sequential fusion of evidence, the new conflict measure results of the evidence and the focal element are applied to the redistribution of local conflict information. The performances of the new algorithm and the related algorithms are comparatively analyzed in theory and application, and the results show that the evidence fusion effect of the new algorithm is more stable and reliable.
近年来,Dempster-Shafter(D-S)证据理论在目标识别、故障诊断以及智能决策等诸多领域均具有广泛应用,但其在处理高冲突证据时常会出现反直观现象.为此,学者们主要从对冲突证据进行预处理和针对D-S证据组合规则进行修正两方面对该问题展开研究[1].目前,针对冲突证据的预处理算法多是先对证据进行冲突度量,确定证据权系数,而后对所得加权证据利用D-S组合规则进行自身融合[2-3];对D-S组合规则的修正算法,则主要是针对算法模型进行推广和对冲突信息在相应范围内进行重新分配[4-6].以上2类改进算法的关键均是要对证据冲突进行有效度量.目前常用的冲突度量参数包括冲突系数、证据距离、信息熵、相似度以及虚假度等,但研究结果表明,单一的冲突度量参数均存在某些方面的不足,无法独立完成对各类冲突证据的有效度量.
通过综合分析冲突系数和Jousselme证据距离2个冲突度量参数各自的优势与不足,笔者将二者进行综合,应用于解决单子集焦元证据之间的冲突度量问题.在此基础上,进一步通过优化证据组合顺序,对焦元可信度计算式进行改进,在不同程度上提高了对目标的正确识别概率.
1 证据组合 1.1 D-S证据组合规则设非空集合Θ={θ1, θ2, …, θn}是一辨识框架,Θ的幂集2Θ构成命题集合. m是2Θ到[0, 1]区间的一个映射,满足m(∅)=0和
设mj(j=1, 2, …, J)是J个相互独立的基本概率分配函数,其D-S证据组合规则为
| $ \begin{array}{*{20}{c}} {m\left( X \right) = }\\ {\left\{ \begin{array}{l} \frac{{\sum\limits_{{A_i} \cap {A_j} \cap \cdots \cap {A_l} = X} {\left[ {{m_1}\left( {{A_i}} \right){m_2}\left( {{A_j}} \right) \cdots {m_J}\left( {{A_l}} \right)} \right]} }}{{1 - k}},\;\;\;\;X = \emptyset \\ 0,\;\;\;\;X = \emptyset \end{array} \right.} \end{array} $ | (1) |
| $ k = \sum\limits_{{A_i} \cap {A_j} \cap \cdots \cap {A_l} = \emptyset } {\left[ {{m_1}\left( {{A_i}} \right){m_2}\left( {{A_j}} \right) \cdots {m_J}\left( {{A_l}} \right)} \right]} $ | (2) |
称k为冲突系数或不一致因子.
1.2 证据冲突度量已有研究表明,传统冲突系数不能很好度量包含非单子集焦元证据之间的冲突,而一些证据距离和相似度函数也存在不能很好刻画概率赋值较分散证据之间的真实冲突问题.为提高对证据的冲突度量效果,除了应考虑对冲突证据进行分类度量外,还应根据不同度量参数的特点对其进行综合应用,以期发挥不同度量参数各自的优势,避免其不足.
与证据冲突度量结果密切相关的另一方面是证据可信度的计算公式.在采用同一参数度量证据冲突的前提下,证据可信度的计算式不同,冲突度量结果会有很大差别.例如,有如下证据:
1) m1(A)=0.45, m1(B)=0.50, m1(C)=0.05
2) m2(A)=0.10, m2(B)=0.70, m2(C)=0.20
3) m3(A)=0.70, m3(B)=0.20, m3(C)=0.10
4) m4(A)=0.40, m4(B)=0.30, m4(C)=0.30
对上述证据采用文献[2]算法的融合结果为m(A)=0.49, m(B)=0.50, m(C)=0.01.在文献[2]的算法中,证据可信度的计算式为c(mi)=s(mi)/
显然,采用不同的证据可信度计算式所得目标识别结论不同.不难看出,与求和型计算式相比,求积型计算式能够对高冲突证据赋予较低的权重,有利于减少冲突证据对证据融合结果的影响.
1.3 冲突证据的组合目前,多数改进证据融合算法采用类似文献[2]的算法流程,即将待融合J条证据的加权证据体利用D-S组合规则进行自身融合J-1次,得到最终证据组合结果.该类算法的优点是算法仍满足可结合特性,不足是证据组合结果的准确性完全依赖于对证据的冲突度量结果.
曹浩等[5]基于Jousselme证据距离度量证据冲突,并将冲突度量结果用于对两两证据组合过程中形成的局部二维冲突信息进行再分配,在一定组合顺序下能够提高证据融合精度.但由于其不满足结合律,证据组合结果随证据组合顺序变化而有所改变,稳定性较低.为避免该不足,周莉等[6]将文献[5]算法中的局部二维冲突信息再分配算法推广至多维的情形,即将多条证据共同合成过程中形成的部分多维冲突组合所含不一致信息直接进行加权再分配.如此,不仅可以提高多维冲突信息的利用率,且可以避免证据组合顺序对融合结果的影响,提高证据组合结果的准确性.该算法的不足是随证据维数的增高其计算负担较重,且收敛速度较慢.
为发挥上述2种算法的优势,避免其不足,笔者考虑在进一步提高证据冲突度量算法准确性的基础上,利用改进的冲突度量结果对多证据两两组合顺序进行优化,并对不同证据中各焦元的权重计算式进行改进,以期进一步提高对局部冲突信息再分配的精度,进而提高证据组合结果的可靠性.
2 改进的局部冲突信息再分配算法如果将基于Jousselme证据距离度量证据可信度的计算式与基于冲突系数计算证据可信度的公式对应相乘,则对于证据概率赋值相对较分散的证据来说,冲突系数能够通过对局部冲突信息的准确度量弥补此时基于Jousselme证据距离度量证据冲突度取值偏低的不足;而对于接近相似的2条证据,将基于Jousselme证据距离的冲突度量结果与基于冲突系数的冲突度量结果相乘后再归一化,能起到很好的折中效果.因此,利用上述2个参数共同度量证据冲突具有很好的优势互补作用.
2.1 新的证据冲突度量算法设mi(i=1, 2, …, J)是J条两两相互独立的待融合证据.根据式(2),证据mi和mj之间的冲突系数可表示为
| $ {k_{ij}} = \sum\limits_{\begin{array}{*{20}{c}} {r,t}\\ {{A_r} \cap {B_t} = \emptyset } \end{array}} {{m_i}\left( {{A_r}} \right){m_j}\left( {{B_t}} \right)} $ | (3) |
则证据mi被其他证据支持的度量可描述为
| $ s_i^k = \prod\limits_{j = 1,i \ne j}^J {\left( {1 - {k_{ij}}} \right)} ,\forall i,j = 1,2, \cdots ,J $ | (4) |
而证据mi基于冲突系数的可信度表示为
| $ c_i^k = \frac{{s_i^k}}{{\sum\limits_{j = 1}^J {s_j^k} }},j = 1,2, \cdots ,J $ | (5) |
另外,证据mi和mj之间的Jousselme证据距离表示为
| $ \begin{array}{*{20}{c}} {{d_{ij}} = \frac{1}{{\sqrt 2 }}{{\left[ {{{\left( {{\mathit{\boldsymbol{m}}_i} - {\mathit{\boldsymbol{m}}_j}} \right)}^{\rm{T}}}\mathit{\boldsymbol{D}}\left( {{\mathit{\boldsymbol{m}}_i} - {\mathit{\boldsymbol{m}}_j}} \right)} \right]}^{1/2}}}\\ {\forall i,j = 1,2, \cdots ,J,{j_1} \ne {j_2}} \end{array} $ | (6) |
其中D(A, B)=|A∩B|/|A∪B|.
故证据mi基于Jousselme证据距离的可信度可描述为
| $ c_i^d = \frac{{s_i^d}}{{\sum\limits_{j = 1}^J {s_j^d} }},j = 1,2, \cdots ,J $ | (7) |
其中
| $ s_i^d = \prod\limits_{j = 1,i \ne j}^J {\left( {1 - {d_{ij}}} \right)} ,\forall i,j = 1,2, \cdots ,J $ | (8) |
于是,证据mi基于冲突系数和Jousselme证据距离的融合可信度可表示为
| $ c_i^f = \frac{{c_i^ks_i^d}}{{\sum\limits_{j = 1}^J {c_i^ks_j^d} }},j = 1,2, \cdots ,J $ | (9) |
1) 改进的焦元可信度计算式
令mw(Aj)表示待融合J条证据中焦元Aj概率赋值的加权平均值,即
| $ {m_w}\left( {{A_j}} \right) = \sum\limits_{i = 1}^J {c_i^f{m_i}\left( {{A_j}} \right)} $ | (10) |
则mi(Aj)与mw(Aj)之间的距离可表示为
| $ {f_d}\left[ {{m_i}\left( {{A_j}} \right)} \right] = \left| {{m_i}\left( {{A_j}} \right) - {m_w}\left( {{A_j}} \right)} \right| $ | (11) |
而mi(Aj)与mw(Aj)之间的相似性度量可描述为
| $ \begin{array}{*{20}{c}} {{f_s}\left[ {{m_i}\left( {{A_j}} \right)} \right] = 2{m_i}\left( {{A_j}} \right){m_w}\left( {{A_j}} \right)/{{\left[ {{m_i}\left( {{A_j}} \right)} \right]}^2} + }\\ {{{\left[ {{m_w}\left( {{A_j}} \right)} \right]}^2}} \end{array} $ | (12) |
为了更好地体现mi(Aj)本身所具有的可信程度,曹洁等[5]将证据mi中焦元Aj的信任度修正为{1-fd[mi(Aj)]}fs[mi(Aj)].与式(12)相比,修正后的焦元信任度能够更好地反映证据mi中焦元Aj的概率赋值的可信程度.但fd[mi(Aj)]表示的是mi(Aj)与mw(Aj)之间的绝对距离差,还不能很好地刻画该距离在概率赋值的加权平均值中所占比例,因此,笔者考虑利用相对距离差来描述mi中焦元Aj的概率赋值与其加权均值之间的关系,具体将二者之间的相对距离差描述为
| $ {f_{rd}}\left[ {{m_i}\left( {{A_j}} \right)} \right] = \left\{ \begin{array}{l} 1,\;\;\;\;\left| {{m_i}\left( {{A_j}} \right) - {m_w}\left( {{A_j}} \right)} \right| > {m_w}\left( {{A_j}} \right)\\ \left| {{m_i}\left( {{A_j}} \right) - {m_w}\left( {{A_j}} \right)} \right|/{m_w}\left( {{A_j}} \right),\;\;\;\;其他 \end{array} \right. $ | (13) |
于是,mi(Aj)与mw(Aj)之间的融合信任度函数可表示为
| $ f_s^f\left[ {{m_i}\left( {{A_j}} \right)} \right] = \frac{{1 - {f_{rd}}\left[ {{m_i}\left( {{A_j}} \right)} \right]}}{{\sum\limits_{i = 1}^J {\left\{ {1 - {f_{rd}}\left[ {{m_i}\left( {{A_j}} \right)} \right]} \right\}} }}\frac{{{f_s}\left[ {{m_i}\left( {{A_j}} \right)} \right]}}{{\sum\limits_{i = 1}^J {{f_s}\left[ {{m_i}\left( {{A_j}} \right)} \right]} }} $ | (14) |
进一步,为了强化证据权重在冲突信息分配中的作用,定义mi中焦元Aj的可信度为
| $ {f_c}\left[ {{m_i}\left( {{A_j}} \right)} \right] = \frac{{c_i^ff_s^f\left[ {{m_i}\left( {{A_j}} \right)} \right]}}{{\sum\limits_{i = 1}^J {\sum\limits_{j = 1}^n {c_i^ff_s^f\left[ {{m_i}\left( {{A_j}} \right)} \right]} } }} $ | (15) |
2) 改进证据组合顺序的多证据融合算法
在文献[5]算法中,将冲突度较高的证据排在组合顺序的末端会严重影响证据组合结果的可靠性.因此,笔者按各证据基于冲突系数和证据距离的融合可信度取值自小至大的顺序对多证据进行排序,并依序对其进行两两融合.
依据式(15),证据mi和mj融合时焦元Au的概率分配值可表示为
| $ \begin{array}{*{20}{c}} {m\left( {{A_u}} \right) = {m_ \cap }\left( {{A_u}} \right) + }\\ {\sum\limits_{{A_u} \cap {A_v} = \emptyset } {\frac{{{f_c}\left[ {{m_i}\left( {{A_u}} \right)} \right]{m_i}\left( {{A_u}} \right){m_i}\left( {{A_u}} \right){m_j}\left( {{A_v}} \right)}}{{{f_c}\left[ {{m_i}\left( {{A_u}} \right)} \right]{m_i}\left( {{A_u}} \right) + {f_c}\left[ {{m_j}\left( {{A_v}} \right)} \right]{m_j}\left( {{A_v}} \right)}}} + }\\ {\sum\limits_{{A_u} \cap {A_v} = \emptyset } {\frac{{{f_c}\left[ {{m_j}\left( {{A_u}} \right)} \right]{m_j}\left( {{A_u}} \right){m_i}\left( {{A_v}} \right){m_j}\left( {{A_u}} \right)}}{{{f_c}\left[ {{m_j}\left( {{A_u}} \right)} \right]{m_j}\left( {{A_u}} \right) + {f_c}\left[ {{m_i}\left( {{A_v}} \right)} \right]{m_i}\left( {{A_v}} \right)}}} } \end{array} $ | (16) |
其中u, v=1, 2, …, n, u≠v,n为证据中焦元的个数.
3 算例及仿真分析例1 识别框架为Θ={A, B, C},4条证据分别为
1) m1:m1(A)=0.60, m1(B)=0.30, m1(C)=0.10
2) m2:m2(A)=0.47, m2(B)=0.43, m2(C)=0.10
3) m3:m3(A)=0.50, m3(B)=0.40, m3(C)=0.10
4) m4:m4(A)=0.20, m4(B)=0.70, m4(C)=0.10
对上述证据采用相关算法的证据合成结果如表 1所示.其中,加法加权和乘法加权的结果分别指利用1.2节中所介绍求和型和求积型计算式计算证据可信度所得加权证据;邓算法即邓勇等[2]所提算法;宋算法是宋亚飞等[3]所提算法;直接融合算法指在文献[6]算法的基础上,对所有多维冲突信息均进行加权再分配的改进算法,其中加法和乘法分别指采用基于Jousselme证据距离度量证据冲突的求和型和求积型计算式计算证据可信度的对应算法;曹算法指曹洁等[5]所提算法;新算法即笔者所提改进算法.
|
|
表 1 相关算法的证据合成结果 |
该例中,前3条证据的概率赋值均偏向于焦元A,只有第4条证据偏向于焦元B.因此,第4条证据很可能是一条冲突证据.
由表 1可知,除了D-S组合规则和曹算法外,其他算法的证据组合结果均为焦元A,与直观分析结果相符.该例中,焦元A和焦元B在各证据中概率赋值的平均加权相加结果相差不大,且由加法加权结果可知,加法加权证据中焦元A的概率赋值0.453仅比焦元B的概率赋值0.447高出0.006.因此,该例属于高冲突证据.由于D-S组合规则不适用于处理高冲突证据,且没有考虑到证据权重,其证据合成结果有失准确.而该例中证据的自然排序对曹算法不是很有利,因此其证据组合结果相对较差.其中,新算法的正确目标识别概率比曹算法对应结果高出0.13个点.
另外,对比邓算法和宋算法可知, 邓算法优于宋算法.说明文献[3]中融合虚假度和证据余弦距离度量证据冲突的算法, 并不是在任何时候都优于只利用证据距离度量证据冲突的相关算法.分别对比加法加权和乘法加权以及直接融合(加法)和直接融合(乘法)的证据组合结果可以看出,乘法加权算法均对应优于加法加权算法,该结论与在1.2节中对证据支持度计算式分析结果相一致.
例2 设有7部传感器同时对某空域3个未知飞行物进行观测识别,识别框架Θ={A, B, C},其中A为战斗机,B和C均为民用客机. 3个目标A、B、C均在与传感器观测系统间距100 km处相对飞行,3个目标的飞行速度均为1 000 m/s.传感器1正确判断3个目标的飞行器种类的置信度始终分别为0.5、0.4、0.1,传感器2正确判断3个目标的飞行器种类的置信度始终分别为0.01、0.49、0.5.传感器3、4、5、6、7在100 km处对目标A机型正确判断的置信度均为0.25,在10 km处对A机进行正确识别的可能性大小均为0.7,该期间内,其对战斗机的判别准确度与其实时间距成反比;在整个过程中,除干扰阶段外,传感器3、4、5、6、7对B机类型进行正确判断的置信度始终为0.2.
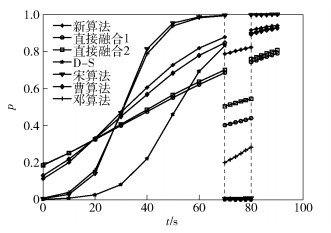
在与目标相距30~20 km处,传感器6和7受到干扰,正确判断A、B机类型的可能性大小为0. 图 1和图 2所示分别为在上述仿真环境下,采用相关算法的证据组合结果,其中直接融合1表示直接融合(加法),直接融合2表示直接融合(乘法).
|
图 1 识别A为战斗机的概率 |

|
图 2 识别B为战斗机的概率 |
由图 1可以看出,在探测环境相对较差,但没有强干扰的情况下,邓算法和宋算法均能取得较好的证据合成效果,且其收敛速度较快.原因是它们均间接利用了经典D-S组合规则,该规则的优点就是具有较快的聚焦速度.但D-S组合规则由于没有对证据进行加权处理,其目标识别结果不理想,但仍能随着获取信息的增多越来越准确地识别出目标,且收敛速度较快.对比图 1和图 2可知,在强干扰阶段,只有新算法和直接融合2算法能够准确识别出目标,且与直接融合2算法相比,新算法的正确目标识别概率提高了约0.14个点,表现出较强的抗干扰特性,而其余算法均错误地将目标B识别为战斗机.
4 结束语笔者对证据冲突度量算法和局部冲突信息再分配算法进行研究,并给出了相应的改进算法.针对单子集焦元冲突证据融合问题,提出利用Jousselme证据距离和冲突系数共同度量证据冲突的改进算法.理论分析和实验结果表明,新的冲突度量算法不仅能避免单参数度量算法存在的不足,且能通过提高局部冲突度量结果的准确性赋给偏好的差异证据较高的权重,提高证据冲突度量结果的可靠性.
在改进冲突度量算法的基础上,对证据及焦元可信度计算式进行了改进,从而改进了局部冲突信息再分配算法,在不同程度上提高了局部冲突信息再分配的精度.由图 1和图 2可以看出,与具有较好稳定性的直接融合算法相比,新算法始终具有较准确的目标识别结果和较高的正确目标识别概率;并且,由于新算法是对多证据进行两两组合运算,其计算量远远低于对高维证据进行直接融合的运算量.如何通过对多参数进行综合利用,有效度量含有非单子集焦元证据之间的冲突,是后续需要进一步深入研究的一项课题.
| [1] | Shafer G. A mathematical theory of evidence turns 40[J]. International Journal of Approximate Reasoning, 2016, 79: 7–25. doi: 10.1016/j.ijar.2016.07.009 |
| [2] |
邓勇, 施文康, 朱振福. 一种有效处理冲突证据的组合方法[J]. 红外与毫米波学报, 2004, 23(1): 27–32.
Deng Yong, Shi Wenkang, Zhu Zhenfu. Efficient combination approach of conflict evidence[J]. Journal of Infrared and Millimeter Waves, 2004, 23(1): 27–32. |
| [3] |
宋亚飞, 王晓丹, 雷蕾, 等. 基于信任度和虚假度的证据组合方法[J]. 通信学报, 2015, 36(5): 98–103.
Song Yafei, Wang Xiaodan, Lei Lei, et al. Evidence combination based on the degree of credibility and falsity[J]. Journal on Communications, 2015, 36(5): 98–103. |
| [4] | Deng Yong. Generalized evidence theory[J]. Applied Intelligence, 2015, 43(3): 530–543. doi: 10.1007/s10489-015-0661-2 |
| [5] |
曹洁, 郭雷雷. 一种基于局部冲突分配的证据组合规则[J]. 计算机应用研究, 2013, 30(7): 2033–2035.
Cao Jie, Guo Leilei. Evidence combination rule based on local conflict distribution strategy[J]. Application Research of Computers, 2013, 30(7): 2033–2035. |
| [6] |
周莉, 唐文静, 郭伟震. 一种改进D-S证据组合规矩的目标识别算法[J]. 北京邮电大学学报, 2016, 36(5): 47–50.
Zhou Li, Tang Wenjing, Guo Weizhen. Target-recognition algorithm based on improved D-S evidence combination rule[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 36(5): 47–50. |


