2. 国网吉林省电力有限公司信息通信公司技术发展部, 长春 130000
针对多源供电的无线异构网络,综合考虑可再生能源的产能速率、传统能源的分时电价和用户间的公平性对于用户选择的影响,提出了2个基于能源代价的用户选择算法,将用户选择分为边缘用户分配和确定服务用户2个阶段,得到了更加均衡的负载分布.根据能量损耗、能源代价与公平性之间的关系,构造了直接法和间接法中2种指数型效用函数.仿真结果表明,直接法和间接法均可明显降低基站系统能量损耗和能源代价,而直接法相当于在间接法的指数型效用函数的底数前增加了一个随传统能源电价和可再生能源速率自适应变化的价格因子,因而可以在降低能源代价的条件下减少基站系统能量损耗.
2. Technology Development Department, China of Limited Company of Jilin Province Power Communication Company, Changchun 130000, China
In the heterogeneous network based on multi-source power supply, two user selection algorithms based on energy cost were proposed considering the influences of supply rate of renewable energy, peak-valley time-of-use tariff strategy of the traditional energy and the fairness among users. The processes of user selection can be divided into two stages which are allocating the users on the cell edge and determining the users who can get service, and a balanced load distribution was obtained. According to the relationships among power consumption, energy cost and the fairness among users, two exponential utility functions were constructed in the direct and the indirect method, respectively. Simulations show that the direct and indirect method can significantly reduce the power consumption and energy cost of base station system. Compared with the indirect method, the direct method employs an adaptive price factor, which changes with the electricity price of traditional price and the supply rate of renewable energy. Thus, it can reduce the power consumption at a lower level of energy cost.
无线异构组网是公认的5G通信系统架构,实现了无线资源“量”的大幅增加,配合合理的用户分配策略可进一步提高网络性能.而当用户数大于基站的负载能力时,则需要通过用户选择确定基站的服务用户. Lin Yan等[1]在用户选择过程中考虑了公平性指标,避免了部分处于较差信道的用户长时间得不到服务. Zhang等[2]提出了“拓扑势”的概念,在兼顾公平性的前提下,优化了时间域上的资源分配.上述用户选择技术未从能量域关注资源分配问题,忽略了能量损耗造成的经济代价.为此,笔者构建了综合能量供给模型,综合考虑了可再生能源的波动性与不确定性、传统能源的分时电价策略与用户间的公平性,提出了2个异构网络中的用户选择算法.所提算法将用户选择分为分配边缘用户和确定服务用户2个阶段,并构造了能源经济成本的“拓扑势”指数型效用函数,在保证公平性的同时,降低了能量损耗和经济成本.
1 系统模型考虑由1个宏基站和多个微基站构成的异构网络下行链路系统模型.宏基站形成1个宏小区,在宏小区覆盖范围内部署多个微基站.每个基站覆盖范围内用户随机分布,且每个用户只能由1个基站为其提供服务.宏基站具有MM根发射天线,微基站具有MP根发射天线,用户终端采用1根天线.
假设传输信道H=[hm, n, 1, …, hm, n, k, …, hm, n, Kn]已知,其中hm, n, k表示小区m到小区n中用户k之间的信道矢量. Kn表示小区n的当前用户数.其中,n∈N,N={1, 2, …, N}.不妨设n=1代表宏小区,n≠1代表微小区.则小区n中用户k的接收信号为
| $ \begin{array}{*{20}{c}} {{y_{n,k}} = {h_{n,n,k}}{x_{n,n,k}} + \underbrace {{h_{n,n,k}}\sum\limits_{l \ne k}^{{K_n}} {{x_{n,n,l}}} }_{多用户干扰} + }\\ {\underbrace {\sum\limits_{m \in N,m \ne n} {\sum\limits_{i = 1}^{{K_n}} {{h_{m,n,i}}{x_{m,n,i}}} } }_{小区间干扰} + {n_{n,k}}} \end{array} $ | (1) |
其中: hn, n, k为小区n到小区n中用户k之间的传输信道矢量,xn, n, k为基站n到小区n中用户k的预编码信号,nn, k是传输过程中受到的高斯白噪声.
假设发射端已知hn, n, k, ∀n∈N,k∈Kn.利用迫零预编码消除多用户干扰,预编码矩阵V=HH(HHH)-1,即xn, n, k=vn, n, ksn, n, k,使得hn, n, k=vn, n, l=0(∀l∈Kn, l≠k).那么经预编码处理后,小区n中用户k的信干噪比r可以表示为
| $ {r_{n,k}} = \frac{{{P_n}{{\left\| {{h_{n,n,k}}{x_{n,n,k}}} \right\|}^2}}}{{{P_m}\sum\limits_{m \in N,m \ne n} {\sum\limits_{i = 1}^{{K_n}} {{{\left\| {{h_{m,n,i}}} \right\|}^2}{{\left\| {{x_{m,n,i}}} \right\|}^2}} } + {\sigma ^2}}} $ | (2) |
其中Pn表示基站n的发射功率.分母中,第1项是用户接收到的小区间干扰,σ2为噪声功率.
为简化分析步骤,假设上述系统由1个宏基站和2个微基站组成,且所有基站处于激活状态.宏基站可由采用传统能源的电网、太阳能和风能供给电量,而微基站1由电网及太阳能供给能源,微基站2由电网和风能提供能量.基站的能量损耗由固有损耗Pfix和发射功耗P两部分组成,可表示为
| $ {P_{{\rm{BS}}}} = {P_{{\rm{fix}}}} + \eta P $ | (3) |
其中:η为固定常数,代表增加单位发射功率时基站能耗的增量.那么基站系统总能耗为
| $ {P_{\rm{s}}} = \sum\limits_{t \in \mathit{\Gamma }} {\sum\limits_{n \in N} {{P_{{\rm{BS}}n,t}}} } $ | (4) |
由于可再生能源的产能周期为15 min,故将1 d的时间划分为96个时隙,记为t∈G{1, 2, …, T},时隙宽度ωt=15 min.根据Elia机构统计的数据可知[3],太阳能产能速率近似服从正态分布,其表达式为
| $ {E_1}\left( t \right) = 0.7\exp \left( { - \frac{{{{\left( {t - 48} \right)}^2}}}{{81}}} \right) $ | (5) |
风能的产能速率固定为
| $ {E_2}\left( t \right) = 0.6 $ | (6) |
电网采用分时电价策略,记为q1t.可再生能源的电价固定为q2,且采用负价格形式,即q2<0[4].那么基站系统的能源代价可表示为
| $ \begin{array}{*{20}{c}} {C = \sum\limits_{t \in \mathit{G}} {\sum\limits_{n \in N} {\left( {{q_{1t}}{P_{{\rm{BS}}n,t}} + {q_2}{E_{n,t}}} \right)} } = }\\ {\sum\limits_{t \in \mathit{G}} {\sum\limits_{n \in N} {\left( {{q_{1t}}{P_{{\rm{BS}}n,t}} + {q_2}\left( {{E_{1n,t}} + {E_{2n,t}}} \right)} \right)} } } \end{array} $ | (7) |
在综合考虑能量损耗和公平性的基础上,进一步研究了两者与能源代价间的关系,提出了2个基于能源代价的用户选择算法——直接法和间接法.其中,直接法将能源代价当作直接优化目标,而间接法则是通过降低基站系统能量损耗减少能源代价.用户间公平性的提高,必然造成能量损耗的增加,提高公平性与降低能量损耗是2个“相悖”的优化目标,因此采用P和1/J的形式构成目标函数.而当达到最公平(用户依次享受到服务,即轮询机制)时,基站系统的能量损耗趋近于某一固定值,而由于公平性采用分式1/J的形式,故构造了指数型效用函数.根据博弈论的思想,能量损耗P与用户公平性J相互制衡,最终存在均衡点.类似地,构造了能源代价与公平性的指数型效用函数.
此外,根据微小区内用户接入信号强弱,将小区内用户分为中心用户和边缘用户[5].同时兼顾了边缘用户的分配与服务用户选择2个方面,将用户选择分为2个阶段;其次,在基站系统中,单位能量价格一定的情况下,亦可通过降低系统能量损耗的方式降低系统的总能源代价.为此,在比例公平调度(PFS,proportional fair scheduling)算法的基础上,分别以能源代价和能量损耗为自变量构造了相应的指数型效用函数,在考虑用户间公平性的同时,兼顾了能量损耗和能源代价的问题.
2.1 间接法间接法通过降低能量损耗,减少基站系统能源代价,利用能量损耗P与公平性J构造了函数U1,
| $ {U_1}\left( {t,k} \right) = {P_k}{\left( t \right)^{\frac{1}{{{J_k}\left( t \right)}}}} $ | (8) |
其中
| $ {J_k}\left( t \right) = \frac{{{R_k}\left( t \right)}}{{{T_k}\left( t \right)}} $ | (9) |
式(8)为定义的能量域“拓扑势”函数,用以描述用户选择过程中相互联系、相互影响的能量损耗和公平性.其中Pk(t)表示t时隙选择用户k对应的基站能量损耗,Jk(t)表示t时隙用户k的公平性.式(9)定义Jk(t)为用户k在当前时隙的传输速率Rk(t)与过去tc时间内该用户的传输速率Tk(t)的比值,并以此衡量其等效信道质量,兼顾了用户当前的服务质量与其历史服务情况.在每个时间窗tc,基站保存各用户的传输速率Tk(t)按照式(10)更新:
| $ {T_k}\left( {t + 1} \right) = \left\{ \begin{array}{l} \left( {1 - \frac{1}{{{t_c}}}} \right){T_k}\left( t \right) + \frac{1}{{{t_c}}}{R_k}\left( t \right),\;\;\;\;k = {k^ * }\\ \left( {1 - \frac{1}{{{t_c}}}} \right){T_k}\left( t \right),\;\;\;\;k \ne {k^ * } \end{array} \right. $ | (10) |
基站选择服务用户的规则为
| $ {k^ * } = \mathop {\arg \min }\limits_{k \in K} {U_1}\left( k \right) $ | (11) |
效用函数U1与基站的能量损耗正相关,而与公平性负相关.选择对应效用函数U1最小值的用户,可在保证用户相对公平性的前提下,减少基站系统的能量损耗,且随着公平性的增加,能量损耗的变化减缓,基站系统能量损耗趋于均衡.综上,间接法可分为边缘用户选择服务基站与各基站选取服务用户2个阶段.
阶段1 (边缘用户选择服务基站)
步骤1 初始化.
步骤2 对于位于微基站边缘的用户,逐一计算相应能源代价c1和c2,其中c1和c2分别为宏基站和微基站提供服务时对应的能源代价.
| $ {c_{\min }} = \min \left( {{c_1},{c_2}} \right) $ | (12) |
步骤3 在满足最低信干噪比的情况下,选取能源代价较小的基站为边缘用户提供服务.
| $ B = \left\{ \begin{array}{l} 1,\;\;\;\;{c_1} = {c_{\min }}\\ 2\;或\;3,\;\;\;其他 \end{array} \right. $ | (13) |
阶段2 (各基站选取服务用户)
步骤1 按照式(4)和式(9)计算各小区服务不同用户对应的能量损耗P和公平性J.
步骤2 逐一计算效用函数U1(k).
步骤3 在该微基站服务的所有用户(包括阶段1分配到微基站服务的用户)中选取对应效用函数U1较小的M个用户为服务用户.
2.2 直接法多源供电的系统中,可再生能源的产能速率与传统能源电价会发生变化,能量损耗和能源代价间并非简单的线性关系.同时,优先选用可再生能源产能速率较大的基站可减少传统能源的经济开销,从而大幅减少基站系统能源代价.直接法利用能源代价和用户间的公平性作为自变量,构造了一个指数型效用函数U2.该效用函数相当于在效用函数U1的底数前增加了一个随传统能源电价即可再生能源产能速率变化的价格因子.效用函数U2为
| $ {U_2}\left( {t,k} \right) = {C_k}{\left( t \right)^{\frac{1}{{{J_k}\left( t \right)}}}} $ | (14) |
式(14)为定义的“拓扑势”函数,描述了用户选择过程中能源代价与公平性间的关系.其中Ck(t)表示t时隙选择用户k对应的基站能源代价.
那么,小区选择服务用户的规则为
| $ {k^ * } = \mathop {\arg \min }\limits_{k \in K} {U_2}\left( {t,k} \right) $ | (15) |
类似于效用函数U1,效用函数U2与基站的能源代价正相关,而与公平性负相关.选择对应效用函数U2最小值的用户,可在兼顾公平性的情况下,减少基站系统能源代价,并且随着公平性的增加,其变化越来越平缓,从而使得系统能源代价趋于均衡.其具体过程如下.
阶段1 (边缘用户选择服务基站)与间接法相同.
阶段2 (各基站选取服务用户)
步骤1 确定该时间窗所在时隙对应的传统能源q1t,价格按照式(7)和式(9)计算各小区服务不同用户对应的能源代价C和公平性J.
步骤2 逐一计算效用函数U2(k, t).
步骤3 在该微基站服务的所有用户(包括阶段一分配到微基站服务的用户)中选取对应效用函数U2较小的M个用户为服务用户.
3 仿真参数和仿真结果假设1个宏基站位于坐标位置(0, 0)处,在每个时间窗内随机分布30个用户.笔者重点分析了微基站数Np=2情况,并分析了能量损耗和能源代价随微基站数目的变化情况.此外,传统能源采用峰谷分时电价策略,并设置电价系数为α.时间窗tc可根据实际情况进行设定,不妨设时间窗tc=10 s.
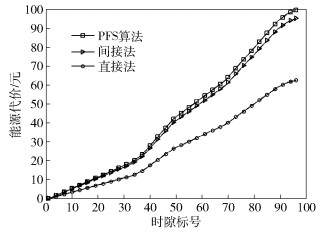
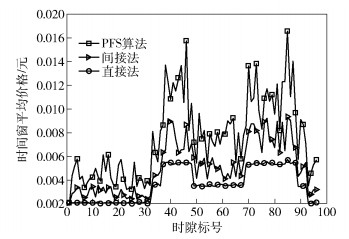
图 1~图 3分别对比了2个微基站的异构网络通信系统中不同算法的能源代价、时间窗平均价格和能量损耗.由图 1可知,3种算法的能源代价曲线变化趋势相同.所提出的直接法和间接法在保证公平性的前提下,偏向于选择同一小区中对应能量损耗较小的用户,使得能源代价显著下降.间接法可减少能源代价4.46%,而直接法又减少了34.44%的能源代价. 图 2说明了各算法的时间窗平均代价的对比情况. 3种算法的平均代价曲线与传统能源价格趋势相同.由于各个时间窗边缘用户分配情况与选择的服务用户不同,价格曲线伴随着不同程度的波动.而直接法和间接法可在不同程度上减少波动幅度,其中直接法的效果最为显著,可将波动幅度限制在4.57%以内. 图 3直观地显示了3种算法的能量损耗情况.基站系统的能量损耗与时间近似呈正比关系.其中,间接法能量损耗占PFS算法能量损耗的95.55%,而直接法的能量损耗仅62.72%.直接法不仅考虑了可再生能源产能速率,还兼顾了各时隙传统能源的价格,其自适应价格因子的存在使得该算法展现出突出的优势.
|
图 1 不同算法的能源代价对比 |
|
图 2 不同算法的时间窗平均代价对比 |

|
图 3 不同算法的能量损耗对比 |
为更清楚地说明基站系统能量损耗和能源代价随微基站数目的变化情况,还依次搭建了包含有4、6、8、10个微基站的异构网络通信系统模型,并进行了相关仿真分析,如图 4、图 5所示.由于间接法通过减少基站系统能量损耗的方式降低了系统能源代价,并没有考虑各时隙可再生能源产能速率的差异对于能源代价的影响,所以利用间接法与PFS算法的基站系统能量损耗变化趋势相同,且能量损耗的增长率逐渐降低.相比于PFS算法,间接法可减少能量损耗约3.20%,而直接法则综合考虑了系统能量损耗、可再生能源产能速率以及公平性,直接优化能源代价,因此其能量损耗与微基站数目呈正比例关系,并且在间接法的基础上可降低能量损耗52.75%,如图 4所示. 图 5描述了基站系统能源代价与微基站数目间的关系,3种算法的变化趋势与图 4中对应算法的能量损耗变化趋势一致.其中,相比于PFS算法,间接法可降低系统能源代价3.16%,直接法可降低能源代价67.89%.

|
图 4 不同算法的能量损耗对比 |

|
图 5 不同算法的能源代价 |
直接法、间接法与PFS算法中均考虑了用户间相对公平性的影响,表 1所示为微基站覆盖范围内各用户被服务次数占比情况.由表 1可知,与无公平性算法相比,PFS算法、间接法和直接法均考虑了边缘用户的公平性,使得边缘用户被服务次数的占比有了不同程度的提升.其中间接法中,中心用户被服务次数与边缘用户被服务次数之比为2.67:1,并可以使边缘用户平均被服务次数占比提升2.61%.直接法中,中心用户被服务次数与边缘用户被服务次数之比为3.32:1,同时可使边缘用户平均被服务次数占比提升1.79%.间接法可在降低系统能量损耗,间接减少能源代价的同时,显著提高用户间的相对公平性;而直接法可保证基站系统的能源代价最小,在一定程度上提升公平性,并且展现出与PFS算法相近的公平性性能.
|
|
表 1 微基站1中各用户被服务次数占比 |
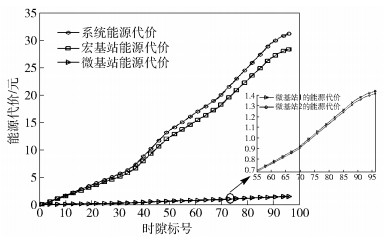
以直接法为例,图 6和图 7分别描述了各基站的能源代价及能量损耗情况.由图 6可知,宏基站的能源代价与系统能源代价具有相同的变化趋势,其曲线斜率主要由传统能源价格决定,受到可再生能源产能速率的影响.宏基站的能源代价占基站系统总能源代价的90%以上,而微基站的能源代价处于较低水平,约为宏基站能源代价的5%,由于2个微基站配置的新能源产能装置不同,使得微基站的能源代价略有差异.从图 7可知各基站能量损耗的情况.从宏观上而言,能量损耗与时间近似呈正比例函数.宏基站的能量损耗约为基站系统能量损耗的90.93%,而微基站的能量损耗约为宏基站能耗的5%.由于微基站分布在宏基站的对称位置,且微小区内及微小区边缘用户数相同,所以其能量损耗曲线基本重合.
|
图 6 不同算法的能源代价 |

|
图 7 各基站能量损耗情况 |
针对多源供电的无线异构网络,综合考虑了分时电价策略、可再生能源产能速率及用户公平性3种因素,研究了能量损耗与能源代价间的关系,提出了2个基于能源代价的用户选择算法.所提算法将用户选择分为2个阶段,兼顾了小区边缘用户的分配问题与小区内用户的用户选择问题.仿真结果表明,与传统PFS算法相比,间接法可以使用户间的相对公平性进一步提高,同时降低能量损耗,减少能源代价.而直接法中“自适应价格因子”的存在使得能量损耗与能源代价进一步下降30%以上.此外,以直接法为例研究了各基站的能量损耗及能源代价情况.宏基站的能量损耗占系统能量损耗的90%以上,由于宏基站能量损耗造成的能源代价是影响基站系统能源代价的主要因素,相比于宏基站而言,微基站的新能源供电量占据更大比例,因此配置可再生能源产能装置的差异对于微基站能源代价的影响更为显著.
| [1] | Lin Yan, Wang Yi, Li Chunguo, et al. Joint design of user association and power allocation with proportional fairness in massive MIMO HetNets[J]. IEEE Access, 2017, 5(99): 6560–6569. |
| [2] | Zhang Tiankui, Xu Hongzhang, Liu Dantong, et al. User association for energy-load tradeoffs in HetNets with renewable energy supply[J]. IEEE Communications Letters, 2015, 19(12): 2214–2217. doi: 10.1109/LCOMM.2015.2483508 |
| [3] | Elia. Power Generation[EB/OL]. [2016-11-23]. http://www.elia.be/en/grid-data. |
| [4] | Bu Shengrong, Yu F, Cai Yegui, et al. When the smart grid meets energy-efficient communications:green wireless cellular networks powered by the smart grid[J]. IEEE Transactions on Wireless Communications, 2012, 11(8): 3014–3024. |
| [5] | Abiri M, Mehrjoo M. Improving the performance of cell edge users with fractional coordinated fair scheduling[J]. Communications Letter, 2014, 8(13): 2315–2321. |


