2. 重庆大学 通信与测控中心, 重庆 400044
针对多小区协作多入多出(MIMO)系统中存在的信道状态信息(CSI)反馈回传过多的问题,提出了多小区部分协作MIMO系统预编码算法.首先建立了包含信道估计、量化和延时误差的联合误差模型,然后根据此信道误差模型,利用迫零和信漏噪比算法思想,提出一种多小区部分协作下的双层MIMO鲁棒预编码算法.数值分析及仿真结果表明,所提算法相比传统的多小区协作下行MIMO系统预编码算法,用户的误码率性能和系统和速率稍差,但在CSI反馈比特方面有一定优势.
2. Center of Communication and TT & C, Ministry of Education, Chongqing University, Chongqing 400044, China
In order to reduce the feedback bits of channel state information (CSI) in multi-cell cooperative multiple input multiple output (MIMO) system, a multi-cell partial cooperative MIMO precoding algorithm is proposed. Firstly, a joint channel error model including channel estimation error, quantization error and delay error, is established. Then, by using zero forcing and signal to leakage and interference ratio, a double-layer MIMO robust precoding algorithm is proposed. Numerical analysis and simulation results show that, compared with the traditional multi-cell MIMO system precoding algorithms, the bit error rate and the sum rate capacity are slightly worse, but the proposed algorithm has great advantage in CSI feedback bits.
郝东来等[1]使用信漏噪比(SLNR, signal to leakage and interference ratio)抑制小区内干扰.顾军等[2]利用块对角化(BD, block diagonalization)算法消除小区间干扰,并根据最小均方误差(MMSE, minimum mean-square error)准则来设计预编码向量以抑制小区内干扰.但是上述算法均假设信道状态信息(CSI, channel state information)理想,而且上述算法均基于传统的多小区协作模型,均要求基站(BS, base station)间共享大量CSI.
多小区协作下行多入多出(MIMO, multiple input multiple output)预编码技术可以有效消除小区间干扰,极大提升频谱效率,但是多小区协作下BS需要共享大量的CSI.基于频分双工的通信系统,信道估计在用户端进行,BS需要通过用户反馈方式获得CSI,这会占用大量的系统开销,而且在某些偏远的地区,BS间传输CSI采用无线传输方式,回传链路容量受限,大量的CSI反馈和回传对于通信系统而言是个极大的负担.因此,如何减少CSI,并消除干扰,是笔者关心的重点.
笔者考虑了多小区部分协作MIMO预编码问题.首先,针对CSI非理想造成的系统损失问题,考虑引入鲁棒性的预编码算法,并提出联合信道误差模型;然后,针对多小区协作下CSI反馈回传过多的问题,提出部分协作的双层预编码算法,其中外层预编码采用干扰清零算法,以消除边缘用户受到的小区间干扰,内层预编码采用鲁棒SLNR算法,用来抑制小区内干扰.
1 系统模型考虑多小区多用户下行MIMO系统,协作BS个数为C,BS间部分协作,BS配置M根发送天线,每个用户配置单根接收天线,如图 1所示.
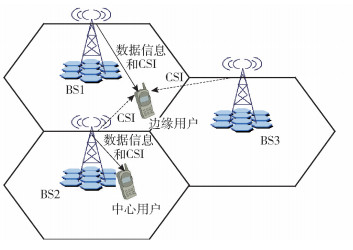
|
图 1 多小区部分协作MIMO系统示意图 |
用户(k, i)表示第i个BS中的第k个用户,由BSj到用户(k, i)的信道矩阵表示为gj(k, i)∈C1×M,信道经历时间和频率平稳衰落,其元素相互独立且为零均值、单位方差的复高斯随机变量.令v(k, i)(M×1矩阵)和x(k, i)分别为BSi是用户(k, i)设置的预编码向量和原始数据信号,则用户(k, i)接收到的信号表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_{\left( {k,i} \right)}} = \mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}{\mathit{\boldsymbol{v}}_{\left( {k,i} \right)}}{\mathit{\boldsymbol{x}}_{\left( {k,i} \right)}} + \sum\limits_{\begin{array}{*{20}{c}} {l = 1}\\ {l \ne k} \end{array}}^K {\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}{\mathit{\boldsymbol{v}}_{\left( {l,i} \right)}}{\mathit{\boldsymbol{x}}_{\left( {l,i} \right)}}} + }\\ {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^C {\sum\limits_{l = 1}^K {\mathit{\boldsymbol{g}}_j^{\left( {k,i} \right)}{\mathit{\boldsymbol{v}}_{\left( {l,j} \right)}}{x_{\left( {l,j} \right)}}} } + {n_{\left( {k,i} \right)}}} \end{array} $ | (1) |
其中:第1项为有用信号;第2项为多用户干扰;第3项为多小区干扰;第4项n(k, i)表示用户(k, i)所接收到的高斯加性白噪声,其为零均值、方差为ξ(k, i)的复高斯随机变量.
按照用户所受到的小区间干扰程度,来区分中心用户和边缘用户,具体方法为
| $ r_i^{\left( {k,i} \right)} - r_j^{\left( {k,i} \right)} \ge {\rm{th}},\forall j = 1,2, \cdots ,C\;且\;j \ne i $ | (2) |
其中:th≥0为预先设置的阈值,ri(k, i)为用户(k, i)受到小区内干扰信号的功率,rj(k, i)为用户(k, i)受到的协作BSj的干扰信号功率.若用户受到的干扰满足式(2),则为中心用户;否则为边缘用户.假定BSi中的激活用户个数用Ki表示,边缘用户个数用Di表示,系统中所有边缘用户个数为
假设hj(k, i)为用户k对原始信道矩阵gj(k, i)进行信道估计后得到的估计信道矩阵,则有以下信道估计模型[3]:
| $ \mathit{\boldsymbol{g}}_j^{\left( {k,i} \right)} = \mathit{\boldsymbol{h}}_j^{\left( {k,i} \right)} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_j^{\left( {k,i} \right)} $ | (3) |
其中:Δj(k, i)为1×M信道估计误差矩阵,其元素相互独立且均为零均x值、方差为σj(k, i)的复高斯随机变量.需要说明的是,Δj(k, i)与发送信号向量x、噪声向量n相互独立.
2.2 量化信道误差模型用户对信道进行估计以后,需要将hj(k, i)反馈给BS,假设采用随机矢量量化方法,从码本大小为2B的码本中根据最小距离原则选择码字,量化信道矩阵hj(k, i)与信道矩阵hj(k, i)的关系为[4]
| $ \mathit{\boldsymbol{h}}_j^{\left( {k,i} \right)} = \sqrt {1 - z_j^{\left( {k,i} \right)}} \mathit{\boldsymbol{\bar h}}_j^{\left( {k,i} \right)} + \sqrt {z_j^{\left( {k,i} \right)}} \mathit{\boldsymbol{s}}_j^{\left( {k,i} \right)} $ | (4) |
其中:
延时信道建模通常采用平稳遍历马尔可夫块衰落方法[5],其数学形式表示为
| $ \mathit{\boldsymbol{h}}_j^{\left( {k,i} \right)}\left[ n \right] = \rho _j^{\left( {k,i} \right)}\mathit{\boldsymbol{h}}_j^{\left( {k,i} \right)}\left[ {n - 1} \right] + \mathit{\boldsymbol{e}}_j^{\left( {k,i} \right)}\left[ n \right] $ | (5) |
其中:hj(k, i)[n]和hj(k, i)[n-1]分别为时刻n和时刻n-1的信道矩阵;ej(k, i)[n]为延时误差矩阵,其元素为零均值、方差为1-(ρj(k, i))2的复高斯随机变量,且相互独立;参数ρj(k, i)=J0(2πfj(k, i)Ts), J0(·)为0阶第一类贝塞尔函数,fj(k, i)为多普勒频移,Ts为符号间隔.
2.4 联合信道误差模型在信道估计、量化和延时误差同时存在的情况下,根据式(3)~式(5),第n个时刻BSj到用户(k, i)的信道矩阵gj(k, i)[n]建模为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{g}}_j^{\left( {k,i} \right)}\left[ n \right] = \rho _j^{\left( {k,i} \right)}\left( {\sqrt {1 - z_j^{\left( {k,i} \right)}\left[ {n - 1} \right]} \mathit{\boldsymbol{\bar h}}_j^{\left( {k,i} \right)}\left[ {n - 1} \right] + } \right.}\\ {\left. {\sqrt {z_j^{\left( {k,i} \right)}\left[ {n - 1} \right]} \mathit{\boldsymbol{s}}_j^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right) + }\\ {\mathit{\boldsymbol{e}}_j^{\left( {k,i} \right)}\left[ n \right] + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_j^{\left( {k,i} \right)}\left[ n \right]} \end{array} $ | (6) |
考虑非理想CSI,提出具有鲁棒性的多小区部分协作MIMO双层预编码算法.内层预编码需要BS间部分协作,以消除边缘用户受到的小区间干扰;而外层预编码实际上是多用户MIMO预编码,以抑制小区内干扰,其不需要BS协作.
3.1 内层预编码内层预编码目的是为了完全消除边缘用户的小区间干扰.迫零(ZF, zero forcing)预编码是一种用户单天线下MIMO系统中消除干扰的典型算法.笔者利用多小区ZF预编码思想,对其做出部分改进,作为内层预编码算法.
用户(k, i)的内层预编码向量用u(k, i)表示,其选取原则为:用户(k, i)对协作区域中所有边缘用户的干扰为零,写成数学形式表示为
| $ \mathit{\boldsymbol{\bar h}}_i^{\left( {l,j} \right)}\left[ {n - 1} \right]{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}} = 0,\forall k,i,j \ne i,l \in \left[ {1,{D_j}} \right] $ | (7) |
把式(7)写成矩阵形式:
| $ {\mathit{\boldsymbol{H}}_{\left( {k,i} \right)}}{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}} = 0,\forall k,i $ | (8) |
其中H(k, i)为用户(k, i)的干扰矩阵,表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_{\left( {k,i} \right)}} = }\\ {\left[ \begin{array}{l} \mathit{\boldsymbol{\bar h}}_i^{\left( {1,1} \right)}\left[ {n - 1} \right], \cdots ,\mathit{\boldsymbol{\bar h}}_i^{\left( {{D_1},1} \right)}\left[ {n - 1} \right], \cdots ,\mathit{\boldsymbol{\bar h}}_i^{\left( {1,i - 1} \right)}\left[ {n - 1} \right], \cdots ,\mathit{\boldsymbol{\bar h}}_i^{\left( {{D_{i - 1}},i - 1} \right)}\left[ {n - 1} \right],\\ \mathit{\boldsymbol{\bar h}}_i^{\left( {1,i + 1} \right)}\left[ {n - 1} \right], \cdots ,\mathit{\boldsymbol{\bar h}}_i^{\left( {{D_{i + 1}},i + 1} \right)}\left[ {n - 1} \right], \cdots ,\mathit{\boldsymbol{\bar h}}_i^{\left( {1,C} \right)}\left[ {n - 1} \right], \cdots ,\mathit{\boldsymbol{\bar h}}_i^{\left( {{D_C},C} \right)}\left[ {n - 1} \right] \end{array} \right]} \end{array} $ | (9) |
根据干扰清零思想,从H(k, i)的右零空间中选择一组标准正交基作为用户(k, i)的预编码向量u(k, i),这样就可满足式(7).另外,为了使得用户(k, i)接收到的有用信号功率较大,选定u(k, i)在信道矩阵h i(k, i)的投影方向上,则用户(k, i)的内层预编码向量u(k, i)为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}} = }\\ {\left[ {\mathit{\boldsymbol{I}} - {{\left( {{\mathit{\boldsymbol{H}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{{\left( {{{\left( {{\mathit{\boldsymbol{H}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{H}}_{\left( {k,i} \right)}}} \right)}^{ - 1}}{\mathit{\boldsymbol{H}}_{\left( {k,i} \right)}}} \right]\mathit{\boldsymbol{\bar h}}_i^{\left( {k,i} \right)}\left[ {n - 1} \right]} \end{array} $ | (10) |
内层预编码使得边缘用户受到的多小区干扰被完全消除,但是用户受到的多用户干扰仍然存在,此时须利用外层预编码算法来消除多用户干扰.基于SLNR的预编码算法,其在最大化信号发射功率的同时,考虑最小化信号泄露功率与噪声之和,克服了ZF算法在信噪比(SNR, signal noise ratio)较低环境下性能下降的问题,且可运用于分布式MIMO通信系统中,因此选择SLNR鲁棒预编码算法作为外层预编码算法.
根据SLNR定义,假设用户(k, i)的外层预编向量用w(k, i)表示,则第n个时刻用户(k, i)的SLNR用S(k, i)[n]表示,定义如下:
| $ \begin{array}{*{20}{c}} {{S_{\left( {k,i} \right)}}\left[ n \right] = }\\ {\frac{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{{\left( {{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{{\left( {\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}}}{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}\sum\limits_{l = 1,i \ne k}^K {{{\left( {{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} \right)}^{\rm{H}}}{{\left( {\mathit{\boldsymbol{g}}_i^{\left( {l,i} \right)}\left[ n \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{g}}_i^{\left( {l,i} \right)}\left[ n \right]{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} + {\xi _{\left( {k,i} \right)}}}}} \end{array} $ | (11) |
外层预编码问题为求解功率约束下SLNR的最大化问题,即
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} {S_{\left( {k,i} \right)}}\left[ n \right]}\\ {{\rm{s}}.\;{\rm{t}}.\;\;{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}} \le {P_{\left( {k,i} \right)}}} \end{array} $ | (12) |
其中P(k, i)为用户(k, i)的最大发射功率.
优化问题(式(12))没有考虑非理想CSI对系统性能的影响.根据2.4节的联合信道误差模型,BS获得hj(k, i)[n-1],将优化问题式(12)中S(k, i)[n]更改为条件数学期望Ehi(k, i)[n]|hi(k, i)[n-1]{S(k, i)[n]},因此,基于SLNR下的鲁棒预编码问题为
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} {E_{\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]\;\left| {\mathit{\boldsymbol{\bar h}}_i^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right.}}\left\{ {{S_{\left( {k,i} \right)}}\left[ n \right]} \right\}}\\ {{\rm{s}}.\;{\rm{t}}.\;\;{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}} \le {P_{\left( {k,i} \right)}}} \end{array} $ | (13) |
化简Egi(k, i)[n]|hi(k, i)[n-1]{S(k, i)[n]}, 代入式(11),不难得出
| $ {E_{\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]\;\left| {\mathit{\boldsymbol{\bar h}}_i^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right.}}\left\{ {{S_{\left( {k,i} \right)}}\left[ n \right]} \right\} \ge \frac{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{{\left( {{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{E_{\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]\;\left| {\mathit{\boldsymbol{\bar h}}_i^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right.}}\left\{ {{{\left( {\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]} \right\}{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}}}{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}\sum\limits_{l = 1,i \ne k}^K {{{\left( {{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} \right)}^{\rm{H}}}{E_{\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]\;\left| {\mathit{\boldsymbol{\bar h}}_i^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right.}}\left\{ {{{\left( {\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]} \right\}{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} + {\xi _{\left( {k,i} \right)}}}} $ | (14) |
下面来化简式(14),根据联合信道误差模型(式(6))可得
| $ \begin{array}{*{20}{c}} {{E_{\mathit{\boldsymbol{h}}_i^{\left( {k,i} \right)}\left[ n \right]\;\left| {\mathit{\boldsymbol{\bar h}}_i^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right.}}\left\{ {{{\left( {\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{g}}_i^{\left( {k,i} \right)}\left[ n \right]} \right\} = }\\ {{{\left( {\rho _i^{\left( {k,i} \right)}} \right)}^2}\left( {1 - \delta _i^{\left( {k,i} \right)}} \right){{\left( {\mathit{\boldsymbol{\bar h}}_j^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{\bar h}}_j^{\left( {k,i} \right)}\left[ {n - 1} \right] + }\\ {{{\left( {\rho _i^{\left( {k,i} \right)}} \right)}^2}\delta _i^{\left( {k,i} \right)}{\mathit{\boldsymbol{I}}_M}} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {{E_{\mathit{\boldsymbol{h}}_i^{\left( {l,i} \right)}\left[ n \right]\;\left| {\mathit{\boldsymbol{\bar h}}_i^{\left( {l,i} \right)}\left[ {n - 1} \right]} \right.}}\left\{ {{{\left( {\mathit{\boldsymbol{g}}_i^{\left( {l,i} \right)}\left[ n \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{g}}_i^{\left( {l,i} \right)}\left[ n \right]} \right\} = }\\ {{{\left( {\rho _i^{\left( {l,i} \right)}} \right)}^2}\left( {1 - \delta _i^{\left( {l,i} \right)}} \right){{\left( {\mathit{\boldsymbol{\bar h}}_i^{\left( {l,i} \right)}\left[ {n - 1} \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{\bar h}}_i^{\left( {l,i} \right)}\left[ {n - 1} \right] + }\\ {{{\left( {\rho _i^{\left( {l,i} \right)}} \right)}^2}\delta _i^{\left( {l,i} \right)}{\mathit{\boldsymbol{I}}_M}} \end{array} $ | (16) |
为表述简洁,令
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}_i^{\left( {k,i} \right)} = {{\left( {\rho _i^{\left( {k,i} \right)}} \right)}^2}\left( {1 - \delta _i^{\left( {k,i} \right)}} \right){{\left( {\mathit{\boldsymbol{\bar h}}_j^{\left( {k,i} \right)}\left[ {n - 1} \right]} \right)}^{\rm{H}}} \times }\\ {\mathit{\boldsymbol{\bar h}}_j^{\left( {k,i} \right)}\left[ {n - 1} \right] + {{\left( {\rho _i^{\left( {k,i} \right)}} \right)}^2}\delta _i^{\left( {k,i} \right)}{\mathit{\boldsymbol{I}}_M}} \end{array} $ |
| $ \mathit{\boldsymbol{B}}_i^{\left( {k,i} \right)} = {E_{\mathit{\boldsymbol{h}}_i^{\left( {l,i} \right)}\left[ n \right]\;\left| {\mathit{\boldsymbol{\bar h}}_i^{\left( {l,i} \right)}\left[ {n - 1} \right]} \right.}}\left\{ {{{\left( {\mathit{\boldsymbol{h}}_i^{\left( {l,i} \right)}\left[ n \right]} \right)}^{\rm{H}}}\mathit{\boldsymbol{h}}_i^{\left( {l,i} \right)}\left[ n \right]} \right\} $ |
联立式(15)和式(16),则式(13)简化为
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{{\mathit{\boldsymbol{w}}_{k,i}}} \frac{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{{\left( {{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}\mathit{\boldsymbol{A}}_i^{\left( {k,i} \right)}{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}}}{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}\left[ {\sum\limits_{l = 1,i \ne k}^K {{{\left( {{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} \right)}^{\rm{H}}}\mathit{\boldsymbol{B}}_i^{\left( {l,i} \right)}{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} + \frac{{{\xi _{\left( {k,i} \right)}}}}{{{P_{\left( {k,i} \right)}}}}\mathit{\boldsymbol{I}}} \right]{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}}}}\\ {{\rm{s}}.\;{\rm{t}}.\;\;{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}} \le {P_{\left( {k,i} \right)}}} \end{array} $ | (17) |
式(17)是一个广义瑞利商问题,因此
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}} = }\\ {\arg \max \frac{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}{{\left( {{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}\mathit{\boldsymbol{A}}_i^{\left( {k,i} \right)}{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}}}{{{{\left( {{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}\left[ {\sum\limits_{l = 1,i \ne k}^K {{{\left( {{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} \right)}^{\rm{H}}}\mathit{\boldsymbol{B}}_i^{\left( {l,i} \right)}{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} + \frac{{{\xi _{\left( {k,i} \right)}}}}{{{P_{\left( {k,i} \right)}}}}\mathit{\boldsymbol{I}}} \right]{\mathit{\boldsymbol{w}}_{\left( {k,i} \right)}}}} = }\\ {{\mathit{\Phi }_{\max }}\left\{ {{{\left( {{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}}} \right)}^{\rm{H}}}\mathit{\boldsymbol{A}}_i^{\left( {k,i} \right)}{\mathit{\boldsymbol{u}}_{\left( {k,i} \right)}},\sum\limits_{l = 1,i \ne k}^K {{{\left( {{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} \right)}^{\rm{H}}}\mathit{\boldsymbol{B}}_i^{\left( {l,i} \right)}{\mathit{\boldsymbol{u}}_{\left( {l,i} \right)}}} + } \right.}\\ {\left. {\frac{{{\xi _{\left( {k,i} \right)}}}}{{{P_{\left( {k,i} \right)}}}}} \mathit{\boldsymbol{I}}\right\}} \end{array} $ | (18) |
其中Φmax{ ·}表示广义最大特征值对应的特征向量.
3.3 算法流程根据前文所述,所提的多小区部分协作下行MIMO鲁棒双层预编码算法的具体实现过程如下:
1) 用户测定其所受到的干扰程度,并根据式(2)判断其属于边缘用户还是中心用户;
2) BS统计边缘用户个数,并将边缘用户序号回传给所有协作BS;
3) BS对该小区服务用户和协作区域内所有边缘用户发送信道估计训练序列,用户端进行信道估计、量化并反馈给BS;
4) 根据式(10)得到用户(k, i)的内层预编码向量u(k, i);
5) 根据式(18)获得用户(k, i)的外层预编码向量w(k, i).
4 仿真结果下面通过仿真来比较和验证所提算法的性能.设定协作小区个数为3,BS间的距离为1 km,用户均匀分布在小区中. BS天线数为8,用户天线数为1,每个BS假设总用户个数为4,其中边缘用户2个.假设信道建模为独立同分布瑞利平坦衰落信道,信道矩阵元素相互独立且为零均值、单位方差复高斯随机变量.
图 2给出了系统和速率与SNR的关系.选择多小区下行鲁棒MMSE算法[6](C-MMSE)、多小区协作ZF算法[7](ZF)、多小区部分协作BD算法[8](P-ZF)和所提算法进行比较.设定延时fj(k, i)Ts=0.1(∀j, i, k),估计误差σ2=0.1,反馈比特B=12 bit.由图 2可以看出,C-MMSE算法的系统和速率性能最优,所提算法的系统和速率性能优于P-ZF和ZF算法,P-ZF算法最差.
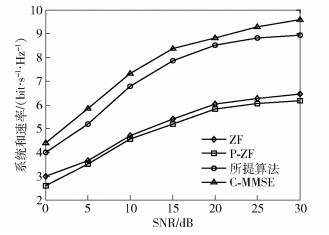
|
图 2 系统和速率与SNR的关系 |
图 3所示为误码率(BER, bit error rate)与估计误差σ2的关系.假设延时fj(k, i)Ts=0.05(∀j, i, k),反馈比特B=18 bit.由图 3可以看出,在存在估计误差时,所提算法边缘用户的BER优于P-ZF算法;随着估计误差增大,对估计误差无鲁棒性的P-ZF算法,残留干扰增多,BER性能恶化严重.
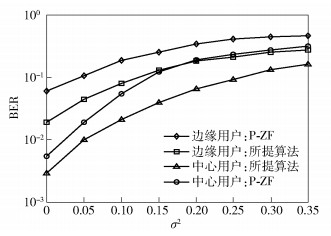
|
图 3 BER与估计误差的关系 |
仿真了BER与反馈比特B的关系,设置延时fj(k, i)Ts=0.05(∀j, i, k),估计误差σ2=0.05,结果如图 4所示.所提算法中心用户的BER性能最优,P-ZF算法边缘用户的BER性能最差,P-ZF算法中心用户的BER性能稍低于所提算法边缘用户的BER性能.

|
图 4 BER与反馈比特的关系 |
笔者研究了非理想CSI下的多小区下行MIMO鲁棒预编码问题.首先根据实际通信中存在的信道估计、量化和延时误差,建立了联合信道误差模型,并在此模型基础上提出了双层的多小区部分协作鲁棒预编码算法.仿真结果表明,所提算法相比传统的多小区协作下行MIMO系统预编码算法,用户的误码率性能和系统和速率稍差,但在CSI反馈比特方面优势明显.
| [1] |
郝东来, 隔建华. 一种多小区MIMO系统的分层预编码方案[J]. 西安电子科技大学学报, 2010, 37(4): 624–654.
Hao Donglai, Ge Jianhua. Layered-based precoding scheme for the multi-cell MIMO system[J]. Journal of Xidian University, 2010, 37(4): 624–654. |
| [2] |
顾军, 仲元红, 张振宇, 等. 用于多小区多用户MIMO系统的干扰抑制方法术[J]. 华南理工大学学报, 2013, 41(6): 42–46.
Gu Jun, Zhong Yuanhong, Zhang Zhenyu, et al. Interference suppression method for multi cell multiuser MIMO system[J]. Journal of South China University of Techno-logy, 2013, 41(6): 42–46. |
| [3] | Park H J, Lee K W, Lee Y H. Channel estimation using dedicated pilot for transmit beamforming in OFDM systems[C]//IEEE International Conference on Communications. Cape Town, South Africa: [s. n. ], 2010: 1-5. |
| [4] |
韩东升, 杨维. 多基站协作系统中有限反馈性能分析[J]. 北京邮电大学学报, 2013, 36(2): 79–83.
Hang Dongsheng, Yang Wei. Performance analysis of limited feedback in multi-base-station coordination systems[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 79–83. |
| [5] | Zhang Jun, Kountouris M, Andrews J G, et al. Multi-mode transmission for the MIMO broadcast channel with imperfect channel state information[J]. IEEE Transactions on Communications, 2011, 59(3): 803–814. doi: 10.1109/TCOMM.2011.121410.100144 |
| [6] | Dai Binbin, Xu Wei, Zhao Chunming. Optimal MMSE beamforming for multiuser downlink with delayed CSI feedback using codebooks[C]//IEEE Global Telecommunications Conference. Kathmandu, Nepal: IEEE, 2011: 1-5. |
| [7] | Zhang Hongyuan, Dai Huaiyu. Cochannel interference mitigation and cooperative processing in downlink multicell multiuser MIMO networks[J]. EURASIP Journal on Wireless Communications & Networking, 2004(2): 1–14. |
| [8] | Corvaja R, Fernandez J G, Armada A G. Partial coordination in clustered base station MIMO transmission[C]//Wireless Communications and Networking Conference. Shanghai: IEEE, 2013: 3146-3151. |


