2. 安徽理工大学 电信工程学院, 安徽 淮南 232001;
3. 安徽理工大学 能源与安全学院, 安徽 淮南 232001
针对目前井下传感器网络不能同时兼顾节点能量效率和能耗均衡性的问题,在混合通信方式基础上提出一种矿井无线传感器网络(WSN)自适应能量有效及能耗均衡的数据收集方法(AEBADA).首先通过比较分析确定了检测区域内环形宽度和节点最小通信半径,而在选择转发节点时不仅考虑节点距离和剩余能量,还包括链接的可靠性以及候选节点的邻居节点数目.仿真结果表明,相比同类混合通信方式和其他典型数据收集方法,AEBADA在节点效率和能耗均衡性以及路由可靠性方面优势明显,不受节点密度和分布状况影响,适用于井下通信环境.
2. School of Electrical Engineering and Information, Anhui University of Science and Technology, Anhui Huainan 232001, China;
3. School of Energy and Safety, Anhui University of Science and Technology, Anhui Huainan 232001, China
Node energy efficiency and energy consumption balance are two important aspects in wireless sensor networks (WSN), which have a direct impact on network life. In view of the fact that the underground sensor network cannot take account of both of them, an adaptive data collection method of node energy efficiency and energy consumption balance (AEBADA) was proposed on the basis of the hybrid communication mode. The ring width and the minimum communication radius of the node in the detection area are determined by comparative analysis. In selecting the relay node, not only the distance between nodes and the residual energy, but also the reliability of the link and the number of nodes adjacent to the candidate nodes are considered. Simulation shows that, compared with other similar hybrid communication scheme and some typical data collection methods, the AEBADA approach has obvious advantages in terms of node efficiency, energy consumption balance and routing reliability. It is not affected by the density and distribution of nodes and suitable for underground communication environment.
近年来无线传感器网络(WSN, wireless sensor network)被广泛用于煤矿井下.很多学者提出了很多能耗均衡的WSN路由方法和节点部署方式[1-5],但是多数并没有针对井下恶劣环境和通信要求而设计,难以在保证井下通信及时可靠的同时,兼顾WSN节点能量效率和能耗均衡.不少学者采用混合通信方式[6-8],节点的消息既可以通过逐跳转发至sink节点,也可以直接发送,但是还存在应用场合有限、链路可靠性差等局限.
目前还未有将这种WSN混合通信方式应用于井下环境的研究,笔者结合井下环境的特点,提出了一种矿井WSN自适应、能耗均衡的分布式数据收集方法(AEBADA, adaptive energy balanced approach for data gathering)算法,可以应用在节点均匀分布或随机分布的环境下,能提高节点能效的同时均衡网络能耗.
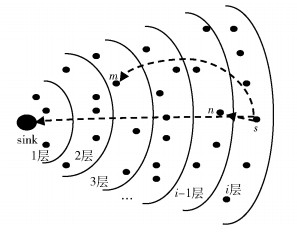
1 问题与建模 1.1 网络模型设N个传感器节点随机分布在监测区域内,sink节点位于中心,整个区域由n个半径分别为r,2r,3r,…,nr同心圆划分为多个环形,如图 1所示,第1层为sink节点所在的圆,向外依次为第2,3,…,N层环形.外层节点或通过内层的转发节点以多跳方式传递数据至sink,或直接发送给sink,或发给离sink更近的某个层.如图 1中节点s有多种选择发送消息.
|
图 1 混合通信示意图 |
假设网络满足以下条件:
1) 节点随机分布,每个节点在其邻近内层环内至少有一个转发节点.
2) MAC层采用RTS/CTS协议处理消息竞争冲突,即发送节点先广播RTS请求,收到请求的节点通过竞争以CTS响应,发送节点收到响应后开始传递数据.
3) 节点可以采用RSSI技术确定发送节点的距离,并且可以通过定位方法确定自己所在的位置,如位于第i个环形内.
4) 所有节点最小通信半径相同,且节点可以根据需要调整通信半径大小.
5) 通信链路对称.
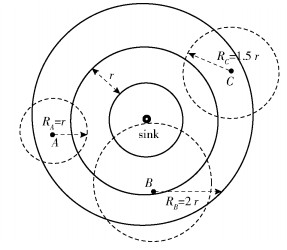
1.2 环形区域宽度的确定为保证相邻环形区域的节点能够相互通信,环形的宽度r应小于节点的通信半径R.如图 2所示,假设节点A、B、C的通信半径和环形宽度r的关系分别为RA= r、RB= 2r、RC=1.5 r,A靠近第i层边界外部,覆盖的第i-1层区域较小,所以A在i-1层的转发节点也少,所以宽度r取R不适合.同样,节点B位于第i层内侧,能覆盖到第i-2层环形区域的节点,会影响第i-2层节点通信.节点C的取值RC=1.5r是一个很好的折中.当C在第i层靠近外边界时,可以覆盖到第i-1层的中部位置,而当C位于第i层内边界区域时,能覆盖整个第i-1层区域.所以将区域内环形的宽度设定为
|
图 2 节点通信半径和环形宽度的关系 |
RTS消息包括{类型, 节点ID, 环形编号, 剩余能量, FLAG}等字段,CTS消息包括{类型, 节点ID, RTS节点ID, 环形编号}等字段.节点ID是节点唯一标识,FLAG置1时表示发送节点强制让邻近区域的节点竞争成为转发节点,即其剩余能量没有达到要求.
2.2 AEBADA算法过程系统启动后,由sink节点将网络参数以广播方式发给所有节点,包括节点最小通信半径Rmin、环的宽度r以及sink节点位置等信息,每个节点通过定位算法确定自己位置和所在的环形区域编号.
当位于第N层的节点i需要发送数据时,以半径Rmin广播RTS请求,RTS中包含了发送节点的剩余能量和所在环形区域编号(N)及目的区域编号(初始设为N-1)等信息.第N-1层内剩余能量不低于节点i的节点收到RTS后,启动定计器T,T的长短由多种因素决定,最终距离节点i远、剩余能量多、通信链路可靠性高、在外层邻居节点少的节点优先回复CTS消息,并当选为转发节点,比如节点j.其他竞争节点收到节点j的CTS消息后放弃竞争,节点i将数据转发给节点j.如果N-1环内没有符合要求的节点,节点i根据自身剩余能量大小,如果能量足够则直接发给sink节点,否则依次尝试发给N-2,N-3,…3,2等层的节点,直到找到合适的节点.如果以上所有尝试都没有找到转发节点,节点i把RTS字段中flag位置为1,以最初的半径Rmin广播出去,要求N-1层剩余能量最大的节点被选为转发节点.
节点在多跳通信时最小半径Rmin采用文献[9]中的Ropt,
| $ {{R}_{\text{min }}}={{R}_{\text{opt}}}=\sqrt[\alpha]{\frac{2{{\varepsilon }_{\text{elec}}}}{{{\varepsilon }_{\text{amp}*(\alpha -1)}}}} $ | (1) |
根据前面的论述,转发节点的选择考虑剩余能量、距离、链接可靠性以及邻居节点数,将定时器时间T表达式定义为
| $ T=\frac{\eta }{d{{E}_{\text{res}}}l} $ | (2) |
其中:η为节点收到其外层环内节点RTS的请求数,即为外层环的邻居节点数,η越大表示节点潜在能耗越大,越不适合被选为转发节点;d为接收到发送节点的距离;Eres为节点剩余能量;l表示接收和发送节点之间链路的可靠性,l值越低意味着冲突和重传的可能性越大.开始时l值设为1,以后节点每次回复CTS和接收数据后,用公式更新l值:
假设s首先向发送节点回复CTSs,其他竞争节点收到s的CTSs后清除自身定时器,放弃竞争.即使有些节点(节点t)没有收到节点s的CTSs,随后会收到发送节点发给s的数据(其中目的节点ID设为节点s),节点t知道节点s已经先于自己发送CTSs,从而放弃竞争.
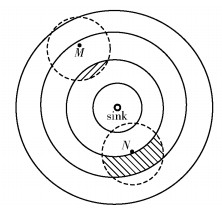
η的变化服从泊松分布,设节点分布密度为λ,图 3中下部的阴影部分的节点数即为节点N的η大小,当节点N靠近外层边缘时,覆盖的外层环形面积最大,进而η值最大.
|
图 3 节点覆盖的邻居层节点数 |
假设节点N覆盖的圆为CN,面积为SN,环区域i,i+1所在的圆形分别为Ci、Ci+1,对应面积分别为Si,Si+1,图 3中下面阴影部分面积为S,CN与Ci、Ci+1重叠部分的面积分别记为S1、S2,由图 3得
| $ S={{S}_{N}}-({{S}_{N}}-{{S}_{2}})-{{S}_{1}} $ | (3) |
节点N在第i+1层的邻居数
| $ \eta =S\lambda =({{S}_{N}}-({{S}_{N}}-{{S}_{2}})-{{S}_{1}})\lambda $ | (4) |
式(2)中相关参数分别取最大值或最小值时,定时器达到最大时间Tmax,其中的参数最大(小)值采用以下方式计算:
1) d最小值:当发送和接收节点距离很近时,取发射功率作为接收功率,进而用RSSI方法计算出d最小值.
2) η最大值:由式(4)计算η最大值.
3) Eres最小值:取节点以最小半径Rmin发送信号所必需的能量.采用Heinzelman等[10]提出的通信模型:
| $\left. \begin{align} &{{e}_{t}}\left( R \right)={{\varepsilon }_{\text{elec}}}b+{{\varepsilon }_{\text{amp}}}b{{R}^{\alpha }} \\ &{{e}_{r}}\left( R \right)={{\varepsilon }_{\text{elec}}}b \\ \end{align} \right\} $ | (5) |
其中:b为数据比特数,R为通信半径,α为衰减指数,εelecεamp分别为电路和放大器损耗.确定了R和b,et(R)即为所需Eres最小值.
4) l最小值取0.1,或者根据网络情况设置.
3 节点密度需求分析图 3中当节点M位于第i层靠近外边界时,M覆盖的第i+1层区域最小(图 3中上部的阴影部分).设这部分区域面积为A,节点服从泊松分布,则区域A内至少有一个节点的概率为
| $ p=1-{{\text{e}}^{-\lambda A}} $ |
定义1 设2个圆的半径分别为R1和R2,圆心之间距离为d(0<d<R1+R2),则2个圆重叠部分的面积A可以用式(6)计算:
| $ \begin{align} &A=R_{1}^{2}\text{co}{{\text{s}}^{-1}}\left( \frac{{{d}^{2}}+R_{1}^{2}-R_{2}^{2}}{2d{{R}_{1}}} \right)~+R_{2}^{2}\text{co}{{\text{s}}^{-1}}\left( \frac{{{d}^{2}}+R_{2}^{2}-R_{1}^{2}}{2d{{R}_{2}}}~ \right)- \\ &~\frac{1}{2}\sqrt{({{R}_{1}}+{{R}_{2}}-d)({{R}_{1}}-{{R}_{2}}+d)({{R}_{2}}-{{R}_{1}}+d)({{R}_{1}}+{{R}_{2}}+d)} \\ \end{align} $ | (6) |
图 3中区域A的面积为节点M覆盖的圆和圆Ci的重叠面积,可以由定义1计算而得,此时,R1=R, R2= (i-1)
| $ \begin{align} &A={{R}^{2}}\text{arccos}\left( \frac{8i+5}{12i} \right)+\frac{4}{9}{{\left( \left( i-1 \right)R \right)}^{2}}\times \\ &\text{arccos}\left( \frac{8{{i}^{2}}-8i-5}{8i\left( i-1 \right)} \right)-\frac{{{R}^{2}}}{18}~\sqrt{5\left( 4i+1 \right)\left( 4i-5 \right)} \\ \end{align} $ | (7) |
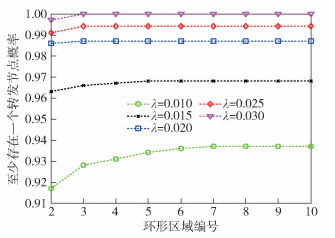
显然,当节点M位于第2层,即i=2时,区域A面积最小,代入式(7)得Amin=0.22R2. 图 4所示为节点通信半径R=30 m,节点密度在[0.01,0.03] (nodes/m2)变化时,区域A内至少存在一个节点概率的变化情况.由图可见,节点在其覆盖范围找到转发节点的概率全部高于0.9,多数情况下概率接近1.说明AEBADA算法可靠性较高,对节点密度要求低.
|
图 4 节点密度与存在转发节点概率的关系 |
为检验本文算法有效性和性能,使用Matlab将AEBADA算法分别与Zhu等[1]提出的PSO-EBR算法、典型的混合通信方式(EI[8])以及传统的多跳传递方式(简写为M)、单跳通信(简写为D)等4种算法在相同网络条件进行仿真,比较5种算法在能量效率、能耗均衡性和网络生存期以及路由可靠性方面的性能. PSO-EBR算法中的参数取值参照[1],其路由探测包生存期限取20.监测区域尺寸按煤矿采空区大小设定,α取4,节点初始能量为50 mJ, 最小通信半径35 m, 传感器节点密度为[0.01、0.05、0.1] nodes/m2, 其他参数参照文献[10],不考虑MAC层的能耗.
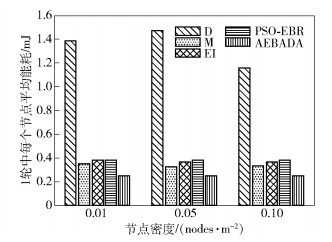
设sink节点收集完所有节点的信息所需要的时间为1轮. 图 5给出了5种算法在1轮中每个节点的平均能耗比较,其中M方式平均每轮0.335 mJ,但由于热区效应导致其能耗并不均衡. EI方式在一轮中节点平均能耗0.371 mJ,PSO-EBR的节点平均能耗为0.378 mJ,而AEBADA算法能耗为0.252 mJ,比PSO-EBR减少了33%,比EI减少了32%,按节点50 mJ的初始能量计算,则EI、PSO-EBR和AEBADA的生存期分别为135轮、132轮和198轮,AEBADA的生存期分别比PSO-EBR和EI增加了60轮和63轮.
|
图 5 不同密度下算法节点平均能耗比较 |
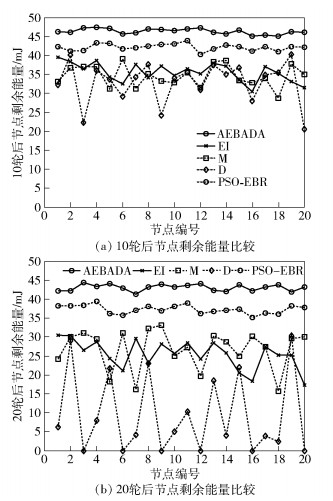
将监测区域中平均划分为20子区域,在每个区域随机挑选1个节点,图 6所示为5种算法分别在10、20轮以后20个节点的剩余能量情况(数据取10次仿真的平均值).由图可见,D、M、EI几种算法中节点的能耗差异较大. D方法20轮后离sink较远的节点已经耗尽失效. M中距离sink近的节点由于热区问题消耗了更多的能量,能耗均衡性差. PSO-EBR算法的适应度函数考虑了节点剩余能量,选择的路由能耗均衡较好,但路由探测过程和迭代计算增加了能量开销,AEBADA算法中节点的能耗最少,而且节点能量分布均衡,10轮和20轮后20个节点的剩余能量分别都在45 mJ和42 mJ以上,主要原因是AEBADA选择转发节点时综合考虑了多种因素,提高节点能量效率同时均衡网络能耗,有利于延长WSN网络寿命.
|
图 6 10、20轮后节点剩余能量比较 |
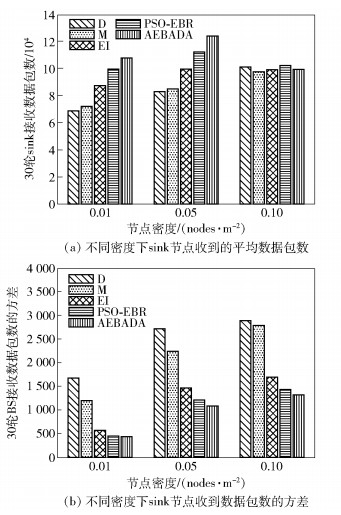
sink节点收到的数据包数目在一定程度上体现出路由的可靠性和稳定性,图 7所示为不同节点密度下5种算法在运行20轮中sink节点收到的数据包总数(取10次运行的平均值)及它们的方差.
|
图 7 不同节点密度下各算法sink节点收到数据包数的方差 |
由图 7可见,5种算法中sink接收数据包数都是随节点数的增加而增大.由于D、M、EI三种算法在30轮中先后出现失效节点,所以收到的数据包数目偏少,AEBADA算法平均接收的数据包数目最多,同时相应的方差最小,sink接收的数据包平均比其他4种算法分别增加了51%、46%、23%、8% (按图 7的次序).相比其他算法,AEBADA算法的路由可靠性和稳定性更好.
5 结束语在混合通信基础上提出一种适用在井下环境的AEBADA,能兼顾节点能量效率和能耗均衡性,不受节点的分布和密度影响,对节点的密度要求低.通过仿真比较,AEBADA平均节点能耗比同类的混合通信EI方法减少了32%,比PSO-EBR减少了33%. 10轮和20轮后20个节点的剩余能量分别都在45 mJ和42 mJ以上,30轮中Sink接收的数据包平均比其他4种算法分别增加了51%、46%、23%、8%,相比其他同类方法,AEBADA算法的网络寿命更长,路由可靠性和稳定性更好,更适合应用于井下工作环境.
| [1] |
朱永红, 丁恩杰, 胡延军. POS优化的能耗均衡WSNs路由算法[J]. 仪器仪表学报, 2015, 36(1): 78–86.
Zhu Yonghong, Ding Enjie, Hu Yanjun. Energy balance routing algorithm for WSNs optimized with PSO[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 78–86. |
| [2] |
任鹏, 张剑英, 冯小龙. 能耗均衡的煤矿井下巷道WSN跨层路由协议[J]. 煤炭学报, 2016, 41(2): 522–530.
Ren Peng, Zhang Jianying, Feng Xiaolong. Energy efficient cross-layer routing for wireless sensor network in coal mine roadway[J]. Journal of China Coal Society, 2016, 41(2): 522–530. |
| [3] |
张策, 张霞, 李欧, 等. 不可靠链路下急于压缩感知的WSN数据收集算法[J]. 通信学报, 2016, 37(9): 131–141.
Zhang Ce, Zhang Xia, Li Ou, et al. Compressive sensing based data gathering algorithm over unreliable links in WSN[J]. Journal on Communication, 2016, 37(9): 131–141. doi: 10.11959/j.issn.1000-436x.2016185 |
| [4] |
陈零, 奎晓燕, 张士庚, 等. 无线传感器网络分布式延迟受限低能耗数据收集算法[J]. 中南大学学报, 2015, 46(5): 1655–1662.
Chen Ling, Kui Xiaoyan, Zhang Shigeng, et al. Distributed delay-bounded energy-efficient algorithm for data gathering in wireless sensor networks[J]. Journal of Central South University (Science and Technology), 2015, 46(5): 1655–1662. doi: 10.11817/j.issn.1672-7207.2015.05.013 |
| [5] |
李成法, 陈贵海, 叶懋, 等. 一种基于非均匀分簇的无线传感器网络路由协议[J]. 计算机学报, 2007, 30(1): 27–36.
Li Chengfa, Chen Guihai, Ye Mao, et al. An uneven cluster-based routing protocol for wireless sensor networks[J]. Chinese Journal of Computers, 2007, 30(1): 27–36. |
| [6] | Jarry A, Leone P, Nikoletseas S, et al. Optimal data gathering paths and energy-balance mechanisms in wireless networks[J]. Ad Hoc Netw, 2011, 9(6): 1036–1048. doi: 10.1016/j.adhoc.2010.11.003 |
| [7] | Boukerche. A, Efstathiou. D, Nikoletseas. S, et al. Exploiting limited density information towards near-optimal energy balanced data propagation[J]. Comput Commun, 2012, 35(18): 2187–2200. doi: 10.1016/j.comcom.2012.07.022 |
| [8] | Jarry A, Leone P, Powell O, et al. An optimal data propagation algorithm for maximizing the lifespan of sensor networks[J]. Distributed Computing in Sensor Systems (DCOSS), 2006: 405–421. |
| [9] | Holland M, Wang T, Tavli B, et al. Optimizing physical-layer parameters for wireless sensor networks[J]. ACM Trans Sensor Netw (TOSN), 2011, 7(4): 1–20. |
| [10] | Heinzelman W R, Chandrakasan A, Balakrishnan H. Energy-effcient communication protocol for wireless microsensor networks[C]//The 33rd Hawaii International Conference on System Sciences (HICSS'00). 2000: 8020-8030. |


