2. 河南理工大学 物理与电子信息学院, 河南 焦作 454000
为提高无线传感器网络中的节点定位精度,提出一种自适应随机游走模型的节点定位算法.首先将随机游走应用于网络拓扑结构连通性中,构建节点间相对距离模型,并设计自适应算法,提高该模型有效性;然后通过将该模型嵌入经典定位算法distance vector-hop(DV-Hop)中实现系统节点定位工作.仿真和实验结果表明,该算法具有良好的鲁棒性和定位精度,误差比DV-Hop算法减少了20%~30%.
2. School of Physics and Electronic Information, Henan Polytechnic University, Henan Jiaozuo 454000, China
In order to improve node localization accuracy, a node localization algorithm based on adaptive random-walk module was presented for wireless sensor networks. First, a novel metric for relative distance among node sensors was modeled by applying the idea of random walk to the connectivity of system topology. Then an adaptive approach was designed to increase the validity of the metric. At last, node positions were finally obtained by embedding the metric in the classical localization algorithm distance vector-hop (DV-Hop). Simulation and outdoor environment's results show that the design achieves better robustness and positioning performance, and localization errors of the proposed method reduce by about 20%~30% compared with that of DV-Hop algorithm.
无线传感器网络(WSN, wireless sensor network)中,交互信息的有效性是建立在获取节点位置信息基础上的. WSN中节点定位技术主要着眼于定位时是否需要获得节点间的距离信息,分为基于测距的定位算法和无需测距的定位算法[1-2]两大类别.随机游走[3]指无规则行走者在时间间隔内以相同的概率移动到相邻位置,主要应用于研究朋友推荐技术[4]和链路预测[5]问题.此外,在生物信息学领域,Cao等[6]利用随机游走提出了图像扩散性质概念,对蛋白质相互作用网络中未知蛋白质进行功能预测. Chen等[7]将图像扩散性质用于WSN节点定位中,但仿真过程设定随机游走步数始终固定,不能保证不同网络环境配置的适用性.因此,笔者在此相关工作基础上,着重讨论随机游走步数和节点定位误差之间的关系,提出一种基于自适应随机游走距离(ARD, adaptive random-walk distance)的WSN定位算法,使得在不同网络环境配置下都可以自适应调整步数以保障提高定位精度.
1 算法设计本节介绍节点间相对距离模型和自适应游走步数的取值算法,给出优化相对距离模型完整流程,最终获取未知节点位置坐标.
1.1 相对距离模型根据文献[7],不失一般性,设已知全体节点数量为N的WSN部署在二维平面空间内,该网络拓扑结构表示为无向图G=(V, E),其中全体节点集合为V={v1, v2, …, vN},并且|V|=N,而E为边的集合. A无向图G的N阶邻接矩阵,其元素aij表示节点对(vi, vj)的连通关系.计算两点间随机游走距离(RD, random-walk distance)共有5个步骤.
1) 计算随机游走模型一步转移概率矩阵T〈1〉
T〈1〉中每一项tij〈1〉表示节点vi随机游走1步到达节点vj的概率,由式(1)求得.
| $ t_{ij}^{\left\langle 1 \right\rangle }=~\left\{ \begin{align} &\frac{1}{\sum\limits_{l=1}^{N}{{{a}_{il}}}}, \ \ {{a}_{ij}}=1 \\ &0, \text{ }{{a}_{ij}}=0 \\ \end{align} \right. $ | (1) |
2) 计算两点间多步转移概率
设随机游走步数为s(s≥2),则两点间多跳的转移概率记为tij〈s〉,表示节点vi随机游走s步到达节点vj的概率.由于每一步随机游走事件是相互独立的,一条路径的概率应表示为每跳转移概率的乘积,如果节点vi到节点vj存在多条s步路径,则多步转移概率为每条路径概率的加和.同时,所有节点对间s步转移概率可组成s步转移概率矩阵T〈s〉,有T〈s〉=(T〈1〉)s.
3) 计算两点间s步累加转移概率
随机游走过程中从第1步到第s步产生的两点间转移概率累加和即为s步累加转移概率,如式(2)所示.
| $ m_{ij}^{\left\langle s \right\rangle }=\sum\limits_{l=1}^{s}{t_{ij}^{\left\langle l \right\rangle }} $ | (2) |
4) 定义节点s步累加概率向量
对于任意节点vi,将其到所有节点的s步累加转移概率组成N维行向量即M〈s〉(vi),如式(3)所示.
| $ \mathit{\boldsymbol{M}}{{~}^{\langle s\rangle }}({{v}_{i}})=(m_{i1}^{\left\langle s \right\rangle }, m_{i2}^{\left\langle s \right\rangle }, \cdots, m_{iN}^{\left\langle s \right\rangle }) $ | (3) |
5) 计算两节点间RD
随机游走s步后两点间RD为
| $ D_{\text{RD}}^{\left\langle s \right\rangle }({{v}_{i}}, {{v}_{j}})=\|{{\mathit{\boldsymbol{M}}}^{\langle s\rangle }}({{v}_{i}})-{{\mathit{\boldsymbol{M}}}^{\langle s\rangle }}({{v}_{j}}){{\|}_{1}} $ | (4) |
其中‖…‖1为L1范式,即求向量差中各项绝对值之和.不难得出,当步数s为固定值时,DRD〈s〉(vi, vj)≡ DRD〈s〉(vj, vi),并有DRD〈s〉(vi, vi)≡0.
1.2 自适应s取值算法 1.2.1 提出问题相对距离模型中随机游走步数需人为给定,不同s取值会造成RD计算值差异,进而影响最终节点定位效果,这里讨论2种极端情况(s=1和s→+∞)下的计算影响.
1) s=1
随机游走1步后,计算得出的节点累加概率向量中仅仅在相连通的邻居节点位置上有数据,其余皆为0值.这在大规模不均匀网络中,不仅可能会导致各节点的累加概率向量中出现大量无意义的0值,也会造成多数节点对RD计算值相同的情况.如果一个相同的RD对应不同的实际物理距离,会导致节点定位歧义性问题.
2) s→+∞
随机游走是马尔可夫链的一个应用,每一次转移过程与上一次过程有关系,与初始状态无关.在较长时间后,马尔可夫过程会存在一个稳定状态概率.也就是说,在s趋向于正无穷的过程中存在一个k(k<s),有T〈k〉=T〈k+1〉=…=T〈s〉(T〈k〉为中间状态转移概率矩阵).这些数值相等项在第3步骤被累加s-k+1次后会在最后一个步骤中全部消减去掉.由此可得出,当随机游走步数趋于无限大时,相对距离模型计算出的数值是恒定值.虽说最终结果稳定,但该取值方案根本无法实现.即使人为定义了一个较大的数值,但这不仅不能证明随机取值的最优化,也会大幅增加算法的复杂度.
上述2种极端取值方法并不可行,需要折中取值方案才能优化相对距离模型.
1.2.2 自适应s取值算法设计利用穷举法的思路,提出了一个基于已知锚节点的自适应s取值算法.综合考虑算法复杂度和上述分析,s的自适应取值循环范围划定为s∈{2, 3, …, NA},即从2开始到锚节点个数NA为止的正整数.设锚节点集合为X,算法过程如下:
第1步 将s置为初始值2.
第2步 利用所提出的模型计算各个锚节点对(vi, vj)的相对距离DRD〈s〉(vi, vj).
第3步 计算锚节点单位校正距离U即
| $ U=~\frac{\sum\limits_{i\ne j, {{v}_{i}}, {{v}_{j}}\in X}{{{d}_{ij}}}}{\sum\limits_{i\ne j, {{v}_{i}}, {{v}_{j}}\in X}{D_{\text{RD}}^{\left\langle s \right\rangle }\left( {{v}_{i}}, {{v}_{j}} \right)}} $ | (5) |
其中dij为锚节点对(vi, vj)间实际距离.
第4步 通过相对距离与单位校正距离相乘,计算各锚节点对(vi, vj)的估计真实距离
第5步 计算所有锚节点间估计距离与实际距离的偏差和,并存储步数和相应数值.
第6步 置s=s+1,并返回第2步.
循环结束后取出第5步中存储数据,使偏差和最小的对应步数作为自适应s的确定取值,记为s*.
1.3 ARD综合1.1节与1.2节内容,给出优化相对距离模型的算法流程.首先,对所有已知锚节点采用自适应s取值算法得到可以使相对距离模型效果最优化的准确取值s*.其中锚节点间的一步转移概率矩阵记为P1,多步累加转移概率矩阵记为Pa〈s〉,由式P1+P12+…+P1s计算而得,其每一行都表示各个锚节点的累加概率向量,时间复杂度为O(Na4).其次,对所有传感节点计算随机游走s*步下优化节点间相对距离,时间复杂度为O(N3).其中节点间一步转移概率矩阵记为T〈1〉,多步累加转移概率矩阵记为Ta〈s*〉.为区别于RD,将节点对(vp, vq)的优化相对距离命名为ARD,记DARD〈s*〉(vp, vq).整个算法的时间复杂度为O(NA4+N3).
伪代码如算法1所示.
算法1 ARD模型算法
输入:Adjacency matrix A
for s from 2 to NA with step 1 do
for each anchor pair (vi, vj) do
Compute the P1 of all anchors
Compute Pa〈s〉=P1+P12+…+P1s
Compute DRD〈s〉(vi, vj)
=‖Pa〈s〉(i, :)-Pa〈s〉(j, :)‖1
end for
Compute the U
for each anchor pair (vi, vj) do
Estimate the distance
end for
end for
s*=argmin(ε(s))
for each node pair (vp, vq) do
Compute the T〈1〉 of all sensor nodes
Compute Ta〈s*〉=T〈1〉+(T〈1〉)2+…+(T〈1〉)s*
Compute D〈s*〉ARD(vp, vq)
=‖Ta〈s*〉(p, :)-Ta〈s*〉(q, :)‖1
end for
输出:Matrix of ARD among all nodes
1.4 基于ARD定位算法相似于DV-Hop[8]算法,将优化相对距离替换跳数并提出DV-ARD定位算法.大体思路是将相对距离转化成绝对距离,并根据极大似然估计法求得位置坐标.不同于DV-Hop最短路径,优化模型可直接获得未知节点到每一个锚节点的相对距离.由此,DV-ARD仅需要将DV-Hop中锚节点的单位跳数校正距离替换为单位校正距离U,对此式(5)已做出详细说明,并使用单位校正距离与相对距离乘积估计未知节点与锚节点间实际距离,最终利用极大似然估计法定位未知节点坐标.
2 仿真评估从定位效果图例中评估该模型的定位效果,并从锚节点数量、节点密度和网络大小3个参数不同数值对定位误差的影响评估该模型的健壮性.
2.1 网络配置在仿真中,基于对数衰减通信模型[9]建立正方形的WSN,记为W(c, N, NA, R).其中,c为网络大小长度(宽度),单位为m;N为网络节点总数;NA为锚节点个数;R为通信半径.
特别声明的是,定义2种误差分析参数评估定位性能.一种是节点定位偏移Ld(vi),重点分析某节点vi(xi, yi)与其估计定位坐标(x′i, y′i)间的偏移程度,如式(6)所示;另一种是系统定位误差Le,重点分析整个网络所有节点的定位误差,如式(7)所示.
| $ {{L}_{\text{d}}}({{v}_{i}})=\sqrt{{{({{x}_{i}}-{{{{x}'}}_{i}})}^{2}}+{{({{y}_{i}}-{{{{y}'}}_{i}})}^{2}}}~ $ | (6) |
| $ {{L}_{\text{e}}}=\frac{\sum\limits_{i=1}^{N}{{{L}_{\text{d}}}\left( {{v}_{i}} \right)}}{\left( N-{{N}_{\text{A}}} \right)\times R} $ | (7) |
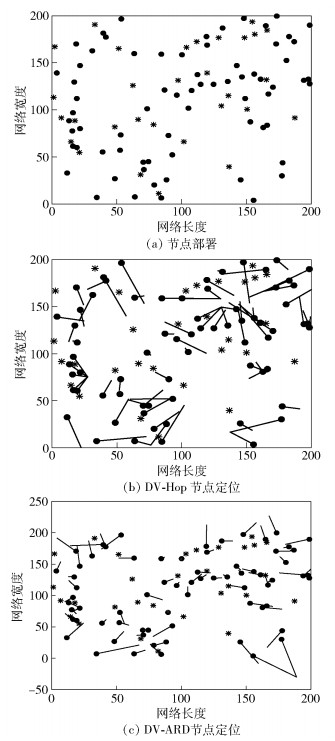
本节比较DV-Hop与DV-ARD定位效果. 图 1(a)描绘了非均匀的网络W(200, 100, 30, 50),星形为锚节点,圆点为待定位的未知节点.右上角和左下角的区域内节点密度较大,相应网络连通也更密集.仿真数据表明DV-ARD比DV-Hop的最大、最小以及平均Ld均小了1/4左右. 图 1(b)和(c)分别展示了2种算法的节点定位,线段圆点端为未知节点真实坐标,另一端表示该节点的估计位置,线段长短表示定位偏移.显而易见的是,图 1(c)中偏移线段数量与长度均略小于图 1(b)中线段,尤其是在节点密度较大的区域,DV-ARD定位优势更加明显.值得特别关注的是,图 1(b)中存在多条线段交于一点的现象,这正是跳数距离的离散映射带来了节点定位二异性问题,而这一问题在DV-ARD中得到了很好的解决.相应地,系统误差Le(DV-ARD)比Le(DV-Hop)减少了约14%.
|
图 1 DV-Hop与DV-ARD定位效果对比 |
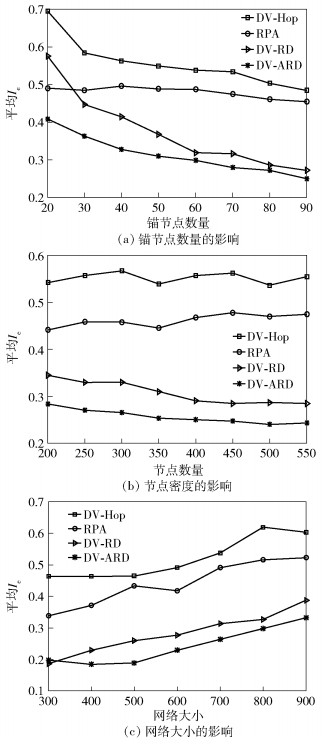
为验证DV-ARD定位健壮性,引入2种基于跳数距离的节点定位算法DV-Hop和鲁棒定位算法(RPA, robust positioning algorithm)[10]与所提算法进行误差分析比较,同时加入DV-RD算法表示s=20固定值下定位方法,比较分析自适应步数算法优势性. 图 2应用于网络W(700, 300, 70, 150)中,分别展示3种仿真参数对定位结果的影响.其中,横坐标分别代表不同参数取值,纵坐标代表 100轮仿真结果的平均Le.当一种参数取值变化时,该网络其余参数均不变.通过观察图 2可得,基于相对距离的定位算法的定位误差均小于基于跳数距离的定位算法,这表明前者在不同网络环境下具有定位表现的优异性.同时,随机游走步数的自适应比固定化方法更加适用于各种WSN.
|
图 2 仿真参数对定位结果的影响 |
1) 锚节点数量影响
图 2(a)表明随着锚节点数量的增加,各个算法都得到了定位效果的增进. DV-Hop和RPA这2种基于跳数距离的算法增速较缓,而基于相对距离(RD或ARD)的算法则效果改善速度较快.相较于其他3种算法,DV-ARD提高节点精度约24%、16%和7.5%.
2) 节点密度影响
在图 2(b)中,DV-Hop和RPA算法的定位误差变化较平缓但有所增长,说明节点密度的增大引发了跳数距离定位二异性的问题,但影响较小.反而基于相对距离定位的DV-RD和DV-ARD算法有微小的精度提高现象,这更加验证了相对距离模型的健壮性.相较于其他3种算法,DV-ARD提高节点精度约28%、20%和5.1%.
3) 网络大小影响
图 2(c)表明随着网络大小的扩张,由于通信半径保持不变,各种算法可利用的网络连通信息变少,其定位效果也相应变差.相较于其他3种算法,DV-ARD降低定位误差约22%、18%和4.1%.
3 实验 3.1 实验设计仿真部署了一个大规模非均匀的WSN,但无法真实模拟实际外界环境干扰,因此室外实验只证实DV-ARD良好的鲁棒性.实验在室外操场上采用25个CC2530节点部署了一个5×5的网格状WSN,横向或纵向节点间间距为5 m,如图 3所示.在实验中,每个传感器节点会广播80个发送功率为0 dBm的数据包,其中包含发送节点ID以及数据包的序列号信息.如果接收节点接收到的信号强度大于-100 dBm,就把发送节点的ID、相应的接收信号强度值、数据包序列号等信息写入到接收节点的闪存中;相反,此数据包就会被忽略掉.所有节点中闪存数据将通过自身通信模块上传至服务器中,利用Matlab软件即可处理获得所提算法所需的输入邻接矩阵.

|
图 3 实验场景 |
实验表明,与传统定位算法DV-Hop相比,DV-ARD节点定位算法具有良好的定位精度和鲁棒性特征. 表 1比较了2种算法定位节点的平均、最大和最小偏移量,计算后可得DV-ARD比DV-Hop的平均定位偏移值减少了约26%.
|
|
表 1 定位精度比较表 |
笔者主要介绍了一种基于自适应随机游走步数的节点定位算法.其主要思想是通过随机游走模型挖掘网络拓扑结构中连通性信息构建相对距离模型,并设计自适应步数的方法进一步优化该相对距离模型,最终通过嵌入经典算法替代跳数距离的方式实现节点的定位工作.经过大量的仿真和实验验证,DV-ARD算法在大规模网络尤其是密集区域具有良好的定位精度、健壮性和鲁棒性.相较于其他经典的节点定位算法,如DV-Hop算法,DV-ARD算法降低了20%~30%定位误差.
| [1] |
谭志, 张卉. 基于节点间覆盖关系的改进DV-Hop算法[J]. 北京邮电大学学报, 2014, 37(1): 35–38.
Tan Zhi, Zhang Hui. Improved DV-Hop localization algorithm based on coverage of nodes[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(1): 35–38. |
| [2] | Zhong Ziguo, He Tian. RSD:a metric for achieving range-free localization beyond connectivity[J]. IEEE Transactions on Parallel & Distributed Systems, 2011, 22(11): 1943–1951. |
| [3] | Fouss F, Pirotte A, Renders J M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. IEEE Transactions on Knowledge & Data Engineering, 2007, 19(3): 355–369. |
| [4] | Gong Jibing, Gao Xiaoxia, Cheng Hong, et al. Integrating a weighted-average method into the random walk framework to generate individual friend recommendations[J]. Science China Information Sciences, 2017, 60(11): 110–104. |
| [5] | Liu Weiping, Lu Linyuan. Link prediction based on local random walk[J]. A Letters Journal Exploring the Frontiers of Physics, 2010, 89(5): 58007–58012. |
| [6] | Cao M, Zhang H, Park J, et al. Going the distance for protein function prediction:a new distance metric for protein interaction networks[J]. PLoS One, 2013, 8(10): e76339. doi: 10.1371/journal.pone.0076339 |
| [7] | Chen Pengpeng, Yin Yuqing, Gao Shouwan, et al. Localization with graph diffusion property[J]. Sensors, 2017, 17(7): 1636. doi: 10.3390/s17071636 |
| [8] | Niculescu D, Nath B. DV based positioning in Ad hoc networks[J]. Telecommunication Systems, 2003, 22(1): 267–280. |
| [9] | Zhong Ziguo, He Tian. Achieving range-free localization beyond connectivity[C]//International Conference on Embedded Networked Sensor Systems. Berkeley: ACM, 2009: 281-294. |
| [10] | Savarese C, Rabaey J M, Langendoen K. Robust positioning algorithms for distributed ad-hoc wireless sensor networks[C]//General Track of the Conference on USENIX Technical Conference. USENIX Association, Monterey: ACM, 2002: 317-327. |


