2. 北京邮电大学 信息与通信工程学院, 北京 100876;
3. 奥本大学 材料工程系, 奥本 36849
以Sub-Miniature-A(SMA)型连接器为例,建立了基于等效电路法的同轴连接器S参数模型,给出了模型参数的计算方法,模拟了连接器的高频特性.特别是针对连接器接触表面退化,计算出了接触表面的高频电参数,建立了S参数与退化表面的关系,可作为连接器故障特征应用于连接器的寿命预测、可靠性评估以及故障诊断的研究.
2. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. Department of Materials Engineering, Auburn University, 36849, Auburn, AL, USA
S-parameters of Sub-Miniature-A (SMA) coaxial connector was calculated based on the equivalent circuit method, the high frequency characteristics of the connector effectively was simulated thereafter. Especially for the case of connector contact degradation, the parameters in the equivalent circuit model were calculated, and the relationship between the S-parameter and degraded level was established. The developed model could be used as a fault feature for the life prediction, reliability evaluation and fault diagnosis of the connector.
同轴连接器作为通信系统中不可或缺的基础部件, 用于实现设备间的电气连接或分离, 起到模块间信号传输的作用.受使用环境等影响, 连接器在工作过程中逐步退化, 尤其是接触面材料和形貌发生变化, 会导致连接器电参数退化, 影响通信信号的正常传输[1-2].因此, 建立连接器退化与电参数变化的关系, 从物理机理上研究连接器电参数的退化机理, 对于连接器的可靠性评估和制订连接器质量检测标准有着重要的参考价值.
Zhai等[3]对同轴高频继电器常闭型信号传输路径的阻抗参数进行提取, 建立了信号传输路径的等效电路模型. Ji等[4]研究了连接器接触表面不同退化程度对信号传输的影响, 并提取出接触阻抗参数. Yang等[5]对振动引起的连接器接触表面退化进行了实验与测试, 发现接触表面振动会产生电容效应.
S参数即散射参数, 是衡量器件及系统高频性能的重要指标.连接器S参数与其结构、材料、频率特性有关.笔者以Sub-Miniature-A(SMA)型同轴连接器为例, 建立连接器的等效电路模型, 分析接触表面退化引起的电路参数变化关系, 在连接器等效电路的基础上加入失效接触面引起的阻抗模型, 研究S参数的变化关系, 解释连接器接触退化对S参数的影响, 最后通过实验对模型进行验证.
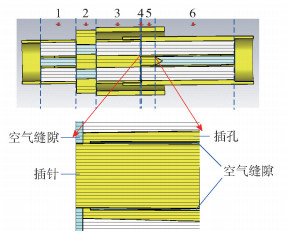
1 同轴连接器等效电路模型 1.1 研究对象SMA型连接器是通信系统中应用最为广泛的一种同轴连接器, 笔者以SMA型连接器为例进行研究.为了减小线缆等外部因素对测试的影响, 选用SMA型转接头作为研究对象.将一个SMA母转公转接头与母转母转接头进行连接, 组成一组研究样本, 该样本分为SMA母转公、SMA母转母以及接触区域3部分, 其结构剖面如图 1所示.按照SMA连接器样本的内外导体尺寸, 将样本划分为图 1中的6个区域进行研究, 其中区域4和区域5为插针与插孔的接触区域, 放大如图 1下半部分所示.
|
图 1 SMA连接器样本结构剖面图 |
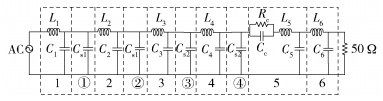
基于传输线理论, 将SMA连接器样本等效为多段均匀同轴线的级联, 高频电流的传播路径为内导体、介质层、外导体组成的闭合回路.对于每一段长度很小的均匀同轴传输线, 可以将其等效为电感与电容的并联电路.其中电感是由内外导体上的高频电流产生的, 电容是由内外导体及介质层的电压差产生的.对于接触区域, 如图 1中区域5所示, 由接触结构所致, 内导体插针插孔间的电接触仅发生在接触末端, 由于实际接触面积很小, 电流的收缩效应产生收缩电阻[6], 未接触区域(空气缝隙)形成电容.同时, 连接器样本存在内外导体尺寸变化的情况(区域1与区域2连接处、区域2与区域3连接处、区域3与区域4连接处、区域4与区域5连接处), 同轴内导体及外导体半径突变均可等效成一个附加在内外导体间的并联电容[7].因此SMA连接器样本等效电路建模如图 2所示.
|
图 2 SMA连接器样本等效电路 |
其中区域1、2、3为SMA母转公的等效电路, 区域6为SMA母转母的等效电路, 区域4、5为接触区域的等效电路. L1、C1、L2、C2、L3、C3、L4、C4、L5、C5、L6、C6分别为每段均匀同轴结构的等效电感和等效电容. Cs1、Cs2为连接器内外导体尺寸、介质变化区域(图 2中①②③④)所产生的寄生电容. Rc为接触区域的接触电阻, Cc为接触电容.
基于传输线理论, L1、C1、L2、C2、L3、C3、L4、C4、L5、C5、L6、C6可以通过式(1)和式(2)进行计算[7], 计算结果如表 1所示.其中微元数量依据每段区域的长度设置.
| ${{L}_{i}}=\frac{{{\mu }_{0}}{{\mu }_{i}}}{2\pi }\text{ln}\frac{{{b}_{i}}}{{{a}_{i}}} $ | (1) |
| $ {{C}_{i}}=\frac{2\pi {{\varepsilon }_{0}}{{\varepsilon }_{i}}}{\text{ln}\frac{{{b}_{i}}}{{{a}_{i}}}} $ | (2) |
|
|
表 1 等效电路参数提取结果 |
其中:ai为区域i的内导体外半径, i=1, 2, …, 6,bi为外导体内半径, μ0为真空磁导率, μi为导体的相对磁导率, ε0为真空介电常数, εi为介质层的相对介电常数.
关于尺寸及材料不连续区域所产生的寄生电容, 可通过曲线拟合的方式获得Cs1=0.055 pF和Cs2=0.001 pF.
由于连接器接触表面粗糙不平, 当2个粗糙面相接触时, 其接触面并非整个视在表面, 而是各表面凸起之间斑点的接触.由电接触理论可知, 通过接触斑点的电流线收缩, 使电阻增加, 这个增加的电阻定义为收缩电阻[6],计算公式为
| $ {{R}_{\text{c}}}={{R}_{\text{b}}}+\frac{\rho }{Nd} $ | (3) |
其中:Rb=1/2ρ×
根据接触表面微凸起的分布ϕ(z)可以求得实际接触面积Ar与视在接触面积Ab的关系以及实际接触点的个数[8].
| $ {{A}_{\text{r}}}={{A}_{\text{b}}}\int_{x}^{\infty }{\phi \left( z \right)\text{d}\mathit{z}} $ | (4) |
| $ {{N}_{\text{c}}}=\eta {{A}_{\text{b}}}\int_{x}^{\infty }{\phi \left( z \right)\text{d}\mathit{z}} $ | (5) |
假设ϕ(z)服从高斯分布, 式中η为单位面积上凸起的个数, x为接触表面的平均距离.经过计算可得SMA连接器的接触电阻Rc=1.65 mΩ.
除接触电阻外, 非接触区域同时产生接触电容[9].如图 2中区域5所示, 由接触产生的等效电路为接触电阻与接触电容的并联.接触电阻Rc= 1.65 mΩ, 假设接触电容Cc=0.73 pF, 则容抗为Zc= 1/jωC, 容抗的模值随着频率的升高而减小.当频率小于830 THz时, |Zc|>Rc, 当频率等于830 THz时, |Zc|=Rc, 当频率大于830 THz时, |Zc|<Rc.笔者考虑的频率范围远低于830 THz, 由于并联电路中阻抗取决于值小的支路, 所以未污染情况下接触电容的影响可以忽略, 接触阻抗|Zc|<1.65 mΩ.
当接触区域被污染膜覆盖时, 信号在接触区域的传播路径发生改变.如图 1所示, 假设污染膜均匀分布在插针插孔之间, 则电流通过电容耦合的方式在插针与插孔间传输.插针、污染膜、插孔构成了一个新的电容, 图 2中Rc、Cc随之改变为膜层电阻Rf以及膜层电容Cf, 该电容值可以按照同轴结构的电容计算方法进行计算.
| $ {{R}_{\text{f}}}=\frac{{{\rho }_{\text{f}}}{{s}_{\text{f}}}}{{{A}_{\text{b}}}} $ | (6) |
| $ {{C}_{\text{f}}}=\frac{2\pi {{\varepsilon }_{0}}{{\varepsilon }_{\text{f}}}{{l}_{\text{t}}}}{\text{ln}\ \frac{{{a}_{0}}+{{s}_{\text{f}}}}{{{a}_{0}}}}+\frac{2\pi {{\varepsilon }_{0}}({{l}_{\text{f}}}-{{l}_{\text{t}}})}{\text{ln}\ \frac{{{a}_{0}}+{{s}_{\text{a}}}}{{{a}_{0}}}} $ | (7) |
式中ρf为膜层电阻率, sf为膜层厚度, lt=0.1 mm为区域5末端电接触的长度, lf=1.49 mm为膜层覆盖长度, εf为膜层相对介电常数, a0=0.45 mm为插针半径.
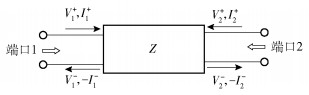
2 同轴连接器S参数模型将连接器样本的等效电路(见图 2)看作一个二端口网络, 如图 3所示.其中(V1+, I1+)为端口1入射波电压和电流, (V1-, -I1-)为端口1反射波电压和电流, (V2+, I2+)为端口二入射波电压和电流, (V2-, -I2-)为端口2反射波电压和电流.
|
图 3 等效二端口网络 |
S参数矩阵由入射和反射电压波之间的联系确定:
| $ \left[\begin{matrix} V_{1}^{-} \\ V_{2}^{-} \\ \end{matrix} \right]=\left[\begin{matrix} {{S}_{11}}&{{S}_{12}} \\ {{S}_{21}}&{{S}_{22}} \\ \end{matrix} \right]\left[\begin{matrix} V_{1}^{+} \\ V_{2}^{+} \\ \end{matrix} \right] $ | (8) |
S参数可确定为
| $ {{S}_{11}}=~{{\left. \frac{V_{1}^{-}}{V_{1}^{+}} \right|}_{V_{2}^{+}=0}}=\frac{Z_{\text{in}}^{\left( 1 \right)}-{{Z}_{0}}}{Z_{\text{in}}^{\left( 1 \right)}+{{Z}_{0}}}~ $ | (9) |
| $ {{S}_{22}}=~{{\left. \frac{V_{2}^{-}}{V_{2}^{+}} \right|}_{V_{1}^{+}=0}}=\frac{Z_{\text{in}}^{\left( 2 \right)}-{{Z}_{0}}}{Z_{\text{in}}^{\left( 2 \right)}+{{Z}_{0}}}~ $ | (10) |
| $ {{S}_{12}}=~{{\left. \frac{V_{1}^{-}}{V_{2}^{+}} \right|}_{V_{1}^{+}=0}} $ | (11) |
| $ {{S}_{21}}=~{{\left. \frac{V_{2}^{-}}{V_{1}^{+}} \right|}_{V_{2}^{+}=0}} $ | (12) |
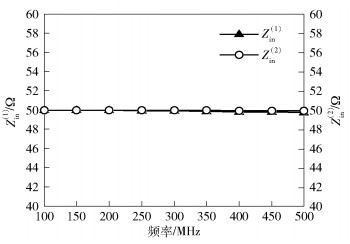
其中:Z0=50 Ω为匹配负载, 计算S11和S21时,Z0接在端口2, 计算S22和S12时,Z0接在端口1. Zin(1)为从端口1看向端口2的输入阻抗, Zin(2)为从端口2看向端口1的输入阻抗.将1.2节中计算所得的电路参数代入模型, 可以得到Zin(1)和Zin(2),如图 4所示.由计算结果可知, SMA型连接器样本从端口1看向端口2的输入阻抗Zin(1)与从端口2看向端口1的输入阻抗Zin(2)近似相等, 均为50 Ω.根据式(9)~式(12)可知, S11=S22, S21=S12, 即S参数具有对称性, SMA型连接器样本的可以看作为互易网络.
|
图 4 输入阻抗计算结果 |
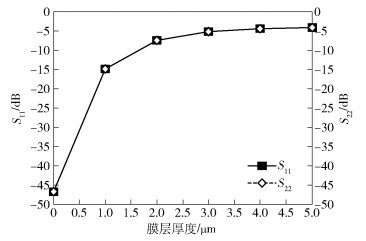
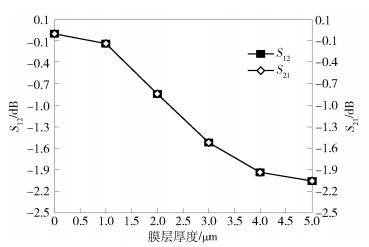
通过实验测试可知(见第3节), 接触表面污染膜主要成分为氧化镍, 因此εf=11.当信号传输频率为300 MHz时, 连接器S参数随膜层厚度的变化关系如图 5和图 6所示.结果显示, 存在氧化膜的连接器S11=S22, S21=S12, 说明接触表面退化并不会影响连接器的互易性.同时, S11随膜层厚度的增加而增大, S21随膜层厚度的增加而减小.
|
图 5 S11、S22与膜层厚度的关系 |
|
图 6 S12、S21与膜层厚度的关系 |
采用安捷伦矢量网络分析仪(N5071C)分别对崭新SMA连接器样本, 以及经历过加速试验后的SMA连接器样本进行S参数的测试, 测试仪器如图 7所示.测试频段为100~500 MHz.

|
图 7 S参数测试 |
为了得到加速试验后SMA连接器样本接触表面的材料变化, 采用扫描式电子显微镜(SEM,scanning electron microscope)以及能谱仪(EDS,energy dispersive spectrometer)对加速退化试验后连接器的接触材料及成分进行分析, 测试仪器如图 8所示.

|
图 8 SEM及EDS测试环境 |
为了模拟连接器接触表面退化对S参数的影响, 通过加速试验的方法得到表面存在污染膜的连接器样本.将一对SMA连接器样本拆开, 将公转母转接头的母头用聚四氟乙烯胶带隔离保护, 暴露出公头并放置于69%硝酸的蒸汽中3 h.为了便于检测腐蚀物成分, 将相同材料的内导体插针与上述样本同时放置于硝酸蒸气中3 h.加速腐蚀后可见公头内导体上出现铜锈.烘干处理后, 将母转公转接头与另一个母转母转接头连接, 从而产生退化连接器样本.将相同材料的内导体插针在打磨机上打磨, 得到带有腐蚀膜的插针截面, 用扫描电镜扫描并进行能谱分析, 观测腐蚀物成分, 实验结果显示, 腐蚀物主要成分为氧化镍, 氧化膜平均厚度为29.1 mm.
然后, 分别将崭新的SMA型连接器样本以及加速退化试验后的SMA型连接器样本, 用矢量网络分析仪进行S参数测试, 并分析加速退化前后S参数的变化, 研究污染的接触面对S参数的影响.
最后将实验测试结果与模型计算结果进行对比, 验证模型的准确性.
4 实验结果与讨论 4.1 S参数测试结果分析分别用矢量网络分析仪对未腐蚀的SMA连接器样本以及加速退化试验后的SMA连接器样本进行测试, S参数测试结果如图 9、图 10所示.
|
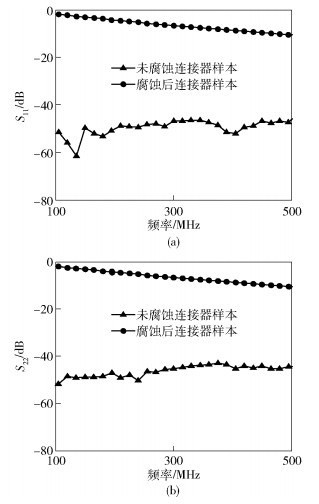
图 9 腐蚀前后SMA连接器样本的S11、S22参数 |
|
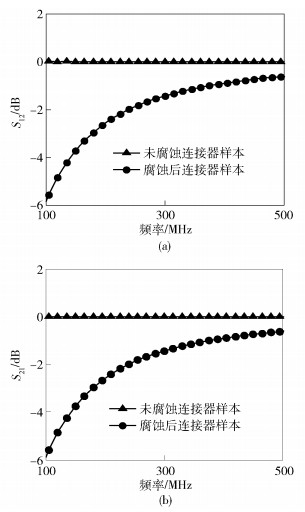
图 10 腐蚀前后SMA连接器样本的S21参数 |
结果显示, 无论腐蚀前后, 均有S11=S22, S12=S21, 说明SMA连接器等效为互易网络, 且接触界面退化并不会改变连接器的互易性.同时, 未腐蚀连接器的S11<40 dB, S12接近于0 dB, 说明在频率测试范围内, 未腐蚀的连接器回波损耗及插入损耗均很小, 信号在连接器内能够有效传输.而当连接器接触表面存在氧化膜后, S11、S22显著增加, S12、S21减小, 即接触部位氧化膜的存在会导致阻抗的不连续, 同时引起损耗增加.同时, 腐蚀后连接器的S11随频率的升高而减小, S12增大, 这是因为接触界面呈电容特性, 随着频率的升高, 阻碍减小且信号以电容耦合的方式从连接器母转公转接头传输到连接器母转母转接头.
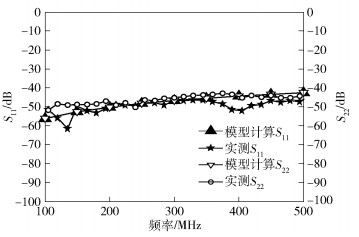
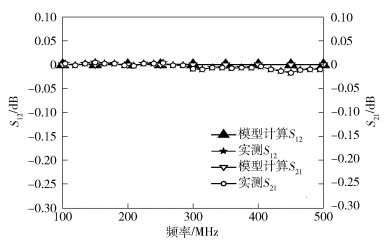
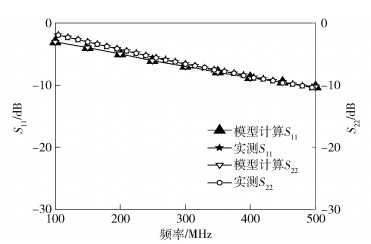
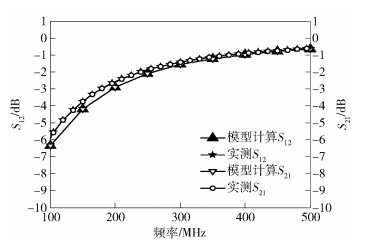
4.2 实测结果与模型计算结果对比对于一组典型的SMA型连接器样本, 当连接器接触表面退化后, 基于式(6)和式(7)计算可得接触表面等效电阻为Rf=360 Ω, 等效电容为Cf=10 pF.基于第2部分的理论分析, 按图 2所示等效电路模型分别计算接触表面退化前后连接器样本的参数.理论结果以及实测S参数结果如图 11~图 14所示, 结果显示建立的S参数模型能够有效的表征SMA型连接器的高频特性.实验结果验证了模型的有效性.
|
图 11 退化前实测S11、S22与模型计算结果对比 |
|
图 12 退化前实测S12、S21与模型计算结果对比 |
|
图 13 退化后实测S11、S22与模型计算结果对比 |
|
图 14 退化后实测S12、S21与模型计算结果对比 |
提出了一种基于等效电路法的同轴连接器S参数建模方法, 有效模拟了连接器的高频特性.同时分析了接触表面退化引起的电路参数变化关系, 建立了接触表面退化的连接器的S参数模型, 解释了连接器接触退化对S参数的影响机理.笔者所建立的模型, 能有效的从根本上解释环境污染对高频信号产生影响的机理, 为连接器的质量检测标准提供参考, 同时为连接器的可靠性评估与寿命预测提供理论依据.
| [1] | Shen Q, Lv K, Liu G, et al. Impact of electrical contact resistance on the high-speed transmission and on-line diagnosis of electrical connector intermittent faults[J]. IEEE Access, 2017(5): 4221–4232. |
| [2] | Ji R, Gao J, Xie G, et al. Fault analysis and diagnosis of coaxial connectors in RF circuits[J]. IEICE Transactions on Electronics, 2017, 100(11): 1052–1060. |
| [3] |
翟国富, 王新宇, 楚兵. 基于等效电路法的高频继电器建模与研究[J]. 中国电机工程学报, 2009(15): 119–124.
Zhai G, Wang X, Chu B. Modeling and study of high frequency relay based on equivalent circuit method[J]. CSEE, 2009(15): 119–124. doi: 10.3321/j.issn:0258-8013.2009.15.019 |
| [4] | Ji R, Gao J, Flowers G, et al. The effect of electrical connector degradation on high-frequency signal transmission[J]. IEEE Trans Compon Packag Technol, 2017, 7(7): 1163–1172. doi: 10.1109/TCPMT.2017.2688023 |
| [5] | Yang H, Tong Y, Flowers G, et al. Capacitance build-up in electrical connectors due to vibration induce fretting corrosion[C]//IEEE 62nd Holm Conference on Electrical Contacts. Clearwater: [s. n. ], 2016: 152-158. |
| [6] | Slade P G. Electrical contacts principles and applications[M]. New York: CRC Press, 2013: 5-11. |
| [7] | Whinnery J R, Jamieson H W, Robbins T E. Coaxial-line discontinuities[C]//Proceedings of Institute Radio Engineers. New York: [s. n. ], 1944: 695-709. |
| [8] | Greenwood J A, Williamson J B P. Contact of nominally flat surfaces[C]//Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. London: The Royal Society, 1966: 300-319. |
| [9] | Malucci R, Panella A. Contact physics of capacitive interconnects[J]. IEEE Trans on Compon Packag Tech-nol, 2013, 3(3): 377–383. doi: 10.1109/TCPMT.2012.2185798 |


