2. 清华大学 电机系, 北京 100084;
3. 国网河南省电力公司, 郑州 450052;
4. 中国电力科学研究院 用电与能效研究所, 北京 100192
为解决配电网拓扑不易监测的问题,提出了一种新型的智能配电网拓扑生成方法.首先利用最小绝对值收敛和选择算法(LASSO)得到配电网母线间的关联系数矩阵,然后通过逻辑"and"规则和基于电压关联分析模型的补充判据修正矩阵,最后基于修正后的电压关联系数矩阵生成配电网的拓扑结构.仿真实验结果表明,算法无需利用任何配电网的先验知识,仅基于时序电压数据即可高效准确地生成无环和有环的配电网拓扑.算法可作为监测实际运行配电网拓扑的辅助决策方法.
2. Department of Electrical Engineering, Tsinghua University, Beijing 100084, China;
3. State Grid Henan Electric Power Company, Zhengzhou 450052, China;
4. Power Consunption & Energy Efficiency Department, China Electric Power Research Institute, Beijing 100192, China
In order to solve the problem that the distribution network topology is difficult to monitor, a novel data driven algorithm is proposed to generate the distribution network topology. Firstly, the least absolute shrinkage and selection operator (LASSO) algorithm is adopted to obtain the correlation coefficient matrix of all buses in the network. Then, the "and" logic rule and the criteria based on the voltage correlation analysis model are utilized to correct the matrix. Finally, the topology is reconstructed based on the modified matrix. Simulation results show that the proposed algorithm can efficiently and accurately generate the un-loopy and loopy distribution network topology based on timing voltage data without using any prior knowledge of distribution network. The algorithm could be employed as an auxiliary decision-making method to generate the operational distribution network topology.
随着能源互联网的发展,配电网不仅是能量消耗终端,也是分布式能源的接入载体.分布式能源终端的大量接入为配电网带了机遇和挑战.融合人工智能的方法提高配电网的智能化水平是电网深化发展的重要需求[1-2].
电力系统的拓扑结构是其稳定和高效运行的重要基础.目前,针对电力系统拓扑的研究大多局限在对输电网拓扑错误的辨识,即刀闸开关遥信信号的偏差所导致的拓扑信息错误.方法主要有新息图法[3]、最小信息损失法[4]、支路电流状态估计法[5]、潮流计算法[6]等.由于配电网测量设备少,线路参数不完备,上述方法不能直接用于配电网.目前配电网的拓扑辨识主要依靠地理信息系统(GIS,geographical information system)的原始记录和人工现场巡查.
由于配电网重新配置频繁,地下线路设置复杂以及人为私自改动线路,导致GIS信息记录存在错误,而人工现场排查难度大,效率低.国内配电网一般采用“闭环设计,开环运行”的供电模式,即配电网初始布线是有环路的,运行时通过开关断开部分支路保证其无环运行.闭环设计是为了提高供电可靠性,开环运行是为了避免形成电磁环网,增大短路电流等故障.配电网有环运行时需要调整线路.针对以上问题及要求,配电网亟需一种无需先验物理信息和人工现场检查的智能方法来进行其无环和有环拓扑的动态生成.该方法可作为现有运行方法的辅助决策方法,进而提高其智能化程度.智能电表的普及为数据驱动的拓扑生成方法提供了新的思路和数据基础,有些学者已经提出了基于时序数据进行配电网拓扑辨识的方法. Bolognani S等[7]提出基于信息论及Chow-Liu算法来分析配电网母线电压数据关联性,但其只能生成无环路的拓扑网络. Meinshausen N等[8]从理论上论证了基于LASSO算法的邻域选择法可生成有环拓扑. Liao Y等[9]提出基于LASSO算法理论及逻辑补充规则来生成有环拓扑,但其未考虑到LASSO算法的适用条件,因此需要较复杂的逻辑与或非规则来提高精确度.
在充分考虑配电网的物理运行机理的基础上,笔者认为LASSO算法在生成电网拓扑时发生高错误率的核心原因是其输入数据存在不满足算法充分条件的情况.因此,利用电压关联分析模型构建高效简单的补充判据来规避不满足充分条件的情况,以提高LASSO算法的准确率.算法无需GIS记录信息等先验知识,仅需配电网母线的时序电压数据,即可生成无环和有环2种类型的拓扑,且具有较高的准确率和较低的计算复杂度.
1 系统模型一个台区被定义为包含若干母线和支路的物理网络,将其抽象地构建成一个图模型G=(N, S),描述节点的集合为N={1, 2, …, m},节点代表母线,描述边的集合为S={xi, j|i, j∈N},边代表支路.
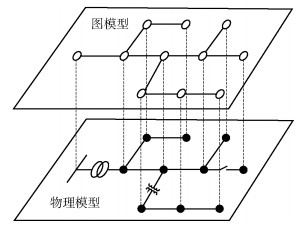
物理模型和图模型的对应关系如图 1所示.母线τ的时序量测电压数据为uτt=|uτt|ejθτt,uτt∈
|
图 1 配电网物理模型与图模型对应关系 |
基于物理模型转化的图模型,首先在融合物理机理的基础上,从概率的角度分析了母线之间的条件独立性,然后将配电网拓扑结构的生成问题转化为寻找各母线的邻域节点.算法基于以下几步实现拓扑生成:1)利用最小绝对值收敛和选择算法(LASSO, least absdute shrinkage and selection operator)算法寻找各母线的邻域节点,构成母线之间的关联系数矩阵(CCM, correlation coefficient matrix);2)利用“and”规则消除拓扑结构的方向性问题,构建无向拓扑结构;3)LASSO算法在求解复杂连接关系的关联系数向量时,存在不满足充分条件的情况,此时算法的错误率会升高.对此,提出基于关联分析模型的判据来修改CCM.笔者融合LASSO算法、“and”规则和关联分析模型的判据,设计了数据驱动的L&C算法(L&C, LASSO & correlation algorithm)生成配电网拓扑.
2.1 条件独立性分析配电网的拓扑结构分为无环和有环2种基本类型.无环网络可以抽象为树形.由于其边和节点数存在定量的关系,相对较容易生成其拓扑;而有环的结构是在树形的基础上包含了母线之间的回环连接.因此,如果没有确定其拓扑图边数等先验知识,极易造成母线间的错误连接.可知,无环拓扑的生成问题本质上是有环拓扑生成问题的子问题.因此,可直接分析有环拓扑的生成问题.
基于联合概率分布模型来描述母线之间的独立性和相关性:
| $ \begin{align} &\ \ \ \ \ \ \ \ P({{U}_{N}})=P({{U}_{2}}, {{U}_{3}}, \cdots, {{U}_{m}})= \\ &P({{U}_{2}})P({{U}_{3}}|{{U}_{2}})\cdots P({{U}_{m}}|{{U}_{2}}, \cdots, {{U}_{m-1}}) \\ \end{align} $ | (1) |
其中:UN描述整个网络各母线电压的集合,U2, U3, …, Um表示各母线的电压值.母线1是平衡节点,它是一个单位幅值和零度相位的常量,所以,U1在概率分布的公式中忽略不计,默认常量.
在配电网中,由于母线与其相邻母线的关联强度远大于与其不相邻母线的关联强度,因此,式(1)可近似为
| $ P({{U}_{N}})\simeq \prod\limits_{\tau =2}^{m}{P({{U}_{t}}|{{U}_{F(\tau )}})} $ | (2) |
其中:集合F(τ)代表母线τ的邻域集合.
在配电网中存在如下定理:如果每条母线的电流注入是近似独立的,那么各母线的时序电压与其不相邻母线的时序电压具有条件独立性[9].因此,在台区电网各母线电流注入相互独立的前提下,式(2)可看作恒等成立,即各母线仅与其相邻母线有强的统计相关性.
| $ P({{U}_{N}})\simeq \prod\limits_{\tau =2}^{m}{P({{U}_{\tau }}|{{U}_{F(\tau )}})} $ | (3) |
据此分析,拓扑生成的核心工作是找到各母线的邻域集合F(τ).因此,首先需要选取一种高效的方法来寻找各母线的邻域集合.
2.2 LASSO算法假设UN服从多元高斯混合分布,那么在给定母线τ的情况下,UN\{τ}也符合多元高斯混合分布.因此,给定母线τ时,式(3)可由混合高斯概率分布模型量化为
| ${{U}_{\tau }}=U_{N\backslash \{\tau \}}^{\text{T}}{{\beta }^{\tau }}+{{E}_{N\backslash \{\tau \}}} $ | (4) |
其中:UN\{τ}表示图中不包含母线τ的变量集合,βτ表示母线τ的关联系数向量,EN\{τ}是零均值的误差项.在向量βτ中,零元素对应的母线与母线τ不相邻,非零元素对应的母线与母线τ相邻,且元素数值的大小表示其相互之间关联程度的强弱.因此,寻找母线τ的邻域问题可以转化为计算各母线的关联系数向量βτ,换言之,寻找母线τ的邻域问题是基于时序电压数据计算母线τ与其余母线之间的多元线性回归分析问题.
典型的无环和有环的配电网拓扑结构均是非全连接的,配电网的拓扑结构图是稀疏的.假设配电网有m条母线,其中一条母线τ的邻域集合F(τ)的个数是n.则n≪m,母线τ的关联系数向量βτ是1×m的向量,βτ中有δ维元素是零,δ=m-n.因此,寻找母线τ的邻域问题本质上是要保证回归系数稀疏化的多元时序变量的线性回归问题.
一种广泛地用来确保线性回归系数稀疏的方法LASSO是一种同时进行特征选择和正则化的回归分析方法,也被叫做线性回归的L1正则化方法[10].其多元线性回归系数的求解公式为
| $ {{\overset\frown{\beta }}^{\tau }}=\underset{{{\beta }^{\tau }}\left( 1 \right)=0}{\mathop{\text{arg }\!\!~\!\!\text{ }\ \text{min}}}\, \left\{ \sum\limits_{t=1}^{N}{{{(u_{\tau }^{t}-{{(\mathit{\boldsymbol{u}}_{n\backslash \{\tau \}}^{t})}^{\text{T}}}{{\beta }^{\tau }})}^{2}}+\lambda \|{{\beta }^{\tau }}{{\|}_{1}}} \right\} $ | (5) |
其中:‖βτ‖1表示βτ的1范数,λ≥0表示惩罚项系数.
LASSO方法是在一般线性回归模型的平方误差函数的基础上增加L1范数的惩罚项,使得回归系数的求解结果稀疏化,即惩罚项系数λ的大小控制着其对应的回归系数向量中零元素的个数. λ的计算是基于母线τ及其邻域母线的时序电压的高斯分布特征,其计算过程体现了母线及其邻域母线的时序运行特征.各母线对应的参数λ是不同的,不同的参数λ控制着不同母线对应的回归系数非零元素的个数,各母线的非零元素对应着其相邻的母线.换言之,各母线的参数λ控制着其连接情况.因此,LASSO算法可应用于寻找配电网母线τ的邻域元素.
惩罚项系数λ的选择至关重要,因为它会影响β中非零系数的数量.当λ较小时,惩罚项的影响较小,可行解接近于最小二乘法的可行解.当λ较大时,β的大量系数为零,造成矩阵的过度稀疏性压缩.因此,寻找最佳的λ惩罚项系数是合理求解LASSO问题的关键,λ的求解计算公式为
| $ {{\lambda }^{\tau }}\left( \alpha \right)=\frac{2{{\overset\frown{\sigma }}_{\tau }}}{\sqrt{N}}\widetilde{\phi }{{~}^{-1}}\left( \frac{\alpha }{2{{p}^{2}}} \right) $ | (6) |
其中:通过控制虚警概率α生成最佳的λ[8],
通过求解LASSO问题,可得母线τ对应的βτ,循环计算βτ,τ={1, 2, …, m},将各母线对应的β按序构成CCM,CCM是m×m的矩阵,其大部分元素是零,因此,CCM也是稀疏的.
2.3 “and”规则由于LASSO的求解结果包含了拓扑连接的方向性问题,即母线i和j之间的关系系数βij和βji可能不同,换言之,LASSO算法的结果认为母线i和j的连接关系与母线j和i的连接关系不同.但配电网的拓扑图本质是无向图,描述母线i和j之间关联性的只应该有唯一的状态. “and”规则可保证配电网的拓扑无方向性,其规则为
| $ e_{i}^{j}=\beta _{i}^{j}\wedge \beta _{j}^{i} $ | (7) |
其中:符号∧表示逻辑与运算,即如果βij和βji中有一个为0,那么母线i和j之间的关联系数为0.
对CCM矩阵的上三角矩阵和下三角矩阵的对应元素做“and”判据运算后得到矩阵E. E是一个上三角矩阵,E中母线i和j之间的连接状态唯一.
2.4 补充判据LASSO算法在求解稀疏矩阵时要满足充分条件,否则它并不能优化收敛到唯一的可行解,因此,如果不考虑算法的充分条件,算法会存在错误计算CCM的可能性[11-12].
LASSO算法的充分条件具体可描述为,如果存在满足L0和L1范数正则化约束的唯一解,那么其L0范数的可行解个数必须存在约束为
| $ \|{{\beta }_{\tau }}{{\|}_{0}} < \frac{1}{2}\left( 1+\frac{1}{\mu \left( \mathit{\boldsymbol{A}} \right)} \right) $ | (8) |
其中:‖βτ‖0是βτ的L0范数,物理意义为母线τ的邻域集合元素个数,矩阵A =[u1, u2, …, um]∈
| $ \mu \left( \mathit{\boldsymbol{A}} \right)=\underset{1\le i, j\le m, i\ne j}{\mathop{\text{max}}}\, ~\frac{|{{u}_{i}}{{u}_{j}}|}{\|{{u}_{i}}\|\|{{u}_{j}}\|} $ | (9) |
从充分条件的表达式(8)可以看出,在求解母线邻域时,当母线邻域集合元素越多时,充分条件要求任意母线之间的最大关联度越低.当台区电网包含的母线个数越多时,各母线的邻域集合将越大,充分条件将更加难以满足.当充分条件无法满足时,拓扑生成将可能发生错误,错误大多发生在邻域元素多的母线.因此,拓扑生成需要更加严格的补充判据来保证其正确性.
为进一步提高算法的准确率,算法使用电压关联分析模型的判据作为补充判据,通过判据剔除稀疏CCM中由于不满足LASSO充分条件而计算出错的元素,从而进一步提高准确度.
电压关联分析模型从母线-支路关联矩阵入手来分析母线间的关联关系,由于支路元素的介入,相比于LASSO算法,其母线间的关系更加独立.因此,电压关联分析模型对母线的邻域集合的大小不敏感,并不会因为母线邻域集合的元素越多而发生判断的错误.电压关联分析模型性能可以较好地契合LASSO算法,作为其补充条件.
电压关联分析模型提出的判据为
| $ {{K}_{ij}}\left\{ \begin{align} &>0, \ \ \text{if}\ i=j \\ &<0,\ \ \text{if}\ i\sim j \\ &>0, \ \ \text{if}\ \ \exists \ l\in N\ \text{and}\ \ i\sim l, l\sim j \\ &=0, \ \ 其他 \\ \end{align} \right. $ | (10) |
K矩阵为m×m的对称矩阵,符号“~”表示两节点直接相连,母线i和j之间的连接性元素为Kij.如果母线i和j直接相连,则Kij<0,如果隔一个节点l相连或i=j,则Kij>0,其余情况均为0.补充判据要求“and”判据得到的元素eij必须与K矩阵的判据元素Kij一致.计算K矩阵[7]的核心方法为
| $ \begin{array}{l} \mathit{\boldsymbol{K \boldsymbol{\varLambda} }} = \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{1}}_0}{\bf{1}}{^{\rm{T}}}\\ \;\;\;\;\mathit{\boldsymbol{KI}} = 0 \end{array} $ | (11) |
其中:Λ为母线电压的协方差矩阵,I为单位矩阵,10为第一个元素是1其余元素均是0的列向量,1为全为1的列向量.
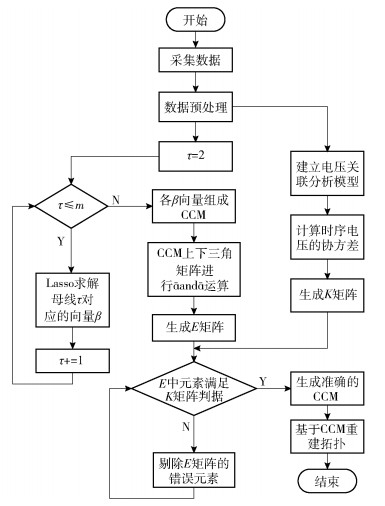
2.5 L&C算法综述综合以上分析,将拓扑生成的核心步骤总结为L&C算法.对于一个包含m条母线和观察时间点个数为T的配电网,L&C算法计算各条母线系数的时间复杂度为O(m3+Tm2),计算整体网络的时间复杂度为O(m4+Tm3).其步骤2~4与步骤5可并行进行. L&C算法描述与流程如下.
数据需求:|uτt| for τ= 2, 3, …, m, t=1, 2, …, T.
1 规范化和标准化|Us|,令其符合零均值和统一方差的分布.
2 循环计算各母线与其邻域母线的关联关系向量.
for τ=2, 3, …, m do
利用LASSO算法求解母线τ的关联关系向量
end
3 组合各母线的关联关系向量,构成CCM.
4 CCM的上三角矩阵和下三角矩阵做“and”运算,得到E矩阵.
5 计算|Us|的协方差矩阵,求解K矩阵.
6 利用K矩阵判据剔除E矩阵的错误元素.
7 CCM中非零元素对应的母线相连,生成台区电网拓扑.
|
图 2 L&C算法流程 |
基于Matlab的Matpower模块,仿真了8-bus、14-bus、33-bus、69-bus、84-bus、119-bus配电系统.为验证算法生成无环和有环网络的准确率,上述的配电系统都设置了无环和有环的网络结构.测试设置时序随机变量的有功功率pst和无功功率qst来产生各母线电压数据,它们与系统初始值pinit和qinit的比值为pst/pinit,符合均匀分布U(0.95, 1.05).设定智能电表的数据传输1次/h,仿真模拟智能电表不断生成的电压测量值.
为了统一评估L&C算法在各个模型中的表现,错误率R指标为
| $ R=~\left( \frac{\sum\limits_{{{s}_{i, j}}\in S}{1\left( {{s}_{i, j}}\notin \tilde{S} \right)}+\sum\limits_{{{s}_{i, j}}\in \tilde{S}}{1\left( {{s}_{i, j}}\notin S \right)}}{\left| S \right|} \right) $ | (12) |
其中:1(expression)表示如果表达式成立,则其返回1,S表示网络的边的集合,
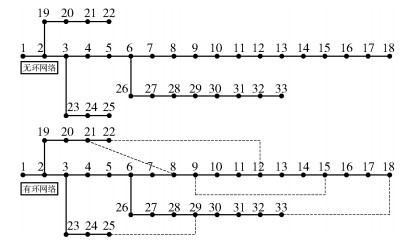
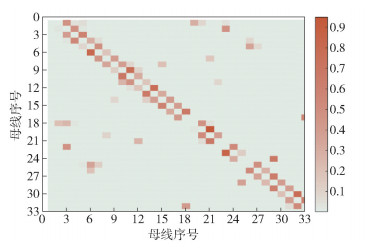
以bus-33为例,其图模型如图 3所示. L&C算法计算所得有环bus-33网络的CCM的密度如图 4所示. CCM的系数从小到大对应的色彩从白色到深橙色.从图中可以看出,不相连母线对应的关联系数均为0,相连母线对应的关联系数均大于零,且随着关联度的增强其关联系数也在增大,说明L&C算法也可以分析拓扑中各母线的关联程度.
|
图 3 无环和有环的33-bus模型 |
|
图 4 33-bus无环网络的稀疏关联系数矩阵对应的着色图 |
从表 1所示的误差率对比分析可知,在LASSO算法+ “and”规则基础上增加的补充判据是必要的和有效的.在获取相同时序长度(720个时间点)的电压数据情况下,仅通过LASSO算法和“and”判据,而不使用补充判据来生成33-bus的无环和有环的配电网拓扑结构,其误差率分别是6.45%和15.79%.增加补充判据后,算法的误差率均降低至0.实验结果说明补充判据降低了误差率,且对无环和有环的网络均适用.
|
|
表 1 算法在有无补充判据情况下的误差率 |
表 2所示为L&C算法在获取不同时序长度数据的情况下生成不同规格配电网的误差率的结果.在获取相同时间数据的情况下,如720个时间点,随着网络复杂度的提高,算法的误差率均在上升.但算法在生成同类型网络拓扑时,随着获取数据的时序变长,算法的误差率逐步下降.其原因是,在生成复杂网络时,如果输入的数据量太少,算法会存在欠拟合的问题.随着输入数据时序长度的增加,算法的拟合程度变好,误差率下降.从整体误差率分析,算法在获取一定时序电压数据的情况下,生成不同网络拓扑的误差率均较低,反映出算法具有良好的性能.
|
|
表 2 L&C算法在获取不同长度电压数据的情况下生成多类配电网拓扑的误差率 |
表 3所示为已有算法与L&C算法在获取固定时序长度720个时间点的情况下生成配电网bus-33的无环和有环拓扑结构的误差率对比结果. Chow-Liu算法只能生成树状的拓扑结构,其本身不存在环路.因此,利用该算法生成无环拓扑时误差率是0,而生成有环拓扑时误差率高达24.32%. LASSO+“and”规则的算法忽略了LASSO算法在生成拓扑结构时存在充分条件不满足的情况,其生成无环和有环的拓扑结构时均存在误差,误差率分别为6.45%和15.79%.在同等条件下,L&C算法生成2种拓扑的误差率均为0,且具有较高的准确率.实验结果说明,L&C算法在生成无环和有环2种类型的配电网拓扑结构时,综合性能良好.
|
|
表 3 L&C算法与现有算法的误差率对比 |
从实际需求的角度分析,如果已确保配电网部分拓扑信息准确,也可以使用算法进行局部的拓扑辨识,完成拓扑的更新.此外,算法也可以采用滑动窗口的模式生成拓扑,将生成的拓扑与原始拓扑对比,即可实现动态地拓扑辨识.算法可作为生成实际运行配电网拓扑的辅助决策方法.
4 结束语针对配电网存在GIS记录信息不准确、布线复杂、且易发生人为私自修改线路等情况,笔者提出了一种新型的数据驱动的配电网拓扑生成算法,实现了仅需智能配电网的各母线时序电压信息即可生成无环和有环2种类型的拓扑,且具有高准确率和较低的计算复杂度.为配电网拓扑结构的智能化管理提供了新的思路,同时也为配电网的安全稳定运行提供了新的辅助决策方法.笔者设计的L&C算法融合了机器学习的LASSO模型及其补充规则,以解决配电网的拓扑生成问题,具有一定的前沿性.
本算法是针对单源配电网重构问题,有待在进一步完善L&C算法的基础上研究多源配电网的重构问题.新型数据驱动的配电网拓扑生成技术是智能电网研究的重要内容.
| [1] |
马钊, 周孝信, 尚宇炜, 等. 未来配电系统形态及发展趋势[J]. 中国电机工程学报, 2015, 35(6): 1289–1298.
Ma Zhao, Zhou Xiaoxin, Shang Yuwei, et al. Form and development trend of future distribution system[J]. Proceedings of the CSEE, 2015, 35(6): 1289–1298. |
| [2] | Clement-Nyns K, Haesen E, Driesen J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371–380. doi: 10.1109/TPWRS.2009.2036481 |
| [3] |
周苏荃, 柳焯. 新息图法识别多重网络结构动态变化[J]. 中国电机工程学报, 2001, 21(10): 67–72.
Zhou Suquan, Liu Zhuo. Identification of multiple dynamic network structure changes by the innovation graph approach[J]. Proceedings of the CSEE, 2001, 21(10): 67–72. doi: 10.3321/j.issn:0258-8013.2001.10.016 |
| [4] | Sun Hongbin, Gao Feng, Zhang Boming, et al. Application of minimum information loss based state estimation to topology error identification[J]. Proceedings of the CSEE, 2005, 25(18): 1–5. |
| [5] | Muscas C, Pau M, Pegoraro P A, et al. An efficient method to include equality constraints in branch current distribution system state estimation[J]. Eurasip Journal on Advances in Signal Processing, 2015, 2015(1): 17. doi: 10.1186/s13634-015-0206-1 |
| [6] |
陈艳波, 何光宇, 周京阳, 等. 基于改进转移潮流法的拓扑错误辨识方法[J]. 电网技术, 2012, 36(3): 95–100.
Chen Yanbo, He Guangyu, Zhou Jingyang, et al. An improved power flow transfer approach with enhanced ability to identify topology error and bad data[J]. Power System Technology, 2012, 36(3): 95–100. |
| [7] | Bolognani S, Bof N, Michelotti D, et al. Identification of power distribution network topology via voltage correlation analysis[C]//IEEE Conference on Decision and Control. Florence: IEEE, 2013: 1659-1664. |
| [8] | Meinshausen N, Bühlmann P. High-dimensional graphs and variable selection with the LASSO[J]. Annals of Statistics, 2006, 34(3): 1436–1462. doi: 10.1214/009053606000000281 |
| [9] | Liao Y, Weng Y, Rajagopal R. Urban distribution grid topology reconstruction via LASSO[C]//Power and Energy Society General Meeting. Boston: IEEE, 2016: 1-5. |
| [10] | Jones M C, Pewsey A. Bayesian LASSO regression[J]. Biometrika, 2009, 96(4): 835–845. doi: 10.1093/biomet/asp047 |
| [11] | Elad M, Bruckstein A M. A generalized uncertainty principle and sparse representation in pairs of bases[J]. IEEE Transactions on Information Theory, 2002, 48(9): 2558–2567. doi: 10.1109/TIT.2002.801410 |
| [12] | Donoho D L, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via L1 minimization[J]. Proceedings of the National Academy of Sciences, 2003, 100(5): 2197–2202. doi: 10.1073/pnas.0437847100 |


