为了准确地预测链路质量,提出基于改进最小二乘支持向量回归机的无线传感器网络链路质量预测模型.采用粗糙集理论约简链路质量参数,以提取出有效反映链路质量的特征参数;利用遗传算法优化最小二乘支持向量回归机的惩罚因子和核函数宽度.实验结果表明,与Experts Advice预测模型相比,提出的预测模型具有更高的精度.
In order to predict the link quality accurately, a link quality prediction model was proposed to predict link quality for sensor networks based on improved least square support vector regression machine (LS-SVR). The rough set (RS) was introduced to reduce the link quality metrics so as to extract the effective characteristic metrics of the link quality. And the genetic algorithm (GA) was employed in LS-SVR to optimize the penalty factor and kernel width. Experiments show that compared with the experts advice-based prediction model, the proposed prediction model achieves better accuracy.
无线传感器网络(WSNs, wireless sensor networks)是由能量受限的节点通过无线自组织方式形成的分布式系统,节点可随机部署在监测区域,应用于军事、医疗、环境监测[1]等领域.选择高质量的链路传输数据,可减少节点能量损耗、提高网络数据吞吐率.有效的链路质量预测模型能够准确地预判链路状况,为路由协议(CTP、AODV、QHCR[2]等)选择稳定、可靠的链路提供依据,从而提高网络的整体性能.
WSNs链路质量预测方法主要包括基于通信链路特性、基于概率估计和基于智能学习3类方法.基于通信链路特性的预测方法涉及的链路评估物理层参数包括接收信号强度指标(RSSI, received signal strength indicator)、链路质量指标(LQI, link quality indicator)、信噪比(SNR, signal-to-noise ratio)等,涉及的数据链路层参数有包接收率(PRR, packet reception ratio)等;基于概率估计的预测方法从概率论的角度对包接收率进行预测;基于智能学习的预测方法主要有FLI[3]、Experts Advice[4]、FSVR[5]、Gillbert-Elliot[6]等方法.
采用卡尔曼滤波和粗糙集理论(RS, rough set)对链路质量参数集进行预处理;采用遗传算法(GA, genetic algorithm)优化最小二乘支持向量回归机(LS-SVR, least squares support vector regression)的惩罚因子和核函数宽度,得到链路质量预测模型(GA-SVR, least squares support vector regression based on genetic algorithm).
1 链路质量参数的预处理为了避免外界因素对链路质量参数的干扰,采用卡尔曼滤波(Kalman filter)方法对原始数据集进行降噪,形成决策表;采用RS对决策表进行约简,得到最小条件属性集,作为链路质量预测的样本集.
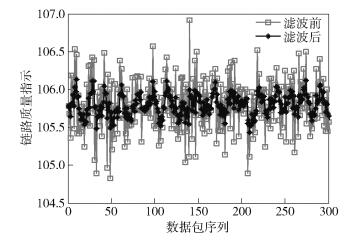
1.1 降噪采用文献[7]中的降噪方法,对实验采集到的物理层参数RSSI、LQI和SNR分别进行降噪处理,其中对室内走廊中原始LQI降噪处理的效果如图 1所示.
|
图 1 降噪前、后LQI的对比 |
由图 1可知,降噪后的LQI波动范围有明显的减小,降低了噪声对参数的影响.
1.2 知识约简信息系统S=〈U, A, V, f〉,其中U为有限个对象的集合,U={x1, x2, …xn},n为实测数据的组数,
基于知识约简的粗计算是粗糙集理论得以实际应用的关键.设
| $ \underline P \left( X \right) = \left\{ {Y \in U\left| {P:Y \subseteq X} \right.} \right\} $ | (1) |
| $ \bar P\left( X \right) = \left\{ {Y \in U\left| {P:Y \cap X \ne \emptyset } \right.} \right\} $ | (2) |
| $ {\gamma _P}\left( X \right) = \left| {\underline P \left( X \right)} \right|/\left| X \right| $ | (3) |
| $ {\rm{Bn}}{{\rm{d}}_P}\left( X \right) = \bar P\left( X \right) - \underline P \left( X \right) $ | (4) |
其中|X|为集合X的势,即集合中所含元素个数.
设室内走廊信息系统S上的一个分类为ψ[8],经约简后的最小条件属性子集R={RSSI, LQI},与原始条件属性集C={RSSI, LQI, SNR}有相同的分类质量,即γR(ψ)=γC(ψ).类似地,得到校内树林信息系统中的约简结果为{RSSI, SNR},校内广场信息系统中的约简结果为{RSSI, SNR}.
2 链路质量预测LS-SVR利用二次损失函数取代传统支持向量机中不敏感的损失函数,将传统支持向量机中的不等式约束条件改写成等式约束. LS-SVR具有运算简单、收敛速度快的优点[9],采用LS-SVR[10]建立链路质量预测模型.
2.1 LS-SVR给定约简后的样本集T为
| $ T = \left\{ {\left( {{\mathit{\boldsymbol{x}}_1},{y_1}} \right), \cdots ,\left( {{\mathit{\boldsymbol{x}}_m},{y_m}} \right)} \right\} \in \left( {{R^n} \times R} \right) $ | (5) |
其中:xi∈Rn, yi∈R, i=1, 2,…, m.
LS-SVR通过非线性映射
| $ y\left( \mathit{\boldsymbol{x}} \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\phi \left( \mathit{\boldsymbol{x}} \right) + b $ | (6) |
其中:w为权重向量,
| $ \left. \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{w}},b,\xi } J\left( {\mathit{\boldsymbol{w}},\xi } \right) = \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w + }}\frac{g}{2}\sum\limits_{i = 1}^m {\xi _i^2} \\ {\rm{s}}.\;{\rm{t}}.\;\;{y_i} = {\mathit{\boldsymbol{w}}^{\rm{T}}}\phi \left( {{\mathit{\boldsymbol{x}}_i}} \right) + b + {\xi _i},i = 1,2, \cdots ,m \end{array} \right\} $ | (7) |
其中:g为惩罚因子,ξi为xi的松弛系数, ξ=(ξ1, ξ2, …, ξm).为求得目标函数的最小值,构造拉格朗日(Lagrange)函数为
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\boldsymbol{w}},b,\xi ,\mathit{\boldsymbol{\alpha }}} \right) = J\left( {\mathit{\boldsymbol{w}},\xi } \right) - }\\ {\sum\limits_{i = 1}^m {{\alpha _i}\left[ {{\mathit{\boldsymbol{w}}^{\rm{T}}}\phi \left( {{\mathit{\boldsymbol{x}}_i}} \right) + b + {\xi _i} - {y_i}} \right]} } \end{array} $ | (8) |
其中:α=(α1, …, αm).为求得最优解,可根据KKT(Karush-Kuhn-Tucker)条件[10]将w和ξi消去,则上述求解的优化问题可转化为线性方程
| $ \left( {\begin{array}{*{20}{c}} 0&{{\mathit{\boldsymbol{Q}}^{\rm{T}}}}\\ \mathit{\boldsymbol{Q}}&{\mathit{\boldsymbol{H}} + {g^{ - 1}}\mathit{\boldsymbol{I}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} b\\ {{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0\\ \mathit{\boldsymbol{y}} \end{array}} \right) $ | (9) |
其中:
基于LS-SVR的链路质量预测模型为
| $ y\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^m {{\alpha _i}K\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_i}} \right) + b} $ | (10) |
通过核函数K(x, xi)将具有高维非线性特点的数据样本映射至高维特征空间中,在低维空间中求得最优回归模型.采用径向基核函数作为理想的选择,决策函数
| $ y\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^m {{\alpha _i}\exp \left\{ { - \frac{{{{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right\|}^2}}}{{2{z^2}}}} \right\} + b} $ | (11) |
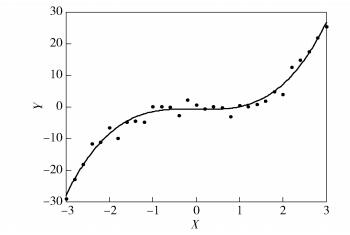
其中:z为核函数宽度. LS-SVR在二维空间中的拟合效果如图 2所示.
|
图 2 二维空间中的拟合效果 |
GA具有优化精度高、收敛速度快的优点.采用GA对LS-SVR中的惩罚因子g和核函数宽度z进行优化.
采用均方误差(MSE, mean square error)[11]统计预测值和观测值之间的误差为
| $ e = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {f\left( {{\mathit{\boldsymbol{x}}_i}} \right) - {y_i}} \right)}^2}} $ | (12) |
为提高预测精度,在适值函数中考虑MSE,适值函数的定义为
| $ {\rm{Fit}}\left( {g,2{z^2}} \right) = \frac{N}{e} $ | (13) |
其中:N为设定的最大遗传代数.遗传算法中的选择算子Ok为
| $ {O_k} = \frac{{{\rm{Fit}}\left( {g,2{z^2}} \right)}}{{\sum {{\rm{Fit}}\left( {g,2{z^2}} \right)} }} $ | (14) |
GA-SVR链路质量预测模型分为训练阶段和测试阶段.
训练阶段,设定迭代次数为200、精度为1×10-6,利用式(14)求得室内走廊、校内树林和校内广场3个场景中的(g, 2z2)分别为(1.3138, 0.3030),(0.7616, 15.0000)和(1.1566, 9.5665);利用约简后的样本集训练LS-SVR模型,得到回归机的相关参数α和b.
测试阶段,将未知状态的特征数据处理成数字特征向量形式.由1.2节的约简结果可知,室内走廊环境下的输入向量为(
实验场景如图 3所示,选用CrossBow公司的TelosB节点收集数据,在自主研发的无线传感网络链路质量测试平台(WSNs-LQT, wireless sensor networks link quality testbed)上进行分析.

|
图 3 实验场景 |
实验参数设置如表 1所示.
|
|
表 1 链路质量测试参数设置情况 |
相关性分析可以了解参数间的密切程度,其中皮尔逊(Pearson)相关系数是对定距变量的数据进行计算,如式(15)所示.
| $ r = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} \sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } }} $ | (15) |
其中:r为相关系数,
采用统计软件SPSS计算降噪后各个链路质量参数间的Pearson相关系数,3个场景下的相关性分别如表 2~4所示.
|
|
表 2 室内走廊各度量参数间的相关性 |
|
|
表 3 校内树林各度量参数间的相关性 |
|
|
表 4 校内广场各度量参数间的相关性 |
室内走廊环境下,RSSI、LQI和SNR与PRR之间的相关系数均高于校园树林环境和校园广场环境.与室内走廊环境相比,校内广场环境下LQI与PRR间的相关系数下降了0.592;与校内树林环境相比,广场环境下LQI与PRR间的相关系数下降了0.490,LQI受环境影响较大.因此,选择RSSI和LQI为室内走廊环境下的链路质量预测样本集;校内树林环境和校内广场环境下选择RSSI与SNR为链路质量预测的样本集.
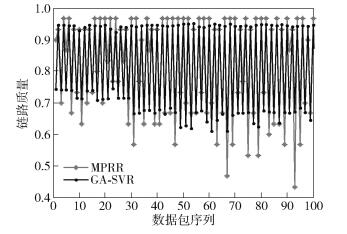
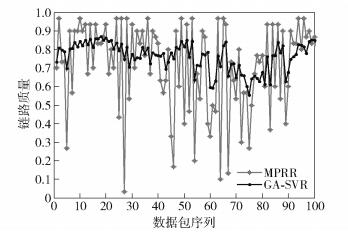
3.3 结果分析3个场景下,PRR的实测值(MPRR,measured packet reception ratio)与GA-SVR预测模型的预测值分别如图 4~6所示.
|
图 4 室内走廊误差对比 |
|
图 5 校内树林误差对比 |
|
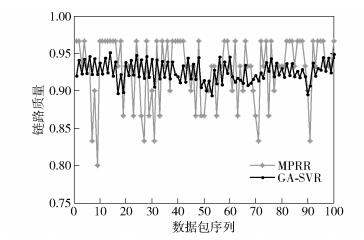
图 6 校内广场误差对比 |
采用MSE评价链路质量预测的效果,3个场景下GA-SVR预测模型的MSE如表 5所示.
|
|
表 5 3个场景下的MSE |
GA-SVR预测模型能比较好地贴近实测PRR,当PRR观测值变化幅度较大时,GA-SVR预测模型能很好地捕捉到这一变化,具有很高的预测精度.
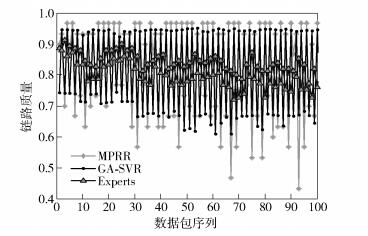
3.4 与其他方法的对比GA-SVR预测模型与Experts Advice预测模型[5]的预测性能对比如图 7所示.
|
图 7 预测性能对比 |
由图 7可知,GA-SVR预测模型的预测结果更贴近实测PRR值,2种方法的MSE如表 6所示,显然,GA-SVR预测模型的预测精度高于Experts Advice预测模型.
|
|
表 6 GA-SVR模型与Experts Advice模型的MSE |
针对随机部署的无线传感器网络,采用卡尔曼滤波方法对链路质量参数进行降噪,形成决策表;采用粗糙集理论对决策表进行约简,得到最小样本集;提出GA-SVR链路质量预测模型.与Experts Advice预测模型相比,GA-SVR预测模型具有更高的预测精度.下一步工作将对链路质量参数进一步研究,以找出能更全面、准确刻画链路状态的参数.
| [1] |
潘成, 张和生. 无线传感器网络快速数据收集的聚集调度方法[J]. 北京邮电大学学报, 2016, 39(4): 87–91.
Pan Cheng, Zhang Hesheng. Fast data collection of wireless sensor networks by aggregation scheduling[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(4): 87–91. |
| [2] | Amjad M, Afzal M K, Umer T, et al. QoS-aware and heterogeneously clustered routing protocol for wireless sensor networks[J]. IEEE Access, 2017, 39(99): 1–12. |
| [3] |
郭志强, 王沁, 万亚东, 等. 基于综合性评估的无线链路质量分类预测机制[J]. 计算机研究与发展, 2013, 50(6): 1227–1238.
Guo Zhiqiang, Wang Qin, Wan Yadong, et al. A classification prediction mechanism based on comprehensive assessment for wireless link quality[J]. Journal of Computer Research and Development, 2013, 50(6): 1227–1238. doi: 10.7544/issn1000-1239.2013.20121299 |
| [4] | Marinca D, Minet P. On-line learning and prediction of link quality in wireless sensor networks[C]//2014 IEEE Global Communications Conference (GLOBECOM). Austin: IEEE Press, 2014: 1245-1251. |
| [5] |
舒坚, 汤津, 刘琳岚, 等. 基于模糊支持向量回归机的WSNs链路质量预测[J]. 计算机研究与发展, 2015, 52(8): 1842–1851.
Shu Jian, Tang Jin, Liu Linlan, et al. Fuzzy support vector regression-based link quality prediction model for wireless sensor networks[J]. Journal of Computer Research and Development, 2015, 52(8): 1842–1851. doi: 10.7544/issn1000-1239.2015.20140670 |
| [6] | Bildea A, Alphand O, Rousseau F, et al. Link quality estimation with the Gibert-Elliot model for wireless sensor networks[C]//2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (2015 PIMRC). Hong Kong: IEEE Press, 2015: 2049-2054. |
| [7] | Shu Jian, Tao Juan, Liu Linlan, et al. CCI-based link quality estimation mechanism for wireless sensor networks under non-perceived packet loss[J]. The Journal of China Universities of Posts and Telecommunications, 2013, 20(1): 1–10. doi: 10.1016/S1005-8885(13)60001-1 |
| [8] |
赵斌, 何泾沙, 张伊璇, 等. 访问控制中基于粗糙集的授权规则指示发现[J]. 北京邮电大学学报, 2016, 39(2): 48–52.
Zhao Bin, He Jingsha, Zhang Yixuan, et al. Knowledge discovery of authorization rule based on rough set in trust based access control[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(2): 48–52. |
| [9] | Eberts M, Steinwart I. Optimal learning rates for least squares SVMs using Gaussian kernels[C]//2011 Annual Conference on Neural Information Processing Systems (2011NIPS). Granada: Advances in Neural Information Processing Systems, 2011: 1539-1547. |
| [10] | Ning Kefeng, Liu Min, Dong Mingyu, et al. Robust LS-SVR based on variational Bayesian and its application[C]//2014 International Joint Conference on Neural Networks (IJCNN). Beijing: IEEE Press, 2014: 2920-2926. |
| [11] | Tang Yizhou, Zhou Jiawen. The performance of PSO-SVM in inflation forecasting[C]//2015 12th International Conference on Service Systems and Service Management (ICSSSM). Guangzhou: IEEE Press, 2015: 1-4. |


