针对小小区间的同频干扰与用户异频扫描的能耗问题,提出一种基于到达时间(TOA)指纹数据库与同步参考信号(PSS/SSS)灵活传输的小小区发现策略.通过减少用户大量无效异频扫描次数,以达到节能的目的.同时,网络端对小小区基站(SBSs)PSS/SSS的发送进行控制,以降低小小区间PSS/SSS的同频干扰.仿真结果表明,所提方案能有效提高小小区的检测率和用户能效.
Densely deployed small cells suffer from the problem of severe co-channel interference among the neighbouring cells and user equipments (UEs) in the network are confronted with a challenge of intensive energy consumption in inter-frequency scanning (IFS). In order to deal with the problems, a time of arrival (TOA) fingerprint database based small cell discovery strategy was proposed, where the synchronization reference signals (primary synchronization signal/secondary synchronization signal, PSS/SSS) of small cells are transmitted in a flexible scheme. The proposed method achieves the purpose of energy saving for UE by tremendously reducing the number of invalid inter-frequency detection. Meanwhile, it is capable of alleviating the co-channel interference of synchronization signals among small cells through flexible control of PSS/SSS transmission. Simulation shows that the proposed method can effectively improve the probability of detecting small cells and the energy efficiency of UEs in the network.
与传统网络部署场景相比,密集异构网络下的小小区发现过程主要面临2个挑战:1)用户(UE, user equipment)的异频扫描(IFS, inter-frequency scanning)能耗随着网络中小小区数目的增加而急剧增大[1-2];2)小小区间同步信号与参考信号的严重同频干扰[3].针对上述问题,现有的小小区发现方案主要分为灵活的用户IFS机制和提高同步参考信号(PSS/SSS, primary synchronization signal/secondary synchronization signal)检测性能两类.其中,灵活的IFS机制能有效地提高UE的IFS能效[4-6],但存在过程复杂,信息交互量大等问题,且未能抑制小小区间PSS/SSS的同频干扰.有关提高PSS/SSS检测性能的小小区发现方案可有效提高小小区正确检测率[7-8],但存在应用局限性与频谱资源浪费等问题.
为同时解决小小区间PSS/SSS的同频干扰和UE的IFS能耗过高问题,提出一种基于TOA(time of arrival)指纹数据库与PSS/SSS灵活传输的小小区发现方案.该方案通过对每个小小区边缘覆盖区域建立TOA位置指纹信息数据库与指纹匹配过程,减少UE大量无效的IFS次数,以达到UE节能目的.与此同时,网络端对小小区基站(SBSs, small cell base stations)的PSS/SSS发送进行控制,当存在UE满足IFS要求时,网络端将命令相应的SBSs配置并发送PSS/SSS,反之不发送,从而达到降低小小区间PSS/SSS同频干扰的目的.
1 系统模型考虑小小区与宏小区异频部署的密集异构网络场景,其中宏小区工作在低频段(< 2.5GHz),小小区占用高频段(>3GHz).假设网络中存在W个小小区,构成小小区(亦即SBSs)集合S,V个宏小区,构成宏小区集合H. SBSs随机部署在网络覆盖区域,令UE集合为U,且UE在网络中的物理位置服从空间泊松点过程. UE k在t时刻对应于小小区为S(i)的信干噪比(SINR,signal to interference plus noise ratio)定义为
| $ {\Upsilon _{k,i,t}} = \frac{{{P_i}{G_{k,i}}}}{{\sum\limits_{j \in S_t^a\backslash i} {{P_j}{G_{k,j}} + {N_0}{B_{\rm{s}}}} }} $ | (1) |
其中:Gk, i为SBS i与UE k间的信道增益,Sta为时刻t发送PSS/SSS的小小区集合,Sta\i表示将集合Sta中第i个元素删除,N0为噪声功率谱密度,Bs为小小区的带宽值. UE完成一次IFS的能耗包括信道测量(Em)与解码广播信号(Ed)所消耗的能量,则一次IFS的总能耗Etot为[4]
| $ {E_{{\rm{tot}}}} = {E_{\rm{m}}} + {E_{\rm{d}}} $ | (2) |
为了能很好地分析问题,假设小小区的覆盖区域为半径为Rs的圆形区域.定义UE位置指纹信息匹配误差限度β=2r/vl,其中:vl为电磁波传播速度,r表示网络端进行指纹匹配时所能容忍的误差范围所对应的圆形地理区域半径[5].
2 基于TOA指纹数据库与同步参考信号灵活传输的小小区发现 2.1 指纹数据库的建立利用宏小区特殊参考信号(CRS, cell specific reference signal)到达UE时间(亦即TOA)构建指纹数据库,并进行UE位置信息的获取. CRS在LTE体系中的作用为接收信号质量测量与同步追踪,UE可以利用其同步追踪过程提取宏小区对应CRS的TOA值.因此,UE可在不增加系统额外开销情况下获取TOA指纹信息.根据网络部署情况,预先建立一个空指纹数据库F,其包含W个指纹数据块,每个指纹数据块是由一个小小区所有指纹点对应的指纹信息数据集构成.表 1展示了指纹数据块结构,其中,N(3≤N≤V)表示作为定位参考的宏基站数目. F{i}(i=1, 2, …, W)表示小小区i对应的指纹数据块Bi.每个指纹数据块分别以相应的小区ID进行标识,且每个指纹数据块包含M条指纹信息,分别对应M个指纹点.在每个小小区边缘区域均匀地选取M个指纹点.离线阶段,在每个指纹点进行位置指纹信息测量,将所测量的指纹信息根据指纹点所在的小区ID,将其保存至指纹数据相应的指纹数据块中,进而形成一个包含W个指纹数据块的指纹信息数据库.
| $ F = \left\{ {{B_1},{B_2}, \cdots ,{B_W}} \right\} $ | (3) |
| $ {B_i} = \left\{ {{f_1},{f_2}, \cdots ,{f_W}} \right\} $ | (4) |
|
|
表 1 指纹数据块FPbi (IDi) |
假设网络中每个SBS的PSS/SSS配置与发送均受网络端控制,即当SBSs收到网络端的指令时才配置并发送PSS/SSS;否则不发送. SBSs每次发送PSS/SSS的时长为ts,其可保证UE完成一次小小区发现过程. UE在位与小小区建立连接时,以T为周期进行同频检测,检测内容包括宏小区ID和与之相应CRS的TOA值.令指纹数据库保存在网络端,UE周期性地将同频检测结果fu上报至网络端,并与事先建立的指纹数据库F进行指纹匹配,如
| $ \left( {{i^ * },{j^ * }} \right) = \mathop {\arg \min }\limits_{\begin{array}{*{20}{c}} {i \in \left( {1,2, \cdots ,W} \right)}\\ {j \in \left( {1,2, \cdots ,M} \right)} \end{array}} \sqrt {\sum\limits_{n = 1}^N {{{\left( {{f_{\rm{u}}}\left( n \right) - F\left\{ {i,j} \right\}\left( n \right)} \right)}^2}} } $ | (5) |
| $ \delta = \frac{1}{N}\sqrt {\sum\limits_{n = 1}^N {{{\left( {{f_{\rm{u}}}\left( n \right) - F\left\{ {{i^ * },{j^ * }} \right\}\left( n \right)} \right)}^2}} } < \beta $ | (6) |
其中:F{i*, j*}为指纹数据块Bi*中第j*条指纹,fu(n)表示UE当前指纹信息第n个指纹特征值,F{i*, j*}(n)为指纹块Bi*中第j*条指纹的第n个指纹特征值.
若F{i*, j*}满足式(6),则意味着fu与指纹数据库中的指纹项匹配成功;反之匹配失败.在UE匹配成功的情况下,网络端根据与之匹配的指纹项所在指纹数据块Bi*确定该UE当前的目标小区ID.接着,网络端发送指令至相应的SBS,通知其配置并发送PSS/SSS,与此同时,触发该UE进行IFS. UE在与小小区建立连接后将不再进行低频检测,当UE与小小区断开连接时,则继续进行低频检测与上报过程.
2.3 PSS/SSS干扰抑制在传统的LTE系统机制中,每个SBS均以一定周期持续发送PSS/SSS.然而,在小小区密集部署的情况下,传统的PSS/SSS传输机制显然会导致小小区间PSS/SSS的严重同频干扰.在所提方案中,网络系统中所有SBSs的PSS/SSS发送均受到网络端控制,且采用灵活的传输方式,因此在某一时间段,网络中只有小部分SBSs会同时发送PSS/SSS.下面对某个UE在同频检测周期内,同时发送PSS/SSS的SBSs数目进行数学建模与分析.
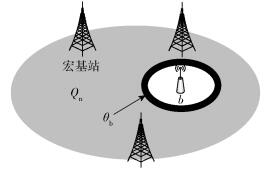
假设UE的位置服从强度为λu的空间泊松点过程.如图 1所示,令网络的覆盖区域为Qn,面积为|Qn|.定义小小区b对应的触发UE进行IFS的地理区域为
| $ \left| {{\theta _b}} \right| = \left( {R_{\rm{s}}^2 - {{\left( {{R_{\rm{s}}} - \sqrt 3 r} \right)}^2}} \right){\rm{ \mathsf{ π} }} $ | (7) |
|
图 1 概率模型示意图 |
其中Rs为小小区的覆盖半径.令A(θb)表示位于小小区b边缘覆盖区域θb内的UE数目,假设网络中的UE数目不限.由上述分析可得,对于任意θb,
| $ A\left( {{\theta _b}} \right) \sim {\rm{Poisson}}\left( {{\lambda ^{\rm{u}}}\left| {{\theta _b}} \right|} \right) $ | (8) |
根据泊松点过程性质有
| $ P\left( {A\left( {{\theta _b}} \right) \ge 1} \right) = {\lambda ^{\rm{u}}}\left| {{\theta _b}} \right| + o\left( {\left| {{\theta _b}} \right|} \right) $ | (9) |
| $ P\left( {A\left( {{\theta _b}} \right) = \chi } \right) = \frac{{{{\rm{e}}^{ - {\lambda ^{\rm{u}}}\left| {{\theta _b}} \right|}}{{\left( {{\lambda ^{\rm{u}}}\left| {{\theta _b}} \right|} \right)}^\chi }}}{{\chi !}} $ | (10) |
其中:P(C)表示事件C发生的概率值大小,χ为处于区域θb内的UE数目.对任意θb,
| $ P\left( {A\left( {{\theta _b}} \right) = 1\left| {A\left( {{Q_{\rm{n}}}} \right) = 1} \right.} \right) = \frac{{\left| {{\theta _b}} \right|}}{{\left| {{Q_{\rm{n}}}} \right|}} $ | (11) |
其中:P(*|*)为条件概率表达形式,A(Qn)表示网络范围内总的UE数目.证明过程如下:
| $ \begin{array}{*{20}{c}} {P\left( {\frac{{A\left( {{\theta _b}} \right) = 1}}{{A\left( {{Q_n}} \right) = 1}}} \right) = \frac{{P\left( {A\left( {{\theta _b}} \right) = 1,A\left( {{Q_n}} \right) = 1} \right)}}{{A\left( {{Q_n}} \right) = 1}} = }\\ {\frac{{P\left( {A\left( {{\theta _b}} \right) = 1,A\left( {{Q_n}\backslash {\theta _b}} \right) = 0} \right)}}{{A\left( {{Q_n}} \right) = 1}} = }\\ {\frac{{{{\rm{e}}^{ - {\lambda ^{\rm{u}}}\left| {{\theta _b}} \right|}}{\lambda ^{\rm{u}}}\left| {{\theta _b}} \right|{{\rm{e}}^{ - {\lambda ^{\rm{u}}}\left| {{Q_{\rm{n}}}\backslash {\theta _b}} \right|}}}}{{{{\rm{e}}^{ - {\lambda ^{\rm{u}}}\left| {{Q_{\rm{n}}}} \right|}}{\lambda ^{\rm{u}}}\left| {{Q_{\rm{n}}}} \right|}} = \frac{{\left| {{\theta _b}} \right|}}{{\left| {{Q_{\rm{n}}}} \right|}}} \end{array} $ | (12) |
进而可知,在A(Qn)=K的情况下,对A(θb)=χ,且χ=0, 1, 2, …, K有
| $ P\left( {\frac{{A\left( {{\theta _b}} \right) = \chi }}{{A\left( {{Q_{\rm{n}}}} \right) = K}}} \right) = \left( {\begin{array}{*{20}{c}} \chi \\ K \end{array}} \right){\left( {\frac{{\left| {{\theta _b}} \right|}}{{\left| {{Q_{\rm{n}}}} \right|}}} \right)^\chi }{\left( {1 - \frac{{\left| {{\theta _b}} \right|}}{{\left| {{Q_{\rm{n}}}} \right|}}} \right)^{K - \chi }} $ | (13) |
其中:
| $ {\mathit{\Gamma }_b} \sim B\left( {K,\frac{{\left| {{\theta _b}} \right|}}{{\left| {{Q_{\rm{n}}}} \right|}}} \right) $ | (14) |
其中,Γb表示事件:在A(Qn)=K的条件下A(θb)=χ,且Γb服从式(13)所示的二项分布.基于上述分析,在网络UE数为K的条件下,对于区域θb存在UE的理论概率值为
| $ P\left( {\frac{{1 \le \chi \le K}}{{A\left( {{Q_{\rm{n}}}} \right) = K}}} \right) = \sum\limits_{1 \le \chi \le K} {\left( {\begin{array}{*{20}{c}} \chi \\ K \end{array}} \right){{\left( {\frac{{\left| {{\theta _b}} \right|}}{{\left| {{Q_{\rm{n}}}} \right|}}} \right)}^\chi }{{\left( {1 - \frac{{\left| {{\theta _b}} \right|}}{{\left| {{Q_{\rm{n}}}} \right|}}} \right)}^{K - \chi }}} $ | (15) |
令网络中不同区域θb的面积大小均相等,即|θ1|=|θ2|=…=|θW|=D,则有
| $ P\left( {{\mathit{\Omega }_1}} \right) = P\left( {{\mathit{\Omega }_2}} \right) = \cdots = P\left( {{\mathit{\Omega }_W}} \right) = {P_K} $ | (16) |
| $ {P_K} = \sum\limits_{1 \le \chi \le K} {\left( {\begin{array}{*{20}{c}} \chi \\ K \end{array}} \right){{\left( {\frac{D}{{\left| {{Q_{\rm{n}}}} \right|}}} \right)}^\chi }{{\left( {1 - \frac{D}{{\left| {{Q_{\rm{n}}}} \right|}}} \right)}^{K - \chi }}} < 1 $ | (17) |
其中,Ωb表示事件:在A(Qn)=K的条件下,区域θb存在UE,即A(θb)=χ>0.由于不同小小区b之间对应的事件Ωb是相互独立的,根据所提方案中SBSs的PSS/SSS配置与发送机制可知,在小小区数目为W,UE数为K的条件下,某一时刻发送PSS/SSS的SBSs个数φ可近似为φ=PKW < W.
由上述分析可知,在UE某一同频检测周期内,所提方案中发送PSS/SSS的SBSs数小于网络中的SBSs总数,进而可知,所提方案能有效抑制小小区间PSS/SSS的同频干扰.
3 仿真验证与分析 3.1 仿真场景与参数设置仿真场景为密集异构网络,包含3个宏小区,在整个网络覆盖范围内随机分布40~180个SBSs.宏小区与小小区对应的路径损耗模型分别为[5]
| $ {L_1} = 128.1 + 37.6\lg \left( R \right) $ | (18) |
| $ {L_2} = 140.1 + 36.7\lg \left( R \right) $ | (19) |
其中:R为收发两端的距离,单位为km,详细的系统参数如表 2所示[4-5].根据文献[4],Em和Ed的大小设为1.5mJ与0.75mJ,且UE位置指纹信息匹配误差控制在半径r=5m的圆内[5].
|
|
表 2 仿真参数 |
为方便仿真结果的分析说明,做如下设置.
方案1 传统的小区发现机制.
方案2 基于TOA指纹数据库的小小区发现方案.该方案利用TOA建立数据库,UE在未与小小区建立有效连接时,周期性进行同频检测与上报过程,网络端通过指纹匹配过程触发UE进行IFS,其中,SBSs持续周期性发送PSS/SSS.
方案3 笔者所提方案.
3种小小区发现方案对应UE的IFS能耗对比如图 2所示.

|
图 2 3种小小区发现方案对应UE的IFS能耗对比 |
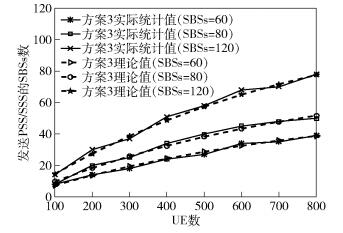
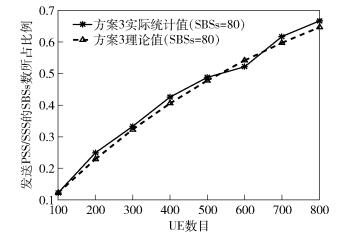
从图 2可看出,方案2和方案3相比于方案1能大幅度降低UE的IFS能耗.特别地,当IFS周期为80ms时,方案2和方案3对应UE的IFS能耗不足方案1的2%.由图 3可知,方案3中发送PSS/SSS的SBSs数目随着UE数目的增加而增大,且其实际统计值与理论值大小基本保持一致.其原因在于,随着UE数目的增大,网络中每个SBS发送PSS/SSS的概率值PK也随之增大.从图 3亦可看出,随着SBSs数目的增加,发送PSS/SSS的SBSs数目也随之增加.从图 4可见,随着UE数目的增加,网络中发送PSS/SSS的SBSs比率也随之增大,且在UE数目较小的情况下(< 600),网络中发送PSS/SSS的SBSs所占比例不足50%.由此可知,所提方案能有效抑制小小区间PSS/SSS的同频干扰.
|
图 3 发送PSS/SSS的SBSs数 |
|
图 4 发送PSS/SSS的SBSs所占比例 |
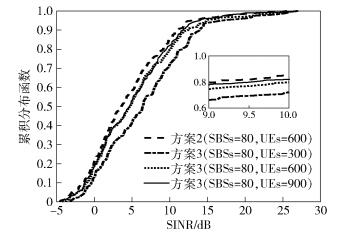
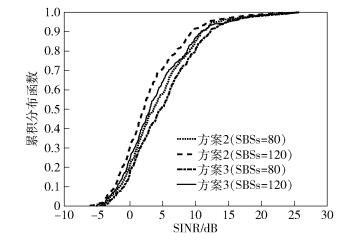
由图 5可知,方案3在不同UE数情况下,UE对应的SINR值均高于方案2.在方案3中,由于SBSs是采用灵活的PSS/SSS传输机制,在同一时间段,只有很小部分SBSs会发送PSS/SSS,因此能有效降低小小区间的PSS/SSS干扰.相反,在方案2中,SBSs是持续周期性地发送PSS/SSS,在任意时间段内所有小小区间都会产生PSS/SSS同频干扰.图 6表明,在方案2与方案3中,随着小小区数目的增加,小小区间的同频干扰会更加严重,致使UE接收PSS/SSS的SINR值均有所下降.特别地,在UE数一定的情况下,随着小小区数目的增加,方案3中发送PSS/SSS的小小区数目也随着增加,从而造成其性能有所下降.在相同小小区数目情况下,方案3对应的SINR值明显高于方案2,进而说明方案3可有效抑制小小区间PSS/SSS的干扰.
|
图 5 小小区数目一定,UE接收PSS/SSS的SINR |
|
图 6 网络UE数一定,UE接收PSS/SSS的SINR |
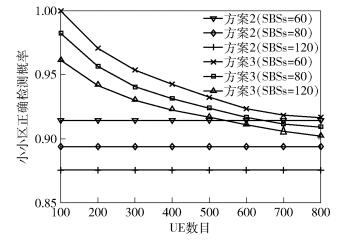
由图 7可知,相比于方案2,方案3能明显提高小小区的正确检测率,且在UE数较少的情况下,其优势更加明显.此外,方案3的小小区正确检测率随UE数目的增加而减小,反观方案2,其对应的小小区正确检测率与UE数目无关.因为在方案3中,随着UE数的增加,发送PSS/SSS的小小区也将随之增加,小小区间PSS/SSS的同频干扰强度变大,导致小小区的正确检测率下降.然而,在方案2中,由于每个小小区的PSS/SSS是连续发送,小小区间PSS/SSS的干扰与UE数目无关.
|
图 7 小小区正确检测率与UE数的关系 |
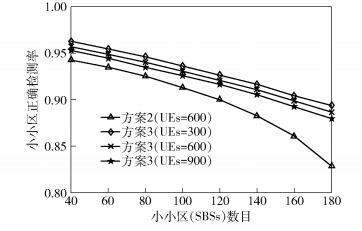
图 8表明,在不同UE数的情况下,方案3对应的小小区正确检测率均高于方案2.其原因在于,方案3有效地抑制了小小区间PSS/SSS干扰.特别地,在方案3中,发送PSS/SSS的SBSs数目会随着小小区数目的增加而增加,进而导致小小区间PSS/SSS干扰增大.从图 8亦可看出,在小小区数目较大的情况下,方案3较方案2优势更加明显.
|
图 8 小小区正确检测率与小小区数目的关系 |
为解决由小小区大量部署而带来的小小区间严重的PSS/SSS干扰与UE小小区发现能耗问题,提出一种基于TOA指纹数据库与PSS/SSS灵活传输的小小区发现方法.该方案利TOA位置信息来控制UE的IFS过程与SBSs的PSS/SSS发送,从而避免UE执行大量无效的IFS操作,同时降低同一时间段网络中发送PSS/SSS的SBSs数目,以达到UE节能与小小区间PSS/SSS干扰抑制的目的.仿真表明,所提方案较单纯的基于指纹数据库方案,不但能有效减少UE能耗,还能显著降低小小区之间的PSS/SSS干扰,提高小小区的正确检测率.
| [1] | Onireti O, Imran A, Imran M A, et al. On energy efficient inter-frequency small cell discovery in heterogeneous networks[C]//2015 IEEE International Conference on Communications (ICC). London: IEEE, 2015: 13-18. |
| [2] | Onireti O, Imran A, Imran M A, et al. Energy efficient inter-frequency small cell discovery in heterogeneous networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7122–7135. doi: 10.1109/TVT.2015.2482818 |
| [3] | Lopez V F, Pedersen K, Soret B, et al. Improving dense network performance through centralized scheduling and interference coordination[J]. IEEE Transactions on Vehicular Technology, 2016, 66(5): 4371–4382. |
| [4] | Hong Y T, Xu X D, Tao M L. Predictive connection time based small cell discovery strategy for LTE-advanced and beyond[C]//2014 Wireless Communications and Network-ing Conference (WCNC). Istanbul: IEEE, 2014: 2061-2066. |
| [5] | Prasad A, Lunden P, Tirkkonen O, et al. Energy efficient small-cell discovery using received signal strength based radio maps[C]//Vehicular Technology Conference (VTC Spring). Dresden: IEEE, 2013: 1-5. |
| [6] | Mahbas A. Double spectrum small cell (DSSC) for discovering inter-frequency small cell in HetNet[C]//2015 IEEE International Conference on Communications (ICC). London: IEEE, 2015: 3454-3459. |
| [7] | Peng S, Tong E, Jiang H, et al. An improved graph coloring based small cell discovery scheme in LTE hyper-dense networks[C]//Wireless Communications and Networking Conference Workshops (WCNCW). New Orleans: IEEE, 2015: 17-22. |
| [8] | Ji X, Zhang Y, Zhang Z, et al. An efficient synchronization signal design for neighboring cell search[C]//Vehicular Technology Conference. Seoul: IEEE, 2014: 1-5. |


