由于毫米波信号波长较短(1~10mm)，其具有较高的自由空间路径损耗^[1-2]，多径信道内散射簇有限，再加上信号的高频特性，导致其信道相干时间较小，使得毫米波信道的特性有别于传统蜂窝网络信号的信道特性，从而使现有的用户调度算法不能直接用于毫米波通信.因此，为了解决毫米波信道条件下有限区域内多用户调度问题，受传统多用户多输入多输出(MU-MIMO，multi-user multi-input multi-output)调度方案(随机波束成形方案(RBF, random beamforming)^[3]、基于破零预编码的半正交选择方案(SUS-ZFBF，the semi-orthogonal user selection with zero-forcing beamforming)^[4]等)的启发，提出了一种适用于该场景下的毫米波多用户多输入单输出(MU-MISO, multi-user multi-input single-output)自适应用户调度方案.不同于传统方案，提出了根据用户分布区域进行分组，并根据区域内用户密度为每个区域分配合适的射频链资源与通信波束的自适应调度方案.方案中，假设不同区域具有相近的区域面积，相互隔离，且每用户信道内均有一主簇多径(主要的通信多径)，此外同一区域内的用户具有相同主簇多径的发射角(AoD, angle of departure)分布区间.其次，在具体的用户选择过程中，根据匹配用户反馈的波束间信干噪比(SINR, signal to interference plus noise ratio)值，采用传统的空间聚类手段为每个预分配的离散傅里叶变换(DFT, discrete fourier transform)波束匹配到一个最佳用户.最后，针对区域内被选用户的数字信号，采用ZFBF预编码进行处理，以消除区域内用户间的干扰.在整个方案设计过程中，所需要的反馈信息包括用户接入基站时所处的区域位置信息以及波束匹配的用户计算得到的通信波束间的SINR值和具体的信道状态信息.

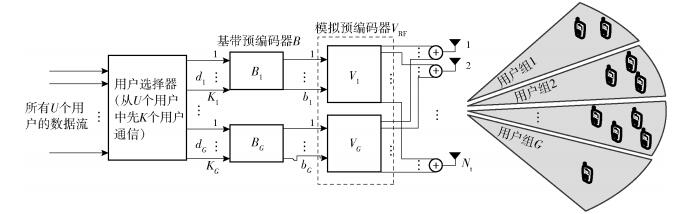
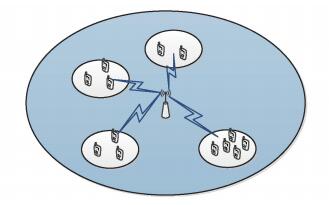
1 系统模型 1.1 信号模型

主要考虑毫米波MU-MISO下行链路系统，如图 1所示.现假设U个单天线用户随机分布在G个有限的固定区域内(见图 2)，每个区域随机分布了U_g个用户，即满足$ \sum\limits_{g = 1}^G {{U_g} = U} $，且基站端部署有N_t根发射天线，N_RF条射频链.假设基站从第g组区域U_g个用户中选取K_g个用户进行通信，且$\sum\limits_{g = 1}^G {{K_g} = K} $，即从U个用户中选出K个用户进行通信，且满足K≤N_RF≤N_t.在第g组用户群中，U_g个用户多径信道的主散射簇分布在同一角度范围内.

在下行链路中，基站端采用两段式多用户混合预编码设计方案^[5]，包括一个N_t×N_RF维的RF预编码器V=[V₁, V₂, …, V_G]和N_RF×K维的MU-MIMO块对角预编码矩阵B=diag(B₁, B₂, …, B_G)，其中${\mathit{\boldsymbol{V}}_g} \in {\mathbb{C}^{{N_{\rm{t}}} \times {b_g}}} $和对角元素$ {{\mathit{\boldsymbol{B}}}_{g}}\in {{\mathbb{C}}^{{{b}_{g}}\times {{K}_{g}}}}$分别表示基站对第g组被选用户的模拟和数字预编码矩阵，满足$ |{[{\mathit{\boldsymbol{V}}_g}]_{m.n}}| = 1/\sqrt {{N_{\rm{t}}}} $和$ \sum\limits_{g = 1}^G {{b_g} = {N_{{\rm{RF}}}}} $，且第g组区域分配的RF数b_g≥K_g. 此外系统的功率约束条件满足 $\parallel \mathit{\boldsymbol{VB}}\parallel _{\rm{F}}^2 = K $ ^[5-6].经系统调度后，第g组被选用户g_k的接收信号y_gk可表示为

$ \begin{array}{*{20}{c}} {{y_{{g_k}}} = {\mathit{\boldsymbol{h}}_{{g_k}}}\mathit{\boldsymbol{VBd}} + {\mathit{\boldsymbol{z}}_{{g_k}}} = }\\ {{\mathit{\boldsymbol{h}}_{{g_k}}}{\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{b}}_{{g_k}}}{d_{{g_k}}} + {\mathit{\boldsymbol{h}}_{{g_k}}}\sum\limits_{i = 1,i \ne k}^K {{\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{b}}_{{g_i}}}{d_{{g_i}}}} + }\\ {{\mathit{\boldsymbol{h}}_{{g_k}}}\sum\limits_{g' = 1,g' \ne g}^G {{\mathit{\boldsymbol{V}}_{g'}}{\mathit{\boldsymbol{b}}_{g'}}{d_{g'}} + {\mathit{\boldsymbol{z}}_{{g_k}}}} } \end{array} $

(1)

其中：d=[d₁, d₂, …, d_G]^T∈ $ {{\mathbb{C}}^{K}}$表示系统总的传输数据流矢量，d_g=[d_g1, d_g2, …, d_gKg]^T表示第g组被选用户的传输数据流矢量，且满足$E\{ \mathit{\boldsymbol{d}}{\mathit{\boldsymbol{d}}^{\rm{H}}}\} = \frac{P}{K}{\mathit{\boldsymbol{I}}_K} $，P表示平均的总传输功率值，即假设不同的用户数据流间具有相同的平均传输功率；h_gk∈ $ {{\mathbb{C}}^{1\times {{N}_{\text{t}}}}}$表示基站到第g组被选用户g_k的信道矢量；z_gk表示独立同分布且服从均值为0、方差为σ²的复高斯噪声，即z_gk~CN(0, σ²).此外，定义信噪比(SNR, signal to noise ratio)为ζ=P/σ²，则用户g_k的SINR可表示为

$ \varepsilon = \frac{{{{\left| {{\mathit{\boldsymbol{h}}_{{g_k}}}{\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{b}}_{{g_k}}}} \right|}^2}}}{{\frac{K}{\zeta } + \sum\limits_{i \ne k} {{{\left| {{\mathit{\boldsymbol{h}}_{{g_k}}}{\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{b}}_{{g_k}}}} \right|}^2}} + \sum\limits_{g' \ne g} {{{\left\| {{\mathit{\boldsymbol{h}}_{{g_k}}}{\mathit{\boldsymbol{V}}_{g'}}{\mathit{\boldsymbol{B}}_{g'}}} \right\|}^2}} }} $

(2)

1.2 信道模型

由于毫米波信号具有较高的路径损耗特性和毫米波信道有限的散射特性，现有研究^[5-6]均采用了几何信道模型对毫米波信道进行建模.因此，笔者也采用这种信道模型，并假设每个用户的信道内均具有N_cl个散射簇，且每个簇内均含有N_ray条传播路径.则基于此信道模型下，信道矩阵可表示为

$ \mathit{\boldsymbol{h}} = \gamma \sum\limits_{i = 1}^{{N_{{\rm{cl}}}}} {\sum\limits_{l = 1}^{{N_{{\rm{ray}}}}} {{\alpha _{i,l}}\mathit{\boldsymbol{a}}_t^{\rm{H}}\left( {{\theta _{i,l}}} \right)} } $

(3)

其中：α_{i, l}和$ {\theta _{i, l}} \in [{\theta _{i, {\rm{min}}}}, {\theta _{i, {\rm{max}}}}]$分别表示第i个散射簇内第l条多径信道的复增益值和AoD值，$[{\theta _{i, {\rm{min}}}}, {\theta _{i, {\rm{max}}}}] $则表示第i个散射簇AoD的角度扩散区间，且$ E\{ |{\alpha _{i, l}}{|^2}\} = \sigma _{i, \alpha }^2$；此外，γ是一个常数，且使约束条件E{‖h‖_F²}=N_t成立^[6]；最后，a_t(θ_{i, l})则表示了基站端的天线阵列响应矢量.为了便于后续的分析，考虑使用统一的线性天线阵列(ULA, uniform linear array)作为通信阵列，且天线阵元间间距为半波长，即D=λ/2，λ为信号波长，则ULA标准的阵列响应矢量a_t(θ)可表示为

$ {\mathit{\boldsymbol{a}}_{\rm{t}}}\left( \theta \right) = \frac{{{{\left[ {1,{{\rm{e}}^{{\rm{j \mathsf{ π} }}\sin \theta }}, \cdots ,{{\rm{e}}^{{\rm{j \mathsf{ π} }}\left( {{N_{\rm{t}}} - 1} \right)\sin \theta }}}\right]}^{\rm{T}}}}}{{\sqrt {{N_{\rm{t}}}} }} $

(4)

基于所考虑的场景进行建模时，为了更好地区别每个用户的主簇(主要的通信簇)与次簇空间，假设主簇的复增益变化功率值远大于其他所有次簇的复增益功率值，即满足$ \sigma _{i, \alpha }^2 \gg \sigma _{j, \alpha }^2(\forall j \in \{ 1, \ldots , i - 1, i + 1, \ldots , {N_{{\rm{cl}}}}\} )$.

2 多用户调度

受传统多用户MIMO调度方案的启发，提出了一种有限区域内基于预定义随机码本，且使得波束间干扰最小的自适应用户调度方案.假设通信过程中，基站已知每个区域的角度范围$ [{\theta _{g, {\rm{min}}}}, {\theta _{g, {\rm{max}}}}]$和用户已知基站广播的波束信息，并能根据信道估计技术^[7]获取到对应的信道状态信息h，则整个调度过程描述如下.

2.1 自适应分配射频资源及通信波束设计

假设用户与基站初次通信或当用户所在区域位置变化较大时，用户需要向基站发送接入请求信号，且接入信号中包含该用户大致的区域位置信息，而非具体的位置信息.

根据每个接入用户发送的位置信息，基站对所有用户进行区域归类和用户统计，并分别计算每个区域内的平均用户密度ρ_g=U_g/S_g，其中S_g表示第g组区域的区域面积.而后，基站根据每个区域的ρ_g值，为每个区域按以下规则分配合适的RF链资源：

$ \begin{array}{*{20}{c}} {{\rho _1}:{\rho _2}: \cdots :{\rho _G} = {b_1}:{b_2}: \cdots :{b_G}}\\ {{\rm{s}}.\;{\rm{t}}.\;\sum\limits_{g = 1}^G {{b_g}} = {N_{{\rm{RF}}}}}\\ {{b_g} \le {b_{g,\max }},\forall g} \end{array} $

(5)

其中b_{g, max}表示基站为第g组区域分配最多的射频链数.

为每个区域分配完射频链资源后，基站根据每个区域的角度范围[θ_{g, min}, θ_{g, max}]和分配的RF链数b_g(≠0)，通过式(4)为每个区域设计相应的通信波束，其过程为

$ \begin{array}{*{20}{c}} {{\theta _g} = \left\{ {{\theta _{g,\min }}:\left( {{\theta _{g,\max }} - {\theta _{g,\min }}} \right)/{b_g}:{\theta _{g,\max }}} \right\}}\\ {{\mathit{\boldsymbol{V}}_g} = \left\{ {{\mathit{\boldsymbol{a}}_{\rm{t}}}\left( \theta \right)\left| {\forall \theta \in {\theta _g}} \right.} \right\}}\\ {{\rm{s}}.\;{\rm{t}}.\;\left( {{\theta _{g,\max }} - {\theta _{g,\min }}} \right)/{b_g} \ge {\rm{ \mathsf{ π} }}/{N_{\rm{t}}}} \end{array} $

(6)

其中：π/N_t表示系统中模拟移相器设置的最小分辨率(波束宽度)，即基站为每个区域设计的波束宽度应大于等于最小波束宽度.从而可知，根据不同区域的用户密度，基站为每个区域设计通信波束的波束宽度(分辨率)有所差别，即用户密集区域采用细波束通信，而用户稀疏区域采用宽波束通信，并保证能够覆盖区域的角度范围.随之，基站将所设计的区域波束信息以广播信号的方式向所有接入用户进行广播，使得每个用户均能获知基站在某个时隙内的通信波束V=[V₁, V₂, …, V_G].

2.2 基于传统的空间聚类手段选择用户

在现有多用户调度算法^[8]的启发下，采用传统的空间聚类方法进行用户选择，并将整个用户选择过程分为2步.

首先，在用户端，每个用户根据已知的信息，通过波束双锥匹配模型^[8-9]为其匹配满足匹配约束条件α(0≤α≤1)的波束，不同于文献[8]中在基于低频信道二阶统计特性的情况下，以最大化信道幅度和信号的准SINR值作为每个用户选择匹配波束的准则，笔者则是将最小化波束间干扰情况同时作为用户和波束双向匹配过程的判决条件.即有

$ {\mathit{\Gamma }_{{g_k}}} = \left\{ {i\left| {\frac{{\left| {{\mathit{\boldsymbol{h}}_{gk}}{\mathit{\boldsymbol{v}}_i}} \right|}}{{\left\| {{\mathit{\boldsymbol{h}}_{gk}}} \right\|}} \ge \alpha ,{\mathit{\boldsymbol{v}}_i} \subset \mathit{\boldsymbol{V}},i = 1,2, \cdots ,{N_{{\rm{RF}}}}} \right.} \right\} $

(7)

其中Γ_gk和h_gk分别表示第g组第k个用户的匹配通信波束编号集和信道矩阵.

当用户g_k匹配的通信波束编号集Γ_gk为非空集时，区别于文献[8]以最大信道幅度作为用户匹配波束的标准，在只考虑通信波束间干扰的情况下，提出通过其余所有通信波束对某一匹配波束的干扰情况来判决用户g_k的最佳通信波束，以保证用户g_k能够获取到使得波束间干扰达到最小的波束i^*_gk∈Γ_gk，即有

$ \begin{array}{*{20}{c}} {i_{{g_k}}^ * = \mathop {{\mathop{\rm argmax}\nolimits} }\limits_{i \in {\mathit{\Gamma }_{{g_k}}}} R\left( {{g_k}} \right) = }\\ {\mathop {{\mathop{\rm argmax}\nolimits} }\limits_{i \in {\mathit{\Gamma }_{{g_k}}}} \frac{{{{\left| {{\mathit{\boldsymbol{h}}_{gk}}{\mathit{\boldsymbol{v}}_i}} \right|}^2}}}{{1 + \sum\limits_{{\mathit{\boldsymbol{v}}_j} \subset \mathit{\boldsymbol{V}},{\mathit{\boldsymbol{v}}_j} \ne {\mathit{\boldsymbol{v}}_i}} {{{\left| {{\mathit{\boldsymbol{h}}_{gk}}{\mathit{\boldsymbol{v}}_j}} \right|}^2}} }}} \end{array} $

(8)

用户g_k将所得信道质量标识信息(CQI，channel quality indicator)以及对应的信道状态信息CSI反馈回基站，其中CQI包括最佳波束编号i^*_gk和对应的R(g_k)_max.不同于文献[8]，其反馈的R(g_k)_max值是用户信号的准SINR值，仅用于基站端的波束匹配用户过程，而所计算的R(g_k)_max值表示的是波束间的干扰情况，并分别应用于用户端和基站端的用户-波束对的双向匹配过程.若Γ_gk= $ \emptyset $，用户g_k则不需要反馈任何信息.

其次，在基站端，基站根据获得的反馈信息为每个通信波束最终确定匹配的用户，使之与基站通信，即有

$ {k_{g,i}} = \mathop {{\mathop{\rm argmax}\nolimits} }\limits_{k \in {\mathit{W}_{g,i}}} R\left( {{g_k}} \right) $

(9)

直到选出K个用户或者W_{g, i}=$ \emptyset $为止.其中，W_{g, i}表示基站端得到的第g组第i(1≤i≤b_g)个预定义波束对应的反馈用户集.

2.3 基于ZFBF的数字预编码

经调度后，采用ZFBF预编码方法对组内被选用户信号进行数字处理，即定义$ {{\mathit{\boldsymbol{\bar h}}}_{{g_k}}} = {\mathit{\boldsymbol{h}}_{{g_k}}}{\mathit{\boldsymbol{V}}_g}$表示第g组内被选用户g_k等效的信道矢量，则第g组用户MU-MIMO预编码矩阵${\mathit{\boldsymbol{B}}_g} = \mathit{\boldsymbol{\bar H}}_g^{\rm{H}}{({{\mathit{\boldsymbol{\bar H}}}_g}\mathit{\boldsymbol{\bar H}}_g^{\rm{H}})^{ - 1}} $，其中${{\mathit{\boldsymbol{\bar H}}}_g} = {[\mathit{\boldsymbol{h}}_{{g_1}}^{\rm{H}}, \mathit{\boldsymbol{h}}_{{g_2}}^{\rm{H}}, \ldots , \mathit{\boldsymbol{h}}_{{g_{{K_g}}}}^{\rm{H}}]^{\rm{H}}} $表示第g组所有被选用户等效信道矢量的联合矩阵.又已知系统需要满足约束条件‖VB‖_F²=K，且${\mathit{\boldsymbol{B}}_g} = [{\mathit{\boldsymbol{b}}_{{g_1}}}, {\mathit{\boldsymbol{b}}_{{g_2}}}, \ldots , {\mathit{\boldsymbol{b}}_{{g_{{K_g}}}}}] $, 则归一化表示为$ {\mathit{\boldsymbol{b}}_{{g_k}}} = {\mathit{\boldsymbol{b}}_{{g_k}}}/\parallel {\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{b}}_{{g_k}}}{\parallel _{\rm{F}}}, k = 1, 2, \ldots , {K_g}$.

3 仿真结果

下面主要讨论所提用户调度方案在不同条件下的仿真结果.假设基站端部署有N_t=64根发射天线的ULA，N_RF=16条射频链，噪声功率σ_gk²=σ²=1($\forall $ g_k).为了便于分析，假设系统中用户随机集中分布在G=4组固定的通信区域内，且各区域角度区间分布分别为[-170°, -150°]、[-70°, -50°]、[10°, 30°]和[110°, 130°].此外，用户多径信道散射簇数N_cl=4，各散射簇内多径数均为N_ray=6，且主散射簇复增益变化功率(CGPMSC, complex gain power of main scattering cluster)为σ_{i, α}²，次散射簇$\sigma _{j, \alpha }^2 = 1(\forall j \in \{ 1, \ldots , i - 1, i + 1, \ldots , {N_\rm{cl}}\} ) $，则信道矩阵常数$ \gamma = \sqrt {{N_{\rm{t}}}/({N_{{\rm{ray}}}}({N_{{\rm{cl}}}} - 1 + \sigma _{i, \alpha }^2))} $.

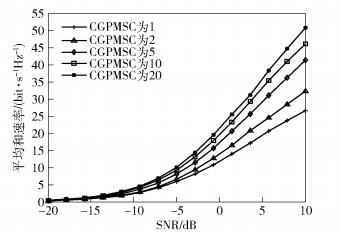
为了验证所提算法在所定义的通信场景下具有鲁棒性，对用户多径信道内不同的主簇复增益功率(分别为1、2、5、10、20)下和速率性能随SNR变化的曲线进行了仿真，如图 3所示，其中匹配约束条件α=0.1.可知，当SNR值一定时，随功率值σ_{i, α}²的增大，系统的和速率也随之增大，且当σ_{i, α}²=1时，即问题退化到当用户多径信道内通信簇之间不存在主次之分时，系统获得的和速率性能最低.从而可证，在有限区域的通信场景内，当$\sigma _{i, \alpha }^2 \gg \sigma _{j, \alpha }^2 $时，所提算法具有一定的鲁棒性.

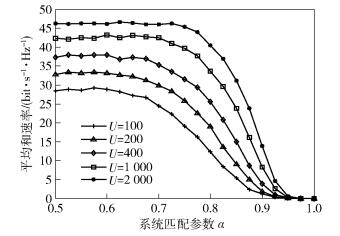
所提算法获得的系统和速率性能随匹配约束条件α的变化趋势如图 4所示，其中$ \sigma _{i, \alpha }^2$ =10，SNR为5dB，U={100, 200, 400, 1000, 2000}.由图可知，在用户数U一定的条件下，在一定范围内系统和速率基本不变，但是当其大于某个值时，和速率性能随α值的增大而急剧下降，该拐点的值称为最大的最佳匹配参数α_{opt, max}.另外，α_{opt, max}随用户数U的增大而增大，这是由于用户数U越大，区域内用户密度越大，每个预定义波束匹配到满足约束条件的用户概率越大.且α表示用户信道矢量方向与预定义波束矢量方向的夹角余弦值，α越大，夹角越小，即表示两矢量间的匹配程度越高，但相应地区域内满足条件的用户数会大幅度减小，甚至为0.因此，当α∈(0, α_{opt, max}]时，系统依然能匹配到既满足匹配约束条件，又能使波束间干扰最小的用户，从而不改变系统的和速率性能.而当α∈(α_{opt, max}, 1]时，匹配程度变高，导致部分预定义的随机波束未能匹配到用户，进而导致系统和速率值下降.

此外，为了验证所提算法使用宽窄不一的通信波束与多用户进行通信，能够获得比使用固定波束码本通信获得的和速率性能更高，即所提算法性能更优.对所提算法在DFT码本^[10]下的性能也进行了仿真，仿真结果如图 5所示.其中U=400，σ_{i, α}²=10.相比于DFT码本，系统采用提出的基于用户密度设计的通信波束进行通信时，所获得的和速率更高，且两者间和速率差距随SNR的增大而变大.这是由于基站为每个区域分配的射频链资源有限，且无法获知每个用户具体的位置信息，所以当使用DFT码本进行通信时，基站是根据区域的射频链数从覆盖该区域的DFT波束码本子集中随机选取相应的波束数对该区域进行通信的.因此，系统无法保证所选的DFT通信波束能够覆盖到区域内的所有用户，且均能匹配到对应最佳的通信用户，即存在通信波束零匹配用户的问题，从而导致系统性能的大幅度下降.

此外，将所提的算法和SUS-ZFBF算法进行了性能对比，但由于SUS-ZFBF算法不能直接应用于毫米波通信场景下，笔者对该算法进行了调整，让其中被选用户的通信波束使用DFT码本^[10]，并采用ZFBF预编码方式处理区域内被选用户的等效数字信号，其阈值参数β=0.4，N_t=64，其余参数及系统结构与所提算法基本一致.与SUS-ZFBF算法相比，所提算法获得的和速率性能具有一定差距，但仍获得了较好的和速率.这是因为SUS-ZFBF算法在获取到所有通信用户具体的CSI条件下，利用用户信道的近似正交特性选择服务用户，并通过DFT波束码本为每个被选用户匹配最佳的通信波束，从而减小了被选用户间的干扰，提升了系统和速率性能.但由于SUS-ZFBF算法需要获取到所有用户具体的CSI，而所提方案只需要知道部分匹配用户的CSI，而且所提方案所需的部分反馈信息从数学角度上看，比如用户所处的区域位置信息和波束间的SINR值，这些均是一些具体的数值标量，相对于矩阵形式CSI，其所需要的反馈量也较小.因此所提方案降低了系统反馈开销，提升了系统处理效率.

4 结束语

提出了一种基于部分匹配用户的CQI信息及毫米波MU-MISO下行链路信道下的自适应用户调度方案，适用于用户移动性低且集中分布在有限区域内的场景中，比如用户成群分布的露天宽旷区域等.相比于固定码本通信，笔者根据不同区域的用户密度，设计了不同宽度的波束与区域内用户进行通信，即用户稀疏区域采用宽波束通信，而用户密集区域采用窄波束通信，这不仅保证了分配的波束能覆盖全区域内的用户，并能匹配到满足条件下的用户，还能够解决采用固定波束通信导致的性能大幅度下降问题和射频资源分配的不公平性问题.此外，与SUS-ZFBF相比，所提算法在使用波束双锥匹配模型筛选用户的基础上，选择既满足约束条件又使得波束间干扰最小的用户作为通信用户，进一步减少了反馈信息量，提升了系统处理效率.