2. 北京航空航天大学 经济管理学院, 北京 100191
提出了一种基于云制造平台的供应链生产计划方法.构建了以最大完工时间、总服务成本和总运输成本为优化目标的供应链生产计划模型,设计了遗传算法和改进遗传退火算法,对模型进行求解,建立了基于最大完工时间和总成本的算法选择模型.利用仿真算例比较了2种算法在不同情况下的求解效果,并给出了算法的选择准则.仿真结果表明,该方法能为以云制造平台为调度主体的供应链制定合理的生产计划.
2. School of Economics and Management, Beihang University, Beijing 100191, China
A production planning method of supply chain based on cloud manufacturing platform was presented. The purposes of this method were to minimize the makespan, total service cost and total transportation cost. In order to effectively solve the presented model, a genetic algorithm and an improved genetic-annealing algorithm were designed. Meanwhile, a model for selecting the efficient algorithms was established based on the makespan and total cost. The results of two algorithms in different situations were compared by simulation example, and then a selection criteria of the algorithms was given. The simulation results shown that the proposed method can provide a reasonable production plan for the supply chain based on the cloud manufacturing platform.
云制造环境下的云资源需求者与提供者分布在供应链的不同环节,使为基于云制造平台的供应链制定生产计划较为困难.因此,研究以云制造平台为核心的供应链生产计划方法具有非常重要的意义.肖莹莹等[1]为面向云制造用户多品种定制的分布式供应链设计了多目标生产运输优化调度模型.熊永华等[2]为云环境的虚拟资源调度问题构建了多目标优化模型. Pérez-Lechuga等[3]为日用消费品市场设计了短期生产计划模型,用于建立供应链与生产计划的联系. Hassanzadeh[4]构建了基于0~1整数规划法的云制造供应商选择模型和基于线性规划法的项目计划模型. Liu等[5]研究了云制造环境中的基于工作量的多任务调度问题,但未对以云制造平台为调度主体供应链的生产计划方法展开深入研究.基于此,提出一种基于云制造平台的供应链生产计划方法,包括为以云制造平台为调度主体的供应链构建生产计划模型、设计启发式算法、构建算法选择模型等,主要用于解决以云制造平台为调度主体的供应链生产计划问题.
1 云制造平台的供应链生产计划模型 1.1 问题描述云制造平台为供应链中需求云资源的一系列分布式任务中的子任务分配合适的云资源提供商,并确定各子任务接受服务的时间,使得由该云制造平台主导的供应链目标函数达到最优.
1.2 假设条件假设条件主要包括:1)无并行子任务;2)同一任务中的各子任务存在先后约束关系;3)实体中间件在前后云资源提供商之间转运时需要考虑运输时间和成本,且运输时间可纳入前一个子任务的服务时间中.
1.3 模型构建1) 最大完工时间
| $ \min {f_{{\rm{at}}}} = \max \left( {{E_{pnk}}} \right) $ | (1) |
其中:fat为最大完工时间,Epnk是任务k的第n个子任务(Tnk)接受云资源提供商p服务的结束时间.
2) 总服务成本
| $ \min {f_{{\rm{sc}}}} = \sum\limits_{p = 1}^P {\sum\limits_{k = 1}^K {\sum\limits_{n = 1}^{{n_k}} {S_{pnk}^c{x_{pnk}}} } } $ | (2) |
其中:fsc为总服务成本,Spnkc为云资源提供商p完成Tnk的成本;xpnk为0~1决策变量,当云资源提供商p完成了Tnk,xpnk=1,否则,xpnk=0;P为云资源提供商的数量;K为需求云资源的任务数量;nk为任务k的子任务数量.
3) 总运输成本
| $ \min {f_{{\rm{tc}}}} = \sum\limits_{p = 1}^P {\sum\limits_{q = 1}^P {\sum\limits_{k = 1}^K {\sum\limits_n^{{n_k} - 1} {T_{pq}^c{D_{pq}}{y_{pqkn\left( {n + 1} \right)}}} } } } $ | (3) |
其中:ftc为总运输成本;Tpqc为云资源提供商p到云资源提供商q单位距离的运输成本;Dpq为云资源提供商p到云资源提供商q的距离;ypqkn(n+1)为0~1决策变量,当Tnk的资源提供商p与T(n+1)k的资源提供商q之间存在实体中间件的运输时,ypqkn(n+1)=1,否则,ypqkn(n+1)=0.
约束条件主要包括
| $ \sum\limits_{k = 1}^K {\sum\limits_{n = 1}^{{n_k}} {{x_{pnk}} \le 1} } $ | (4) |
| $ \sum\limits_{p = 1}^P {{x_{pnk}} \le 1} $ | (5) |
| $ {S_{pk1}} = 0 $ | (6) |
| $ {E_{pnk}} = {S_{pnk}}{x_{pnk}} + S_{pnk}^t{x_{pnk}} + T_{pq}^t{D_{pq}}{y_{pqkn\left( {n + 1} \right)}} $ | (7) |
| $ {S_{pnk}} \ge {E_{q\left( {n - 1} \right)k}} $ | (8) |
| $ {S_{pnk}} \ge {E_{pij}} $ | (9) |
其中:Spnk为Tnk接受云资源提供商p服务的开始时间,Spnkt为云资源提供商p完成Tnk所需的时间,Tpqt为资源提供商p到云资源提供商q单位距离的运输时间.
式(4)表示云资源提供商p在某时刻最多为一个子任务服务.式(5)表示Tnk在某时刻最多占用一种云资源.式(6)表示若由云资源提供商p服务的T1k没有紧前任务,则T1k在0时刻开始被服务.式(7)表示Tnk被服务的结束时间等于其被服务的开始时间+云资源提供商p的服务时间+由云资源提供商p运往相连接的云资源提供商q的运输时间.式(8)表示Tnk被服务的开始时间≥T(n-1)k被服务的结束时间.式(9)表示当Tij是Tnk在云资源提供商p处的紧前任务时,Tnk接受云资源提供商p服务的开始时间≥Tij接受云资源提供商p服务的结束时间.
2 算法设计 2.1 遗传算法设计1) 编码设计
采用双层编码方式:第1层是子任务编码;第2层是为第1层子任务提供服务的云资源提供商编码.
2) 适应度函数设计
利用极差变换法对fac与fat进行标准化处理,得到
| $ f = \frac{1}{{{w_1}{{\bar f}_{{\rm{at}}}} + {w_2}{{\bar f}_{{\rm{ac}}}}}} $ | (10) |
其中:fac=fsc+ftc,0≤w1, w2≤1,且w1+w2=1.
3) 交叉操作
① 按轮盘赌法从原种群中选出2个染色体,取其第1层基因,利用单点交叉方式对子任务进行交叉操作;②利用原染色体中子任务与云资源提供商的匹配关系,将相应的云资源提供商分配给交叉后的子任务,得到交叉后的新染色体.
4) 变异操作
① 按“随机选择”的方式从种群中选择待变异的染色体;②从待变异染色体第1层子任务的可选云资源提供商元胞矩阵中随机选取新云资源提供商,分配给相应的子任务,得到变异后的新染色体.
2.2 改进遗传退火算法设计1) 模拟退火算法的引入
在交叉、变异后对种群进行更新时,按照Metropolis准则以P=e-df/T的概率接受恶化解.当遗传操作完成一代进化时,判断代数是否达到最大遗传代数;若未达到,则按指定的退火系数对当前温度降温,进而判断是否达到终止温度;若未达到则继续循环进化寻优;否则,退出迭代过程,输出最优解.
2) 变异操作的改进
将“随机选择”的变异操作方式改进为“服务时间和成本按指定权重比的加权和更小的云资源提供商被选择的概率更大”的变异操作方式.
3 算法选择模型构建在算法选择时,考虑的决策目标包括fat和fac.
| $ {f_{1\left( {{w_1},{w_2}} \right)}}\left( A \right) = {f_{{\rm{at}}\left( {{w_1},{w_2}} \right)}}\left( A \right) $ | (11) |
| $ {f_{2\left( {{w_1},{w_2}} \right)}}\left( A \right) = {f_{{\rm{ac}}\left( {{w_1},{w_2}} \right)}}\left( A \right) $ | (12) |
可利用式(13)对fat和fac进行标准化处理.
| $ {R_{l\left( {{w_1},{w_2}} \right)}}\left( {{A_r}} \right) = \frac{{{f_{l\left( {{w_1},{w_2}} \right)}}\left( {{A_r}} \right)}}{{\sum\limits_{r = 1}^2 {{f_{l\left( {{w_1},{w_2}} \right)}}\left( {{A_r}} \right)} }} $ | (13) |
将2个决策目标进行线性加权,得到
| $ {f_{\left( {{w_1},{w_2}} \right)}}\left( A \right) = \alpha {R_{1\left( {{w_1},{w_2}} \right)}}\left( A \right) + \left( {1 - \alpha } \right){R_{2\left( {{w_1},{w_2}} \right)}}\left( A \right) $ | (14) |
其中:A={Ar|r=1, 2},r为算法编号,当r=1时,Ar为遗传算法;当r=2时,Ar为改进遗传退火算法;Rl(w1, w2)为经过标准化处理的数据,l为决策目标编号,即在w1和w2取定一组值的情况下,当l=1时,Rl(w1, w2)为fat的标准化数据;当l=2时,Rl(w1, w2)为fac的标准化数据;且α∈[0, 1].
4 算例设计及仿真结果分析 4.1 算例设计有8个需求云资源的分布式任务,每个任务可分为5个子任务,分别由10个云资源提供商提供服务.
任务可选云资源提供商元胞矩阵为M1. M1中的数组元素m1(i, j)由能够为第i个任务中的第j个子任务提供服务的云资源提供商的编号构成.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1} = }\\ {\left[ {\begin{array}{*{20}{c}} {\left\{ {3,6} \right\}}&{\left\{ 7 \right\}}&{\left\{ {10} \right\}}&{\left\{ {1,5,8} \right\}}&{\left\{ 4 \right\}}\\ {\left\{ 4 \right\}}&{\left\{ {2,10} \right\}}&{\left\{ {5,6} \right\}}&{\left\{ 8 \right\}}&{\left\{ {7,8} \right\}}\\ {\left\{ {2,9} \right\}}&{\left\{ 5 \right\}}&{\left\{ {3,7} \right\}}&{\left\{ {10} \right\}}&{\left\{ 9 \right\}}\\ {\left\{ {5,6,7} \right\}}&{\left\{ 3 \right\}}&{\left\{ {2,9} \right\}}&{\left\{ 4 \right\}}&{\left\{ 6 \right\}}\\ {\left\{ {10} \right\}}&{\left\{ {1,4} \right\}}&{\left\{ 5 \right\}}&{\left\{ {2,7,8} \right\}}&{\left\{ {2,6} \right\}}\\ {\left\{ {3,4,10} \right\}}&{\left\{ 9 \right\}}&{\left\{ 1 \right\}}&{\left\{ 2 \right\}}&{\left\{ {3,4} \right\}}\\ {\left\{ 6 \right\}}&{\left\{ {10} \right\}}&{\left\{ {4,8} \right\}}&{\left\{ {5,6} \right\}}&{\left\{ {1,5} \right\}}\\ {\left\{ 7 \right\}}&{\left\{ {1,3,8} \right\}}&{\left\{ 9 \right\}}&{\left\{ {4,7} \right\}}&{\left\{ 5 \right\}} \end{array}} \right]} \end{array} $ |
服务时间元胞矩阵为M2 (单位:h). M2中的数组元素m2(i, j)是由能够为第i个任务中第j个子任务提供服务的云资源提供商服务的时间构成.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_2} = }\\ {\left[ {\begin{array}{*{20}{c}} {\left\{ {6,2} \right\}}&{\left\{ 4 \right\}}&{\left\{ 5 \right\}}&{\left\{ {4,3,10} \right\}}&{\left\{ 2 \right\}}\\ {\left\{ 3 \right\}}&{\left\{ {2,5} \right\}}&{\left\{ {8,3} \right\}}&{\left\{ 5 \right\}}&{\left\{ {2,2} \right\}}\\ {\left\{ {2,5} \right\}}&{\left\{ 3 \right\}}&{\left\{ {4,4} \right\}}&{\left\{ 3 \right\}}&{\left\{ 6 \right\}}\\ {\left\{ {5,10,5} \right\}}&{\left\{ 3 \right\}}&{\left\{ {6,4} \right\}}&{\left\{ 6 \right\}}&{\left\{ 2 \right\}}\\ {\left\{ 4 \right\}}&{\left\{ {6,5} \right\}}&{\left\{ 3 \right\}}&{\left\{ {2,3,2} \right\}}&{\left\{ {5,3} \right\}}\\ {\left\{ {3,4,4} \right\}}&{\left\{ 5 \right\}}&{\left\{ 1 \right\}}&{\left\{ 3 \right\}}&{\left\{ {2,5} \right\}}\\ {\left\{ 5 \right\}}&{\left\{ 3 \right\}}&{\left\{ {8,4} \right\}}&{\left\{ {3,6} \right\}}&{\left\{ {5,5} \right\}}\\ {\left\{ 3 \right\}}&{\left\{ {4,3,4} \right\}}&{\left\{ 4 \right\}}&{\left\{ {3,3} \right\}}&{\left\{ 5 \right\}} \end{array}} \right]} \end{array} $ |
服务成本元胞矩阵为M3 (单位:元). M3中的数组元素m3(i, j)由能够为第i个任务中第j个子任务提供服务的云资源提供商服务的成本构成.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_3} = }\\ {\left[ {\begin{array}{*{20}{c}} {\left\{ {100,150} \right\}}&{\left\{ {50} \right\}}&{\left\{ {20} \right\}}&{\left\{ {80,100,65} \right\}}&{\left\{ {50} \right\}}\\ {\left\{ {30} \right\}}&{\left\{ {30,50} \right\}}&{\left\{ {60,40} \right\}}&{\left\{ {50} \right\}}&{\left\{ {50,80} \right\}}\\ {\left\{ {150,100} \right\}}&{\left\{ {55} \right\}}&{\left\{ {40,45} \right\}}&{\left\{ {70} \right\}}&{\left\{ {60} \right\}}\\ {\left\{ {60,20,55} \right\}}&{\left\{ {30} \right\}}&{\left\{ {120,160} \right\}}&{\left\{ {20} \right\}}&{\left\{ {40} \right\}}\\ {\left\{ {40} \right\}}&{\left\{ {60,90} \right\}}&{\left\{ {30} \right\}}&{\left\{ {100,60,80} \right\}}&{\left\{ {30,30} \right\}}\\ {\left\{ {100,70,70} \right\}}&{\left\{ {30} \right\}}&{\left\{ {45} \right\}}&{\left\{ {30} \right\}}&{\left\{ {100,45} \right\}}\\ {\left\{ {45} \right\}}&{\left\{ {30} \right\}}&{\left\{ {30,50} \right\}}&{\left\{ {40,20} \right\}}&{\left\{ {45,40} \right\}}\\ {\left\{ {35} \right\}}&{\left\{ {80,40,75} \right\}}&{\left\{ {40} \right\}}&{\left\{ {25,30} \right\}}&{\left\{ {50} \right\}} \end{array}} \right]} \end{array} $ |
运输作业矩阵为M4. M4中的元素m4(i, j)取0或1;若m4(i, j)=1,表示第i个任务中的第j个子任务需要运输,若m4(i, j)=0,表示第i个任务中的第j个子任务不需要运输.
| $ {\mathit{\boldsymbol{M}}_4} = \left[ {\begin{array}{*{20}{c}} 1&1&1&1&1\\ 0&0&0&1&1\\ 0&0&1&1&1\\ 0&1&1&1&1\\ 1&1&1&1&1\\ 0&1&1&1&1\\ 0&0&0&0&0\\ 0&0&0&0&1 \end{array}} \right] $ |
云资源提供商之间的距离矩阵为M5(单位:km). M5中的元素m5(i, j)表示云资源提供商i与云资源提供商j之间的距离. M5为对称矩阵.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_5} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&{70}&{50}&{50}&{30}&{30}&{70}&{30}&{70}&{60}\\ {}&0&{60}&{100}&{80}&{20}&{90}&{40}&{20}&{100}\\ {}&{}&0&{50}&{30}&{30}&{100}&{60}&{80}&{20}\\ {}&{}&{}&0&{10}&{60}&{10}&{70}&{60}&{50}\\ {}&{}&{}&{}&0&{30}&{70}&{90}&{80}&{60}\\ {}&{}&{}&{}&{}&0&{80}&{70}&{80}&{10}\\ {}&{}&{}&{}&{}&{}&0&{80}&{50}&{50}\\ {}&{}&{}&{}&{}&{}&{}&0&{100}&{40}\\ {}&{}&{}&{}&{}&{}&{}&{}&0&{80}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&0 \end{array}} \right]} \end{array} $ |
运输速度矩阵为M6(单位:km/h). M6中的元素m6(i, j)表示云资源提供商i与云资源提供商j之间进行实体中间件运输时的运输速度. M6为对称矩阵.当云资源提供商之间无运输距离时,对应的速度为无穷大,以Inf表示.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_6} = }\\ {\left[ {\begin{array}{*{20}{c}} {{\rm{Inf}}}&{75}&{92}&{89}&{95}&{98}&{58}&{58}&{82}&{50}\\ {}&{{\rm{Inf}}}&{95}&{85}&{99}&{82}&{67}&{85}&{71}&{98}\\ {}&{}&{{\rm{Inf}}}&{79}&{70}&{86}&{85}&{91}&{50}&{98}\\ {}&{}&{}&{{\rm{Inf}}}&{87}&{85}&{71}&{50}&{76}&{67}\\ {}&{}&{}&{}&{{\rm{Inf}}}&{84}&{63}&{65}&{52}&{56}\\ {}&{}&{}&{}&{}&{{\rm{Inf}}}&{71}&{83}&{90}&{66}\\ {}&{}&{}&{}&{}&{}&{{\rm{Inf}}}&{100}&{70}&{92}\\ {}&{}&{}&{}&{}&{}&{}&{{\rm{Inf}}}&{63}&{56}\\ {}&{}&{}&{}&{}&{}&{}&{}&{{\rm{Inf}}}&{72}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{{\rm{Inf}}} \end{array}} \right]} \end{array} $ |
单位运输成本矩阵为M7(单位:元). M7中的元素m7(i, j)表示云资源提供商i与云资源提供商j之间进行实体中间件运输时的单位运输成本. M7为对称矩阵.
| $ {\mathit{\boldsymbol{M}}_7} = \left[ {\begin{array}{*{20}{c}} 0&{1.5}&{1.8}&{1.5}&{1.8}&{1.8}&{1.3}&{1.3}&{1.5}&1\\ {}&0&{1.8}&{1.5}&{1.8}&{1.5}&{1.3}&{1.5}&{1.5}&{1.8}\\ {}&{}&0&{1.5}&{1.3}&{1.5}&{1.5}&{1.8}&1&{1.8}\\ {}&{}&{}&0&{1.5}&{1.5}&{1.5}&1&{1.5}&{1.3}\\ {}&{}&{}&{}&0&{1.5}&{1.3}&{1.3}&{1.3}&{1.3}\\ {}&{}&{}&{}&{}&0&{1.5}&{1.5}&{1.5}&{1.3}\\ {}&{}&{}&{}&{}&{}&0&{1.8}&{1.3}&{1.8}\\ {}&{}&{}&{}&{}&{}&{}&0&{1.3}&{1.3}\\ {}&{}&{}&{}&{}&{}&{}&{}&0&{1.5}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&0 \end{array}} \right] $ |
需求云资源的任务i与云资源提供商j之间的距离矩阵为M8. M8中的元素m8(i, j)表示需求云资源的任务i与云资源提供商j之间的距离.
| $ {\mathit{\boldsymbol{M}}_8} = \left[ {\begin{array}{*{20}{c}} {70}&{90}&{100}&{10}&{70}&{100}&{40}&{50}&{50}&{60}\\ {90}&{10}&{40}&{20}&{80}&{80}&{50}&{70}&{40}&{30}\\ {40}&{10}&{70}&{20}&{50}&{30}&{100}&{30}&{30}&{80}\\ {40}&{30}&{50}&{10}&{20}&{100}&{90}&{60}&{10}&{30}\\ {100}&{10}&{50}&{60}&{20}&{90}&{30}&{70}&{70}&{90}\\ {80}&{50}&{70}&{30}&{20}&{10}&{20}&{100}&{70}&{40}\\ {70}&{80}&{20}&{100}&{50}&{100}&{90}&{50}&{10}&{20}\\ {30}&{20}&{10}&{100}&{30}&{80}&{10}&{100}&{90}&{20} \end{array}} \right] $ |
运输速度矩阵为M9(单位:km/h). M9中的元素m9(i, j)表示需求云资源的任务i与云资源提供商j之间进行实体中间件运输时的运输速度.
| $ {\mathit{\boldsymbol{M}}_9} = \left[ {\begin{array}{*{20}{c}} {87}&{51}&{73}&{100}&{56}&{53}&{87}&{75}&{76}&{92}\\ {89}&{96}&{54}&{94}&{76}&{96}&{76}&{54}&{94}&{82}\\ {96}&{68}&{98}&{77}&{65}&{73}&{65}&{64}&{98}&{61}\\ {81}&{70}&{53}&{50}&{100}&{83}&{73}&{97}&{81}&{55}\\ {66}&{91}&{61}&{86}&{62}&{80}&{88}&{100}&{75}&{95}\\ {72}&{67}&{75}&{66}&{93}&{98}&{100}&{54}&{64}&{98}\\ {50}&{62}&{85}&{70}&{88}&{54}&{72}&{66}&{90}&{97}\\ {75}&{58}&{56}&{60}&{84}&{82}&{94}&{70}&{95}&{57} \end{array}} \right] $ |
单位运输成本矩阵为M10 (单位:元/km). M10中的元素m10(i, j)表示需求云资源的任务i与云资源提供商j之间进行实体中间件运输时的单位运输成本.
| $ {\mathit{\boldsymbol{M}}_{10}} = \left[ {\begin{array}{*{20}{c}} {1.5}&{1.3}&{1.5}&{1.8}&{1.3}&{1.3}&{1.5}&{1.5}&{1.5}&{1.8}\\ {1.5}&{1.5}&{1.3}&{1.8}&{1.5}&{1.8}&{1.5}&{1.3}&{1.8}&{1.5}\\ {1.8}&{1.3}&{1.8}&{1.5}&{1.3}&{1.5}&{1.3}&{1.3}&{1.8}&{1.3}\\ {1.5}&{1.3}&{1.3}&1&{1.8}&{1.5}&{1.5}&{1.8}&{1.5}&{1.3}\\ {1.3}&{1.8}&{1.3}&{1.5}&{1.3}&{1.5}&{1.5}&{1.8}&{1.5}&{1.8}\\ {1.5}&{1.3}&{1.5}&{1.3}&{1.8}&{1.8}&{1.8}&{1.3}&{1.3}&{1.8}\\ 1&{1.3}&{1.5}&{1.3}&{1.5}&{1.3}&{1.5}&{1.3}&{1.5}&{1.8}\\ {1.5}&{1.3}&{1.3}&{1.3}&{1.5}&{1.5}&{1.8}&{1.3}&{1.8}&{1.3} \end{array}} \right] $ |
设置的相关参数如下:群体大小Ps=50、最大遗传代数gmax=200、交叉概率Pc=0.8、变异概率Pm=0.2、初始温度T0=100、冷却系数k=0.95、终止温度Tend=0.05.
1) 2种算法求解结果对比
表 1所示为2种算法在每组w1和w2权重组合下分别运行10次得到结果的平均值.
|
|
表 1 2种算法分别运行10次所得结果的平均值 |
2) 算法选择分析
① 数据标准化处理.利用式(13)对表 1中的fat和fac进行标准化处理,结果如表 2所示.
|
|
表 2 fat和fac标准化后的均值对照表 |
② 分别为标准化后的fat和fac赋予决策者偏好系数α和(1-α),利用式(14)使其转化为单一的决策目标.如:取w1=0.1、w2=0.9时,有
| $ \begin{array}{*{20}{c}} {{f_{\left( {0.1,0.9} \right)}}\left( {{A_1}} \right) = \alpha {R_{1\left( {0.1,0.9} \right)}}\left( {{A_1}} \right) + }\\ {\left( {1 - \alpha } \right){R_{2\left( {0.1,0.9} \right)}}\left( {{A_1}} \right) = 0.496\alpha + 0.503\left( {1 - \alpha } \right)} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {{f_{\left( {0.1,0.9} \right)}}\left( {{A_2}} \right) = \alpha {R_{1\left( {0.1,0.9} \right)}}\left( {{A_2}} \right) + }\\ {\left( {1 - \alpha } \right){R_{2\left( {0.1,0.9} \right)}}\left( {{A_2}} \right) = 0.504\alpha + 0.497\left( {1 - \alpha } \right)} \end{array} $ | (16) |
③ 利用加权函数公式确定α在某种范围取值时,哪种算法在求解时更有优势.如:取w1=0.1、w2=0.9时,当α∈[0, 0.429]时,f(A2)值最优,即应选择改进遗传退火算法进行求解;当α∈(0.429, 1]时,f(A1)值最优,即应选择遗传算法进行求解.
3) 基于云制造平台的供应链生产计划方案制定
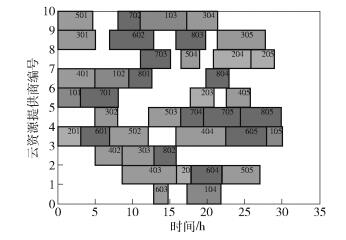
取w1=0.9、w2=0.1的权重组合,且决策者偏好α=0.15,则可选择改进遗传退火算法来为基于云制造平台的供应链制定生产计划,甘特图如图 1所示.
|
图 1 改进遗传退火算法计算得到的甘特图 |
基于云制造平台供应链的部分生产计划如下.
① 云资源提供商7为子任务401、102、801和804提供服务,其服务的时间区间分别为[0, 5]、[5, 9.54]、[9.54, 12.54]和[19.84, 22.84].
② 云资源提供商3为子任务402、303和802提供服务,其服务的时间区间分别为[5, 8.63]、[8.63, 12.84]和[12.84, 15.84].
③ 云资源提供商2为子任务403、202、604和505提供服务,其服务的时间区间分别为[8.63, 15.81]、[15.81, 17.81]、[17.81, 21.98]和[21.98, 27.09].
④ 云资源提供商4为子任务201、601、502、404、605和105提供服务,其服务的时间区间分别为[0, 3]、[3, 7]、[7, 12.11]、[15.81, 22.51]、[22.51, 27.97]和[27.97, 30.07].
关键路径的子任务执行顺序为401→402→403→404→605→105,最大完工时间的最优值是30.07h.
5 结束语以云制造平台为调度主体,构建了以最大完工时间、总服务成本和总运输成本最小为优化目标的供应链生产计划模型,并设计了2种启发式算法用于模型求解.构建了基于最大完工时间和总成本的算法选择模型,决策者可根据自身偏好选择最优的求解算法.该研究可为以云制造平台为调度主体的供应链制定合理的生产计划.
| [1] |
肖莹莹, 李伯虎, 庄长辉, 等. 面向用户多品种定制的分布式供应链调度[J]. 计算机集成制造系统, 2015, 21(3): 800–812.
Xiao Yingying, Li Bohu, Zhuang Changhui, et al. Distributed supply chain scheduling oriented to multi-variety customization[J]. Computer Integrated Manufacturing Systems, 2015, 21(3): 800–812. |
| [2] |
熊永华, 王静, 吴敏, 等. 面向多目标优化的云制造虚拟资源调度方法[J]. 计算机集成制造系统, 2015, 21(11): 3079–3087.
Xiong Yonghua, Wang Jing, Wu Min, et al. Virtual resource scheduling method of cloud manufacturing oriented to multi-objective optimization[J]. Computer Integrated Manufacturing Systems, 2015, 21(11): 3079–3087. |
| [3] | Pérez-Lechuga G, Flores-Rivera C F, Karelyn A A, et al. A multi period stochastic model to link the supply chain with the production plan in a manufacturing organization[J]. Advances & Applications in Statistical Sciences, 2011, 6(6): 255–283. |
| [4] | Hassanzadeh S. A cloud manufacturing based approach to suppliers selection and its implementation and application perspectives[D]. London: Brunel University London, 2016. |
| [5] | Liu Y, Xu X, Zhang L, et al. Workload-based multi-task scheduling in cloud manufacturing[J]. Robotics and Computer-Integrated Manufacturing, 2016, 45(3): 3–20. |


