2. 北京工业大学 北京未来网络科技高精尖创新中心, 北京 100124;
3. 中国科学院 计算技术研究所, 北京 100190
为解决超限学习机复杂度较高的问题,提出了一种新型的超限学习机更新策略,称为序列超限学习机.避免了复杂度较高的逆矩阵运算,而且能够应用于嵌入式系统中.序列超限学习机比各种广泛应用的机器学习分类器具有更低的计算复杂度.基于实际数据集的仿真结果表明,序列超限学习机的分类精度比传统超限学习机和其他广泛应用的分类器更高,而且具有更短的训练时间.
2. Beijing Advanced Innovation Center for Future Internet Technology, Beijing University of Technology, Beijing 100124, China;
3. Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China
Extreme learning machine (ELM) achieves faster training speed and higher classification accuracy, compared with other widely used classifiers, such as back propagation (BP), support vector machine (SVM), spectral clustering (SC), and so forth. However, ELM suffers from some drawbacks:1) ELM utilizes the calculation of inverse matrix for training, which cannot be adopted in the embedded system; 2) the training time of ELM increases dramatically for large-scale applications. To solve these drawbacks of ELM, a new training strategy called Sequential ELM (SELM) was proposed, which avoids the calculation of inverse matrix. Therefore, SELM can be adopted in the embedded system. It is proven that SELM achieves lower complexity than other widely used algorithms. Furthermore, simulations based on practical datasets indicate that the classification accuracy of SELM is higher than traditional ELM and other widely used classifiers with shorter training time.
机器学习算法的突出优点是能够逼近复杂的非线性函数,而且具有并行性好、快速适应性,近年来在诸多领域得到了广泛的应用[1],而且能够处理许多传统方法无法处理的分类问题.反向传播算法[1]、支持向量机[2]和谱聚类[3]是最常见的机器学习分类算法.这些算法虽然得到了广泛的应用,但也存在一些共同的缺点:1)容易得到局部最优解;2)算法复杂度较高.这些不足限制了传统机器学习分类算法的应用.所以需要提出新的分类算法以弥补传统机器学习分类算法的不足.
针对上述分类算法的缺点,黄广斌等提出了超限学习机(ELM, extreme learning machine) [1].传统单层神经网络的隐藏层权重是由梯度下降等方法计算得到,而超限学习机的隐藏层权重是随机产生的,这大大缩短了训练时间[1].然而传统超限学习机也具有如下缺点:1)训练阶段需要计算逆矩阵,无法应用于嵌入式系统中; 2)随着训练数据量的增加,传统超限学习机的训练时间将会快速上升,无法处理大数据量的应用.另外,超限学习机存在许多改良算法. Wang等[4]提出了有效超限学习机,该算法选取特定的隐藏层参数,使隐藏层矩阵满秩,仿真证明其分类精度比传统超限学习机更高. Liu等[5]提出了半监督超限学习机,在训练神经网络之前,半监督超限学习机对训练数据进行聚类,从而提高了分类精度.然而上述超限学习机的改良算法在传统超限学习机优化方程的基础上,仅仅更改了目标函数或者增加了约束条件,却仍然需要计算逆矩阵,和传统超限学习机具有相同的缺点.
针对传统分类算法和基于超限学习机的各种算法的缺点,提出了一种低复杂度的超限学习机训练策略,称为序列超限学习机(SELM, sequential ELM).序列超限学习机采用了不同的训练策略序列,亦即对于超限学习机的优化方程采用了不同的求解方法,避免了逆矩阵的计算,使得超限学习机可以应用于嵌入式系统中,这是许多传统机器学习分类器无法做到的.可证明,和传统的基于机器学习的分类器相比,序列超限学习机具有更低的算法复杂度.基于实际数据集的实验结果表明,序列超限学习机具有较高的分类精度和较短的训练时间.
1.1 超限学习机介绍设g表示激活函数,wl表示第l个隐藏节点和输入节点之间的权重,bl表示第l个隐藏节点和输入节点之间的偏置.其中wl、bl(l=1, 2, …, L)由任意连续分布的函数产生[6-7].其隐藏层输出矩阵为
超限学习机的训练过程可表示为如下优化问题:
| $ \mathop {{\rm{minimize}}}\limits_\mathit{\boldsymbol{\beta }} C'\left\| {\mathit{\boldsymbol{T}} - \mathit{\boldsymbol{H\beta }}} \right\|_{\rm{F}}^2 + \left\| \mathit{\boldsymbol{\beta }} \right\|_{\rm{F}}^2 $ | (1) |
其中‖·‖F表示Frobenius范数,设输出层的权重矩阵为
| $ \mathit{\boldsymbol{\beta }} = {\left( {\frac{1}{{C'}}\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{T}} $ | (2) |
其中I∈RL×L表示单位矩阵.在训练阶段,固定隐藏层节点数、隐藏层参数wl、bl(l=1, 2, …, L)和输出权重β.验证阶段隐藏层输出矩阵H′={h′nl}可以表示h′nl=g(wlTx′n+bl),其中x′n(n=1, 2, …, N)表示验证阶段的输入数据.
1.3 超限学习机算法复杂度隐藏层输出矩阵H的计算复杂度为
| $ {T_H} = O\left( {{N_0}NL} \right) $ | (3) |
其中:N0和N分别表示训练数据和训练目标的数;L表示神经网络隐藏层节点的数.然后需要
| $ {T_{{\rm{ELM}}}} = {T_H} + O\left( {{S_1} + {S_2} + {S_3}} \right) = O\left( {N{L^2} + NML + {N_0}NL} \right) $ | (4) |
序列超限学习机逐行更新输出权重矩阵.在训练阶段,定义误差矩阵
| $ \mathop {{\rm{minimize}}}\limits_{\mathit{\boldsymbol{\beta }} = {{\left[ {{\mathit{\boldsymbol{\beta }}_1},{\mathit{\boldsymbol{\beta }}_2}, \cdots ,{\mathit{\boldsymbol{\beta }}_L}} \right]}^{\rm{T}}}} C\left\| {{\mathit{\boldsymbol{E}}_l} - {\mathit{\boldsymbol{h}}_l}\mathit{\boldsymbol{\beta }}_l^{\rm{T}}} \right\|_{\rm{F}}^2 + \sum\limits_{l = 1}^L {\left\| {{\mathit{\boldsymbol{\beta }}_l}} \right\|_2^2} $ | (5) |
其中‖·‖2表示l2范数.式(5)代入KKT条件,有
| $ {\nabla _{{\mathit{\boldsymbol{\beta }}_l}}}\left( {C\left\| {{\mathit{\boldsymbol{E}}_l} - {\mathit{\boldsymbol{h}}_l}\mathit{\boldsymbol{\beta }}_l^{\rm{T}}} \right\|_{\rm{F}}^2 + \sum\limits_{l = 1}^L {\left\| {{\mathit{\boldsymbol{\beta }}_l}} \right\|_2^2} } \right) = 0 $ | (6) |
通过计算式(6),βl(l=1, 2, …, L)可以表示为
| $ {\mathit{\boldsymbol{\beta }}_l} = {\left( {{C^{ - 1}} + \mathit{\boldsymbol{h}}_l^{\rm{T}}{\mathit{\boldsymbol{h}}_l}} \right)^{ - 1}}\mathit{\boldsymbol{E}}_l^{\rm{T}}{\mathit{\boldsymbol{h}}_l} $ | (7) |
综合上述分析可知,训练阶段的流程如下:
1) 初始化阶段.随机产生隐藏层参数wl、bl,设定门限值ε;
2) 计算隐藏层权重矩阵H;
3) 对于l=1, 2, …, L,有
a) 计算误差矩阵
b) 通过式(7)更新输出权重的第l列βl;
c) 如果
4) 返回输出层权重β.
验证阶段的流程如下:
1) 固定参数wl、bl(l=1, 2, …, L)及输出权重β;
2) 计算隐藏层权重H′;
3) 计算输出矩阵O′=H′β.
序列超限学习机仅需要简单地四则运算,适用于嵌入式系统中.由下文的分析以及实验结果可知,序列超限学习机算法复杂度低,分类准确性高.这是由于传统超限学习机训练时,所有输出层权重同时更新,这导致某个隐藏层节点的扰动会扩散到整个输出层权重中,而序列超限学习机的输出层权重是逐行更新的,某个隐藏层节点的扰动只会影响与之连接的输出层权重,不会扩散到整个输出层权重中.
2.2 序列超限学习机算法复杂度序列超限学习机误差矩阵
| $ \begin{array}{*{20}{c}} {{T_{{\rm{SELM}}}} = O\left( {{S_H} + {S_{{\beta _1}}} + {S_{{E_1}}} + \left( {L - 1} \right)\left( {{S_{{\beta _l}}} + {S_{{E_l}}}} \right)} \right) = }\\ {O\left( {NML + {N_0}NL} \right)} \end{array} $ | (8) |
下面,给出并且证明了定理1.
定理1 如果隐藏层节点数L和类的数M满足不等式
将不等式
由定理1可知,如果有足够的隐藏层节点,那么序列超限学习机比传统超限学习机的复杂度更低.
3 常用分类器算法复杂度对比 3.1 支持向量机的算法复杂度二分类支持向量机复杂度为Tbin=O(N3+N0N2),其中N0是输入数据的维度[9].多分类问题有2种策略:一对多策略(OVA, one versus all)和一对一策略(OVO, one versus one)[2]. OVA解M(M-1)/2个二分类问题.训练数据数目N通常远大于L、M、N0[8],OVA复杂度为
| $ {T_{{\rm{OVA}}}} = O\left( {M{N^3} + {N_0}M{N^2}} \right) = O\left( {{N^3}} \right) $ |
第m (m=1, 2, …M)类有Nm个数据.则OVO复杂度为
| $ {T_{{\rm{OVO}}}} = \sum\limits_{1 \le i < j \le N} {O\left( {{{\left( {{N_i} + {N_j}} \right)}^3}} \right)} $ |
| $ {T_{{\rm{OVO}}}} \le \sum\limits_{1 \le i < j \le M} {O\left( {N_i^3 + N_j^3} \right)} \le O\left( {M{N^3} + {N_0}M{N^2}} \right) $ | (9) |
故OVO复杂度
| $ {T_{{\rm{OVO}}}} = O\left( {M{N^3} + {N_0}M{N^2}} \right) = O\left( {{N^3}} \right) $ |
由于谱聚类算法(SC, spectral clustering)计算邻接矩阵的复杂度为Tadj=O(N0N2)[3].邻接矩阵奇异值分解的复杂度为TSVD=O(N3+N0L2+N02L)[3].故谱聚类的算法复杂度为TSC=Tadj+TSVD=O(N3).
3.3 有效超限学习机的算法复杂度下面对效超限学习机(EELM, effective ELM)的算法复杂度进行分析.设
| $ {T_{{\rm{EELM}}}} = {T_H} + {T_{{\rm{ELM}}}} + {T_{{\rm{extra}}}} = O\left( {{N^2} + N{L^2} + NML + {N_0}NL} \right) $ | (10) |
下面分析计算半监督超限学习机(USELM, unsupervised ELM)[5]的复杂度.设W={wij}表示相似度矩阵,第(i, j)个元素为
| $ {w_{ij}} = \exp \left( { - 2{\sigma ^{ - 2}}\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|_2^2} \right) $ |
其中σ表示输入数据x1, x2, …, xN的标准差.训练输出矩阵需要计算
| $ {T_W} = \frac{1}{2}N\left( {N + 1} \right){T_{{w_{ij}}}} = \frac{1}{2}N\left( {N + 1} \right)\left( {3{N_0} + 1} \right) $ | (11) |
计算γ和ν的复杂度为Teig=O(N3)[10].半监督超限学习机的复杂度为
| $ {T_{{\rm{USELM}}}} = {T_{{\rm{ELM}}}} + {T_W} + {T_{{\rm{eig}}}} = O\left( {{N^3}} \right) $ |
综上可得,各种算法的复杂度如表 1所示.
|
|
表 1 各种算法的复杂度 |
通过表 1可以发现,支持向量机[2]、谱聚类[3]、有效超限学习机[4]、半监督超限学习机[5]的算法复杂度比序列超限学习机的算法复杂度高.另外,定理1已经证明,在满足一定条件的情况下,系列超限学习机的算法复杂度比传统超限学习机更低.而且定理1需要的条件在实际应用中很容易满足.在实际应用中,序列超限学习机的算法复杂度不仅比支持向量机、谱聚类等传统分类算法低,也比传统超限学习机及其改进算法,如有效超限学习机、半监督超限学习机等的复杂度低.
4 仿真实验和分析下面将序列超限学习机的效果与其他算法进行对比.支持向量机和谱聚类的效果比反向传播算法更好[2-3],所以选择支持向量机和谱聚类算法作为对比.超限学习机的改进算法中,选择半监督超限学习机和有效超限学习机算法.选择基于真实数据,将广泛应用的UCI数据集[11]在Matlab 2016b上运行,中央处理器主频为2.40GHz.每组仿真进行了1000次,并且求取平均值.选择sigmoid函数作为激活函数,各数据集的特性如表 2所示.
|
|
表 2 数据集特性 |
基于表 2中的数据集,对各种分类器的效果进行了对比,分类效果如表 3所示.可以发现,基于超限学习机的各种算法,即序列超限学习机、传统超限学习机、有效超限学习机和半监督超限学习机算法的分类效果比支持向量机和谱聚类的分类效果好.而基于超限学习机的各种算法中,序列超限学习机的算法精度比其他几种基于超限学习机的算法的分类精度更高,这意味着序列超限学习机可有效地应用于分类问题中.
|
|
表 3 各种分类器的分类准确度对比 |
不同分类器的训练时间如表 4所示,序列超限学习机的训练时间比其他各种分类器的训练时间少.这验证了对各种算法复杂度的分析结果,序列超限学习机可以处理大数据量分类问题.
|
|
表 4 各种分类器的训练时间对比 |
通过表 3和表 4可以发现,基于超限学习机的各种分类器(序列超限学习机、传统超限学习机、半监督超限学习机以及有效超限学习机)在分类精度和训练时间方面,比支持向量计算法、谱聚类算法、超限学习机及其改进算法都具有更好的效果.
下面分析基于超限学习机的不同分类器的性能差异.首先分析基于超限学习机各种算法的收敛性,采用Human数据集,分析基于超限学习机的各种分类器的分类效果和隐藏层节点数之间的关系.图 1所示为不同分类器的分类效果和隐藏层节点数之间的关系,用以衡量不同分类器的收敛性.可以发现,序列超限学习机算法的收敛速度和半监督超限学习机相近,而且序列超限学习机的收敛速度比半监督超限学习机的收敛速度更快.实际上,针对表 3和表 4中其他数据集进行的测试得到了和Human数据集类似的结果.由于隐藏节点数大于200的情况下,序列超限学习机具有较好的分类效果,所以隐藏节点数选择为L≥200.
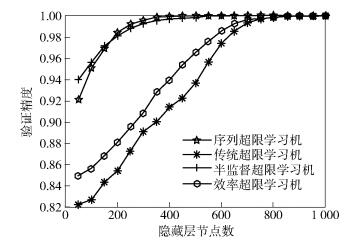
|
图 1 分类精度和隐藏层节点数的关系 |
传统超限学习机的收敛速度比序列超限学习机慢,这是因为传统超限学习机需要将整个隐藏层输出矩阵β视为整体进行计算,这使得某个节点上的误差和扰动会扩散到所有神经网络的隐藏层节点.
4.4 训练时间和隐藏层节点数的关系不同算法的复杂度对比如图 2所示.相同隐藏层节点数的情况下,序列超限学习机的训练时间比其他算法更少.这验证了上文中对于各种算法复杂度的分析结果.根据实验结果以及定理1的结论,为了使得序列超限学习机比其他基于超限学习机的分类器具有更少的训练时间,选择L≥200.
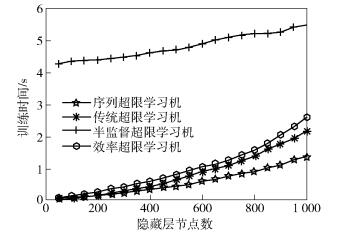
|
图 2 训练时间和隐藏层节点数的关系 |
通过图 1和图 2的分析,在提高分类精度的情况下,为了尽量降低训练时间,选择L=200.通过图 1和图 2的结果可见,为了达到相同的分类精度,序列超限学习机所需要的节点数比其他基于超限学习机的分类器更少.由于序列超限学习机避免了逆矩阵的计算,所以可以应用于嵌入式系统中.
5 结束语提出了一种新型的超限学习机训练方法,称为序列超限学习机.证明了序列超限学习机的复杂度比传统超限学习机以及各种常用分类器的复杂度更低,而且基于真实数据(UCI数据集)的实验证明了上述结论.序列超限学习机的输出矩阵是逐行更新的,避免了传统超限学习机的逆矩阵运算,所以能够应用于嵌入式系统中,且具有更低的复杂度.与广泛应用的数据集相比序列超限学习机的分类效果更好,收敛速度更快,训练时间更短.所以序列超限学习机能够得到更加广泛的研究和应用.
| [1] | Tang Jiexiong, Deng Chenwei, Huang Guangbin. Extreme learning machine for multilayer perceptron[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(4): 809–821. doi: 10.1109/TNNLS.2015.2424995 |
| [2] | Chakrabarty A, Buzzard G T, Z·ak S H. Output-tracking quantized explicit nonlinear model predictive control using multiclass support vector machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 4130–4138. doi: 10.1109/TIE.2016.2638401 |
| [3] | Yang Yang, Shen Fumin, Huang Zi, et al. Discrete nonnegative spectral clustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(9): 1834–1845. doi: 10.1109/TKDE.2017.2701825 |
| [4] | Huang Gao, Huang Guangbin, Song Shiji, et al. Trends in extreme learning machines:a review[J]. Neural Networks, 2015, 61(Supplement C): 32–48. |
| [5] | Liu Tianchi, Yang Yan, Huang Guangbin, et al. Driver distraction detection using semi-supervised machine learning[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(4): 1108–1120. doi: 10.1109/TITS.2015.2496157 |
| [6] | Jin Bo, Jing Zhongliang, Zhao Haitao. Incremental and decremental extreme learning machine based on generalized inverse[J]. IEEE Access, 2017(5): 20852–20865. |
| [7] | Zhang Lei, Zhang David. Evolutionary cost-sensitive extreme learning machine[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(12): 3045–3060. doi: 10.1109/TNNLS.2016.2607757 |
| [8] |
刘渭滨, 邹智元, 邢薇薇. 模式分类中的特征融合方法[J]. 北京邮电大学学报, 2017, 40(4): 1–8.
Liu Weibin, Zou Zhiyuan, Xing Weiwei. Feature fusion methods in pattern classification[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(4): 1–8. |
| [9] | Huang Kaizhu, Jiang Haochuan, Zhang Xuyao. Field support vector machines[J]. IEEE Transactions on Emerging Topics in Computational Intelligence, 2017, 1(6): 454–463. doi: 10.1109/TETCI.2017.2751062 |
| [10] | Kuang Kelvin, Lee Chi, Chen Chiaoen. An eigen-based approach for enhancing matrix inversion approximation in massive MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 5480–5484. doi: 10.1109/TVT.2016.2622010 |
| [11] | Zhang Xianchao, Zong Linlin, Liu Xinyue, et al. Constrained clustering with nonnegative matrix factorization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(7): 1514–1526. doi: 10.1109/TNNLS.2015.2448653 |


