2. 华为技术有限公司 2012实验室, 广东 深圳 518129
针对多输入多输出(MIMO)-正交频分复用(OFDM)系统,提出了功率控制与波束赋形的联合优化算法,采用更加符合实际系统的干扰模型,将节能问题建模为功率控制与波束赋形的联合优化问题.为了求解上述非凸问题,基于上下行对偶原理和标准干扰函数理论,提出一种两阶段解决方案,并给出相应的理论证明该方案的收敛性.仿真结果表明,所提算法在多天线场景下相对于现有算法有更快的收敛速率,与传统的波束赋形方案相比,具有更低的能耗.
2. 2012Lab, Huawei Technologies, Guangdong Shenzhen 518129, China
A joint optimization problem of power control and beamforming for multiple input multiple output (MIMO)-orthogonal frequency division multiplexing (OFDM) system with more realistic interference model was proposed. Then a two-stage scheme based on dual of uplink-downlink and standard interference mapping theory was given to solve this problem, which is proved to be rigorously convergent. Simulations show that the proposed scheme converges faster in multiple-antenna cases and the proposed algorithm outperforms the traditional ones in terms of power saving.
基站系统的节能技术已成为下一代无线网络必不可少的技术之一[1-4].对于多输入多输出(MIMO, multiple input multiple output)天线系统的节能问题, 以往的文献研究最优的波束赋形问题[5-7]. Chen等[5]采用半正定规划的方法,在多天线系统信道状态信息存在误差的情况下,针对带鲁棒性的功率控制进行研究;基于网络的上-下行对偶原理,在满足多用户MIMO中所有用户的信干噪比(SINR, signal to interference plus noise ratio)的条件下,Song等[6]研究波束赋形和功率控制的联合优化问题;在满足用户的SINR需求的条件下,Bjornson等[7]对如何最优化波束赋形因子的各种算法进行调研和总结.上述文献中的SINR模型主要是针对MIMO系统,均没有考虑正交频分复用(OFDM, orthogonal frequency division multiplexing system)系统中小区负载大小对小区间干扰的影响.
针对MIMO-OFDM系统,笔者考虑更为接近实际系统的干扰模型,在满足用户的服务质量(QoS, quality of service)和小区负载约束的前提下,最优化基站总的传输功率与波束赋形因子.
1 功率控制与波束赋形联合优化 1.1 系统模型考虑由M个小区和N个用户组成的无线网络.小区与用户的集合分别表示为
| $ {y_{i,j}} = \sqrt {{P_i}} \mathit{\boldsymbol{h}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}{\mathit{\boldsymbol{s}}_{i,j}} + \underbrace {\sum\limits_{k \ne i}^M {\sqrt {{P_k}} \mathit{\boldsymbol{h}}_{k,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{k,j}}{\mathit{\boldsymbol{s}}_{k,j}}} }_{邻区间干扰} + {\upsilon _j} $ | (1) |
其中:第2项为小区间的干扰,即邻区干扰,υj为加性高斯白噪声,其均值为0,方差为σj2.假设si, j为统计独立信号,其均值为0且功率为E{|si, j|2}=1, ∀i, j,则小区i与用户j间的SINR可表示为Si, j
| $ {S_{i,j}} = \frac{{{{\left| {\sqrt {{P_i}} \mathit{\boldsymbol{h}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}} \right|}^2}}}{{\sum\limits_{k \ne i}^M {{\rho _k}{{\left| {\sqrt {{P_k}} \mathit{\boldsymbol{h}}_{k,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{k,j}}} \right|}^2}} + \sigma _j^2}} $ | (2) |
其中ρi为小区i的负载因子,将在式(4)中对其进行定义,则每个时频资源(RB, resource block)的传输速率
| $ {{\tilde f}_{i,j}} = B{\rm{lb}}\left( {1 + {S_{i,j}}} \right) $ | (3) |
其中B为每个RB的带宽.假设fi, j为基站i与用户j间的传输速率需求,则负载因子可表示为
| $ {\rho _i} = \sum\limits_{j = 1}^{{N_i}} {{\rho _{i,j}}} = \sum\limits_{j = 1}^{{N_i}} {\frac{{{f_{i,j}}}}{{K{{\tilde f}_{i,j}}}}} ,\forall i \in \mathscr{M} $ | (4) |
其中K为每个小区内总的RB数.
笔者研究在满足用户速率需求和小区负载约束的情况下,联合优化基站的传输功率与波束赋形因子.可将问题建模为
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{w,P} \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^{{L_i}} {{\rho _i}{P_i}{{\left\| {{\mathit{\boldsymbol{w}}_{i,j}}} \right\|}^2}} } }\\ {{\rm{s}}.{\rm{t}}.\;{f_{i,j}} \ge {\gamma _{i,j}},\forall i,j}\\ {{\rho _i} \le {{\bar \rho }_i},\forall i} \end{array} $ | (5) |
上述模型中,γi, j表示用户j由基站i服务的速率需求,ρ表示基站i所能承受的最大负载,第1个约束表示满足所有用户的速率需求,第2个约束表示负载约束,即实际的负载占用率不能超过实际基站的能力上限.此优化问题与文献[5-7]是不同的,文献[5-7]中的SINR模型均不考虑负载因子对SINR的影响,也与文献[8]中的不同,其作者只考虑了单天线的场景.
1.2 两阶段方案式(2)所示的SINR和式(4)所示的负载因子均为非凸函数,所以式(5)为一非凸问题.因此式(5)不能采用经典的凸优化理论进行求解.为了使其便于求解,提出两阶段求解模型.
如图 1所示,在每个循环的第1阶段,首先假设功率因子Pi为已知,通过解波束赋形问题得到wi, j;接着,在第1阶段的基础上,通过优化相应问题可得到Pi.若干次循环后,可达到优化问题的收敛点,同时输出最终的波束赋形因子P*、w*.当然,该方案能否收敛需要严格的数学证明.在下面的叙述中,将给出详细的求解过程,并证明所提出的算法确实能收敛到相应的固定点.上述的第1阶段可称为波束赋形阶段,该阶段的目的是在保持发射功率不变的条件下最小化小区间的干扰;第2阶段可称为功率控制阶段,该阶段的目的则是在保证用户QoS需求的同时,最小化基站的发射功率.不失一般性,下面均假设‖wi, j‖2=1.
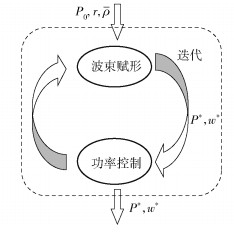
|
图 1 两阶段解决方案示意图 |
1) 波束赋形阶段:第1阶段的波束赋形问题可建模为
| $ \begin{array}{l} \mathop {\max }\limits_w {S_{i,j}}\\ {\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{i,j}} = 1,\forall i,j \end{array} $ | (6) |
由式(6)可知,最大化Si, j同时保持有用信号等于一定值,可等效为最小化干扰加白噪声的总功率.干扰加白噪声的总功率可定义为
| $ {I_{i,j}} = \sum\limits_{k \ne i}^M {{P_k}{\rho _k}\mathit{\boldsymbol{w}}_{k,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{k,j}}\mathit{\boldsymbol{h}}_{k,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{k,j}}} + \sigma _j^2 $ | (7) |
直接求解式(7)的最小值比较困难,借助于上行-下行对偶原理[9],可将式(6)转化为
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_\mathit{\boldsymbol{w}} S_{i,j}^{{\rm{UL}}}}\\ {{\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{i,j}} = 1,\forall i,j} \end{array} $ | (8) |
其中Si, jUL可表示为
| $ S_{i,j}^{{\rm{UL}}} = \frac{{{P_i}\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{i,j}}\mathit{\boldsymbol{h}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}}}{{\sum\limits_{k \ne i}^M {{P_k}{\rho _k}\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{i,j}}\mathit{\boldsymbol{h}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}} + \sigma _j^2\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}}} $ | (9) |
同理,式(8)可转化为
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_\mathit{\boldsymbol{w}} I_{i,j}^{{\rm{UL}}} = \sum\limits_{k \ne i}^M {{P_k}{\rho _k}\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{k,j}}\mathit{\boldsymbol{h}}_{k,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}} + \sigma _j^2\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}}\\ {{\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{w}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{i,j}} = 1,\;\;\;\;\;\;\forall i,j} \end{array} $ | (10) |
定义
| $ {\mathit{\boldsymbol{w}}_{i,j}} = \frac{{{{\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{i.j}^{{\rm{UL}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{h}}_{i,j}}}}{{\mathit{\boldsymbol{h}}_{i,j}^{\rm{H}}{{\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{i.j}^{{\rm{UL}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{h}}_{i,j}}}},\forall i,j $ | (11) |
2) 功率控制阶段:在求得波束赋形因子, 即式(11)中的wi, j之后,可将式(5)转化为一个非线性互偶方程,而此类问题可采用标准干扰映射理论来求解.为简化符号,令ρ=[ρ1, …, ρNi]T, P=[P1, …, PM]T, f=[f11, …, f1N1, f21, …, f2N2, …, fMNM]T,式(4)可表示为
| $ \mathit{\boldsymbol{\rho }} = g\left( {\mathit{\boldsymbol{P}},\mathit{\boldsymbol{f}},\mathit{\boldsymbol{\rho }},\mathit{\boldsymbol{w}}} \right) $ | (12) |
为了求解式(5),有以下的扩展命题,此命题是由文献[10]中的定理1直接扩展而来的.
命题1 假设波束赋形因子固定,且所有基站的负载上限是可达的,则最优的功率解Pi(
从命题1可知,式(5)的最优解可通过求式(12)获得.然而,式(12)是一个难以求解的非线性函数,并且它是功率Pi(
| $ \begin{array}{*{20}{c}} {{\varphi _i}\left( {\mathit{\boldsymbol{P}},\mathit{\boldsymbol{f}},\mathit{\boldsymbol{\rho }},\mathit{\boldsymbol{w}}} \right) = }\\ {\left\{ \begin{array}{l} \frac{{{P_i}}}{{{\rho _i}}}\sum\limits_{j = 1}^{{N_i}} {\frac{{{f_{i,j}}}}{{BK{\rm{lb}}\left( {1 + {S_{i,j}}} \right)}},} \;\;\;{P_i} \ne 0\\ \begin{array}{*{20}{c}} {\frac{{\ln 2}}{{{\rho _i}BK}}\sum\limits_{j = 1}^{{N_j}} {\frac{{{f_{i,j}}}}{{{{\left| {\mathit{\boldsymbol{h}}_{i,j}^{\rm{H}}{\mathit{\boldsymbol{w}}_{i,j}}} \right|}^2}}}\left( {\sum\limits_{k \ne i}^M {{\rho _k}{P_k}{{\left| {\mathit{\boldsymbol{w}}_{k,j}^{\rm{H}}{\mathit{\boldsymbol{h}}_{k,j}}} \right|}^2}} + \sigma _j^2} \right)} ,}\\ {{P_i} = 0} \end{array} \end{array} \right.} \end{array} $ | (13) |
定义Ψ=[φ1, …, φM],从文献[12]可知其为一个标准干扰函数.当fi, j=γi, j, ρi=ρi时,上述方程可以直接求解,进而式(5)可求解,其求解过程见算法1.
算法1 功率控制算法
步骤1 初始化γ、ρ,发射功率为P=P0=[0, …, 0]T和ε(如取值为10-2);
步骤2 求解式(8)得到w0*;
步骤3 采用式
步骤4 求解式(8)可得到wn+1*;
步骤5 当‖wn+1*-wn*‖≤ε, 或‖Pn+1*-Pn*‖≤ε时,则退出算法;否则返回步骤3.
以下命题是对算法1收敛性的严格证明.
命题2 当fi, j=γi, j, ρi=ρi时,式(13)的固定点是唯一的,且所提算法的波束赋形因子也是唯一的.
证明 对于给定任意wi, j, ∀i, j,由文献[10]中的Lemma 1可知,Ψ是一个标准干扰函数.由标准干扰函数的性质,可知其有唯一的固定点
命题3 传输功率{Pnk}是一个非减序列,而且能收敛到唯一的固定点Pn*,即Ψ(Pn*, γ, ρ, wn*)=Pn*.
证明 首先,通过归纳法证明{Pnk}为一个非减序列.由算法1可知Pn0=P0=[0, …, 0]T,Pn1=Ψ(Pn0, γ, ρ, wn*)≥P0.由函数Ψ(Pn1, γ, ρ, wn*)的非负性,可得到Pn1≥P0.假设Pnk≥Pnk-1,由标准干扰函数的单调性[12],可得到Pnk+1=Ψ(Pnk, γ, ρ, wn*)≥Ψ(Pnk-1, γ, ρ, wn*)=Pnk,即Pnk+1≥Pnk,故算法1生成的序列{Pnk}为非减序列.由于wn*的最优性,则可得{Pnk}的极限存在,假设极限为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat P}} = \mathop {\lim }\limits_{k \to \infty } \mathit{\boldsymbol{P}}_n^k = \mathop {\lim }\limits_{k \to \infty } \mathit{\Psi }\left( {\mathit{\boldsymbol{P}}_n^{k - 1},\mathit{\boldsymbol{\gamma }},\mathit{\boldsymbol{\rho }},\mathit{\boldsymbol{w}}_n^ * } \right) = }\\ {\mathit{\Psi }\left( {\mathop {\lim }\limits_{k \to \infty } \mathit{\boldsymbol{P}}_n^{k - 1},\mathit{\boldsymbol{\gamma }},\mathit{\boldsymbol{\rho }},\mathit{\boldsymbol{w}}_n^ * } \right) = \mathit{\Psi }\left( {\mathit{\boldsymbol{\hat P}},\mathit{\boldsymbol{\gamma }},\mathit{\boldsymbol{\rho }},\mathit{\boldsymbol{w}}_n^ * } \right)} \end{array} $ | (14) |
故可得到
命题4 命题1求解过程中步骤3中的等式
证明 采用与命题3类似的证明过程,可证明序列{Ψ(Pnk, γ, ρ, wn*)}也是非减序列,即等价于序列{Pnk}为非递减的.由于式(12)为一个连续函数,则由命题3可得到
命题5 算法1是收敛的,而且能收敛到固定点.
证明 由上述的证明可知,当k→∞时,序列{Pnk}收敛于Pn*,再根据式(11)可计算得到wn+1*.由于波束赋形能降低干扰,所以对于下一轮的功率控制,可以保证其发射功率比上一次迭代得到降低,即Pn+1*≤Pn*,又Pn+1*=Ψ(Pn*, γ, ρ, wn*)为Pn*的标准干扰函数,而且{Ψ(Pnk, γ, ρ, wn*)}≥0,由此可得到序列{Pn*}为一递减的非负序列,故其一定收敛.由标准干扰函数的性质,其一定收敛到Ψ(Pn*, γ, ρ, wn*)的固定点,即Ψ(P*, γ, ρ, wn*)=P*.
1.3 复杂度分析分析算法1,可知算法主要的计算过程包括一层内迭代和一层外迭代.第p次内迭代包括计算步骤2和多次计算步骤3,步骤2算法的复杂度主要体现在计算矩阵Φi, jUL的逆,其复杂度为
采用3GPP推荐的仿真场景[12],仿真场景是由3个基站组成的网络,基站的最大发射功率为40 W.每个基站服务的用户数为10,且用户位置均匀分布.不失一般性,假设所有用户的速率需求相同,即γi, j=γ.大尺度衰落(包括路损和阴影)和小尺度衰落分别采用文献[12]中的模型和瑞利分布模型,其他仿真参数如表 1所示.
|
|
表 1 仿真参数 |
图 2和图 3显示的是平均总传输功率在不同传输天线场景的变化情况.由图 2可以看出,当ρ={0.4, 0.5, 0.6}时,单天线的基站不能支持γ=600 kbit/s的速率进行传输,因为3个基站所需要的传输功率已经超过总的最大发射功率120 W.而由图 3可以看出,多天线场景的基站能在满足用户QoS需求的同时大大降低基站的传输功率.特别是64天线的场景,在用户速率需求为600 kbit/s时,基站的发射功率仅为0.35 W左右,其所需的发射功率小于单天线发射功率的1/64.由仿真结果可以看出,发射功率下降的趋势与天线数目(增加)的关系不再是线性关系,而是超线性关系.这种超线性关系随着天线数目的增加变得更为明显.由于受限于篇幅,其他仿真结果就不在此一一列出了.
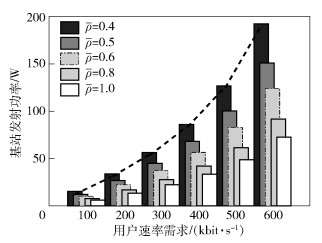
|
图 2 基站(单天线)发射功率与用户速率需求的关系 |
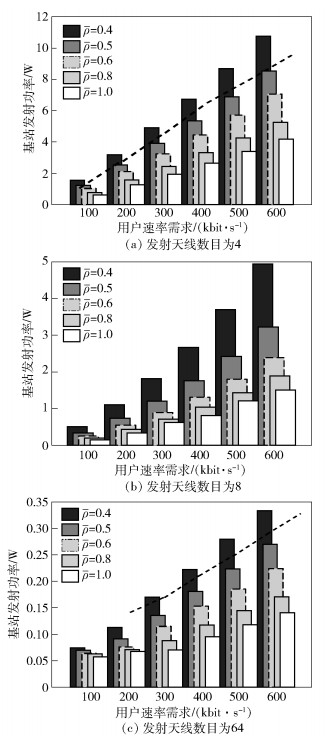
|
图 3 基站(多天线)发射功率与用户速率需求的关系 |
由图 2和图 3的结果对比可看出,在单天线场景中,基站传输功率随着用户速率需求的变化接近于指数方式的增长,这种趋势在负载较轻时特别明显,如ρ=0.4.而在多天线场景,基站传输功率与用户速率需求接近于线性关系,天线数目越多,这一趋势越明显.仿真结果表明,为了满足用户的速率需求与小区的负载限制,多天线更有利于降低基站总的发射功率,这也验证了多天线应用于下一代的无线通信系统可以带来更好的能效.
由图 2和图 3可看出负载的影响在相同用户数、相同用户QoS需求的前提下,无论是单天线还是多天数场景,负载越大,基站发射功率越低,这说明提高小区的负载率能降低系统的能耗.因此,对于MIMO-OFDM系统,提高网络负载也是提升系统能效的手段之一,即通过小区间的负载均衡也可以达到降低系统能耗的目的.
图 4显示的是不同天线数场景的仿真时间对比.可以看出,所提算法在多天线场景的收敛时间更短,原因是多天线场景的迭代次数比单天线场景要少得多,所以多天线场景的计算时间比单天线场景短.注意到128天线场景的仿真时间比64的稍微长一些,这主要是由于128天线场景的迭代次数相对于64天线场景而言下降不多,而由于其天线数目比64天线场景的天线数目多很多,所以,单次迭代计算时间也更长.这使得其最终的收敛时间比64天线场景的长,但128天线的收敛时间也远小于单天线场景.

|
图 4 仿真时间与天线数目的变化关系 |
最后,将所提出的波束赋形算法与传统算法如最大比传输(MRT,maximum ratio transmission)和迫零波束赋形(ZFBF,zero-forcing beamforming)[7, 13]进行对比,如图 5所示.可见,所提的波束赋形算法比传统波束赋形算法更节能,且功率增加的速率相对是最低的.同时,随着天线数目的增加,所提算法相对于ZFBF算法的发射功率差减小,对于天线数目为64的场景,所提的算法与ZFBF的性能差距几乎很小.随着天线数目的增加,ZFBF算法性能渐渐接近理论上的最优波束赋形[7].综上说明,随着天线数目的增加,所提算法性能渐渐接近于理论上的最优,而当天线数目较少时,所提算法的性能优于传统算法,如MRT和ZFBF.
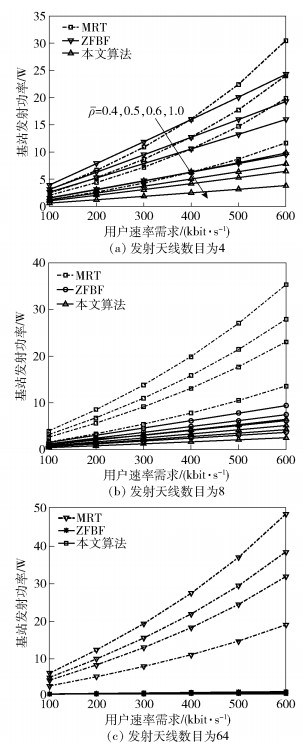
|
图 5 所提出的波束赋形算法与传统波束赋形算法的比较 |
对于MIMO-OFDM场景,采用更为接近实际的干扰模型对能量优化问题进行研究.为了解决功率与波束赋形联合优化的问题,提出两阶段的解决方案,并对所提算法的收敛性给出了数学证明.仿真结果表明,所提算法应用于多天线场景时,与以往的单天线方案相比,收敛速度更快,并且在天线数目比较少时,与传统的MRT、ZFBF算法相比,所提算法有更好的节能性能,而随着天线数目的增加,所提算法的性能渐渐逼近于理论上的最优.所提方案可扩展应用于大规模的MIMO-OFDM技术场景,即下一代无线通信5G.
| [1] |
陈军, 冯穗力, 黄妙娜, 张远见. 多区间功放预失真方案与FPGA实现[J]. 北京邮电大学学报, 2012, 35(1): 90-94.
Chen Jun, Feng Suili, Huang Miaona, et al. Multi-intervals digital predistortion solution on RF amplifier and FPGA implementation[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(1): 90-94. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjyddx201201021 |
| [2] | Yunas S F, Valkama M, Niemela J. Spectral and energy efficiency of ultra-dense networks under different deployment strategies[J]. IEEE Commun Mag, 2015, 53(1): 90–100. doi: 10.1109/MCOM.2015.7010521 |
| [3] | Su Liyan, Yang Chenyang, Xu Zhikun, et al. Energy-efficient downlink transmission with base station closing in small cell networks[C]//Proc IEEE Acoustics, Speech and Signal Processing (ICASSP). Vancouver: [s. n. ], 2013: 4784-4788. |
| [4] |
黄妙娜, 冯穗力, 陈军, 等. LTE网络中多目标优化的动态负载均衡算法[J]. 电子与信息学报, 2014, 36(9): 2152–2157.
Huang Miaona, Feng Suili, Chen Jun, et al. Dynamic load balancing scheme for multi-objective optimization in LTE networks[J]. Jounal of Electronics & Information Technology, 2014, 36(9): 2152–2157. |
| [5] | Chen Jun, Feng Suili, Huang Miaona. Joint antenna selection and robust beamforming design in multi-cell distributed antenna system[J]. China Communication, 2014, 11(4): 85–97. doi: 10.1109/CC.2014.6827571 |
| [6] | Song Bongyong, Cruz R L, Rao B D. Network duality for multiuser MIMO beamforming networks and applications[J]. IEEE Trans Commun, 2007, 55(3): 618–630. doi: 10.1109/TCOMM.2006.888889 |
| [7] | Björnson E, Bengtsson M, Ottersten B. Optimal multiuser transmit beamforming:a difficult problem with a simple solution structure[J]. IEEE Signal Process Mag, 2014, 31(4): 142–148. doi: 10.1109/MSP.2014.2312183 |
| [8] | Ho C K, Di Yuan, Lei Lei, et al. Power and load coupling in cellular networks for energy optimization[J]. IEEE Trans Wireless Commun, 2015, 14(1): 509–519. doi: 10.1109/TWC.2014.2353043 |
| [9] | Tse D, Viswanath P. Downlink-uplink duality and effective bandwidths[C]//Proc IEEE Int Symp Inf Theory (ISIT). Lausanne: [s. n. ], 2002: 52. |
| [10] | Rashid-Farrokhi F, Tassiulas L, Liu K J R. Joint optimal power control and beamforming in wireless networks using antenna arrays[J]. IEEE Trans Commun, 1998, 46(10): 1313–1323. doi: 10.1109/26.725309 |
| [11] | Cavalcante R L G, Pollakis E, Stanczak S. Power estimation in LTE systems with the general framework of interference mappings[C]//Proc IEEE Global Conference on Signal Processing and Information Processing. Atlanta: [s. n. ], 2014: 818-822 |
| [12] | Goldsmith A. Wireless communications[M]. Britain: Cambridge University Press, 2004: 201-320. |


