2. 南昌航空大学 软件学院, 南昌 330063
提出基于超限学习机的链路质量评估方法.选择非对称性指标、信噪比变异系数、均值信噪比为链路质量参数,以包接收率为链路质量评价指标,划分链路质量等级;采用粒子群算法优化超限学习机的输入层权重和偏置参数,构建链路质量评估模型.不同场景下的实验结果表明,与支持向量分类机评估方法相比,所提方法具有更高的评估准确率.
2. School of Software, Nanchang Hangkong University, Nanchang 330063, China
An approach of estimating link quality was proposed which is based on extreme learning machine. The index of link asymmetry, the coefficient of variation of signal to noise ratio and mean signal to noise ratio are chosen as link quality parameters. Link quality level is classified by link packet receive rate which is the evaluation index. Particle swarm optimization algorithm is employed to optimize input weights and offset parameter, so that link quality model is built. In different scenarios, compared with the support vector classification machine estimate methods, the experimental results show that the proposed estimation method achieves better precision.
无线传感器网络(WSNs, wireless sensor networks)是一种由大量部署在监控区域的节点以自组织方式形成的网络,广泛应用于军事、环境监测、交通运输及医疗保健等领域[1].由于受环境噪声和多径效应影响,采用低功率射频通信的节点间链路质量呈现出波动性、非对称性等时空特性,导致节点间通信具有不稳定性,如能有效评估链路质量,不仅能保障数据稳定传输,提高网络吞吐率,还能降低节点能耗,延长网络的生存周期.
国内外在WSNs链路质量评估方面进行了大量的研究,主要包括基于物理层参数的评估、基于链路层参数的评估、综合性评估以及基于机器学习的评估.相比单一物理层参数或链路层参数的评估方法,综合性评估方法能更准确、更全面地评估链路质量[2].典型的综合性评估方法有基于模糊规则的链路质量评估方法[3]、基于模糊逻辑的链路质量综合评价指标[4]以及优化的基于模型规则链路评估方法[5]等.机器学习的方法越来越多地应用到链路质量评估中[6-7].
超限学习机(ELM, extreme learning machine)由Huang等提出,是一种随机权值的单隐层前馈神经网络学习算法,算法对参数设置要求低,模型简单,广泛应用于语种识别、图像识别等多分类问题[8].
笔者从链路的非对称性、波动性以及信道质量3个方面综合评估链路质量,借助ELM学习速度快、模型简单、分类精度较高的优势,采用粒子群优化算法(PSO, particle swarm optimization algorithm)优化ELM[9],构建基于PSO优化的ELM的链路质量评估模型(LQE-IELM, link quality estimation model based on improved extreme learning machine).
1 链路质量参数的选择考虑WSNs受环境噪声以及多径效应等因素的影响,链路质量呈现出波动性以及非对称性,通过上行和下行的均值信噪比(ASNR, average signal to noise ratio)差的绝对值来定义链路的非对称性指标(ASL, asymmetry level)[3],如
| $ \varphi = \left| {{{\bar \chi }_0} - {{\bar \chi }_1}} \right| $ | (1) |
其中:φ为ASL的值,χ0为上行ASNR,χ1为下行ASNR.
通过信噪比(SNR, signal to noise ratio)的变异系数(CV, coefficient of variation)[4]来度量波动性,如
| $ \gamma = \sigma \left( \chi \right)/\mu \left( \chi \right) $ | (2) |
其中:γ为CV的值,σ(χ)为SNR的方差,μ(χ)为SNR均值.通过ASNR来度量信道质量.
选择ASL、CV以及ASNR作为链路质量参数,选择包接收率(PRR, packet reception rate)来评价链路质量.
2 链路质量等级的划分用链路质量等级来描述链路质量状态,根据PRR将链路质量划分为5个等级,对应等级值为1~5,如表 1所示.
|
|
表 1 链路质量等级 |
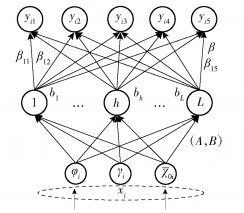
采用ELM构建链路质量评估模型,模型网络结构如图 1所示.
|
图 1 ELM链路质量评估模型结构 |
设初始样本集为T={(xi, yi)|(i=1, 2, …, N)},N为样本总数,xi=(φi, γi, χ0i)T为第i个样本对应的ASL、CV以及上行ASNR,yi=(yi1, yi2, yi3, yi4, yi5)为第i个样本的链路质量等级值one-hot编码.对于一个有L个隐含层节点的ELM网络, 有
| $ {o_i} = \sum\limits_{h = 1}^L {{\mathit{\boldsymbol{\beta }}_h}G\left( {{\mathit{\boldsymbol{a}}_h}{\mathit{\boldsymbol{x}}_i} + {b_h}} \right)} $ | (3) |
其中:oi=(oi1, oi2, oi3, oi4, oi5)为ELM在输出层上的输出;h为隐含层节点数;βh=(βh1, βh2, βh3, βh4, βh5)为第h个隐含层节点到输出节点的权重矩阵;ah为隐含层节点与输入层节点的权值矩阵,ah=(ρ1, ρ2, …, ρr, …, ρυ)T,其中ρr为第h个隐含层节点与第r个输入层节点的权重,υ为输入层节点个数,本文中为3;bh为第h个隐含层节点的偏置;G为激活函数,选用Sigmoid作为激活函数.
ELM训练的目标是使得期望输出与实际输出的误差最小,即
| $ \sum\limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{o}}_i} - {\mathit{\boldsymbol{y}}_i}} \right\| = 0} $ | (4) |
存在βh、ah、bh,使得
| $ {\mathit{\boldsymbol{y}}_i} = \sum\limits_{h = 1}^L {{\mathit{\boldsymbol{\beta }}_h}G\left( {{\mathit{\boldsymbol{a}}_h}{\mathit{\boldsymbol{x}}_i} + {b_h}} \right)} ,i = 1,2, \cdots ,N $ | (5) |
转换成矩阵形式,即
| $ \mathit{\boldsymbol{H\beta }} = \mathit{\boldsymbol{Y}} $ | (6) |
其中:H为隐含层节点的输出矩阵,
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {G\left( {{\mathit{\boldsymbol{a}}_1}{\mathit{\boldsymbol{x}}_1} + {b_1}} \right)}& \cdots &{G\left( {{\mathit{\boldsymbol{a}}_L}{\mathit{\boldsymbol{x}}_1} + {b_L}} \right)}\\ \vdots &{}& \vdots \\ {G\left( {{\mathit{\boldsymbol{a}}_1}{\mathit{\boldsymbol{x}}_N} + {b_1}} \right)}& \cdots &{G\left( {{\mathit{\boldsymbol{a}}_L}{\mathit{\boldsymbol{x}}_N} + {b_L}} \right)} \end{array}} \right] $ | (7) |
β为隐含层节点到输出层的权重矩阵,
| $ \mathit{\boldsymbol{\beta }} = {\left( {{\mathit{\boldsymbol{\beta }}_1},{\mathit{\boldsymbol{\beta }}_2}, \cdots ,{\mathit{\boldsymbol{\beta }}_L}} \right)^{\rm{T}}} $ | (8) |
Y为期望输出的链路质量等级编码矩阵,
| $ \mathit{\boldsymbol{Y}} = {\left( {{\mathit{\boldsymbol{y}}_1},{\mathit{\boldsymbol{y}}_2}, \cdots ,{\mathit{\boldsymbol{y}}_N}} \right)^{\rm{T}}} $ | (9) |
在ELM输入层权重与偏置参数随机确定后,隐含层节点的输出矩阵H得到确定,得到具有最小范数的唯一解
| $ \mathit{\boldsymbol{\hat \beta }} = {\mathit{\boldsymbol{H}}^ + }\mathit{\boldsymbol{Y}} $ | (10) |
其中:H+为H的Moore-Penrose广义逆,
将初始样本集按7: 3划分为训练集和测试集,隐含层节点数取经验值150,训练得到ELM链路质量评估的模型(LQE-ELM, link quality estimation model based on extreme learning machine).
3.2 评估模型参数的优化ELM中输入层权重矩阵A=(a1, a2, …, aL)和偏置参数矩阵B=(b1, b2, …, bL)是随机生成的,在隐含层节点数确定的情况下,其取值势必影响ELM评估模型的效果.采用PSO优化ELM模型参数A、B,得到LQE-IELM,
| $ V = {\rm{LQE}} - {\rm{IELM}}\left( {\mathit{\boldsymbol{A}},\mathit{\boldsymbol{B}},\mathit{\boldsymbol{\hat \beta }},G\left( x \right),L,\zeta } \right) $ | (11) |
其中:V为链路质量等级值,A的维度为L×υ,υ为输入层节点个数;B的维度为L×1;ζ为模型输入,ζ=(φ, γ, χ0).
PSO是一种模拟鸟群觅食的仿生优化算法,每个粒子都表示问题的一个解,具有实现容易、精度高、收敛快等优点[9].将ELM中A和B转换为Ψ×1的矩阵η,其中Ψ为
| $ \mathit{\Psi } = L\left( {\upsilon + 1} \right) $ | (12) |
定义粒子位置为η,粒子的速度定义为v,同样是Ψ×1的矩阵.
将ELM模型的链路质量评估准确率作为粒子的适应度,适应度值越大表示粒子位置越优.粒子通过式(13)更新自己的速度,利用式(14)更新自己的位置,得到评估准确率较高的ELM模型.
| $ \begin{array}{l} v_{kd}^{t + 1} = wv_{kd}^t + {c_1}\ell \left( {\hbar _{kd}^p - \eta _{kd}^t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{c_2}\ell \left( {\hbar _{kd}^g - \eta _{kd}^t} \right) \end{array} $ | (13) |
其中:vkdt+1、vkdt分别为第k个粒子在第t+1和t次迭代中第d维上的速度,d=1, 2, …, Ψ;
| $ \eta _{kd}^{t + 1} = \eta _{kd}^t + v_{kd}^{t + 1} $ | (14) |
其中ηkdt+1、ηkdt分别为第k个粒子在第t+1和t次迭代中的位置.
算法1
输入:最大迭代次数e,期望准确率τ,隐含层节点个数
输出:LQE-IELM.
步骤1 初始化参数,e=50,τ=0. 95,
步骤2 通过ELM评估模型输出得到初始粒子位置η,记录粒子
步骤3 粒子根据式(13)和式(14)更新自身速度和位置,结合
步骤4 若迭代次数大于e或模型准确率高于τ,则停止搜索,进入步骤5;若未达到最大迭代次数且准确率低于τ,则返回步骤3.
步骤5 输出LQE-IELM.
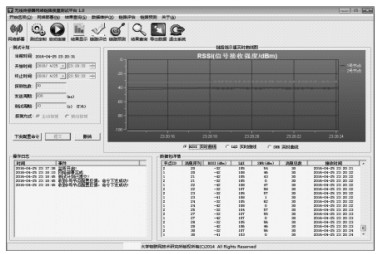
4 实验结果与分析采用美国CrossBow公司研制的TelosB节点和如图 2所示的南昌航空大学物联网技术研究所开发的链路质量测试平台在不同场景下获取链路质量信息.通过Matlab仿真平台实现LQE-IELM,并与ELM、支持向量分类机(SVC, support vector classification machine)[7]链路质量评估方法进行了对比实验.
|
图 2 链路质量测试平台 |
选择小树林、室内走廊、广场3个场景进行链路质量测试实验,构建星形网络,包括1个Sink节点和8个感知节点,如图 3所示.实验参数设置如表 2所示.

|
图 3 实验场景图 |
|
|
表 2 实验参数设置 |
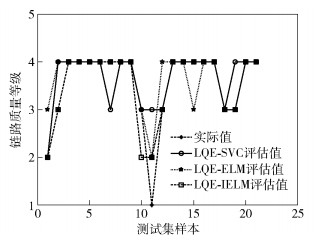
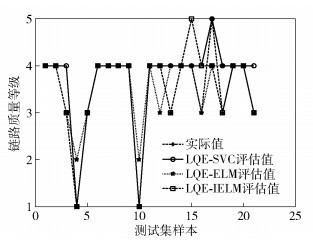
每个实验场景的实验数据都为3 373条,其中训练样本2 361条,测试样本1 012条,平均训练10次,随机抽取20个连续的测试样本,得到LQE-IELM的评估结果如图 4~图 6所示.图中实际值为链路质量测试样本的链路质量等级值,LQE-SVC评估值为采用基于k-折交叉验证算法优化的SVC方法[7]得到的链路质量评估等级值,LQE-ELM评估值为采用ELM方法得到的链路质量评估等级值,LQE-IELM评估值为采用LQE-IELM方法得到的链路质量评估等级值.
|
图 4 小树林场景评估结果 |
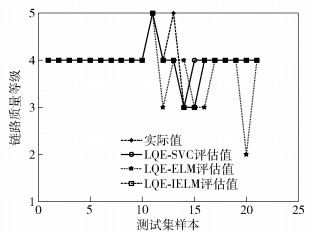
|
图 5 走廊场景评估结果 |
|
图 6 广场场景评估结果 |
由图 4~图 6可以看出,LQE-IELM评估值的分布与实际值分布基本吻合,LQE-ELM评估值与LQE-SVC评估值的分布与实际值吻合度不高.
3种方法在不同场景下的评估准确率见表 3.
|
|
表 3 不同场景下的评估准确率 |
由表 3可以看出,传统ELM链路质量评估方法与k-折交叉检验优化的SVC方法相比,评估准确率较低;所提出的LQE-IELM链路质量评估方法与传统ELM以及k-折交叉检验优化的SVC评估方法相比,具有更高的评估准确率.
5 结束语采用ELM的链路质量评估方法,选择ASL、CV、ASNR作为链路质量参数,可弥补单一链路质量参数的不足,以包接收率为链路质量评价指标,划分链路质量等级;采用PSO优化ELM输入层权重和偏置参数,构建基于粒子群优化的链路质量评估模型LQE-IELM. 3种场景下的实验结果表明,与SVC评估方法相比,所提出的方法具有较高的评估准确率.
| [1] |
刘洲洲, 王福豹. 能量有效的无线传感器网络无标度拓扑模型[J]. 北京邮电大学学报, 2015, 38(1): 87–91.
Liu Zhouzhou, Wang Fubao. Scale-free topology for wireless sensor networks with energy efficient characteristics[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(1): 87–91. |
| [2] | Baccour N, Koubâa A, Jamâa M B, et al. RadiaLE:a framework for designing and assessing link quality estimators in wireless sensor networks[J]. Ad Hoc Networks, 2011, 9(7): 1165–1185. doi: 10.1016/j.adhoc.2011.01.006 |
| [3] | Baccour N, Koubaa A, Youssef H, et al. Reliable link quality estimation in low-power wireless networks and its impact on tree-routing[J]. Ad Hoc Networks, 2015(27): 1–25. |
| [4] |
郭志强, 王沁, 万亚东, 等. 基于综合性评估的无线链路质量分类预测机制[J]. 计算机研究与发展, 2013, 50(6): 1227–1238.
Guo Zhiqiang, Wang Qin, Wan Yadong, et al. A classfication prediction mechanism based on comprehensive assessment for wireless link quality[J]. Journal of Computer Research and Development, 2013, 50(6): 1227–1238. doi: 10.7544/issn1000-1239.2013.20121299 |
| [5] | Rekik S, Baccour N, Jmaiel M, et al. Low-power link quality estimation in smart grid environments[C]//11th Wireless Communications and Mobile Computing Conference(IWCMC). Dubrovnik: IEEE Press, 2015: 1211-1216. |
| [6] | Liu Tao, Cerpa Alberto E. Foresee (4C): wireless link prediction using link features[C]//10th International Conference on Information Processing in Sensor Networks. Chicago: IEEE Press, 2011: 294-305. |
| [7] | Shu Jian, Liu Song, Liu Linlan, et al. Research on link quality estimation mechanism for wireless sensor networks based on support vector machine[J]. Chinese Journal of Electronics, 2017, 26(2): 377–384. doi: 10.1049/cje.2017.01.013 |
| [8] | Cao Jiuwen, Zhang Kai, Luo Minxia, et al. Extreme learning machine and adaptive sparse representation for image classification[J]. Neural Networks, 2016, 81(C): 91–102. |
| [9] | Yadav B, Ch S, Mathur S, et al. Estimation of in-situ bioremediation system cost using a hybrid extreme learning machine (ELM)-particle swarm optimization approach[J]. Journal of Hydrology, 2016(543): 373–385. |


