双线性多项式的非线性特征只能靠输入-输出交叉项表达,无法精确地表达高阶非线性系统.为此,对改进双线性多项式模型的稳定性进行了研究.利用迭代最小二乘法辨识改进双线性模型的参数,在复数域中,推导该算法的迭代公式,并验证了系统模型的稳定性.结果表明,通过迭代最小二乘法辨识得到的系统模型为有界输入-有界输出稳定.
The nonlinearity of bilinear polynomial only relies on the input-output cross term to express; it is hard to accurately describe the system with higher order nonlinearity. For improving the performance of models, many modified bilinear polynomials are proposed. However, the complex feedback terms cause models to be unstable, which restrict the modified models to be widely used in practice. Therefore, the stability of a modified bilinear model was analyzed. Recursive least squares (RLS) is used to identify parameters of the modified bilinear model, and the iterative formulas of the algorithm are deduced in the complex field. Simultaneously, the stability of the identified system is verified. It is shown that the bilinear system model identified by RLS, has bounded-input bounded-output stability.
在自适应非线性系统辨识中,Volterra级数是一种经典的数学模型.但在多数情况中,Volterra级数模型需要大量的系数来描述非线性系统,限制了它的实际应用.在这一情况下,许多改进的模型被相继提出,如维纳模型、汉默斯坦模型[1]、记忆多项式模型[2]、广义记忆多项式模型[3].双线性多项式也是其中之一,它将过去时刻的输出项和输入-输出交叉项引入一阶线性输入序列,是一种具有反馈结构的非线性模型[4].据文献[5-7]中的描述,双线性多项式模型能用较少的系数表现出比二阶Volterra级数模型更好的性能.但因为双线性模型只能依靠交叉项来表达非线性,当描述一个高阶非线性系统时,不能做到足够精确.为此,Zhao等[8]提出了改进的双线性模型,仿真实验结果表明,使用该模型和有限数量的系数可以以任意精度逼近大部分的非线性系统,但文中并没有在理论上对这个模型的稳定性进行具体分析.
众所周知,在反馈控制系统中,反馈回路能够大大改善系统的性能,但同时也可能引起系统的不稳定.这种现象在双线性多项式模型中同样存在,并且反馈项越复杂,多项式稳定性越难以保证. Lee等[9]在实数域中对传统双线性多项式模型的稳定性进行了分析,当输入信号满足特定激励条件时,模型的输出有界. Johnson等[10]对传统双线性多项式的一些重要类型稳定性的充分条件进行了总结.笔者针对文献[8]中提出的改进双线性多项式,在复数域中,验证它与迭代最小二乘法(RLS, recursive least squares)结合得到的系统模型的稳定性.
1 模型介绍传统双线性模型的表达式为
| $ \begin{array}{*{20}{c}} {y\left( n \right) = \sum\limits_{j = 1}^{{N_2} - 1} {{c_j}y\left( {n - j} \right)} + \sum\limits_{i = 0}^{{N_1} - 1} {{a_i}x\left( {n - i} \right)} + }\\ {\sum\limits_{i = 0}^{{N_1} - 1} {\sum\limits_{j = 1}^{{N_2} - 1} {{b_{i,j}}y\left( {n - j} \right)x\left( {n - i} \right)} } } \end{array} $ | (1) |
其中:x(n)和y(n)分别表示双线性系统的输入和输出信号,cj、bi, j和ai分别为输出项、交叉项和输入项的系数.第1部分由N2-1个时刻的输出信号线性构成,第2部分由N1个时刻的输入信号线性构成,第3部分由过去时刻输入-输出信息交叉构成.第1部分和第3部分即为反馈项.由于每时刻反馈和迭代的作用,这种模型能够比二阶Volterra级数模型以更少的系数而更有效地表达一个非线性系统.但由于双线性多项式模型是一个一维模型(一阶多项式只有纯粹的输入数据和输出数据,所以双线性多项式模型通常被称为一维模型,而不是一阶模型),其非线性特点只能依靠交叉项表达,对高阶非线性系统无法准确建模.
为了充分利用双线性多项式反馈的思路,拓宽其适用范围,文献[8]中对原始的双线性多项式模型做出适当的调整,改进后的双线性模型表达式为
| $ \begin{array}{*{20}{c}} {y\left( n \right) = \sum\limits_{i = 1}^{{Q_y}} {\sum\limits_{j = 1}^{{K_y}} {{a_{i,j}}y\left( {n - i} \right){{\left| {y\left( {n - i} \right)} \right|}^{j - 1}}} } + }\\ {\sum\limits_{i = 0}^{{Q_x}} {\sum\limits_{j = 1}^{{K_x}} {{b_{i,j}}x\left( {n - i} \right){{\left| {x\left( {n - i} \right)} \right|}^{j - 1}}} } } \end{array} $ | (2) |
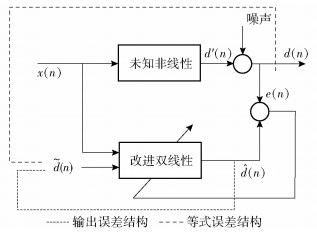
其中:ai, j和bi, j分别为反馈输出信号和输入信号的系数.对于模型中的参数,采用图 1所示的结构进行辨识.
|
图 1 输出误差结构和等式误差结构 |
根据图 1中的变量,对改进双线性多项式模型(式(2))重新表示为
| $ \begin{array}{*{20}{c}} {\hat d\left( n \right) = \sum\limits_{i = 1}^{{Q_d}} {\sum\limits_{j = 1}^{{K_d}} {{a_{i,j}}\tilde d\left( {n - i} \right){{\left| {\tilde d\left( {n - i} \right)} \right|}^{j - 1}}} } + }\\ {\sum\limits_{i = 0}^{{Q_x}} {\sum\limits_{j = 1}^{{K_x}} {{b_{i,j}}x\left( {n - i} \right){{\left| {x\left( {n - i} \right)} \right|}^{j - 1}}} } } \end{array} $ | (3) |
其中:x(n)和
常用的自适应辨识算法有迭代最小二乘法和最小均方算法(LMS, least mean squares).相对而言,LMS算法是最简单的一种自适应算法,其计算量小,但是收敛速度和收敛精度受到步长μ的限制,难以达到又快又好的效果.而RLS算法收敛速度和收敛精度都比LMS算法好,但是每次迭代的计算量都较大.综合考虑,采用RLS算法辨识改进双线性模型的参数.对于上文介绍的2种模型参数辨识结构,RLS辨识算法的推导过程相同.
为了便于推导,把式(3)记为如下矩阵形式:
| $ \hat d\left( n \right) = {\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{u}}\left( n \right) $ | (4) |
其中:a=[a1, 1, …, aQd, 1, …, aQd, Kd, b1, 1, …, bQx, Kx]T,代表系数向量,
对于N个采样时刻的数据,RLS的代价函数为
| $ J = \sum\limits_{n = 1}^N {e{{\left( n \right)}^2}} $ | (5) |
其中
| $ e\left( n \right) = d\left( n \right) - \hat d\left( n \right) = d\left( n \right) - {\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{u}}\left( n \right) $ | (6) |
为使式(5)达到极小值,对J求a的偏导,并令其等于零,即
| $ \begin{array}{*{20}{c}} {\nabla J = \frac{{\partial J}}{{\partial \mathit{\boldsymbol{a}}}} = - 2\sum\limits_{n = 1}^N {{\mathit{\boldsymbol{u}}^ * }\left( n \right)e\left( n \right)} = }\\ { - 2\sum\limits_{n = 1}^N {{\mathit{\boldsymbol{u}}^ * }\left( n \right)\left[ {d\left( n \right) - {\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{u}}\left( n \right)} \right]} = 0} \end{array} $ | (7) |
其中u*(n)是u(n)的共轭矩阵,所以
| $ \sum\limits_{n = 1}^N {{\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right)} = \sum\limits_{n = 1}^N {{\mathit{\boldsymbol{u}}^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{a}}} $ | (8) |
可将式(8)写为
| $ {\mathit{\boldsymbol{U}}^{\rm{H}}}\left( N \right)\mathit{\boldsymbol{D}}\left( N \right) = {\mathit{\boldsymbol{U}}^{\rm{H}}}\left( N \right)\mathit{\boldsymbol{U}}\left( N \right)\mathit{\boldsymbol{a}} $ | (9) |
其中
| $ \mathit{\boldsymbol{U}}\left( N \right) = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}\left( 1 \right)}&{\mathit{\boldsymbol{u}}\left( 2 \right)}& \cdots &{\mathit{\boldsymbol{u}}\left( N \right)} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{D}}\left( N \right) = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{d}}\left( 1 \right)}&{\mathit{\boldsymbol{d}}\left( 2 \right)}& \cdots &{\mathit{\boldsymbol{d}}\left( N \right)} \end{array}} \right]^{\rm{T}}} $ |
所以
| $ \mathit{\boldsymbol{a}} = {\left[ {{\mathit{\boldsymbol{U}}^{\rm{H}}}\left( N \right)\mathit{\boldsymbol{U}}\left( N \right)} \right]^{ - 1}}{\mathit{\boldsymbol{U}}^{\rm{H}}}\left( N \right)\mathit{\boldsymbol{D}}\left( N \right) $ | (10) |
定义
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( N \right) = {\mathit{\boldsymbol{U}}^{\rm{H}}}\left( N \right)\mathit{\boldsymbol{U}}\left( N \right) = \sum\limits_{n = 1}^N {{\mathit{\boldsymbol{u}}^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)} $ |
| $ \mathit{\boldsymbol{P}}\left( N \right) = {\mathit{\boldsymbol{U}}^{\rm{H}}}\left( N \right)\mathit{\boldsymbol{D}}\left( N \right) = \sum\limits_{n = 1}^N {{\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right)} $ |
从而可以将式(10)表示为
| $ \mathit{\boldsymbol{a}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( N \right)\mathit{\boldsymbol{P}}\left( N \right) $ | (11) |
从Φ(N)和P(N)的定义中还能得出
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( n \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {n - 1} \right) + {\mathit{\boldsymbol{u}}^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right) $ | (12) |
| $ \mathit{\boldsymbol{P}}\left( n \right) = \mathit{\boldsymbol{P}}\left( {n - 1} \right) + {\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right) $ | (13) |
为了求Φ(N)的逆矩阵,引入矩阵求逆引理:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{ - 1}} = {{\left( {\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{CDE}}} \right)}^{ - 1}} = }\\ {{\mathit{\boldsymbol{B}}^{ - 1}} - {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{C}}{{\left( {{\mathit{\boldsymbol{D}}^{ - 1}} + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{C}}} \right)}^{ - 1}}\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{B}}^{ - 1}}} \end{array} $ | (14) |
对应到式(13)上,令A=Φ(n),B=Φ(n-1),C=u*(n),D=1,E=uT(n),所以Φ-1(n)为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( n \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( {n - 1} \right) - }\\ {\frac{{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( {n - 1} \right)}}{{1 + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)}}} \end{array} $ | (15) |
令
| $ \mathit{\boldsymbol{C}}\left( n \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( n \right) $ | (16) |
| $ \mathit{\boldsymbol{g}}\left( n \right) = \frac{{\mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)}}{{1 + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)}} $ | (17) |
则式(15)可写为
| $ \mathit{\boldsymbol{C}}\left( n \right) = \mathit{\boldsymbol{C}}\left( {n - 1} \right) - \mathit{\boldsymbol{g}}\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( {n - 1} \right) $ | (18) |
同时,从式(17)可以推出
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{g}}\left( n \right) = \mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right) - }\\ {\mathit{\boldsymbol{g}}\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right) = }\\ {\mathit{\boldsymbol{C}}\left( n \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)} \end{array} $ | (19) |
根据式(11)和式(13),再结合式(18)、式(19),能够得到
| $ \begin{array}{*{20}{c}} {\vec a\left( n \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\left( n \right)\mathit{\boldsymbol{P}}\left( n \right) = }\\ {\mathit{\boldsymbol{C}}\left( n \right)\left[ {\mathit{\boldsymbol{P}}\left( {n - 1} \right) + {\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right)} \right] = }\\ {\mathit{\boldsymbol{C}}\left( {n - 1} \right)\mathit{\boldsymbol{P}}\left( {n - 1} \right) - g\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right) \times }\\ {\mathit{\boldsymbol{C}}\left( {n - 1} \right)\mathit{\boldsymbol{P}}\left( {n - 1} \right) + \mathit{\boldsymbol{g}}\left( n \right)d\left( n \right) = }\\ {\mathit{\boldsymbol{a}}\left( {n - 1} \right) + \mathit{\boldsymbol{g}}\left( n \right)\left[ {d\left( n \right) - {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{a}}\left( {n - 1} \right)} \right]} \end{array} $ | (20) |
a(n)为第n次迭代时的系数向量,令α(n)为先验估计误差[11]:
| $ \alpha \left( n \right) = d\left( n \right) - {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{a}}\left( {n - 1} \right) $ | (21) |
所以,式(20)又可写为
| $ \mathit{\boldsymbol{a}}\left( n \right) = \mathit{\boldsymbol{a}}\left( {n - 1} \right) + \mathit{\boldsymbol{g}}\left( n \right)\alpha \left( n \right) $ | (22) |
综上可得RLS的迭代公式:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}\left( n \right) = \mathit{\boldsymbol{a}}\left( {n - 1} \right) + \mathit{\boldsymbol{g}}\left( n \right)\alpha \left( n \right)}\\ {\mathit{\boldsymbol{g}}\left( n \right) = \frac{{\mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)}}{{1 + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)}}}\\ {\mathit{\boldsymbol{C}}\left( n \right) = \mathit{\boldsymbol{C}}\left( {n - 1} \right) - \mathit{\boldsymbol{g}}\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( {n - 1} \right)} \end{array} $ | (23) |
对基于改进双线性多项式与RLS算法得到的系统模型稳定性进行了证明,具体过程如下.
根据式(6)和式(21)有以下推导:
| $ \begin{array}{*{20}{c}} {\alpha \left( n \right) = e\left( n \right) + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{a}}\left( n \right) - {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{a}}\left( {n - 1} \right) = }\\ {e\left( n \right) + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\left[ {\mathit{\boldsymbol{a}}\left( n \right) - \mathit{\boldsymbol{a}}\left( {n - 1} \right)} \right]} \end{array} $ | (24) |
结合式(22),得到
| $ \begin{array}{*{20}{c}} {\alpha \left( n \right) = e\left( n \right) + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{g}}\left( n \right)\alpha \left( n \right)}\\ {e\left( n \right) = \left[ {1 - {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{g}}\left( n \right)} \right]\alpha \left( n \right)} \end{array} $ | (25) |
将式(17)代入式(25),e(n)与α(n)可变为
| $ \begin{array}{*{20}{c}} {e\left( n \right) = \frac{{\alpha \left( n \right)}}{{1 + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)}}}\\ {\alpha \left( n \right) = \left[ {1 + {\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)} \right]e\left( n \right)} \end{array} $ | (26) |
再利用式(13)和式(22),可以推出
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( n \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( n \right)\mathit{\boldsymbol{a}}\left( n \right) = {\mathit{\boldsymbol{a}}^{\rm{H}}}\left( n \right)\mathit{\boldsymbol{P}}\left( n \right) = }\\ {{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {n - 1} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {n - 1} \right)\mathit{\boldsymbol{a}}\left( {n - 1} \right) + }\\ {{\alpha ^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( n \right)\mathit{\boldsymbol{P}}\left( {n - 1} \right) + }\\ {{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right) + }\\ {{\alpha ^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( n \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right)} \end{array} $ | (27) |
其中,根据式(11)、式(13),有
| $ \begin{array}{*{20}{c}} {{\alpha ^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( n \right)\mathit{\boldsymbol{P}}\left( {n - 1} \right) + }\\ {{\alpha ^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{C}}\left( n \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right) = }\\ {{\alpha ^ * }\left( n \right){\mathit{\boldsymbol{u}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{a}}\left( n \right) = {\alpha ^ * }\left( n \right)\left[ {d\left( n \right) - e\left( n \right)} \right]} \end{array} $ | (28) |
根据式(21),得
| $ {\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {n - 1} \right){\mathit{\boldsymbol{u}}^ * }\left( n \right)d\left( n \right) = \left[ {{d^ * }\left( n \right) - {\alpha ^ * }\left( n \right)} \right]d\left( n \right) $ | (29) |
结合式(28)、式(29),式(27)有如下形式:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( n \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( n \right)\mathit{\boldsymbol{a}}\left( n \right) = }\\ {{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {n - 1} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {n - 1} \right)\mathit{\boldsymbol{a}}\left( {n - 1} \right) + }\\ {{{\left| {d\left( n \right)} \right|}^2} - e\left( n \right){\alpha ^ * }\left( n \right) = }\\ {{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {n - 1} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {n - 1} \right)\mathit{\boldsymbol{a}}\left( {n - 1} \right) + {{\left| {d\left( n \right)} \right|}^2} - }\\ {e\left( n \right){e^ * }\left( n \right)\left[ {1 + {\mathit{\boldsymbol{u}}^{\rm{H}}}\left( n \right){\mathit{\boldsymbol{C}}^ * }\left( {n - 1} \right)\mathit{\boldsymbol{u}}\left( n \right)} \right]} \end{array} $ |
即
| $ \begin{array}{*{20}{c}} {{{\left| {e\left( n \right)} \right|}^2}\left[ {1 + {\mathit{\boldsymbol{u}}^{\rm{H}}}\left( n \right){\mathit{\boldsymbol{C}}^ * }\left( {n - 1} \right)\mathit{\boldsymbol{u}}\left( n \right)} \right] = }\\ {{{\left| {d\left( n \right)} \right|}^2} + {\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {n - 1} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {n - 1} \right)\mathit{\boldsymbol{a}}\left( {n - 1} \right) - }\\ {{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( n \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( n \right)\mathit{\boldsymbol{a}}\left( n \right)} \end{array} $ | (30) |
将等式(30)两边从n=1累加到n=N,并除以N+1,得
| $ \begin{array}{*{20}{c}} {\frac{1}{{N + 1}}\sum\limits_{n = 1}^N {\left\{ {{{\left| {e\left( n \right)} \right|}^2}\left[ {1 + {\mathit{\boldsymbol{u}}^{\rm{H}}}\left( n \right) \times } \right.} \right.} }\\ {\left. {{\mathit{\boldsymbol{C}}^ * }\left( {n - 1} \right)\mathit{\boldsymbol{u}}\left( n \right)} \right\} = }\\ {\frac{1}{{N + 1}}\sum\limits_{n = 1}^N {{{\left| {d\left( n \right)} \right|}^2}} + \frac{1}{{N + 1}}{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( { - 1} \right) \times }\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( { - 1} \right)\mathit{\boldsymbol{a}}\left( { - 1} \right) - \frac{1}{{N + 1}}{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( N \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( N \right)\mathit{\boldsymbol{a}}\left( N \right)} \end{array} $ |
因为Φ(N)为正定矩阵,所以
| $ \begin{array}{*{20}{c}} {\frac{1}{{N + 1}}\sum\limits_{n = 1}^N {{{\left| {e\left( n \right)} \right|}^2}} < }\\ {\frac{1}{{N + 1}}\sum\limits_{n = 1}^N {\left\{ {{{\left| {e\left( n \right)} \right|}^2}\left[ {1 + {\mathit{\boldsymbol{u}}^{\rm{H}}}\left( n \right) \times } \right.} \right.} }\\ {\left. {\left. {{\mathit{\boldsymbol{C}}^ * }\left( {n - 1} \right)\mathit{\boldsymbol{u}}\left( n \right)} \right]} \right\} < }\\ {\frac{1}{{N + 1}}\sum\limits_{n = 1}^N {{{\left| {d\left( n \right)} \right|}^2}} + \frac{1}{{N + 1}}{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( { - 1} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( { - 1} \right)\mathit{\boldsymbol{a}}\left( { - 1} \right)} \end{array} $ |
因为d(n)是未知系统的实际输出,所以其均方值必定有界,进而可以推出e(n)的均方值也是有界的.根据e(n)的定义(式(6)),能够得出改进双线性模型时刻n的实际输出
对基于RLS算法的改进双线性多项式模型进行分析研究,推导了双线性多项式模型的迭代公式,验证了该系统模型具有有界输入-有界输出的稳定性.这一模型不仅可以用于自适应非线性系统辨识,还可被广泛用于线性化预处理[11]、声音信号预测、非线性信道均衡[6]、有源噪声控制[7]等领域.
| [1] | Nordsjo A, Zetterberg L. Identification of certain time-varying nonlinear Wiener and Hammerstein systems[J]. IEEE Trans Signal Process, 2001, 49(3): 577–592. doi: 10.1109/78.905884 |
| [2] | Ding L, Zhou G T, Morgan D R, et al. A robust digital baseband predistorter constructed using memory polynomials[J]. IEEE Trans Commun, 2004, 52(1): 159–165. doi: 10.1109/TCOMM.2003.822188 |
| [3] | Dennis R, Ma Zhengxiang, Kim Jaehyeong, et al. A generalized memory polynomial model for digital predistortion of RF power amplifiers[J]. IEEE Trans Signal Process, 2006, 54(10): 3852–3860. doi: 10.1109/TSP.2006.879264 |
| [4] | Diniz P S R. Adaptive filtering algorithms and practical implementation[M]. Boston: Springer, 2008: 191-193. |
| [5] | Baik Heung Ki, Mathews V John. Adaptive lattice bilinear filters[J]. IEEE Transactions on Signal Process, 1993, 41(6): 2033–2046. doi: 10.1109/78.218134 |
| [6] | Zhang Jiashu, Zhao Haiquan. A novel adaptive bilinear filter based on pipelined architecture[J]. Digital Signal Process, 2010, 20(1): 23–38. doi: 10.1016/j.dsp.2009.06.006 |
| [7] | Kuo Sen M, Wu Hsien-Tsai. Nonlinear adaptive bilinear filters for active noise control systems[J]. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2005, 52(3): 617–624. doi: 10.1109/TCSI.2004.842429 |
| [8] | Zhao Xia, Li Zhanning. A modified bilinear polynomial model for digital predistortion of RF power amplifiers[J]. Chinese Automation Congress (CAC), 2015: 91–95. |
| [9] | Lee Junghsi, Mathews V John. A stability result for RLS adaptive bilinear filters[J]. IEEE Signal Processing Letters, 1994, 1(12): 191–193. doi: 10.1109/97.338749 |
| [10] | Johnson Kelly K, Sandberg Irwin W. Notes on the stability of bilinear filters[J]. IEEE Transactions on Signal Process, 1998, 46(7): 2056–2058. doi: 10.1109/78.700983 |
| [11] | Tokunbo Ogunfunmi. Adaptive nonlinear system identification[M]. Boston: Springer, 2007: 95-96. |
| [12] | Mumolo E, Carini A. On the stability of discrete time recursive Volterra filters[J]. IEEE Signal Processing Letters, 1999, 6(9): 230–232. doi: 10.1109/97.782067 |


