2. 温州市铁路与轨道交通投资集团有限公司, 浙江 温州 325000
提出了一种新型的曲面射线管应用于射线追踪中的绕射射线路径预测.相比于现有的四边形波前面绕射射线管,曲面射线管能够在追踪的过程中有效地减少计算时间,提高追踪效率.通过理论分析推导,证明该模型相比于四边形射线管,在采用的追踪实例中计算效率提高了约4倍.详细介绍了特殊凹陷地形与射线管求交的处理情况.通过基于四边形波前面射线管和曲面射线管的不同算法计算,对追踪时间和结果进行了对比,曲面射线管的平均计算时间缩短了约18.49%,平均误差仅为2.93%,效率得到了提高,也验证了追踪结果路径的准确性.
2. Wenzhou Mass Transit Railway Investment Group Co., Ltd., Zhejiang Wenzhou 325000, China
A ray tracing method for predicting radio propagation based on a new curved surface ray tube was presented. Compared with the existing quadrilateral wave front diffraction ray tube, the curved surface ray tube can effectively reduce the calculation time and improve the efficiency during the tracing process. Calculation verified the high efficiency of the curved surface ray tube model, a 4 times speed up compared to the four-ray tube model was achieved. The method to deal with the intersection of the ray tube and the concave terrain was also introduced. Moreover, the wave propagations in several different environments were simulated with our developed software based on the curved surface ray tube and four-ray tube tracing method. Compared with the four-ray tube model, the average computational time of the cured surface ray tube model is shortened by about 18.49%, and the average error is only 2.93%. The simulation results prove the improvement of the efficiency and the accuracy of the tracing process.
近年来,射线追踪算法不断成熟和发展,并应用于电磁环境仿真的研究.一致性绕射理论也与射线追踪算法相结合[1-3].射线追踪算法中,反向算法具有较高的精度,但其消耗较多的计算时间.现阶段广泛应用于电磁仿真中的射线追踪算法为计算速度快的射线弹跳算法[4-11].
在射线弹跳法的应用过程中,提出了多种追踪模型.中心射线管[2]可以抽象为圆锥形射线管,用射线管内中心射线来预测其余射线的传播路径.由于圆锥形中心射线管的波前面为圆形或椭圆形,波前面在覆盖整个空间时会出现重叠,造成路径重复.侧面射线管模型[2-6]很好地解决了中心射线管的重叠问题,其中正二十面体发射模型[4-5]和四边形射线管发射模型[2-3, 6]都能使所发射的射线管的波前面无缝无重叠地覆盖整个空间区域,避免了射线遗漏和重复.为预测绕射射线的传播,结合一致性绕射理论的四边形波前面射线管模型[2-3]可应用于射线追踪中,解决点发射射线管无法追踪绕射射线的问题.基于上述射线管,Bernardi等[7]提出了一种三角形波前面射线管,但没有描述该模型的产生方式及具体特征以及应用在射线追踪中的详细过程.现有的射线管进行射线追踪获得反射射线管的方法[7-8]无法直接处理射线管与凹陷地形相交的情况.
笔者在上述基础上,定义了一种由棱发射的曲面射线管.这种新绕射射线管相比于传统四边形波前面射线管,能够更高效地处理与地形面求交的情况.它没有四边形波前面射线管在与地形求反射过程中为保持固有特性而补全射线管这一过程,因此能在不造成冗余的情况下,达到相同的准确追踪效果.笔者针对射线管与凹陷地形求反射的情况,提出了相应的算法,并进行了详细分析,通过仿真验证了其结果的正确性.
1 曲面射线管模型现阶段应用于射线追踪算法中绕射射线追踪的模型,主要为棱发射四边形波前面原始射线管[2-3, 6](见图 1).确定原始射线管的4条射线分别从同一条棱上的不同两点发出,由同一点发出的2条射线及不同点发出的相邻2条射线分别共面.因此这种射线管符合传统射线管的定义,即射线管的侧面为平面.曲面射线管(见图 1)是将原始射线管的四边形波前划分而形成的2个波前为三角形的射线管.对于波前面为CDE的曲面射线管,确定射线管的3条射线AC、AE和BD中,AE和BD 2条射线异面,因此ABDE为由棱发出的异面射线构成的曲面.

|
图 1 棱发射原始射线管模型生成曲面射线管 |
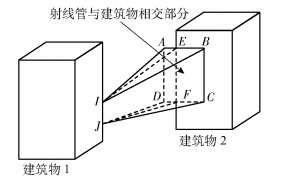
原始射线管在用于求建筑物反射和绕射(见图 2)时具有高效性和实用性.将建筑物抽象成为长方体,建筑物的棱都为平行或者垂直关系,因此建筑物1的棱IJ产生的射线管在与建筑物2的一个侧面部分相交时,可根据相交情况将射线管的波前面分为AEFD和BCFE 2个部分,分别构建新的射线管.其中,波前面为BCFE的射线管在建筑物2的侧面上发生反射,而波前面为ADFE的射线管则独立地继续进行追踪.
|
图 2 棱发射原始射线管应用于城市环境追踪 |
当原始射线管应用于复杂不规律地形求反射绕射时,会造成冗余.假设地形是由三角面组成的,则射线管与地形求交即可抽象为射线管与三角面求交.由于地形的复杂多样,生成的绕射射线管角度不确定,因此其与地形求交的情况也存在着多样性.如果射线管波前面与地形三角面相交部分不规则,则需要通过补全方法构造下一步的射线管,但补全的过程就会造成下一步需要追踪射线数量的增加,产生冗余.
如图 3所示,发射棱生成的原始射线管与地形三角面相交的部分为波前面GHIJ上的阴影部分.将发射棱相对于地形三角面做镜像,得到虚拟发射棱AB,由虚拟发射棱产生的对应射线管的传播方向,即为原始射线管反射后的传播方向.由于反射区域(波前面GHIJ上的阴影部分)无法作为一个原始射线管的波前面,所以需要对其进行补全,补全部分即为波前面GHIJ上的非阴影部分.

|
图 3 原始射线管反射后与地形面相交 |
定义图 3中的各项参数:OA=K1,OB=K2,AC=L11,AD=L12,BE=L21,BF=L22,AB=W,∠AOB=θ,∠CAD=∠EBF=α.用z表示CF的长度,根据几何计算可以将z表示为
| $ z = \sqrt {x_4^2 + {x_1}{x_2} + \frac{{{x_2}\left( {x_3^2 - x_2^2} \right)}}{{{x_2} - {x_1}}}} $ | (1) |
其中
| $ \left. \begin{array}{l} {x_1} = \frac{{W\left( {{L_{11}} + {K_1}} \right)}}{{{K_1}}}\\ {x_2} = \frac{{W\left( {{L_{22}} + {K_2}} \right)}}{{{K_2}}}\\ {x_3} = \sqrt {\frac{{K_2^2L_{22}^2}}{{K_2^2}} + L_{22}^2 - \frac{{2K_2^{}L_{11}^{}{L_{22}}}}{{{K_1}}}\cos \alpha } \\ {x_4} = \sqrt {\frac{{K_1^2L_{22}^2}}{{K_2^2}} + L_{11}^2 - \frac{{2K_1^{}L_{11}^{}{L_{22}}}}{{{K_2}}}\cos \alpha } \end{array} \right\} $ | (2) |
假定四边形CDFE的边长分别表示为CD=y1,DF=y2,EF=y3,CE=y4,则有
| $ \left. \begin{array}{l} {y_1} = \sqrt {L_{11}^2 + L_{12}^2 - 2{L_{11}}{L_{22}}\cos \alpha } \\ {y_2} = \sqrt {{{\left( {{L_{12}} + {K_1}} \right)}^2} + {{\left( {{L_{22}} + {K_2}} \right)}^2} - 2\left( {{L_{12}} + {K_1}} \right)\left( {{L_{22}} + {K_2}} \right)\cos \theta } \\ {y_3} = \sqrt {L_{21}^2 + L_{22}^2 - 2{L_{21}}{L_{22}}\cos \alpha } \\ {y_4} = \sqrt {{{\left( {{L_{11}} + {K_1}} \right)}^2} + {{\left( {{L_{21}} + {K_2}} \right)}^2} - 2\left( {{L_{11}} + {K_1}} \right)\left( {{L_{21}} + {K_2}} \right)\cos \theta } \end{array} \right\} $ | (3) |
波前面CDFE的面积用Sf表示,则
| $ \begin{array}{l} {S_{\rm{f}}} = \sqrt {{p_1}\left( {{p_1} - {y_1}} \right)\left( {{p_1} - {y_2}} \right)\left( {{p_1} - z} \right)} + \\ \;\;\;\;\;\;\;\sqrt {{p_2}\left( {{p_2} - {y_3}} \right)\left( {{p_2} - {y_4}} \right)\left( {{p_2} - z} \right)} \end{array} $ | (4) |
其中
| $ \left. \begin{array}{l} {p_1} = \frac{1}{2}\left( {{y_1} + {y_2} + z} \right)\\ {p_2} = \frac{1}{2}\left( {{y_3} + {y_4} + z} \right) \end{array} \right\} $ | (5) |
补全射线管会使其波前面增大.现有的射线追踪算法以地形三角面作为计算单位,当波前面包含多个地形三角面时,相交情况会十分复杂,无法处理,此时需要将射线管细分为多个小的射线管.细分过程造成射线管个数的增加,由于追踪时间与射线管个数成正比,追踪时间将成倍增加,对后续的追踪造成负担.
若地形三角面的面积为a,当相交部分的面积大于a时便需要细分.假设一个射线管被细分为c个新的射线管,细分时间为t1,求交的时间为t2,因此射线管经过反射后与地形面求交的时间Tf可以表示为
| $ {T_{\rm{f}}} = \left\lceil {\frac{{\ln \left\lceil {\frac{{{S_{\rm{f}}}}}{a}} \right\rceil }}{{\ln c}}} \right\rceil {t_1} + \left\lceil {\frac{{{S_{\rm{f}}}}}{a}} \right\rceil {t_2} $ | (6) |
若阴影部分占波前面的比例为r,原始射线管在发生反射后采用了补全的方法,则下一次与地形面求交时会产生冗余.
笔者所提出的曲面射线可以很好地解决以上问题.确定曲面射线管的相邻2条射线可以是异面射线,形成射线管的侧面为曲面.形成曲面射线管的条件为,射线管中所有射线都是由一个源点发射后通过同一条绕射棱产生的.笔者主要介绍一种由3条射线确定,波前面为三角形的曲线射线管(见图 1),以下所提到的曲面射线管都为这种射线管.
由于绕射射线管是由发射机产生的射线或反射射线经棱绕射形成的,曲面射线管中的所有射线都具有一个公共的虚拟发射点.结合几何光学绕射理论,绕射棱产生的所有绕射射线在传播过程中互不相交,不会有射线穿出曲面.曲面射线管对于内部的射线是封闭的,可覆盖整个空间,因此可用于绕射射线追踪.
对于确定曲面射线管的3条射线来说,没有严格规定其相邻2条射线是在同一个平面上的.当曲面射线管与地形三角面相交时,相交部分总可以划分为一个或多个三角形波前面,构造新的曲面射线管进行后续追踪,因此不存在补全的冗余.如果将曲面射线管应用于图 3的情境中,则只有阴影部分会产生反射射线管,所以反射射线管波前面与地形面相交的部分面积SCSRT为
| $ {S_{{\rm{CSRT}}}} = r{S_{\rm{f}}} $ | (7) |
利用曲面射线管计算使用的时间TCSRT表示为
| $ {T_{{\rm{CSRT}}}} = \left\lceil {\frac{{\ln \left\lceil {\frac{{{S_{{\rm{CSRT}}}}}}{a}} \right\rceil }}{{\ln c}}} \right\rceil {t_1} + \left\lceil {\frac{{{S_{{\rm{CSRT}}}}}}{a}} \right\rceil {t_2} $ | (8) |
因此,利用原始射线管进行追踪和利用曲面射线管进行追踪耗费的时间比,即曲面射线管相对于原始射线管的效率:
| $ \eta = \frac{{{T_{\rm{f}}}}}{{{T_{{\rm{CSRT}}}}}} $ | (9) |
若式(1)~式(8)中,K1=K2=10 m,L11=L21=10 000 m,L12=L22=1 000 m,W=10 m,θ=π/3,α=π/6,r=1/4,a=100 m2,c=4.通过计算可得Tf=10t1+438 831t2,TCSRT=9t1+109 708t2.由于相比于t2,t1的值非常小可以忽略,可以计算得到η≈4.因此在图 3所示的场景下,曲面射线管相对于原始射线管将计算效率提高了大约4倍,证明其能够更加高效地处理复杂地形面中的射线追踪问题.
2 射线管与特殊地形求交处理方法在射线追踪的过程中,求反射路径是最基本的操作,占据计算过程的绝大部分,因此保证反射路径的求解正确性至关重要.
2.1 射线管与特殊地形相交出现的问题射线管以有限数量的射线为边界,确定一个射线束的范围.这种追踪方法能够覆盖整个传播空间,因此比单条射线追踪在精度上有很大的提升.但是在一个射线管中只有边界射线是已知的,因此需通过对于已知射线的追踪来判断内部射线的传播情况.当射线管与相对平坦的地形相交时,内部射线的传播情况与已知射线基本一致.但当出现明显凹陷的特殊地形时,可能出现边界射线与内部射线传播不一致的情况.
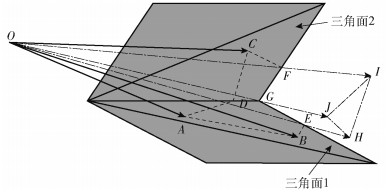
如图 4所示的凹陷地形,当一个射线管的3条边界射线(OA、OB和OC)与2个相邻的地形面相交时,如果射线管内部射线与这3条射线的传播情况一致,则内部射线也应与这2个地形面相交.但根据图 4中射线管传播方向可以明显观察到,射线管中有部分射线未与地形面相交且继续向前传播.这时内部射线与边界射线管传播情况一致的处理方法会造成射线的遗漏.为避免这种现象的发生,须对其进行特殊处理.
|
图 4 射线管与特殊地形面相交的情况 |
由于内部射线与地形作用的情况未知,所以需要先确定射线管的边界与地形发生相交的部分. 图 4所示的3条已知射线中OA和OB与三角面1相交,OC与三角面2相交,因此由射线OA和OB构成的面与三角面1的交线即为交点的连线AB.射线管侧面OAC与三角面1和三角面2的交线分别为AD和CD,2条交线相交于D点,因此该侧面上的射线与地形面的交点均在2个三角面内.面OBC与三角面1和三角面2的交线分别为线段BE和CF,由于E、F两点不重合,则OBC上有部分射线与两三角面不相交.
由于射线管具有封闭性,可以确定未与地形三角面1和三角面2相交射线束的边界为点E、F、G所对应的射线.为了能够继续追踪未相交射线的传播情况,分别连接OE、OF、OG构成3条射线,并由这3条射线构成一个新的波前面为HIJ的射线管,继续进行追踪.相交部分则构建反射射线管.
3 仿真结果验证笔者分别使用以原始射线管和曲面射线管为绕射模型建立的仿真系统,对相同的地形进行仿真.曲面射线管仿真系统使用了第2节所介绍的求交方法.通过比较2个仿真系统对于同一地形的仿真结果、路径、场强及仿真时间来验证曲面射线管的效率以及射线管与特殊地形求交处理方式的准确性.仿真所使用地形的系数均为εr=25,σ=0.02.
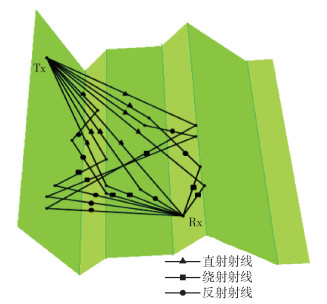
图 5所示为大小是560 m×750 m的地形,地形中的绕射棱均平行.地形中分别设置了一个发射机(Tx(17.86, 576.55, 223.46))和一个接收机(Rx(330.89, 269.15, 172.70)),发射机与接收机之间的距离为441.65 m.通过基于原始射线管和曲面射线管建立的仿真系统分别对该地形上由Tx发射被Rx接收的射线路径进行仿真,在不考虑发射机和接收机与地面之间距离的情况下,仿真得到的路径均为6条(见图 5),证明了曲面射线管在预测射线传播路径时,具有与原始射线管相同的准确性.
|
图 5 仅具有平行绕射棱的简单地形 |
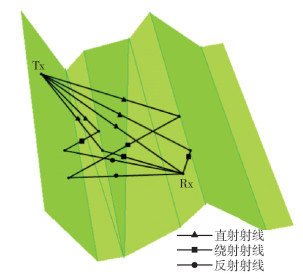
图 6所示的地形与图 5所示的地形具有相同的大小和位于相同位置的发射机和接收机,但其将地形中的一条绕射棱进行了旋转,使得2条棱不再平行.通过采用2种不同模型的仿真系统进行仿真,仍可得到相同的5条传播路径(见图 6).对于图 5和图 6中2种仿真系统结果的对比,也证明了所提出的特殊地形求交处理方法能够正确地处理特殊相交情况,得到正确的预测结果.
|
图 6 具有不平行绕射棱的简单地形 |
表 1为使用曲面射线管模型和原始射线管模型对应的仿真系统分别进行仿真后,接收机处的计算时间和场强大小对比,计算频率为1 GHz. 表 1中的相交面积为追踪过程中射线管波前面与地形相交面积的总和.地形3(42°19'26.60"N 82°50'25.81"E~42°18'25.78"N 82°52'4.75"E)的大小为2 km×2.2 km,发射机和接收机之间的距离为609.63 m.地形4(42°21'31.61"N 82°48'28.35"E~42°16'44.17"N 82°55'40.76"E)的大小为9.5 km×10 km,发射机和接收机之间的距离为439.60 m.
|
|
表 1 2种模型计算时间和场强对比 |
表 1所示的地形按照地形1~地形4的顺序,复杂度不断增加.由结果可知,当用于简单地形的追踪时,曲面射线管和原始射线管的追踪时间相差不大.但当应用于复杂地形时,曲面射线管比原始射线管消耗更少的计算时间.同时,表 1示出了由2种不同模型仿真后接收机接收到场强的误差,平均误差仅为2.93%,证明了曲面射线管和特殊地形求交算法的准确性.
4 结束语介绍了一种由3条射线确定的、应用于绕射射线追踪的曲面射线管模型,与棱发射四边形波前面射线管模型相比,在处理复杂地形时的效率上有明显的提高.同时,还对射线管作用于凹陷地形的处理方式进行了详细分析,并验证了其准确性.所提出的方法和模型能够有效应用于复杂地形环境中的射线追踪仿真,并能快速、准确地对射线传播路径和场强进行预测和计算,在实际中能应用于电波传播预测、无线网络覆盖分析和复杂电磁环境仿真.
| [1] | Son Hae-Won, Myung Noh-Hoon. A deterministic ray tube method for microcellular wave propagation prediction model[J]. IEEE Trans Antennas Propagat, 1999, 47(8): 1344–1350. doi: 10.1109/8.791954 |
| [2] | Saeidi Chiya, Fard Azim, Hodjatkashani Farrokh. Full three-dimensional radio wave propagation prediction model[J]. IEEE Trans Antennas Propagat, 2012, 60(5): 2462–2471. doi: 10.1109/TAP.2012.2189692 |
| [3] | Saeidi Chiya, Hodjatkashani Farrokh, Fard Azim. New tube-based shooting and bouncing ray tracing method[C]//Proc IEEE ATC. Hai Phong: IEEE, 2009: 269-273. |
| [4] | Chen Shin-Hon, Jeng Shyh-Kang. SBR image approach for radio wave propagation in tunnels with and without traffic[J]. IEEE Trans Veh Technol, 1996, 45(3): 570–578. doi: 10.1109/25.533772 |
| [5] | Chen Shin-Hon, Jeng Shyh-Kang. An SBR/image approach for radio wave propagation in indoor environments with metallic furniture[J]. IEEE Trans Antennas Propagat, 1997, 45(1): 98–106. doi: 10.1109/8.554246 |
| [6] | Yang Chang-Fa, Wu Boau-Cheng, Ko Chuen-Jyi. A ray-tracing method for modeling indoor wave propagation and penetration[J]. IEEE Trans Antennas Propagat, 1998, 46(6): 907–919. doi: 10.1109/8.686780 |
| [7] | Bernardi Paolo, Cicchetti Renato, Testa Orlandino. An accurate UTD model for the analysis of complex indoor radio environments in microwave WLAN systems[J]. IEEE Trans Antennas Propagat, 2004, 52(6): 1509–1520. doi: 10.1109/TAP.2004.830260 |
| [8] | Xu Feng, Jin Yaqiu. Bidirectional analytic ray tracing for fast Computation of composite scattering from electric-large target over a randomly rough surface[J]. IEEE Trans Antennas Propagat, 2009, 57(5): 1495–1505. doi: 10.1109/TAP.2009.2016691 |
| [9] |
刘建新, 高攸纲. 几何绕射理论应用中的后向射线跟踪问题[J]. 北京邮电大学学报, 1996, 19(2): 27–32.
Liu Jianxin, Gao Yougang. The problem of backward ray tracing in application of geometrical theory of diffraction[J]. Journal of Beijing University of Posts and Telecommunications, 1996, 19(2): 27–32. |
| [10] | Zhou Xiao, Zhu Jiyue, Yu Weiming, et al. Time-domain shooting and bouncing rays method based on beam tracing technique[J]. IEEE Trans Antennas Propagat, 2015, 63(9): 4037–4048. doi: 10.1109/TAP.2015.2448757 |
| [11] | Norman R J, Bennett J A, Dyson P L, et al. A ray-tracing technique for determining ray tubes in anisotropic media[J]. IEEE Trans Antennas Propagat, 2013, 61(5): 2664–2675. doi: 10.1109/TAP.2013.2240647 |


