为了保护图像边缘、细节等信息,建立了l1范数约束的非局部均值正则模型.首先通过实验证明了非局部均值去噪算法余项的概率密度函数具有较强的拖尾性质,符合Laplace分布的特点.基于此,使用l1范数约束的非局部均值去噪算法余项作为新的正则项,提出了新的正则模型.然后利用Bregman算子分裂算法求解得到相应的优化算法,并且可将新算法看成Plug-and-Play Priors算法的推广.实验结果表明,新模型在去除模糊,保护图像边缘、细节等信息方面的性能都优于l2范数约束的非局部均值正则模型和Plug-and-Play Priors模型.
An l1-nonlocal means regularization model was proposed in order to preserve the edges and details while deblurring the blurred image. Firstly, the article empirically gave out that the distribution of the residual in the nonlocal means denoising algorithm (differences between the noisy image and the denoised result) is heavy-tailed, which well fits the Laplacian distribution. Based on this observation, a new regularization model was proposed by using the l1-norm constrained residual as the new regularization term. Then the corresponding optimization algorithm was designed by utilizing the Bregmanized operator splitting algorithm, which can be regarded as an extension of plug-and-play Priors algorithm. Experiments show that the new model achieves better performance than the l2-nonlocal means regularization model and the plug-and-play priors model in terms of both restoration results and preserving the edges and details of the image.
图像去模糊是图像恢复[1]中最重要的研究问题之一.通常图像模糊过程可用模型[2]表示为
| $ \mathit{\boldsymbol{f}} = \mathit{\boldsymbol{A}} * \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{k}} $ | (1) |
其中:f∈RN(N=n×n)为含有噪声的模糊观测图像;A为模糊卷积算子,也称为点扩展函数或卷积核;*为卷积运算,它使图像模糊;u∈RN为原始图像;k∈RN是方差为σ2, 均值为0的高斯白噪声.图像非盲去模糊的任务[3]是利用已知含有噪声的模糊图像f和卷积核A估计真实的清晰图像u.
图像去模糊问题是高度病态的.正则化方法通过加入原始图像的先验信息引入正则项[4],使图像去模糊问题可以得到一个稳定的解.该方法易于求解,因此得到广泛关注. 2006年,Buades等[5]提出了非局部均值(NLM, nonlocal means)正则模型;2013年,Wang等[6]在Buades等[5]提出的NLM正则模型的基础上,提出了l2范数约束的NLM(l2-NLM)正则模型,并取得了很好的去模糊效果.然而,笔者通过实验验证了NLM去噪算法余项的概率密度函数更加逼近Laplace分布,而非Gaussian分布,因此使用NLM去噪算法余项的l1范数作为先验约束比l2范数更能刻画原始图像的先验信息.基于此,笔者提出了l1范数约束的NLM(l1-NLM)正则模型和相应的优化算法.该算法还可以看成是文献[7-8]中描述的Plug-and-play priors(P3)算法的推广.实验结果表明,所提出的模型和算法在去除模糊及保护图像边缘、细节等方面优于目前常用的NLM模型(如l2-NLM模型、P3-NLM模型等).
1 相关工作 1.1 NLM去噪算法NLM[9]去噪算法的主要思想是:重构图像中每个像素点的值由噪声图像中所有像素点的值通过加权平均估计得到,其中权函数是根据对应像素点之间的相似性度量来确定的.由于NLM算法在计算每个像素的过程中应用了非局部思想和图像的自相似性,所以取得了很好的去噪效果.
1.2 l2-NLM正则模型Buades等[5]在2006年创新性地使用l2范数约束的NLM去噪算法余项作为正则项,即正则项为‖u-NLMf(u)‖22,则该模型可描述为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat u}} = \mathop {\arg \min }\limits_\mathit{\boldsymbol{u}} \left\| {\mathit{\boldsymbol{u}} - {\rm{NL}}{{\rm{M}}_f}\left( \mathit{\boldsymbol{u}} \right)} \right\|_2^2}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\left\| {\mathit{\boldsymbol{A}} * \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{f}}} \right\|_2^2 \le {\sigma ^2}} \end{array} $ | (2) |
其中:‖·‖22表示l2范数的二次方;NLMf(u)表示在执行NLM去噪算法时,权重值由观测图像f计算得到,而像素值由原始图像u得到.
Wang等[6]在Buades等[5]提出的NLM正则模型的基础上,通过对NLM去噪算法NLM(·)的权重进行改进,提出了l2-NLM正则模型.该模型可描述为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat u}} = \mathop {\arg \min }\limits_u \left\| {\mathit{\boldsymbol{u}} - {\rm{NL}}{{\rm{M}}_u}\left( \mathit{\boldsymbol{u}} \right)} \right\|_2^2}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\left\| {\mathit{\boldsymbol{A}} * \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{f}}} \right\|_2^2 \le {\sigma ^2}} \end{array} $ | (3) |
其中NLMu(u)表示在执行NLM去噪算法时,权重值和像素值均由原始图像u计算得到,并且NLMu(u)可近似估计为
| $ {\mathit{\boldsymbol{u}}^{k + 1}} = {\rm{NL}}{{\rm{M}}_{{u^k}}}\left( {{\mathit{\boldsymbol{u}}^k}} \right) $ | (4) |
利用Zhang等[10]提出的Bregman算子分裂(BOS, Bregmanized operator splitting)算法对式(3)迭代求解:
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{v}}^{k + 1}} = {\mathit{\boldsymbol{u}}^k} - \delta {\mathit{\boldsymbol{A}}^{\rm{T}}} * \left( {\mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^k} - {\mathit{\boldsymbol{f}}^k}} \right)\\ {\mathit{\boldsymbol{u}}^{k + 1}} = \mathop {\arg \min }\limits_u \left( {\left\| {\left. {\mathit{\boldsymbol{u}} - {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right)} \right)} \right\|_2^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\lambda \left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{v}}^{k + 1}}} \right\|_2^2} \right)\\ {\mathit{\boldsymbol{f}}^{k + 1}} = {\mathit{\boldsymbol{f}}^k} + \mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^{k + 1}} \end{array} \right\} $ | (5) |
其中:δ为常参数,λ为正则化参数,uk为迭代恢复图像,fk、vk为含有噪声的迭代模糊图像.
式(5)中第2步可以通过求导得到
| $ {\mathit{\boldsymbol{u}}^{k + 1}} = \frac{1}{{1 + \lambda }}{\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right) + \frac{\lambda }{{1 + \lambda }}{\mathit{\boldsymbol{v}}^{k + 1}} $ | (6) |
式(6)可以理解为NLM的结果补充了一个惯性项.所以,l2-NLM模型用BOS求解可完整写为
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{v}}^{k + 1}} = {\mathit{\boldsymbol{u}}^k} - \delta {\mathit{\boldsymbol{A}}^{\rm{T}}} * \left( {\mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^k} - {\mathit{\boldsymbol{f}}^k}} \right)\\ {\mathit{\boldsymbol{u}}^{k + 1}} = \frac{1}{{1 + \lambda }}{\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right) + \frac{\lambda }{{1 + \lambda }}{\mathit{\boldsymbol{v}}^{k + 1}}\\ {\mathit{\boldsymbol{f}}^{k + 1}} = {\mathit{\boldsymbol{f}}^k} + \mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^{k + 1}} \end{array} \right\} $ | (7) |
实际上,早在2005年Buades等[9]就将原始图像u与其经过去噪算法处理的图像的差定义为方法噪声.由于干净图像u经过NLM去噪算法处理后基本不变,即NLM(u)可以近似看成原始图像u,所以u-NLMu(u)是稀疏的.与此同时,Buades等[9]给出了一些不同去噪算法作用下的方法噪声图像,如图 1所示.

|
图 1 自然图像的方法噪声实验 |
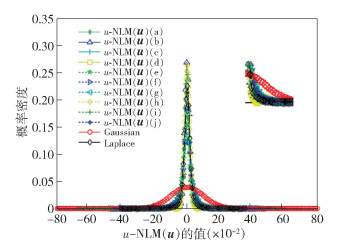
基于以上分析,u-NLMu(u)是稀疏的,因此理论上u-NLMu(u)的概率密度函数应该近似服从Laplace分布.为了更加明确地表明上述结论的合理性,笔者对u-NLMu(u)进行了概率密度函数分布的拟合实验.为了使验证结果准确合理,选取的10张测试图包括多结构图像、多纹理图像、既有纹理又有结构的图像等,如图 2所示.结果表明,其概率密度函数更加逼近Laplace分布而非Gaussian分布,如图 3所示.由于Gaussian分布的最大后验估计可以用l2范数刻画[11],而Laplace分布可以用l1范数刻画[11],所以使用u-NLMu(u)的l1范数作为先验约束比l2范数作为先验约束更能刻画图像的先验信息.

|
图 2 从上到下、从左到右标签为(a)~(j)的10张测试图 |
|
图 3 不同图像u-NLMu(u)的概率密度函数分布 |
基于此,提出了l1-NLM正则模型:
| $ \begin{array}{*{20}{c}} {\mathit{{\hat u}} = \arg \mathop {\min }\limits_u {{\left\| {\mathit{\boldsymbol{u}} - {\rm{NL}}{{\rm{M}}_u}\left( \mathit{\boldsymbol{u}} \right)} \right\|}_1}}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\left\| {\mathit{\boldsymbol{A}} * \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{f}}} \right\|_2^2 \le {\sigma ^2}} \end{array} $ | (8) |
其中‖·‖1表示l1范数.
2.2 模型的求解根据BOS算法求解式(8):
| $ {\mathit{\boldsymbol{v}}^{k + 1}} = {\mathit{\boldsymbol{u}}^k} - \delta {\mathit{\boldsymbol{A}}^{\rm{T}}} * \left( {\mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^k} - {\mathit{\boldsymbol{f}}^k}} \right) $ | (9) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}^{k + 1}} = \mathop {\arg \min }\limits_u \left( {{{\left\| {\mathit{\boldsymbol{u}} - {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right)} \right\|}_1} + } \right.}\\ {\left. {\lambda \left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{v}}^{k + 1}}} \right\|_2^2} \right)} \end{array} $ | (10) |
| $ {\mathit{\boldsymbol{f}}^{k + 1}} = {\mathit{\boldsymbol{f}}^k} + \mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^{k + 1}} $ | (11) |
其中关键问题是式(10)的求解.实际上,令u-NLMvk+1(vk+1)=p,则式(10)可写成
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}^{k + 1}} = \mathop {\arg \min }\limits_u \left( {\lambda \left\| {\mathit{\boldsymbol{p}} - \left( {{\mathit{\boldsymbol{v}}^{k + 1}} - {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right)} \right)} \right\|_2^2 + } \right.}\\ {\left. {{{\left\| \mathit{\boldsymbol{p}} \right\|}_1}} \right)} \end{array} $ | (12) |
这是l1正则下的逼近问题,使用软阈值方法求解[12],得到
| $ {\mathit{\boldsymbol{u}}^{k + 1}} = {T_{\frac{1}{{2\lambda }}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}} - {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right)} \right) + {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right) $ | (13) |
其中Tα:Rn→Rn定义[12]为
| $ {T_\alpha }\left( {{x_i}} \right) = \max \left\{ {\left| {{x_i}} \right| - \alpha ,0} \right\}{\mathop{\rm sgn}} \left( {{x_i}} \right) $ |
式(13)可以理解为NLM的结果补充了一个阈值项,则式(9)~式(11)可以整理为
| $ {\mathit{\boldsymbol{v}}^{k + 1}} = {\mathit{\boldsymbol{u}}^k} - \delta {\mathit{\boldsymbol{A}}^{\rm{T}}} * \left( {\mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^k} - {\mathit{\boldsymbol{f}}^k}} \right) $ | (14) |
| $ {\mathit{\boldsymbol{u}}^{k + 1}} = {T_{\frac{1}{{2\lambda }}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}} - {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right)} \right) + {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right) $ | (15) |
| $ {\mathit{\boldsymbol{f}}^{k + 1}} = {\mathit{\boldsymbol{f}}^k} + \mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^{k + 1}} $ | (16) |
根据式(14)~式(16),l1-NLM模型的求解可描述为算法1.对l1-NLM模型和l2-NLM模型分别使用BOS算法迭代求解后发现,l1-NLM算法与l2-NLM算法的不同点仅在式(15)和式(6),这表明新模型在计算复杂性上和原来的模型相当,但处理的意义却明显不同.式(6)为迭代噪声模糊图像vk+1经NLM去噪算法处理后的图像与vk+1加权平均,而式(15)增加了vk+1经NLM去噪算法处理后的图像与vk+1残差的阈值.相比l2-NLM模型的简单加权平均而言,l1-NLM模型加入的残差的阈值中既去除了噪声,同时又含有丰富的边缘细节信息,这与迭代正则化[13]的思想是完全一致的,因而能达到更好地保护图像边缘和细节信息的目的.
算法1 l1-NLM正则图像去模糊算法
输入:含噪模糊图f,模糊核A,参数σ、δ
预处理:Tikhonov正则去卷积方法[14]对f进行处理,得u0.
初始值:k=0,u0,f0=f,f.
while k≤迭代次数
更新v:
| $ {v^{k + 1}} = {\mathit{\boldsymbol{u}}^k} - \delta {\mathit{\boldsymbol{A}}^{\rm{T}}} * \left( {\mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^k} - {\mathit{\boldsymbol{f}}^k}} \right) $ |
更新u:
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}^{k + 1}} = {T_{\frac{1}{{2\lambda }}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}} - {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right)} \right) + \\ {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right) \end{array} $ |
更新f:
| $ {\mathit{\boldsymbol{f}}^{k + 1}} = {\mathit{\boldsymbol{f}}^k} + \mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^{k + 1}} $ |
更新k:
k+ +
end
输出:uk.
值得注意的是,当λ=0时,式(15)可退化为
| $ {\mathit{\boldsymbol{u}}^{k + 1}} = {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right) $ | (17) |
退化算法可完整写为
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{v}}^{k + 1}} = {\mathit{\boldsymbol{u}}^k} - \delta {\mathit{\boldsymbol{A}}^{\rm{T}}} * \left( {\mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^k} - {\mathit{\boldsymbol{f}}^k}} \right)\\ {\mathit{\boldsymbol{u}}^{k + 1}} = {\rm{NL}}{{\rm{M}}_{{v^{k + 1}}}}\left( {{\mathit{\boldsymbol{v}}^{k + 1}}} \right)\\ {\mathit{\boldsymbol{f}}^{k + 1}} = {\mathit{\boldsymbol{f}}^k} + \mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}} * {\mathit{\boldsymbol{u}}^{k + 1}} \end{array} \right\} $ | (18) |
这与文献[7-8]中描述的Plug-and-Play Priors算法一致,记为P3-NLM算法. l2-NLM算法、l1-NLM算法、P3-NLM算法的区别仅在式(6)、式(15)、式(17).相对于式(17)而言,式(6)和式(15)均有余项加回到恢复图像中,该余项中均含有丰富的边缘细节信息,所以理论上l2-NLM模型和l1-NLM模型比P3-NLM模型在保护图像边缘、细节信息方面有更好的性能.
3 仿真实验及分析在仿真实验中,所用的图像均为256×256的灰度图,如图 4所示.为了验证所提模型和算法的性能表现,实验设定以下3组初始条件.

|
图 4 实验所用的测试图 注:从上到下、从左到右15张实验图分别为Lenna、Peppers、Man、Boat、Barbara、Baboon、House、Hill、Patches、Couple、Bank、Hat、Reagan、Women、Columbia |
A组:实验所用图像均加有7×7的均值模糊核和标准差为5的高斯白噪声.
B组:实验所用图像均加有9×9的均值模糊核和标准差为5的高斯白噪声.
C组:实验所用图像均加有7×7的均值模糊核和标准差为10的高斯白噪声.
与其对比的模型有Buades等[5]提出的非局部正则模型、P3-NLM模型[7]、l2-NLM模型[6].采用以上模型作为对比,原因如下:
1) 以上模型是可实现的,并且会得到一个稳定的结果.
2) 所提新模型是以上模型的改进,且都是基于正则化方法所提出的.
采用2两个标准来衡量实验恢复图像的质量,①数值结果,即峰值信噪比[15](PSNR, peak signal to noise ratio)、结构相似度[15](SSIM, structural similarity index metric);②视觉效果.并且,所有实验均在Windows 7操作系统下,4 GB内存、Inter-Xeon 2.40 GHz的计算机上由Matlab2012b完成.为了保证测试的有效性,在所有的测试实验中的参数均保持一致,即δ=1.01,λ=0.015,k=10.
表 1和表 2给出了在相同模糊和噪声强度下Buades等[5]提出的非局部正则模型、P3-NLM模型、l2-NLM模型和l1-NLM模型对15张测试图去模糊的具体表现,包括PSNR值和SSIM值.从实验结果可以看出,和Buades等[5]提出的非局部正则模型相比,所提出的l1-NLM模型PSNR平均值比其高1 dB左右,SSIM平均值比其高0.6左右;与P3-NLM模型相比,l1-NLM模型的PSNR平均值比其高0.3 dB左右,SSIM平均值比其高0.02左右;和l2-NLM模型相比,l1-NLM模型的PSNR平均值比其高0.2 dB左右,SSIM平均值比其高0.02左右.因此,l1-NLM模型的PSNR值和SSIM值相对于其他模型均有提升.由表 3~表 6所示结果可看出,其他的模糊尺度和噪声水平下的实验,l1-NLM模型也得到了相对较优的数值结果.
|
|
表 1 A组实验条件下不同去模糊方法的PSNR值 |
|
|
表 2 A组实验条件下不同去模糊方法的SSIM值 |
|
|
表 3 B组实验条件下不同去模糊方法的PSNR值 |
|
|
表 4 B组实验条件下不同去模糊方法的SSIM值 |
|
|
表 5 C组实验条件下不同去模糊方法的PSNR值 |
|
|
表 6 C组实验条件下不同去模糊方法的SSIM值 |
图 5、图 6分别给出了部分图像经上述方法处理后的视觉效果对比结果.从局部放大信息(图像右上角)所示结果可知,l1-NLM模型对Lenna图像中的人脸细节特征和Man图像中的建筑物边缘有很好的保护作用.

|
图 5 A组实验条件下不同方法对Lenna处理视觉效果 |

|
图 6 A组实验条件下不同方法对Man处理视觉效果 |
基于正则化图像去模糊问题中正则项的好坏直接影响图像去模糊效果.笔者通过验证u-NLMu(u)的概率密度函数近似逼近Laplace分布,在l2-NLM模型的基础上提出了l1-NLM模型,该模型能够更好地刻画图像的先验信息.然后,结合BOS算法给出了l1-NLM优化算法.实验结果表明,所提出的新模型和算法与同类其他图像去模糊方法相比,具有更好的视觉效果和数值表现.
| [1] | Banham M R, Katsaggelos A K. Digital image restoration[J]. IEEE Signal Processing Magazine, 1997, 14(2): 24–41. doi: 10.1109/79.581363 |
| [2] | Teodoro A M, Bioucas-Dias J M, Figueiredo M A T. Image restoration and reconstruction using variable splitting and class-adapted image priors[C]//IEEE International Conference on Image Processing. Phoenix: IEEE, 2016: 3518-3522. |
| [3] | Xu Jianlou, Feng Aifen, Hao Yan, et al. Image deblurring and denoising by an improved variational model[J]. AEU-International Journal of Electronics and Communications, 2016, 70(9): 1128–1133. doi: 10.1016/j.aeue.2016.05.008 |
| [4] | Lou Yifei, Zhang Xiaoqun, Osher S, et al. Image recovery via nonlocal operators[J]. Journal of Scientific Computing, 2010, 42(2): 185–197. doi: 10.1007/s10915-009-9320-2 |
| [5] | Buades A, Coll B, Morel J M. Image enhancement by non-local reverse heat equation[J]. Preprint CMLA, 2006(22): 2001–2016. |
| [6] | Wang Zhiming, Bao Hong. A new regularization model based on non-local means for image deblurring[J]. Applied Mechanics and Materials, 2013(411): 1164–1169. |
| [7] | Sreehari S, Venkatakrishnan S V, Wohlberg B, et al. Plug-and-play priors for bright field electron tomography and sparse interpolation[J]. IEEE Transactions on Computational Imaging, 2016, 2(4): 408–423. |
| [8] | Chan S H, Wang Xiran, Elgendy O A. Plug-and-play ADMM for image restoration:fixed-point convergence and applications[J]. IEEE Transactions on Computational Imaging, 2017, 3(1): 84–98. doi: 10.1109/TCI.2016.2629286 |
| [9] | Buades A, Coll B, Morel J M. A non-local algorithm for image denoising[C]//IEEE Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005: 60-65. |
| [10] | Zhang Xiaoqun, Burger M, Bresson X, et al. Bregmanized nonlocal regularization for deconvolution and sparse reconstruction[J]. Siam Journal on Imaging Sciences, 2010, 3(3): 253–276. doi: 10.1137/090746379 |
| [11] | Lanza A, Morigi S, Sgallari F, et al. Variational image denoising while constraining the distribution of the residual[J]. Electronic Transactions on Numerical Analysis, 2014(42): 64–84. |
| [12] | Zuo Wangmeng, Gu Shuhang, Ren Dongwei, et al. Learning iteration-wise generalized shrinkage thresholding operators for blind deconvolution[J]. IEEE Transactions on Image Processing, 2016, 25(4): 1751–1764. |
| [13] | Osher S, Burger M, Goldfarb D, et al. An iterative regularization method for total variation-based image restoration[J]. Multiscale Modeling and Simulation, 2005, 4(2): 460–489. doi: 10.1137/040605412 |
| [14] | Tikhonov A N, Arsenin V Y. Solution of ill-posed problems[J]. Mathematics of Computation, 1977, 32(144): 491–491. |
| [15] | Feng Xiangchu, Li Xiaohui, Wang Weiwei, et al. Improvement of BM3D algorithm based on wavelet and directed diffusion[C]//International Conference on Machine Vision and Information Technology. Singapore: IEEE, 2017: 28-33. |


