2. 中国科学院 信息工程研究所, 北京 100093
机会传感网络的连通性具有时间演化性,很难用传统的图模型直接建模.为此,采用时间图对机会传感网络的连通性进行建模,通过时间路径、时间距离和连通效率计算得到整网连通度,提出采用整网连通度表征机会传感网络的连通性能.仿真实验结果表明,整网连通度能够较准确地反映不同实验场景下的网络连通性.
2. Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China
Connectivity is an important metric to reflect the performance of network. Connectivity of opportunistic sensor networks (OSN) is of temporal evolution, which is hard to be modeled with traditional graph model. Connectivity of OSN is modeled with temporal graph, and network connectivity degree is achieved by computing temporal path, temporal distance, and connectivity effectiveness. Furthermore, network connectivity degree is proposed to depict connectivity of OSN. The simulation results show that network connectivity degree can reflect connectivity of OSN more accurately in different experiment scenarios.
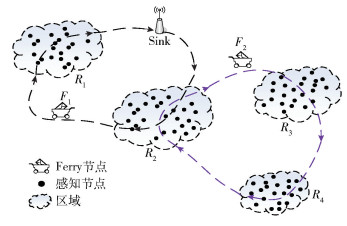
机会传感网络(OSN, opportunistic sensor networks)是一种利用节点移动带来相遇机会实现通信的自组织网络[1],能够以较低成本实现大范围感知,具有延迟容忍网络(DTN, delay tolerant networks)的间歇连接、频繁割裂、时延高等特征,其网络连通状态变化频繁.如图 1所示,各监测区域(Region)内节点感知到的消息通过移动节点(Ferry)携带转发至汇聚节点(Sink),实现整网连通.
|
图 1 机会传感网络场景示意图 |
目前,国内外对机会传感网络的研究主要致力于转发机制、节点移动模型[2]和缓存管理.连通性作为衡量网络性能的重要指标,是保证网络正常运行的前提.由于OSN的网络拓扑变化频繁,无法用传统的图模型对其直接建模,从而对准确获取网络连通性带来了巨大的挑战.笔者研究了OSN的连通性表征方法,为OSN连通性的进一步研究提供参考.
1 相关工作Adhoc网络中,节点传输半径、节点度、节点密度等因素对连通性具有重要影响. Xue等[3]基于占用理论分析了节点度和网络连通性的关系,指出均匀分布的网络中,当平均节点度小于0.074 log n时,网络近似不连通,平均节点度高于5.177 4log n时,网络近似1连通;Wan等[4]基于随机几何图理论,分析了在节点均匀分布的单位面积区域中网络保持k连通所需的渐近临界传输半径.上述研究针对节点部署较为密集的网络,不适合用来分析网络拓扑较为稀疏且长时间处于分割状态下的OSN.
根据DTN网络的消息传递特性,可采用演化图(EG, evolving graph)和时间图(TG, temporal graph)[5]对DTN网络建模,将动态网络划分为连续的快照序列(snapshot),分析其拓扑变化规律. Chaintreau等[6]采用随机时间图对机会网络建模,提出求解动态网络时间直径(temporal diameter)的方法,实验结果表明,时间直径越短,网络的连通性越高;Nicosia等[7]基于时变图理论(TVG, time varying graph)分析了DTN的最大连通分量,并提出了最大连通分量的计算方法. OSN以Sink节点为中心,感知消息按照一定规律流向Sink节点,连通分量、网络直径不能准确地反映整网的连通性.
为了较准确地表征OSN的连通性,根据OSN的特性,采用时间图对其进行连通性建模,定义整网连通度为表征机会传感网络连通性的参数;定期从网络获取快照,生成网络快照集,并将其转化成邻接矩阵集;通过邻接矩阵集计算整网连通度.
2 连通性建模针对多感知区域的环境监测,每个区域采用传感网络进行部署.设区域内节点密集,连通程度较高,可将OSN中的单个感知区域抽象成一个感知节点.
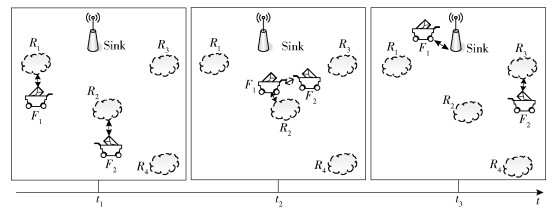
2.1 时间图模型为了获得网络的拓扑信息,从t0时刻开始,每隔时间步Δt获取一次网络快照. t1(t1=t0+Δt)时刻的网络快照为G(t1),将G(t1)作为区间[t1-Δt, t1]内的网络拓扑,则从t0时刻起,每隔Δt的网络快照序列为{G(t1), G(t2), …, G(tτ)},如图 2所示.
|
图 2 网络快照 |
定义1 时间图Gt0, tτ={G(t1), G(t2), …, G(tτ)}是离散时间t0 < t1 < … < tτ∈T=[t0, tτ]下的有序图集.其中,G(t)=(V(t), E(t))表示G在t(t∈[t0, tτ])时刻的时间子图,V(t)和E(t)分别表示t时刻的顶点集和边集,且对于∀t∈[t0, tτ],有|V(t)|=N.
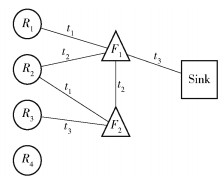
网络运行过程中,节点的数量不变,因此可将各快照的相关信息合并,如图 3所示.虽然每个快照下的网络都不连通,但是依靠Ferry的移动,区域R1、R2的消息能够传递至Sink.可见,时间图模型适用于节点间歇性链接、拓扑频繁变化的网络,如OSN.
|
图 3 时间图模型 |
时间图中,消息传递路径具有典型的时向性,不能用传统的“路径”来描述.根据图 3给出时间路径的定义如下.
定义2 时间[t0, tτ]内,{V1, V2, …, Vn}为时间图Gt0, tτ上的不重复节点集合,若存在与之对应的时间序列{t1, t2, t3, …, tδ},即t0≤t1≤t2≤…≤tδ≤tτ,且对任意两节点i、j,满足V1≡i, Vn≡j,则称存在时间路径,使得节点i通向节点j,记为ψij(t0, tτ).
ψij(t0, tτ)=∞表明节点i至节点j不存在时间路径. 图 3中,[t0, t3]内,R4不存在通向Sink节点的时间路径,则ψR4S(t0, tτ)=∞,S表示Sink节点.
定义3 时间[t0, tτ]内,任意两节点i、j之间的最短时间路径称为节点i至节点j的时间距离,记为Dij(t0, tτ),则
| $ {{D}_{ij}}({{t}_{0}}, {{t}_{\tau }})=\text{min}\{{{\psi }_{ij}}({{t}_{0}}, {{t}_{\tau }})\} $ | (1) |
如图 3所示,R2到F2存在2条时间路径:
Dij(t0, tτ)=∞表明,节点i至节点j不存在时间路径.节点之间的时间距离越短,表明节点间连通效率越高.为便于分析,对节点距离进行归一化处理,得到连通效率[8]以反映节点间的连通情况.
定义4 连通效率为
| $ {H_{ij}}({t_0}, {t_\tau }) = \left\{ \begin{array}{l} 0{\rm{, }}\;\;\;{D_{ij}}({t_0}, {t_\tau }) = \infty \\ \frac{{{t_\tau }{\rm{-}}{D_{ij}}({t_0}, {t_\tau })}}{{{t_\tau }}}, \;\;\;{D_{ij}}({t_0}, {t_\tau })\tau \end{array} \right. $ | (2) |
其中Dij(t0, tτ)=∞表示节点i、j在时间段[t0, tτ]内的时间距离.节点间的连通效率越高,表明节点间能在越短的时间内形成直接或间接的“连通链路”,即两节点间的连通性越好.
定义5 网络中各区域至Sink的连通效率均值称为整网连通度
| $ C({t_0}, {t_\tau }) = \frac{1}{P}\sum\limits_{i = 1}^P {{H_{is}}({t_0}, {t_\tau })} $ | (3) |
其中P表示网络中感知区域的个数.
2.2 网络快照的时间间隔为了准确反映网络拓扑的变化情况,根据网络的平均演化速度确定获取网络快照的时间间隔Δt.计算所有Ferry节点的平均相遇间隔时间,取最小平均相遇间隔时间作为获取网络快照的时间间隔Δt.
时间T内,假设Ferry节点Fi与区域、Ferry或Sink发生X次相遇,Fi(tx)为第x次(x≤X)相遇的开始时间,则平均相遇间隔时间为
| $ \lambda ({F_i}) = \frac{1}{X}\sum\limits_{x = 1}^{X{\rm{ - }}1} {[{F_i}({t_{x + 1}}){\rm{ - }}{F_i}({t_x})]} \; $ | (4) |
取其中最小平均相遇间隔时间,得到获取网络快照的时间间隔
| $ \Delta t = {\rm{min}}\left\{ {\sum\limits_{i = 1}^Q {\lambda ({F_i})} } \right\}\; $ | (5) |
其中Q表示网络中Ferry节点数量.
3 整网连通度 3.1 算法设计通过时间片所对应的邻接矩阵序列计算整网连通度.
定义6 静态无向图G(V, E)由n个节点V={v1, v2, …, vn}和m条边E={〈v1, v2〉, 〈v2, v3〉, …, 〈vn-1, vn〉}构成,对应的n阶方阵A=(auv)(u, v∈V)称图G的邻接矩阵.
若节点u和v之间存在连边,则auv=1;否则auv=0.假设在时间图Gt0, tτ={G(t1), G(t2), …, G(tτ)}中,t(t0〈t<tτ)时刻对应的邻接矩阵为A(t),可达矩阵的计算公式为
| $ \begin{array}{l} \mathit{\boldsymbol{Y}} = {\left[{\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{A}}\left( t \right)} \right]^\theta } = \\ \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{A}}^2}\left( t \right) + \cdots + {\mathit{\boldsymbol{A}}^3}\left( t \right) + \cdots + {\mathit{\boldsymbol{A}}^\theta }\left( t \right) \end{array} $ | (6) |
其中I表示单位矩阵.易知,节点u和v之间长度小于等于θ的路径数量为Yuv.由于实际情况中Ferry节点的数量不会太多,在同一个网络快照中最长路径几乎都小于2,因此这里仅考虑3以内的情况.令B(t)=[I+A(t)]3,若B(t)uv≠0,表示节点u、v之间可达.
若时间图Gt0, tτ={G(t1), G(t2), …, G(tτ)}所对应的邻接矩阵序列为A(t1), A(t2), …, A(tτ),令
| $ {\mathit{\boldsymbol{B}}_m} = \mathit{\boldsymbol{B}}({t_1})\mathit{\boldsymbol{B}}({t_2}) \cdots \mathit{\boldsymbol{B}}({t_m})({t_m} \le {t_\tau }) $ | (7) |
显然,若(Bm)ij≠0(i≠j, i≤n, j≤n),表示节点i、j之间存在时间路径.且由定义3可知,若(Bm)ij≠0且(Bm-1)ij=0,则Dij(t0, tτ)=tm.
根据式(2)、式(3)可计算整网连通度,算法描述如下.
算法1 连通度算法
输入:邻接矩阵集、感知区域个数P、时间段[t0, tτ]
输出:整网连通度
步骤1 由邻接矩阵集初始化d阶邻接矩阵数量K,由感知区域个数P初始化区域延时队列L.
步骤2 将第k个邻接矩阵赋值给d阶矩阵B,同时初始化循环控制变量k=0.
步骤3 k=k+1;若k满足k≤K,则转向步骤4;否则转向步骤7.
步骤4 计算第k+1个邻接矩阵所对应的时间距离B=B[I+A(k)]3.
步骤5 若在B中有区域Ri与Sink节点所对应的位置第1次出现非零值,转向步骤6;否则返回步骤3.
步骤6 区域Ri与Sink节点的连通效率时间距离为
| $ {H_{{R_i}S}}({t_0}, {t_\tau }) = \frac{{k\Delta t}}{{{t_\tau }{\rm{-}}{t_0}}} $ | (8) |
将其填入对应的区域延时队列L中,判断L中是否包含所有区域到Sink节点的连通效率,若包含,转向步骤7;否则,返回步骤3.
步骤7 计算L中区域时间距离的算数平均值,得到并输出整网连通度.
3.2 算法分析设感知区域个数为P,移动节点个数为Q,时间片个数为Z.算法中辅助矩阵大小为(P+Q+1)2,辅助数组大小为P,因此空间复杂度为O((P+Q)2).计算整网连通度时,需要连续计算矩阵的乘法,使得时间复杂度较大,达到O(Z(P+Q+1)3),但是矩阵的维度较小,计算网络连通度所消耗的时间尚可接受.
4 仿真实验 4.1 实验参数及测试指标在机会传感网络仿真工具(ONE, opportunistic network environment simulator)下,网络消息投递成功率[8]可反映网络的实际连通情况,主要的实验参数设置如表 1所示.实验进行100 h,每隔20 min统计1次网络消息投递成功率和整网连通度.
|
|
表 1 主要实验参数 |
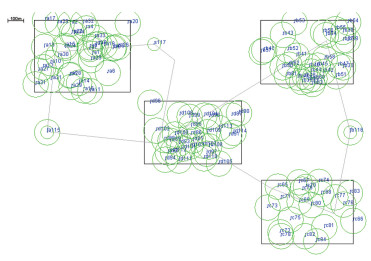
为验证新方法在不同实验场景下的适用性,设计了3种不同实验场景,如图 4所示.
|
图 4 整网连通度实验场景 |
实验1:Ferry按照设定的路线移动,数量为2.
实验2:Ferry按照设定的路线移动,数量为4.
实验3:Ferry在整网内随机移动,数量不定.
在3种不同实验场景下调整Ferry的移动速度、Ferry的半径以及Ferry的数量等影响连通性的参数.在实验1、实验2中,分别对不同网络连通状态(连通性好、连通性一般、连通性差)进行仿真.实验3中,对不同Ferry数量的网络进行了仿真.参数设置如表 2所示.
|
|
表 2 影响连通性参数 |
仿真结果如图 5~图 7所示. 3种不同实验场景下的平均网络消息投递成功率和平均整网连通度如表 3~表 5所示.

|
图 5 实验1的仿真结果 |
|
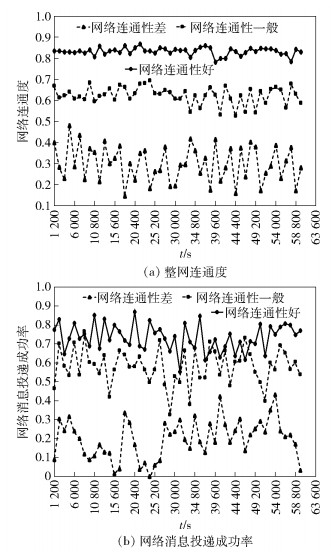
图 6 实验2的仿真结果 |
|
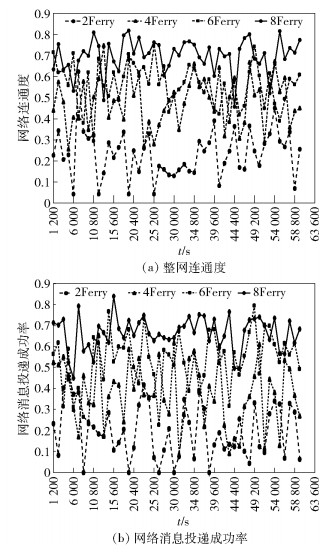
图 7 实验3的仿真结果 |
|
|
表 3 实验1场景下不同网络连通状况的效果 |
|
|
表 4 实验2场景下不同网络连通状况的效果 |
|
|
表 5 实验3场景下不同Ferry数量的效果 |
网络连通性较好时,有较强的消息传递能力,能够在比较短的时间内将区域内产生的消息投递至Sink节点,因此,各区域和Sink节点之间会有较高的连通效率,消息的投递成功率较高;网络连通性较差时,较多的区域处于分割情况下,没有时间路径连通这些区域和Sink节点,导致整网的消息投递成功率较低.从实验结果可以看出,3种不同实验场景下,采用笔者定义的整网连通度与网络消息投递成功率实测值的变化情况基本吻合,整网连通度能够反映网络的连通性状况.
理论上,随着Ferry节点数量的增加,网络连通性应有所改善.对比图 5(a)和图 6(a)可以看出,实验2中3种不同网络连通状况下的整网连通度均优于实验1.
OSN中,Ferry按照设定的路线移动应该比Ferry随机移动情况下的网络连通性好.对比图 5(a)、图 6(a)和图 7(a)可以看出,实验1和实验2表明整网连通度可以较明显地区分整网的连通性的好坏,实验3表明整网连通度在Ferry节点随机移动的场景下对连通性的好坏区分能力弱. 图 5(b)、图 6(b)和图 7(b)反映出的网络实际连通情况也说明了这一现象.
由图 4、图 5可知,采用笔者定义的整网连通度在3种不同网络连通状况下均能反映网络连通状况,说明提出的整网连通度具有适用性.
5 结束语网络连通性是衡量网络性能的重要指标,而OSN的连通性具有时间演化性,无法用传统的图模型直接进行建模.针对OSN的特点,在采用时间图对OSN的连通性进行建模的基础上,提出采用整网连通度表征OSN连通性,仿真实验验证了该方法的适用性.下一步拟对连通性模型展开深入研究,以获得能更准确刻画OSN连通性的模型,为改善OSN的性能提供依据.
| [1] | Chen Qifan, Liu Linlan, Yang Zhiyong, et al. Prediction approach of critical node based on multiple attribute decision making for opportunistic sensor networks[J]. Journal of Sensors, 2016, 2016(4): 1–8. |
| [2] |
吴大鹏, 刘佳, 王汝言. 带有投递概率感知的低开销机会网络路由机制[J]. 北京邮电大学学报, 2013, 36(6): 64–68.
Wu Dapeng, Liu Jia, Wang Ruyan. Cost-efficient routing mechanism with delivery probability perception in opportunistic networks[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(6): 64–68. |
| [3] | Xue F, Kumar P R. The number of neighbors needed for connectivity of wireless networks[J]. Wireless Networks, 2004, 10(2): 169–181. doi: 10.1023/B:WINE.0000013081.09837.c0 |
| [4] | Wan P J, Yi C W, Wang L X. Asymptotic critical transmission radius for k-connectivity in wireless Ad Hoc networks[J]. IEEE Transactions on Information Theory, 2010, 56(6): 2867–2874. doi: 10.1109/TIT.2010.2046254 |
| [5] | Scellato S, Leontiadis I, Mascolo C, et al. Evaluating temporal robustness of mobile networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(1): 105–117. |
| [6] | Chaintreau A, Mtibaa A, Massoulie L, et al. The diameter of opportunistic mobile networks[C]//Proceedings of the 2007 ACM CoNEXT Conference. New York: ACM, 2007: 1-12. |
| [7] | Nicosia V, Tang J, Musolesi M, et al. Components in time-varying graphs[J]. Chaos:An Interdisciplinary Journal of Nonlinear Science, 2012, 22(2): 1–12. |
| [8] | Harras K A, Almeroth K C. Inter-regional messenger scheduling in delay tolerant mobile networks[C]//Proceedings of the 2006 International Symposium on a World of Wireless, Mobile and Multimedia Networks. New York: IEEE Computer Society, 2006: 93-102. |


