为提高网络部署的灵活性,保障多样化虚拟网络的需求,针对无线自回传网络场景提出一种基于Lyapunov的虚拟资源分配策略.联合考虑系统稳定性、虚拟网络最小速率需求和小蜂窝回传容量限制,对无线接入资源和回传带宽进行联合分配,建立虚拟网络效用最大化模型;其次,运用Lyapunov优化理论设计了一种基于当前信道状态和队列状态的实时调度算法;最后,通过拉格朗日对偶算法和基于相似度随机变异的粒子群算法进行迭代求解.仿真结果表明,该方案可在保证系统队列稳定性的同时提高无线虚拟网络的平均总收益.
To improve the flexibility of network deployment and satisfy the diversity of virtual network demand, a virtual resource allocation strategy utilizing Lyapunov for wireless self-backhaul network was proposed. Firstly, a joint radio access resources and backhaul algorithm is deployed to maximize the virtual network utility under certain practical preconditions, i. e. the network queue stability, the minimum average data rate for each virtual network and the capacity constraint of the backhaul link. Secondly, a real-time scheduling algorithm based on the current channel state and queue state is designed by Lyapunov optimization, Lagrange duality algorithm and particle swarm algorithm based on similarity random variation. Simulation shows that the proposed method can effectively improve the total average revenue of virtual network while guaranteeing the queue stability.
随着移动用户数量的迅猛增长,下一代网络需要更高的系统容量、频谱利用率以及更低的时延[1],无线网络虚拟化技术应运而生[2].在无线网络虚拟化场景中,传统运营商被解耦成2个独立的角色:基础设备供应商(InP, infrastructure provider)和服务提供商(SP, service provider). InP将网络中的物理资源切割重组,SP则从InP租赁重组的物理资源, 为用户提供定制化服务[3-4].
由于物理资源的稀缺、SP的多样化服务质量需求,如何高效地为SP分配物理资源以提升系统性能至关重要[5]. Kamel等[6]研究了LTE单小区场景中的虚拟资源分配问题,考虑了在满足SP最小时频资源块需求下如何保证边缘用户与中心用户的公平度. Parsaeefard等[7]引入了基于速率和基于资源的切片描述,提出了一种可同时满足切片不同需求的动态资源调度方案. Zhu等[8]利用拍卖博弈理论来刻画InP与SP之间的资源映射[9]问题.
此外,由于数据业务的爆炸式增长,小蜂窝组网成为提升系统能效和谱效的主要手段之一[10].不同于传统回传技术,带内自回传技术允许小基站在回传链路与接入链路中使用相同频带,从而降低网络部署成本, 提高网络部署的灵活性[11].
针对无线自回传网络场景提出一种基于Lyapunov的虚拟资源分配策略,该方案联合考虑无线信道的时变特征、用户业务的随机到达以及缓存空间的局限性,利用Lyapunov理论设计出一种实时调度算法,并对系统时延与网络效益进行综合性地研究.
1 无线网络虚拟化和带内自回传机制 1.1 无线网络虚拟化系统架构如图 1所示,至下而上依次为InP层、虚拟层、SP层.在该系统中InP拥有网络设施、频谱资源和无线自回传链路等物理网络资源;虚拟层负责将来自InP的物理资源进行分割,并重新组成虚拟网络资源,再将抽象后的虚拟资源出租给属于不同虚拟网络的SP,而SP则通过租用的虚拟资源为其注册用户提供端到端的定制化服务.
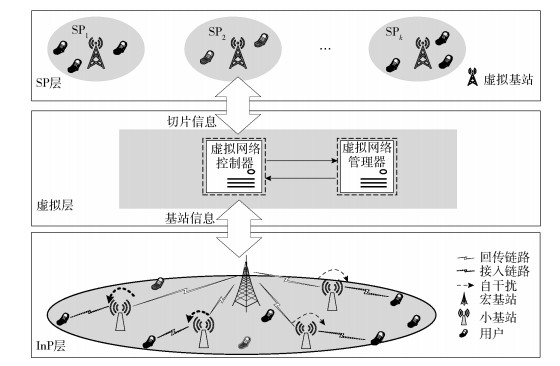
|
图 1 无线网络虚拟化框架 |
笔者致力于研究上行传输中的虚拟资源分配问题.假设网络工作在离散时隙t∈{1, 2, …, T},InP层拥有一个宏基站和N个带内自回传的小基站,用n表示基站,0为宏基站,n∈{1, 2,…, N}为小基站. K表示系统服务的SP集合,每个SPk∈K服务的用户集合表示为Uk,因此第k个SP服务的具体用户可表示为ku.
1.2 带内自回传机制在上行传输中,用户通过接入链路向小基站发送数据,小基站将接收的用户数据通过无线回传链路转发给宏基站.为了避免带内自回传引起多余的干扰源,考虑在接入链路和回传链路上使用频分复用的工作模式.
如图 2所示,系统总带宽B被切割成2个部分,即αB和(1-α)B,其中α代表带宽的切割比例.宏基站和小基站使用αB的带宽在接入链路上进行数据传输,小基站使用(1-α)B的带宽向宏基站回传数据.为实现接入链路和回传链路的容量匹配,在每个调度周期上将根据网络状态动态地调整带宽切割比例α.
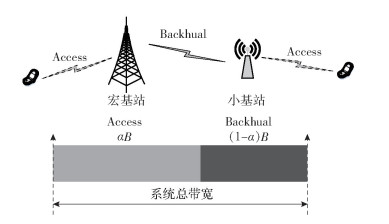
|
图 2 频谱切割示意图 |
在调度周期t上,用户ku在基站n中的瞬时频谱效率可表示为
| $ r_{{k_{\rm{u}}}}^n\left( t \right) = {\rm{lb}}\left( {1 + S_{{k_{\rm{u}}}}^n} \right) $ | (1) |
其中:
在每个调度周期,虚拟网络管理器将根据每个SP用户的信道质量和队列状态动态地调整频谱资源的分配方式.因此,在时隙t上用户ku的瞬时数据速率可表示为
| $ {R_{{k_{\rm{u}}}}}\left( t \right) = \sum\limits_{n = 0}^N {y_{{k_{\rm{u}}}}^n\left( t \right)\alpha Br_{{k_{\rm{u}}}}^n\left( t \right)} $ | (2) |
其中:ykun(t)既可代表用户ku的连接标识,也可代表用户ku在基站n中获得的频谱资源比例,ykun(t)≠0,则代表用户ku连接到基站n.
在上行回传链路,采用一种静态的频谱分配方式来避免小基站在回传链路上的干扰问题.假设小基站n分配到带宽比gn进行数据的回传,因此,小基站n的瞬时回传速率为
| $ {R^n}\left( t \right) = {g_n}\left( {1 - \alpha } \right)B{\rm{lb}}\left( {1 + \frac{{{p_n}h_n^0\left( t \right)}}{\sigma }} \right) $ | (3) |
其中:pn为小基站n在回传链路中的发射功率,hn0(t)代表小基站n到宏基站的信道增益.
2.2 SP用户业务模型假设每个SP用户都拥有一个缓存队列用于存储新到达的业务. Qku(t)表示用户ku在时隙t上的队列长度,Aku(t)表示新到达的数据包个数,假设数据包的到达过程服从参数为λku的泊松分布.因此,用户ku的队列更新过程可表示为
| $ {Q_{{k_{\rm{u}}}}}\left( {t + 1} \right) = \max \left\{ {{Q_{{k_{\rm{u}}}}}\left( t \right) + {A_{{k_{\rm{u}}}}}\left( t \right) - {Z_{{k_{\rm{u}}}}}\left( t \right),0} \right\} $ | (4) |
其中Zku(t)为在时隙中用户ku传输的数据包个数.
定义1 对于任意的队列Qku(t)∈R+,若满足
定义2 在一个队列网络中,只有当网络中所有队列都满足稳定性条件,该队列网络才严格稳定.
2.3 问题建模在无线网络虚拟化的商业模型中,SP租赁相应数量的虚拟资源为注册用户提供端到端的服务.因此,SPk在时隙k上的瞬时效用可表示为
| $ \begin{array}{*{20}{c}} {{G_k}\left( t \right) = {\omega _k}U\left( {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right) - }\\ {{\gamma _k}\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {\sum\limits_{n = 0}^N {y_{{k_{\rm{u}}}}^n\left( t \right)\alpha B - {\rho _k}G_k^b\left( t \right)} } } \end{array} $ | (5) |
其中:等式右边第1项代表SPk在时隙t中向用户提供服务而得到的收入,ωk为SPk向服务用户收取的单位费用;第2项为SPk在接入链路中租赁频谱资源的成本,γk为SP租赁无线接入链路资源的价格.
式(5)右边第3项为SPk租用无线回传链路进行数据回传的开销,ρk为回传链路的租用单价.因此,SPk在回传链路上的开销为
| $ G_k^b\left( t \right) = \sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {{Z_{{k_{\rm{u}}}}}\left( t \right)\left( {1 - \alpha } \right)B} $ | (6) |
研究目的是设计一种动态的虚拟资源调度策略,在满足用户队列稳定性和SP平均速率需求的前提下,最大化系统内SP的平均总收益.因此,资源调度问题可建立成下面的数学模型:
| $ \begin{array}{l} {\rm{P1:}}\mathop {\max }\limits_{y,\alpha } \bar G = \mathop {\lim }\limits_{T \to \infty } \sup \frac{1}{T}\sum\limits_{t = 1}^T {\left\{ {\sum\limits_{k = 1}^K {{G_k}\left( t \right)} } \right\}} \\ {\rm{s}}.\;{\rm{t}}.\;\;{C_1}:\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{k = 1}^T {\left( {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right)} \ge {R_k},\forall k\\ \;\;\;\;\;{C_2}:\sum\limits_{{k_{\rm{u}}} \in {U_n}} {y_{{k_{\rm{u}}}}^n\left( t \right)\alpha Br_{{k_{\rm{u}}}}^n\left( t \right)} \le {R^n}\left( t \right),\forall n,n \ne 0\\ \;\;\;\;\;{C_3}:0 \le y_{{k_{\rm{u}}}}^n\left( t \right) \le 1,\forall n,{k_{\rm{u}}}\\ \;\;\;\;\;{C_4}:\sum\limits_{k = 1}^K {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {y_{{k_{\rm{u}}}}^n\left( t \right)} } \le 1,\forall n\\ \;\;\;\;\;{C_5}:0 \le \alpha \le 1\\ \;\;\;\;\;{C_6}:{{\bar Q}_{{k_{\rm{u}}}}} < \infty ,\forall {k_{\rm{u}}} \end{array} $ | (7) |
其中:C1为每个SP的最小平均速率需求;C2为任意小基站n∈{1,2,…,N}的回传容量约束,其中Un为表示小基站n服务的用户集合;C3和C4为总带宽限制,限制条件C6可确保系统的队列稳定性.
问题P1是一个时间平均的随机优化问题,并且用户信道质量随时间动态变化,用户数据随机到达,系统将无法准确获取未来的信道质量信息和队列状态信息,因此,利用Lyapunov优化理论提出一种基于当前时隙状态的实时调度算法.
3 基于Lyapunov优化的理论分析首先,引入虚拟队列对时间平均约束进行转化,虚拟队列Dk(t)的更新过程可表示为
| $ {D_k}\left( {t + 1} \right) = \max \left\{ {{D_k}\left( t \right) + {R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} ,0} \right\},\forall k $ | (8) |
通常假设在t=1时系统中的所有队列均为0.
引理1 若资源调度算法可保证所有的虚拟队列Dk(t)均满足稳定性条件,则自然满足SP的平均速率约束C1.证明过程见文献[13].
由此,系统的队列状态向量可表示为Ω(t)=[Q(t),D(t)],为了量化系统队列状态向量Ω(t),Lyapunov函数定义为
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\Omega }\left( t \right)} \right) = }\\ {\frac{1}{2}\left[ {\sum\limits_{k \in K} {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {{{\left( {{Q_{{k_{\rm{u}}}}}\left( t \right)} \right)}^2}} } + \sum\limits_{k \in K} {{{\left( {{D_k}\left( t \right)} \right)}^2}} } \right]} \end{array} $ | (9) |
根据Lyapunov优化方法定义单时隙的Lyapunov偏移为
| $ \Delta \left( {\mathit{\Omega }\left( t \right)} \right) = \left. {E\left\{ {L\left( {\mathit{\Omega }\left( {t + 1} \right)} \right)} \right\} - L\left( {\mathit{\Omega }\left( t \right)} \right)\left| {\mathit{\Omega }\left( t \right)} \right.} \right\} $ | (10) |
Lyapunov偏移加罚则为单时隙Lyapunov偏移与该时隙系统内SP总收益期望的加权差:
| $ \Delta \left( {\mathit{\Omega }\left( t \right)} \right) - VE\left\{ {\sum\limits_{k = 1}^K {{G_k}\left( t \right)\left| {\mathit{\Omega }\left( t \right)} \right.} } \right\} $ | (11) |
其中V是一个权衡偏移与罚函数比重的非负常数.
引理2 在任意的系统队列状态Ω(t)和控制参数V下,一定存在一个上界,表示为
| $ \begin{array}{*{20}{c}} {\Delta \left( {\mathit{\Omega }\left( t \right)} \right) - VE\left\{ {\sum\limits_{k = 1}^K {{G_k}\left( t \right)\left| {\mathit{\Omega }\left( t \right)} \right.} } \right\} \le }\\ {\zeta + E\left\{ {\sum\limits_{k \in K} {{D_k}\left( t \right)\left[ {{R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right]\left| {\mathit{\Omega }\left( t \right)} \right.} } \right\} + }\\ {E\left\{ {\sum\limits_{k \in K} {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {\left\{ {{Q_{{k_{\rm{u}}}}}\left( t \right)\left[ {{A_{{k_{\rm{u}}}}}\left( t \right) - {Z_{{k_{\rm{u}}}}}\left( t \right)} \right]\left| {\mathit{\Omega }\left( t \right)} \right.} \right\}} } } \right\} - }\\ {VE\left\{ {\sum\limits_{k = 1}^K {{G_k}\left( t \right)\left| {\mathit{\Omega }\left( t \right)} \right.} } \right\}} \end{array} $ | (12) |
其中ζ为一个有限正常数.证明过程见附录1.
根据Lyapunov优化的设计准则,原问题P1可转化成在每个时隙t中,最小化Lyapunov偏移加罚的上界,即式(12)不等式符号的右侧部分.
算法1 基于SP收益的动态资源调度算法
1) 在每个时隙t,观察当前用户队列状态、用户信道条件和虚拟队列状态.
2) 当前时隙的资源分配方案为
| $ \begin{array}{*{20}{c}} {{\rm{P2:}}\mathop {\min }\limits_{y,\alpha } - V\sum\limits_{k = 1}^K {{G_k}\left( t \right)} - \sum\limits_{k \in K} {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {{Q_{{k_{\rm{u}}}}}\left( t \right){Z_{{k_{\rm{u}}}}}\left( t \right)} } + }\\ {\sum\limits_{k = 1}^K {{D_k}\left( t \right)\left[ {{R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right]} }\\ {{\rm{s}}.\;{\rm{t}}.\;\;{C_2} \sim {C_5}} \end{array} $ | (13) |
3) 分别根据式(4)、式(8)更新用户队列状态和SP虚拟队列状态.
4 虚拟资源调度方案受文献[14]的启发,利用分层解耦理论将问题P2解耦成两个子问题P2.1和P2.2,即首先假设频带切割比例α固定,通过求解子P2.1,获得SP用户在接入端中的频带资源调度方案y,然后基于方案y获取子问题P2.2的最优频带切割比例α,经过数次迭代后得到当前时隙的资源调度方案y*和α*,最后,虚拟网络管理器将资源调度决策通知给每一个SP用户,并更新相应的用户队列和SP虚拟队列.
4.1 SP用户在接入端的频带资源分配子问题给定无线回传与接入链路的频带切割比例,虚拟网络中SP用户的接入端资源分配问题可表示为
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{\rm{P2}}{\rm{.1:}}\mathop {\min }\limits_y - V\sum\limits_{k = 1}^K {{G_k}\left( t \right)} - \sum\limits_{k \in K} {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {{Q_{{k_{\rm{u}}}}}\left( t \right){Z_{{k_{\rm{u}}}}}\left( t \right)} } + }\\ {\sum\limits_{k = 1}^K {{D_k}\left( t \right)\left[ {{R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right]} } \end{array}\\ {\rm{s}}.\;{\rm{t}}.\;\;{C_2} \sim {C_4} \end{array} $ | (14) |
通过联合考虑目标函数和约束条件可得到对应的拉格朗日函数为
| $ \begin{array}{*{20}{c}} {L\left( {y,\lambda ,\beta } \right) = \sum\limits_{n = 0}^N {{\lambda _n}\left( {\sum\limits_{k = 1}^K {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {y_{{k_{\rm{u}}}}^n\left( t \right) - 1} } } \right)} + }\\ {\sum\limits_{n = 1}^N {{\beta _n}\left( {\sum\limits_{{k_{\rm{u}}} \in {U_n}} {y_{{k_{\rm{u}}}}^n\left( t \right)\alpha Br_{{k_{\rm{u}}}}^n\left( t \right)} - {R^n}\left( t \right)} \right)} - }\\ {\sum\limits_{k = 1}^K {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {{Q_{{k_{\rm{u}}}}}\left( t \right){Z_{{k_{\rm{u}}}}}\left( t \right)} } + }\\ {\sum\limits_{k = 1}^K {{D_k}\left( t \right)\left[ {{R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right]} - }\\ {V\sum\limits_{k = 1}^K {\left[ {{\omega _k}U\left( {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right) - {\gamma _k}G_k^\alpha \left( t \right) - {\rho _k}G_k^b\left( t \right)} \right]} } \end{array} $ | (15) |
通过KKT条件获得最优的SP用户接入频带资源调度方案:
| $ {\left[ {y_{{k_{\rm{u}}}}^n\left( t \right)} \right]^ * } = \left[ {\frac{{V{\omega _k}}}{{\ln 2}} \cdot \frac{1}{{V{\gamma _k}\alpha B + {\lambda _n} + \alpha B\chi }}} \right]_0^1 $ | (16) |
其中
| $ \chi \left[ {{\beta _n} + V{\rho _k}\frac{{\left( {1 - \alpha } \right)B}}{S} - {D_k}\left( t \right) - \frac{{{Q_{{k_{\rm{u}}}}}\left( t \right)}}{S}} \right]r_{{k_{\rm{u}}}}^n\left( t \right) $ |
同时,利用梯度法更新拉格朗日乘子, 并将更新后的值重新代入式(16)中计算,从而得到新的调度方案y.当迭代次数足够多时即可求得子问题P2.1的最优解.
4.2 回传与接入链路的频带切割子问题回传链路上的资源调度问题可表示为
| $ \begin{array}{*{20}{c}} {{\rm{P}}2.2:\mathop {\min }\limits_\alpha - V\sum\limits_{k = 1}^K {{G_k}\left( t \right)} - \sum\limits_{k \in K} {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {{Q_{{k_{\rm{u}}}}}\left( t \right){Z_{{k_{\rm{u}}}}}\left( t \right)} } + }\\ {\sum\limits_{k = 1}^K {{D_k}\left( t \right)\left[ {{R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {\sum\limits_{n = 0}^N {{y^ * }\left( t \right)\alpha Br_{{k_{\rm{u}}}}^n\left( t \right)} } } \right]} }\\ {{\rm{s}}.\;{\rm{t}}.\;\;{C_2}:\sum\limits_{{k_{\rm{u}}} \in {U_n}} {{y^ * }\left( t \right)\alpha Br_{{k_{\rm{u}}}}^n\left( t \right)} \le {R^n}\left( t \right),\forall n,n \ne 0}\\ {{C_5}:0 \le \alpha \le 1} \end{array} $ | (17) |
子问题P2.2是一个凸集上的非凸优化问题,采用基于相似度随机变异的改进型粒子群算法(IPSO-RM, improved particle swarm optimization algorithm with random mutation based on similarity)求解.
粒子m与j代中全局最优粒子g之间的相似度定义为
| $ s\left( {m,g} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\left( {d\left( {m,g} \right) < {d_{\min }}} \right.\\ 1 - {\left[ {\frac{{d\left( {m,g} \right)}}{{{d_{\max }}}}} \right]^\theta },\;\;\;\;{d_{\min }} \le d\left( {m,g} \right) < {d_{\max }}\\ 0,\;\;\;\;\;d\left( {m,g} \right) \ge {d_{\max }} \end{array} \right. $ | (18) |
其中:d(m, g)为粒子与全局最优粒子的欧氏距离,dmax和dmin为2个正常数,θ为控制参数.
同时,引入聚集度来表征粒子群的聚集程度. j代的种群聚集度为
| $ F\left( j \right) = \frac{1}{M}\sum\limits_{m = 1}^M {s\left( {m,g} \right)} $ | (19) |
其中M代表系统中粒子的数量.式(19)值越大,则种群多样性越低,相应地有更多的粒子聚集到最优粒子g的附近.倘若此时最优粒子g的位置只是局部最优点,粒子群便会失去搜索其他区域的能力,导致算法无法获得全局最优解.因此,当粒子聚集到粒子g周围时,采用一种基于相似度与聚集度随机变异的策略:
| $ \begin{array}{l} {\rm{If}}\;\;\;{x_m} \cdot {\rm{rand}}\left( \; \right) < \theta \cdot F\left( j \right)s\left( {m,g} \right)\\ {\rm{Then}}\;\;\;\;{x_m} = {\rm{random}}\left( {{x_{\min }},{x_{\max }}} \right) \end{array} $ |
其中xmin和xmax分别为粒子的最小、最大的位置.
5 仿真结果与分析考虑在500 m×500 m的物理网络覆盖区域内为3个SP提供资源共享服务,其中物理网络由1个宏基站和3个具有自回传功能的小基站构成,并将宏基站固定在区域中心处,随机部署小基站的位置和用户的位置.系统中的可用带宽为100 MHz,用户和小基站的发射功率分别为20 dBm和33 dBm,其余SP效用参数参见文献[15].对算法在T=1 000个周期内的性能进行评估,每个周期时隙长度设置为5 ms.
首先,对所提基于Lyapunov优化的算法性能进行评估. 图 3所示为SP平均总收益和时间平均队列积压与控制参数V的关系.如图所示,随着V的增加,SP平均总收益逐渐增大并趋于平稳.在Lyapunov优化中,控制参数越大则系统更倾向于优化罚函数.然而,当V增加时,时间平均队列积压近乎线性递增,这是因为系统收益与时延之间存在相互制约的关系.
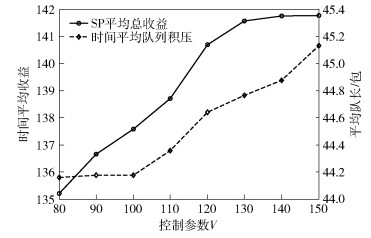
|
图 3 平均收益和平均队列积压与控制参数V的关系 |
其次,验证了所提算法在无线网络虚拟化上的性能,并在相同场景下与静态资源分配(SA-SBL, static allocation with self-backhaul link)策略和基于用户CSI的动态资源分配(CSI-DA-SBL, CSI-based dynamic allocation with self-backhaul link)策略进行对比验证.
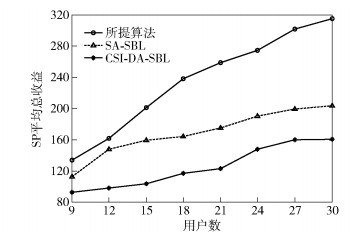
图 4显示了SP平均收益在不同接入用户数下的变化情况.随着接入用户数的增加,SP将获得更多的收入,因此SP的平均收益也呈现递增的趋势.从图中可以看出,所提算法明显优于其他2种方案,这是因为所提算法联合考虑了用户的信道质量和SP的效用,以最大化系统总收益为目标,为不同SP分配适量的虚拟频带资源.相反,SA-SBL为每个SP分配固定的资源量而忽略是否需要SP,导致资源的浪费,因此该方案中SP的收益并没有显著提升.
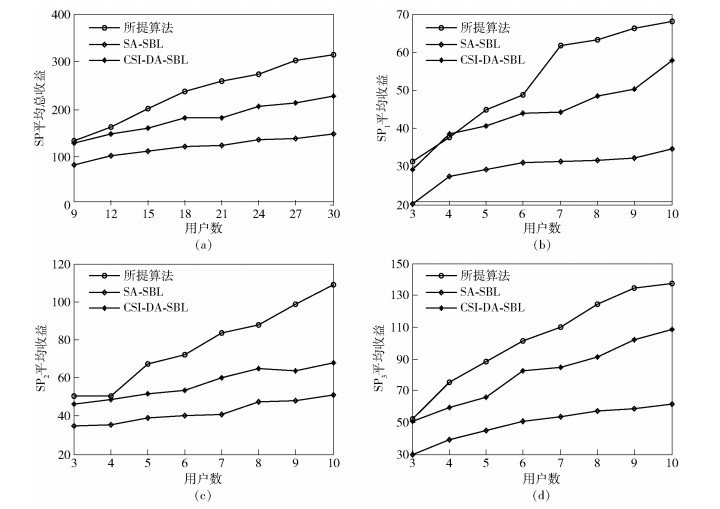
|
图 4 不同虚拟化方案的SP平均收益比较 |
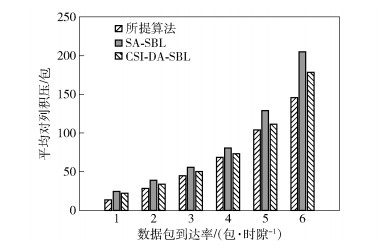
图 5描述了平均队列积压与数据包到达率的关系.对于任意的平均数据包到达率,所提的资源分配方案具有更少的队列积压.这是因为所提算法在每个时隙上结合用户的缓存状态动态地分配资源,从而保证系统内所有队列都趋于平稳,因此具有更优的时延性能.
|
图 5 不同虚拟化方案的平均对列积压比较 |
最后测试了回传机制的性能,并对比了2种回传方案,即固定频带切割比例的无线自回传机制(FBB,fixed backhaul bandwidth)和有线回传机制(WB, wired backhaul).
从图 6、图 7可以看出,所提的动态自回传机制可以为SP和InP带来更多的收益.由于FBB机制在无线回传和接入链路上采用静态配置的频带切割方式,导致自回传小基站在回传与接入容量上无法匹配,浪费了一定数量的频带资源,InP和SP的收益也将降低.尽管WB可提供较大的回传容量,但回传的成本也将增加,InP的回传收入将用于建设回传设备,因此WB机制中的SP和InP收益明显低于其他2种方案.
|
图 6 不同回传方案的SP平均收益比较 |

|
图 7 不同回传方案的InP平均效用比较 |
基于无线自回传网络提出了一种最大化SP平均总收益的虚拟资源调度方案.该方案利用商业化模型将频带资源作为收益载体,并结合自回传机制,对无线接入和小蜂窝回传带宽进行联合分配.同时,考虑到无线信道的时变特征、用户业务的随机到达以及缓存空间的局限性,利用Lyapunov优化设计了一种基于当前网络状态的实时调度算法, 最终在保证系统队列稳定性的同时有效提高了服务提供商的平均总收益.
附录1
类比不等式
| $ \max {\left\{ {Q - R + A,0} \right\}^2} \le {Q^2} + {R^2} + {A^2} - 2Q\left( {R - A} \right) $ |
则式(4)的平方应满足
| $ \begin{array}{*{20}{c}} {{Q_{{k_{\rm{u}}}}}{{\left( {t + 1} \right)}^2} \le {Q_{{k_{\rm{u}}}}}{{\left( t \right)}^2} + {A_{{k_{\rm{u}}}}}{{\left( t \right)}^2} + {Z_{{k_{\rm{u}}}}}{{\left( t \right)}^2} - }\\ {2{Q_{{k_{\rm{u}}}}}\left( t \right)\left[ {{Z_{{k_{\rm{u}}}}}\left( t \right) - {A_{{k_{\rm{u}}}}}\left( t \right)} \right]} \end{array} $ | (20) |
将式(20)对所有用户进行累积求和,可得到不等式:
| $ \begin{array}{*{20}{c}} {\sum\limits_{k = 1}^K {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {\frac{{{Q_{{k_{\rm{u}}}}}{{\left( {t + 1} \right)}^2} - {Q_{{k_{\rm{u}}}}}{{\left( t \right)}^2}}}{2}} } \le }\\ {\sum\limits_{k = 1}^K {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {\frac{{{A_{{k_{\rm{u}}}}}{{\left( t \right)}^2} - {Z_{{k_{\rm{u}}}}}{{\left( t \right)}^2}}}{2}} } - }\\ {\sum\limits_{k = 1}^K {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {{Q_{{k_{\rm{u}}}}}\left( t \right)\left[ {{Z_{{k_{\rm{u}}}}}\left( t \right) - {A_{{k_{\rm{u}}}}}\left( t \right)} \right]} } } \end{array} $ | (21) |
同理,对于虚拟SP速率队列,可得
| $ \begin{array}{*{20}{c}} {\sum\limits_{k = 1}^K {\frac{{{D_k}{{\left( {t + 1} \right)}^2} - {D_k}{{\left( t \right)}^2}}}{2}} \le }\\ {\sum\limits_{k = 1}^K {\frac{{R_k^2 + {{\left[ {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right]}^2}}}{2}} + }\\ {\sum\limits_{k = 1}^K {{D_k}\left( t \right)\left[ {{R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right]} } \end{array} $ | (22) |
将不等式(21)、式(22)代入式(11),可以得到
| $ \begin{array}{*{20}{c}} {\Delta \left( {\mathit{\Omega }\left( t \right)} \right) - VE\left\{ {\sum\limits_{k = 1}^K {{G_k}\left( t \right)\left| {\mathit{\Omega }\left( t \right)} \right.} } \right\} \le }\\ {\zeta + E\left\{ {\sum\limits_{k \in K} {{D_k}\left( t \right)\left[ {{R_k} - \sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right]\left| {\mathit{\Omega }\left( t \right)} \right.} } \right\} + }\\ {E\left\{ {\sum\limits_{k \in K} {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {\left\{ {{Q_{{k_{\rm{u}}}}}\left( t \right)\left[ {{A_{{k_{\rm{u}}}}}\left( t \right) - {Z_{{k_{\rm{u}}}}}\left( t \right)} \right]\left| {\mathit{\Omega }\left( t \right)} \right.} \right\}} } } \right\} - }\\ {VE\left\{ {\sum\limits_{k = 1}^K {{G_k}\left( t \right)\left| {\mathit{\Omega }\left( t \right)} \right.} } \right\}} \end{array} $ |
其中
| $ \begin{array}{*{20}{c}} {\zeta \ge \frac{1}{2}E\left\{ {\sum\limits_{k = 1}^K {\sum\limits_{{k_{\rm{u}}} = 1}^{{U_k}} {\frac{{{A_{{k_{\rm{u}}}}}{{\left( t \right)}^2} + {Z_{{k_{\rm{u}}}}}{{\left( t \right)}^2}}}{2}} } + } \right.}\\ {\left. {\sum\limits_{k = 1}^K {\left[ {R_k^2 + {{\left( {\sum\limits_{{k_{\rm{u}}} \in {U_k}} {{R_{{k_{\rm{u}}}}}\left( t \right)} } \right)}^2}} \right]\mathit{\Omega }\left( t \right)} } \right\}} \end{array} $ |
| [1] | Agyapong P K, Iwamura M, Staehle D, et al. Design considerations for a 5G network architecture[J]. IEEE Communications Magazine, 2014, 52(11): 65–75. doi: 10.1109/MCOM.2014.6957145 |
| [2] | Rost P, Berberana I, Maeder A, et al. Benefits and challenges of virtualization in 5G radio access networks[J]. IEEE Communications Magazine, 2015, 53(12): 75–82. doi: 10.1109/MCOM.2015.7355588 |
| [3] | Rahman M M, Despins C, Affers S. Design optimization of wireless access virtualization based on cost & QoS trade-off utility maximization[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 6146–6162. doi: 10.1109/TWC.2016.2580505 |
| [4] | Liang C, YU F R. Wireless network virtualization:a survey, some research issues and challenges[J]. IEEE Communications Surveys & Tutorials, 2014, 17(1): 358–380. |
| [5] | Richart M, Baliosian J, Serrat J, et al. Resource slicing in virtual wireless networks:a survey[J]. IEEE Transactions on Network & Service Management, 2016, 13(3): 462–476. |
| [6] | Kamel M I, Long B L, and Girard A. LTE wireless network virtualization: dynamic slicing via flexible scheduling[C]//IEEE Vehicular Technology Conference(VTC). Vancouver: IEEE, 2014: 1-5. |
| [7] | Parsaeefard S, Jumba V, Derakhshani M, et al. Joint resource provisioning and admission control in wireless virtualized networks[C]//IEEE Wireless Communications and Networking Conference(WCNC). New Orleans: IEEE, 2015: 2020-2025. |
| [8] | Zhu K, Hpssain E. Virtualization of 5G cellular networks as a hierarchical combinatorial auction[J]. IEEE Transactions on Mobile Computing, 2016, 15(10): 2640–2654. doi: 10.1109/TMC.2015.2506578 |
| [9] | Gao L, Li P, Pan Z, et al. Virtualization framework and VCG based resource block allocation scheme for LTE virtualization[C]//IEEE Vehicular Technology Conference(VTC). Nanjing: IEEE, 2016: 1-6. |
| [10] | Wang N, Hossain E, Bhargava V K. Backhauling 5G small cells:a radio resource management perspective[J]. IEEE Wireless Communications, 2015, 22(5): 41–49. doi: 10.1109/MWC.2015.7306536 |
| [11] | Li B, Zhu D, Liang P. Small cell in-band wireless backhaul in massive MIMO systems:a cooperation of next-generation techniques[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 7057–7069. doi: 10.1109/TWC.2015.2464299 |
| [12] |
唐伦, 梁荣, 陈婉, 等. 密集网络下基于self-backhaul感知的用户接入负载均衡算法研究[J]. 北京邮电大学学报, 2017, 40(4): 60–67.
Tang Lun, Liang Rong, Chen Wan, et al. User association load balancing algorithm based on self-backhaul aware in dense networks[J]. Journal of Beijing University of Posts and Telecommunication, 2017, 40(4): 60–67. |
| [13] | Xu Z, Min S, Yan S, et al. Energy efficiency and delay tradeoff for time-varying and interference-free wireless networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(11): 5921–5931. doi: 10.1109/TWC.2014.2355206 |
| [14] | Liu Y, Lu L, Li G, et al. Joint user association and spectrum allocation for small cell networks with wireless backhauls[J]. IEEE Wireless Communications Letters, 2016, 5(5): 496–499. doi: 10.1109/LWC.2016.2593465 |
| [15] | Leanh T, Tran N H, Ngo D T, et al. Resource allocation for virtualized wireless networks with backhaul constraints[J]. IEEE Communications Letters, 2017, 21(1): 148–151. doi: 10.1109/LCOMM.2016.2617307 |


