2. 无锡北邮感知技术产业研究院有限公司, 江苏 无锡 214135
为了给用户提供更好的位置服务,提出了一种位置社交网络中融入时空上下文信息的混合个性化兴趣点推荐模型.在空间上,对用户签到进行层次聚类,对各聚类内二维核密度估计的结果取平均.在时间上,利用用户签到的时间信息、签到的位置信息及社交网络构建转移矩阵,运行改进图的随机游走模型.混合模型融合时空上下文信息做推荐.在真实数据集上的实验结果表明,无论在标准推荐场景还是冷启动场景下,混合推荐模型的准确率和召回率性能均优于基准方法.
2. Institute of Sensing Technology and Business, Beijing University of Posts and Telecommunications, Jiangsu Wuxi 214135, China
A personalized hybrid point-of-interest recommendation with spatio-temporal context awareness was proposed to provide users in location-based social networks with superior service. Spatially, two-dimension kernel density estimation was performed for each cluster of check-ins derived by hierarchical clustering and averaged. Meanwhile, random walk on graph was iterated on transition matrices generated from sequence information, location information and social network. The hybrid model combines spatio-temporal context above for recommendation. Experiment on real-world location-based social network(LBSN) datasets demonstrates that the performance metrics of precision and recall of the hybrid recommendation model is superior to other baseline techniques in both standard recommendation scene and cold-start scene.
智能手机等移动终端的普及和定位技术的提高,可以准确地获得位置信息,催生了基于位置的社交网络(LBSN,location-based social network)的发展.以Foursquare为例,截至2017年5月,超过0.5亿用户在9 300万个地点进行了100亿次签到,并且以900万次/d签到的速度增加.兴趣点(POI,point-of-interest)推荐就是利用历史签到位置、社交网络等上下文要素来给用户推荐令其感兴趣的位置.
个性化和冷启动问题是兴趣点推荐面临的重要挑战.当新用户进入推荐系统时,往往只有1~5个签到,使得推荐系统不能从有限的知识中挖掘出用户兴趣,从而引入了用户冷启动问题.另外,历史签到记录足够丰富的用户,其偏好容易趋向于该用户所在区域内的热门兴趣点,而那些分布偏远的兴趣点会被淹没其中,导致推荐缺乏个性化.
1 相关工作随着基于位置社交网络的蓬勃发展,基于用户签到的位置推荐引起了研究者广泛关注.为了提高推荐精度,徐雅斌等[1]采用结合兴趣点的语义特征和时间遗忘因子;王晓军[2]引入了用户特征,提高了用户相似度的精度.这些模型仅用单一上下文进行协同过滤,冷启动场景下效果不佳.为了丰富上下文信息,Cho等[3]建立了居住区和工作区的两中心高斯混合模型,提出周期性行为模式;Ye等[4]整合了用户偏好、社交影响力和地理影响力,但都人为地赋予了用户空间先验分布.鉴于统一的先验分布会削弱个性化的情况,Zhang等[5]使用一维核密度估计方法,引入了空间个性化要素,然而单一距离度量损失了签到兴趣点的方位信息;Lichman等[6]把城市级别的二维核密度估计与个人层面的估计融合起来,缓解了冷启动问题,但推荐结果趋向于热门区域.为了提高用户的个性化推荐,其他隐藏上下文信息也被充分挖掘;Li等[7]挖掘潜在好友关系,并进一步整合到隐式评分矩阵中进行矩阵分解,但该方法没有考虑序列顺序;He等[8]利用3阶张量建模连续签到序列,挖掘了用户的隐藏行为模式,但模型没有考虑用户的交互.
以上方法对位置信息的挖掘都将区域内的整体分布作为个体分布的先验,导致用户的个性化往往集中于频繁签到的兴趣点,并且没有考虑兴趣点的个性化方位信息和访问顺序,推荐效果不佳.笔者提出了一种混合推荐模型(GTU,geographical and temporal model with user interaction),融合了时空上下文要素及用户之间的交互,使用层次聚类发掘小众兴趣区域,并在区域内部使用二维核密度估计获得用户偏好,满足了用户个性化需求.同时,随机游走作用于用户和位置两类结点,并引入签到的时间序列影响,可以缓解冷启动对推荐系统的影响.
2 个性化混合推荐模型 2.1 位置社交网络的构成位置社交网络由用户结点集合U={u1, u2, …, uM}和位置结点集合L={l1, l2, …, lN}2种结点集合构成,M和N分别表示用户总数和位置总数,其中每个位置l对应一个位置向量l=⟨e, z⟩,表示该位置的经纬度坐标,所有位置向量的集合构成空间矩阵G.签到集合S={sji=⟨lji, tji⟩|1≤i≤M, 1≤j≤ni},其中sji=⟨lji, tji⟩表示ui第j次签到发生于时间tji和位置lji,ni是ui的签到次数.社交网络F={Fi|1≤i≤M},其中Fi⊆U是ui的好友集合. 2个公开的位置社交网络Brightkite[3]和Foursquare[9]被用于分析和实验.
2.2 空间分布建模 2.2.1 空间分布分析用户的签到序列通常呈簇分布,并且各不相同,这反映了用户对兴趣点的偏好因人而异,因此考虑建立个性化空间分布模型.而核密度估计优良的非参数估计特性恰好可以对空间分布进行个性化建模.
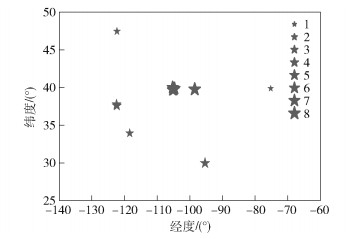
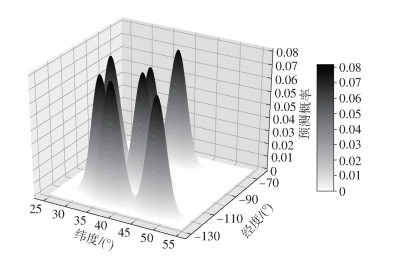
为了使签到较稀疏区域内的位置也能够被推荐给用户,采用先聚类再做类内核密度估计的方法. 图 1所示为来自Brightkite数据集的真实用户经过层次聚类之后的空间概率分布情况.可以看出,用户签到呈簇分布,每个簇代表一个活动区域,簇的大小不一. 图 2所示为该用户在每个区域内进行核密度估计的结果,签到概率在各聚类簇中相对平衡.
|
图 1 一个用户的签到在平面空间上呈簇分布 |
|
图 2 一个用户进行聚类核密度估计 |
1) 对用户的历史签到位置进行层次聚类.层次聚类在空间上按照物理距离把签到地点分成几个大小不一的簇,簇间距离较远,簇内位置彼此较近.用户ui的签到位置经过层次聚类产生Ti个子类Ci={c1i, c2i, …, cTii},其中cki⊆Gi表示ui的第k个子类,由该用户相应的签到位置向量构成.
2) 按用户生成核密度估计模型.核密度估计的样本取自每个用户签到的经纬度分布,采用二维估计模型,用户ui的第k个聚类cki的核密度估计为
| $ f_k^i\left( \mathit{\boldsymbol{l}} \right) = \frac{1}{{\left| {c_k^i} \right|}}\sum\limits_{\mathit{\boldsymbol{l'}} \in c_k^i} {{K_h}\left( {\mathit{\boldsymbol{l}},\mathit{\boldsymbol{l'}}} \right)} $ | (1) |
其中:l为待推荐兴趣点的位置向量,l′为用户历史签到兴趣点的位置向量,Kh(·, ·)为核函数.考虑到不同签到的方位信息,核函数采用二维高斯函数,表示为
| $ \left. \begin{array}{l} {K_h}\left( {\mathit{\boldsymbol{l}},\mathit{\boldsymbol{l'}}} \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}h}}\exp \left( { - \frac{1}{2}\left( {\mathit{\boldsymbol{l}} - \mathit{\boldsymbol{l'}}} \right)\mathit{\Sigma }_h^{ - 1}{{\left( {\mathit{\boldsymbol{l}} - \mathit{\boldsymbol{l'}}} \right)}^{\rm{T}}}} \right)\\ {\mathit{\Sigma }_h} = \left( {\begin{array}{*{20}{c}} h&0\\ 0&h \end{array}} \right) \end{array} \right\} $ | (2) |
其中:h为带宽,Σh为协方差矩阵.
3) 预测新位置的概率.根据步骤2)得到的类内核密度估计模型,每个新位置的预测概率可以为
| $ {p_i}\left( {l\left| {{\mathit{\boldsymbol{G}}_i}} \right.} \right) = \frac{1}{{{T_i}}}\sum\limits_{k = 1}^{{T_i}} {f_k^i\left( \mathit{\boldsymbol{l}} \right)} $ | (3) |
其中:Gi为用户ui历史签到的二维空间矩阵,l为待推荐的新位置,Ti为ui的聚类数目.根据式(3)计算出用户在所有新位置上的签到概率,并且为用户推荐k个最大预测概率的位置pi(l|Gi).
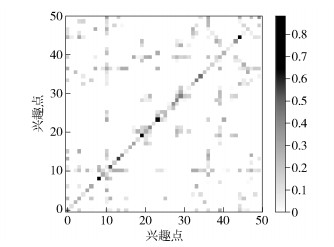
2.3 时间序列建模 2.3.1 时间序列分析时间序列表现为用户对于偏好位置的访问具有位置依赖和时间依赖.位置依赖指同一个用户访问的任意2个地点都隐含相同的特征,存在依赖.在Brightkite和Foursquare数据集中,用户平均重复签到率分别是61.14%和19.78%,说明用户会重复访问感兴趣的POI. 图 3为Brightkite中50个POI的转移概率热图,图中每个位置转移到自身的概率最高,说明相同用户的兴趣在一段时间会保持在同一个兴趣点.更广泛地,相同用户一段时间访问的多个兴趣点都体现了隐藏的用户特征,这些兴趣点具有位置依赖,即位置交互.而且用户访问2个位置的顺序决定了位置依赖的强度,位置依赖的序列性.用户的偏好随时间而漂移,即位置依赖的时间衰减性.此外,用户还通过社交网络传递共同的兴趣点偏好.
|
图 3 50个POI的转移概率矩阵 |
位置交互和用户交互是同构交互关系.用户签到行为连接了用户结点和位置结点,即用户位置交互关系,偏好信息在用户和位置之间转移属于异构关系.提出的迭代增强算法利用随机游走多轮迭代不断增强这两类结点,使每个结点收敛于一个稳定的概率,具有较高稳定概率的位置结点即可被推荐给用户.
2.3.2 构建转移矩阵基于以上分析,用户偏好信息不仅来自于同构结点的交互,还来自于异构结点的交互.偏好转移关系可以采用3个矩阵表示:用户交互矩阵、位置交互矩阵和用户位置交互矩阵.
1) 用户交互矩阵
在社交网络中,如果用户建立了连接,他们之间就存在好友关系,全部好友关系构成了用户社交网络图,其邻接矩阵表示为
| $ \mathit{\boldsymbol{A}} = {\left( {{a_{ij}}} \right)_{M \times M}} $ | (4) |
好友之间的连接强度aij用Jaccard相似度衡量.
| $ {a_{ij}} = \frac{{\left| {F\left( {{u_i}} \right) \cap F\left( {{u_j}} \right)} \right|}}{{\left| {F\left( {{u_i}} \right) \cup F\left( {{u_j}} \right)} \right|}} $ | (5) |
其中:F(ui)表示ui的好友集合,而非好友之间的连接强度aij为零.
2) 用户位置交互矩阵
用户位置交互矩阵为
| $ \mathit{\boldsymbol{B}} = {\left( {{b_{ij}}} \right)_{M \times N}} $ | (6) |
其中bij表示用户ui在位置lj的签到频率.行向量表示每个用户在N的位置上的归一化签到频率,列向量表示每个位置被M个用户访问的频率.
3) 位置交互矩阵
位置交互矩阵反映了位置之间的依赖关系,以N阶方阵表示为
| $ \mathit{\boldsymbol{C}} = {\left( {{w_{ij}}} \right)_{N \times N}} $ | (7) |
正如2.3.1节的描述,2个位置共现于同一用户的签到中,便存在潜在的序列依赖,并且位置依赖具有序列性.对于每个用户的任意2次签到si和sj,ti < tj,wij表示位置li到lj的转移概率,α为前向转移系数.由于位置依赖的时间衰减性,转移概率还受时间间隔影响,所以wij按式(8)更新
| $ \left. \begin{array}{l} {w_{ji}} = {w_{ji}} + \frac{\alpha }{{\left| {{t_i} - {t_j}} \right|}}\\ {w_{ij}} = {w_{ij}} + \frac{1}{{\left| {{t_i} - {t_j}} \right|}} \end{array} \right\} $ | (8) |
其中:α∈[0, 1],|ti-tj|表示签到的时间间隔,以天为单位,wji和wij均以零为初值.
2.3.3 异构随机游走异构随机游走模型融合了兴趣点依赖关系和用户社交网络,使其偏好信息通过用户和位置之间3种不同的转移关系不断传递.
使用列向量ui和vi分别表示ui与用户稳态偏好相似度和ui与位置的稳态访问概率.异构随机游走模型对每个用户迭代所有结点的稳态概率.根据2.3.1的分析,用户稳态概率可以从A和B得到;位置稳态结点可以从C和BT得到.所以,各结点的稳态概率来自于同类结点的转化和异构结点的转移,如式(9)所示,每一类结点以小概率β回归起始状态.
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{u}}_i} = \left( {1 - \beta } \right)\left( {a\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{u}}_i} + b\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{v}}_i}} \right) + \beta {\mathit{\boldsymbol{x}}_i}\\ {\mathit{\boldsymbol{v}}_i} = \left( {1 - \beta } \right)\left( {a\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{v}}_i} + b{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{u}}_i}} \right) + \beta {\mathit{\boldsymbol{y}}_i} \end{array} \right\} $ | (9) |
其中:xi、yi和β∈[0, 1]分别表示用户ui的用户重启向量、位置重启向量和重启概率,表示ui随机游走的过程中会有一个小概率回到初始状态;用户重启向量xi是当前用户的好友,位置重启向量yi是当前用户的历史访问位置;a和b表示同构结点和异构结点对最终偏好信息权重的相对贡献度,并且a+b=1;各交互矩阵分别按列归一化;迭代过程通常停止于最大迭代次数或者稳态向量收敛. ui经过多轮随机游走生成的N维位置向量vi即为该用户访问各位置的长期概率,以pi(l|L, U)表示,l是待推荐的新位置,L和U分别是位置结点集合和用户结点集合.
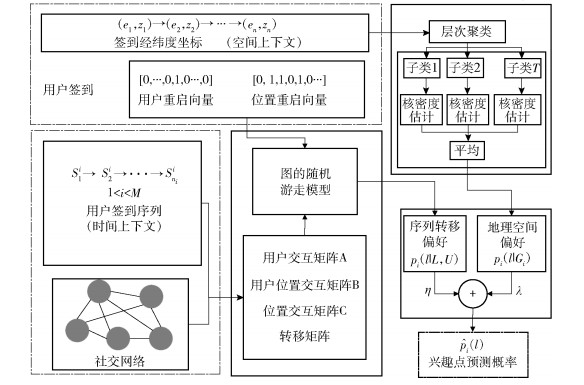
2.4 模型融合以上模型挖掘了签到行为的空间分布和时间序列分布,通过加法规则[4]融合各子模型的输出,图 4所示为提出的混合推荐模型的框架.空间分布模型先对用户签到进行层次聚类,再进行类内核密度估计,然后平均各类的估计结果.时间序列模型使用户结点和位置结点在LBSN的3种交互关系之间转移并相互增强,最终位置结点的稳态概率趋向于用户的偏好兴趣点分布.
|
图 4 混合推荐模型 |
混合模型通过线性加权的方式给予各上下文以不同的权重,采用加法规则[4]融合不同子模型的结果.综上所述,混合模型的最终输出概率为
| $ {{\hat p}_i}\left( l \right) = \lambda {p_i}\left( {l\left| {{\mathit{\boldsymbol{G}}_i}} \right.} \right) + \eta {p_i}\left( {l\left| {L,U} \right.} \right) $ | (10) |
其中λ+η=1用来均衡不同上下文对于推荐模型预测概率的贡献度.
3 实验及分析 3.1 数据集和参数设置为了比较不同模型在个性化推荐和冷启动推荐场景下的推荐质量,在2个数据集上进行了实验. Brightkite数据集平均签到数为71.71,用作个性化位置推荐. Foursquare数据集平均签到数为5.21,用作冷启动推荐.每个数据集按照用户的签到时间依8:2分为训练集和测试集.评价指标采用准确率和召回率.数据集统计结果见表 1.
|
|
表 1 数据集统计 |
实验中参数α、β、a、b分别设置为0.5、0.1、0.5、0.5. Brightkite中λ、η分别设置为0.5、0.5. Foursquare中λ、η分别设置为0.4、0.6.
3.2 基准方法为了说明提出混合推荐系统的有效性,GTU模型与以下几种推荐模型做比较:
1) 概率矩阵分解模型(PMF, probability matrix factorization)把用户的签到看作评分,加入正则项;
2) USG[4]综合考虑了用户、社交和地理位置3种因素的混合推荐系统;
3) ASMF[7]挖掘用户的潜在好友,用幂函数衡量位置之间的相似度,最小化平方误差损失函数;
4) iGSLR[5]结合贝叶斯准则应用一维核密度估计,为每个用户生成个性化空间模型.
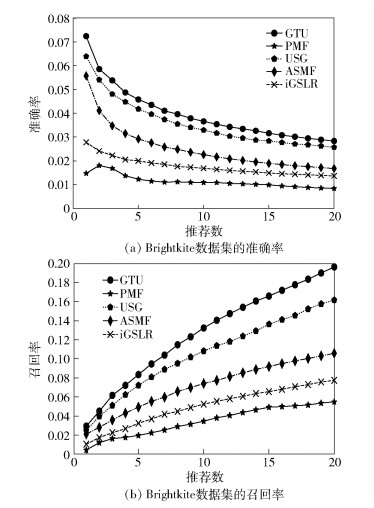
3.3 实验结果及分析 3.3.1 个性化推荐Brightkite数据集用于比较不同模型对于个性化兴趣点推荐的准确率和召回率关于推荐位置数目的推荐质量(见图 5).在所有推荐数目下,GTU模型的推荐准确率和召回率都高于其他模型,PMF的效果最差.随着推荐数目的增加,所有模型的召回率都有所上升,但是GTU的召回率提升相比于其他模型更为显著.
|
图 5 Brightkite上不同模型的推荐质量 |
GTU和USG属于混合推荐模型,能够从不同角度充分挖掘出用户的偏好,故其准确率与召回率都优于其他非混合推荐系统. GTU对每个用户分别建立个性化的空间模型,USG和ASMF用幂函数拟合距离分布,所以GTU的效果比USG好. PMF仅仅考虑了用户可观察的签到,而没有考虑社交关系和地理空间要素,在兴趣点推荐的稀疏性环境下,其性能自然比较差. ASMF融合了社交关系和位置距离度量,弥补了PMF的不足,但其没有考虑位置签到顺序,因此GTU在准确率和召回率上高于ASMF. iGSLR使用一维核密度估计损失了位置之间的方位信息,导致预测精度较GTU有大的衰减.另外,GTU比起其他模型,考虑了位置之间的转移概率,这种转移信息可以反映出兴趣点的隐含特征,因而GTU的准确率与召回率都是最佳.
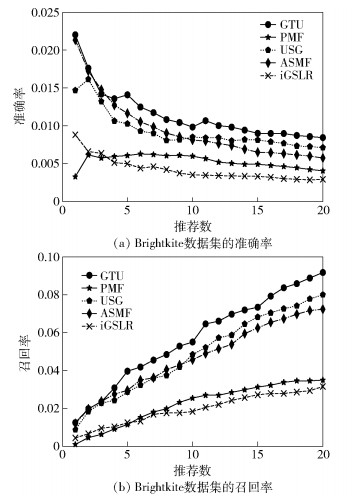
3.3.2 冷启动推荐采用Foursquare数据集来评价不同模型在冷启动场景下的推荐性能. 图 6所示为GTU与其他模型在Foursquare数据集上的性能比较.与图 5相比,准确率和召回率都有所下降,因为数据集的样本量减少,同时每个用户的签到都很少.因为小样本情况下,噪声对实验结果的影响力被放大,所以在推荐个数少于5个的情况下,评价指标的波动比较大.
|
图 6 Foursquare上不同模型的推荐质量 |
GTU的全用户随机游走模型通过社交网络把用户与其他非好友用户联系起来,针对冷启动用户有很好的表现. iGSLR需要较多的用户签到数据,在冷启动场景下用户签到数据不足,因此其性能严重下降,甚至低于PMF.而GTU的性能仍旧优于USG和ASMF,这主要得益于其随机游走模型把所有用户和位置的影响都考虑进去,对于冷启动用户较少的签到表现比较好.
4 结束语用户个性化是基于位置社交网络推荐系统的基本要求,同时冷启动问题也是兴趣点推荐系统面临的挑战,针对这2个问题提出了混合推荐模型.首先,层次核密度估计模型为用户建立个性化的空间分布模型;然后,考虑用户与位置间的3种交互关系,利用随机游走模型得到位置稳态概率;最后使用加法规则进一步融合了不同模型的结果.通过2个真实数据集模拟个性化和冷启动推荐场景,与现有个性化推荐方法相比,混合推荐模型GTU的准确率和召回率最优. GTU模型结合了签到数据的空间属性和时间属性,并依赖数据集分配不同的权重,但更具个性化的权重分配原则应是依赖于个人的;提出的模型没有考虑商家的描述信息和用户的评论信息.因此,下一步工作将围绕时空属性的个人影响力因子和签到行为的文本语义特征来继续完善推荐模型.
| [1] |
徐雅斌, 孙晓晨. 位置社交网络的个性化位置推荐[J]. 北京邮电大学学报, 2015, 38(5): 118–124.
Xu Yabin, Sun Xiaochen. Individual location recommendation for location-based social network[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(5): 118–124. |
| [2] |
王晓军. 推荐系统中分布式混合协同过滤方法[J]. 北京邮电大学学报, 2016, 39(2): 25–29.
Wang Xiaojun. A distributed hybrid collaborative filtering method in recommender systems[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(2): 25–29. |
| [3] | Cho E, Myers S A, Leskovec J. Friendship and mobility: user movement in location-based social networks[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego: ACM, 2011: 1082-1090. |
| [4] | Ye Mao, Yin Peifeng, Lee W C, et al. Exploiting geographical influence for collaborative point-of-interest recommendation[C]//Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval. Beijing: ACM, 2011: 325-334. |
| [5] | Zhang Jiadong, Chow C. iGSLR: personalized geo-social location recommendation: a kernel density estimation approach[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Orlando: ACM, 2013: 334-343. |
| [6] | Lichman M, Smyth P. Modeling human location data with mixtures of kernel densities[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014: 35-44. |
| [7] | Li Huayu, Ge Yong, Hong Richang, et al. Point-of-interest recommendations: learning potential check-ins from friends[C]//Proceedings of the 22th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016: 975-984. |
| [8] | He Jing, Li Xin, Liao Lejian et al. Inferring a personalized next point-of-interest recommendation model with latent behavior patterns[C]//Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix: AAAI Press, 2016: 137-143. |
| [9] | Bao Jie, Zheng Yu, Mokbel M F. Location-based and preference-aware recommendation using sparse geo-social networking data[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems. California: ACM, 2012: 199-208. |


