2. 解放军理工大学 通信工程学院, 南京 210007;
3. 中国电子科技集团第二十八研究所, 南京 210007
无人机(UAV)机载网络的性能紧密地依赖于所釆用的移动模型中节点的移动方式,移动模型及其参数的选择也对其仿真结果具有重要意义.在三维高斯马尔可夫移动模型(3D-GMM)的基础上增加了基于访问密度的移动牵引,提出了一种基于访问密度的新型三维高斯半马尔可夫移动模型(3D-VDGMM).仿真实验表明3D-VDGMM能够很好地对UAV的移动进行模拟,且相比于3D-GMM能够有更高的事件捕获率.
2. Communication Engineering, PLA University of Science and Technology, Nanjing 210007, China;
3. The 28th Research Institute of China Electronic Technology Group Corporation, Nanjing 210007, China
The network performance of unmanned aerial vehicle(UAV) airborne is closely relied on the movement of the mobile nodes which is decided by the mobility mode. And the selection of mobility model and its parameters is of great significance to the simulation results. Based on the three-dimensional Gauss Markov mobility model (3D-GMM), this paper expands GM by using visit density, and proposes a new three-dimensional Gauss markov mobility model based on visit density (3D-VDGMM). The results show that 3D-VDGMM can simulate the movement of UAVs well and have higher event capture rate compared to 3D-GMM.
近年来,以无线Ad hoc网络为基础的机载网在航空通信领域发挥了重大作用.无人机(UAV,unmanned aerial vehicle)机载网络在空中目标监控追踪、空地态势感知交互、无人机自动防撞、空海陆协同作战、城市应急求援等领域发挥了至关重要的作用[1].一个可靠、高效、实时的UAV机载网络必须具备科学灵活的移动模型,以应对UAV机载网络所面临的事件态势捕捉、链路变化频繁、环境复杂多变等挑战.由于UAV节点高速运动的特殊性,传统的无线Ad hoc网络移动模型并不能直接适用于UAV机载网络[2].为此,Broyles等[3]针对机载网络的高动态性,设计实现三维机载网络高斯马尔可夫移动模型(3D-GMM, 3D Gauss-semi-Markov mobility). Rohrer等[4]在3D-GMM的基础上增加了效能评估. Zheng等[5]提出了一种三维平滑高斯半马尔可夫移动模型,在模型中增加了高斯扰动.何等[6]受鱼群启发,分析了节点不同状态之间的转换方式,设计了3D-NMM (3D semi-random node mobility model), 实现了对监测区域目标事件的有效覆盖.针对以上问题,通过在高斯模型中引入访问密度因素,改进了3D-GMM模型,提出了基于访问密度的三维高斯半马尔科夫移动模型(3D-VDGMM,3D visit-density gauss-semi-markov mobility).
1 问题描述和模型定义模拟UAV网络场景要准确地分析无线信号的传输,需要确切地知道移动节点的地理位置,同时UAV的移动模式直接关系到拓扑结构的变化,影响整个网络的吞吐量、传输延迟、路由有效性等指标的测量,由于实地测试面临不易控制、危险性大、不可再现等缺点和困难,对于新应用和新协议的验证主要通过模拟仿真技术完成,所以需要一个UAV的移动模型以模拟现实的UAV移动.
综合现有移动模型的优劣性,提出的模型具有以下3个特点:1) 贴近现实节点的运动为平滑运动,速率和方向具有相关性;2) 模型参数可控性强,可以独立进行调控;3) 节点移动模型为混合移动模型,即受时间、空间、地理的影响.
在目标监测区域W中,将UAV网络搜索过程抽象为一个网络G,其中定义:
网络中存在着UAV集合U={u1, u2, …, un},n为UAV的数量;
事件集为T={t1, t2, …, tk},k为事件随机出现的总数;
把网络G划分为一个个的小正方体,每个节点的监测范围为27个立方体方格,节点处于立方体中心位置.
UAV节点根据当前监测范围(27个方格)中观测到的事件和节点为依据进行移动的相关判断.
定义1(时间因素) 节点当前时刻的移动受上一时刻节点移动的影响.
定义2(空间因素) 节点受周围节点、事件的影响.
定义3(地理因素) 节点所处位置受地理环境的限制,如:UAV存在最低飞行高度等.
假设1 不考虑能耗,只针对UAV节点是如何移动的进行相关研究.
假设2 无法获知区域内历史出现的事件数和历史访问过的节点数.该假设为了使移动模型更加贴近实际,在实际应用中让UAV记录历史信息是困难的.
假设3 UAV在执行任务过程中,不会发生失效.
2 基于访问密度的3D移动模型 2.1 访问密度在机载网络中,能否对目标事件进行实时、快速、高效的监测和感知,决定了一个移动模型性能的优劣.而某一区域目标事件出现的个数,其周围节点的数量,以及其他节点的移动状态等因素都较大影响了移动模型的性能.
因此,在考虑的3D方格型网络模型中,首先对事件及其周围节点数量进行了分析.其中,事件按照一定的规律在不同的方格中随机产生,无人机按照移动模型在网络区域内移动.对于任意方格Si, j, k,其事件密度de等于该方格中当前时刻的事件总数,无人机密度du等于当前时刻该方格内的无人机数量.
定义访问密度为
| ${d_{\rm{v}}} = \frac{{{d_{\rm{e}}}}}{{\left( {1 + {d_{\rm{u}}}} \right)}}$ | (1) |
访问密度的大小决定了当前方格对无人机的需求,当该方格内的事件密度较大而当前无人机数量较少时,表明该方格对无人机的访问需求较大.
2.2 3D-VDGMM移动模型3D-GMM移动模型将二维马尔可夫模型扩展到三维,其三维速度向量表示为
| $\left. \begin{array}{l} {x_n} = \alpha {x_{n - 1}} + \left( {1 - \alpha } \right)\bar x + \sqrt {\left( {1 - {\alpha ^2}} \right)} {x_x}_{_{n - 1}}\\ {y_n} = \alpha {y_{n - 1}} + \left( {1 - \alpha } \right)\bar y + \sqrt {\left( {1 - {\alpha ^2}} \right)} {y_x}_{_{n - 1}}\\ {z_n} = \alpha {z_{n - 1}} + \left( {1 - \alpha } \right)\bar z + \sqrt {\left( {1 - {\alpha ^2}} \right)} {z_x}_{_{n - 1}} \end{array} \right\}$ | (2) |
其中:α为调整参数;xn-1、yn-1、zn-1分别为当前时刻的三维坐标值;x、y、z分别为节点在3个方向上的平均移动距离;xxn-1、yxn-1、zxn-1分别为高斯分布产生的随机变量,用来对节点的移动速度和方向增加移动的随机性.
在3D-GMM模型中,节点仅仅按照模型的定义进行移动,没有考虑环境等其他因素可能对移动产生的影响,因此基于事件的感知和捕获对该模型的高斯移动过程进行了改进,将访问密度因素引入高斯模型,使节点的移动在具有高斯特性的同时还具有事件趋向性.改进后的三维速度向量表示为
| $\left. \begin{array}{l} {x_n} = \alpha {x_{n - 1}} + \left( {1 - \alpha } \right)\bar x + \sqrt {\left( {1 - {\alpha ^2}} \right)} {\left( { - 1} \right)^{{\beta _x}}}\left| {{x_x}_{_{n - 1},{\gamma _x}}} \right|\\ {x_n} = \alpha {y_{n - 1}} + \left( {1 - \alpha } \right)\bar y + \sqrt {\left( {1 - {\alpha ^2}} \right)} {\left( { - 1} \right)^{{\beta _y}}}\left| {{y_x}_{_{n - 1},{\gamma _x}}} \right|\\ {z_n} = \alpha {z_{n - 1}} + \left( {1 - \alpha } \right)\bar z + \sqrt {\left( {1 - {\alpha ^2}} \right)} - {\left( { - 1} \right)^{{\beta _z}}}\left| {{z_x}_{_{n - 1},{\gamma _x}}} \right| \end{array} \right\}$ | (3) |
| ${\beta _{x,y,z}} = \left\{ \begin{array}{l} 0,{d_{x + ,y + ,z + }} \ge {d_{x - ,y - ,z - }}\\ 1,{d_{x - ,y - ,z - }} > {d_{x + ,y + ,z + }} \end{array} \right.$ | (4a) |
| ${\gamma _{x,y,z}} = \lg \left[ {\frac{{\max \left( {{d_{x - ,y - ,z - }},{d_{x + ,y + ,z + }}} \right)}}{{\min \left( {{d_{x - ,y - ,z - }},{d_{x + ,y + ,z + }}} \right)}}} \right]$ | (4b) |
| ${d_{x - ,y - ,z - }} = \sum\limits_i^{i \in {S_{{\rm{negative}}}}} {} {d_x}_{_i,{y_i},{z_i}}$ | (4c) |
| ${d_{x + ,y + ,z + }} = \sum\limits_j^{i \in {S_{{\rm{negative}}}}} {} {d_x}_{_j,{y_j},{z_j}}$ | (4d) |
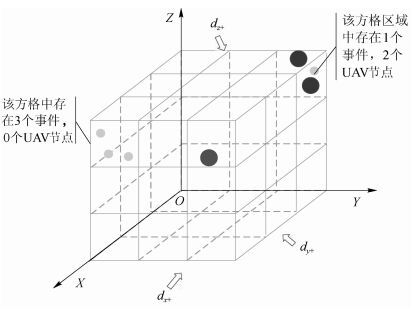
其中:βx, y, z和γx, y, z分别表示移动模型在X、Y、Z 3个维度下的参数,βx, y, z以概率1直接影响节点的移动方向,γx, y, z则通过影响节点移动距离的概率从而间接影响节点的移动距离,两者共同作用于节点移动到新的位置的过程中;log·用于判断两个数的数量级;·表示向下取整;dx+, y+, z+和dx-, y-, z-分别表示节点在X、Y、Z 3个维度下的前后方的方格密度之和,前方为X、Y、Z坐标轴的正方向,后方为X、Y、Z坐标轴的负方向,如图 1所示.
|
图 1 节点访问密度示意图 |
1) 根据式(1) 计算出包括自身在内的,监测区域中27个方格的访问密度dv.
2) 对比包括自身在内的监测区域内的27个方格的访问密度.如果自身所处方格密度最大,则节点不进行任何操作,结束当前运动,在原方格位置上处于悬停状态,进行更细致的搜索.
3) 如果自身所处方格的密度不是最大的,则根据式(4c)和式(4d)计算出节点所处监测范围内节点在X、Y、Z 3个方向上前方密度(正密度d+)和后方密度(负密度d-).
4) 根据式(4a),如果正密度大于等于负密度,即d+≥d-,则设为0,向前进,否则设为1,向后退;根据βx, y, z分别对X、Y、Z 3个维度上对方向进行限定.
5) 根据公式(4b)对改进的高斯参数进行计算,由于文章对公式的界定,所以γx, y, z的值处于区间[0, +∞],如果γx, y, z=0,说明前后密度和的差距没有相差一个数量级,则返回一个参数为(0, 1) 的高斯分布的值;如果γx, y, z≠0,说明前后密度和的差距较大,至少相差一个数量级,进行较大距离移动的概率较大,则返回一个参数为(γx, y, z, 1) 的高斯分布的值,从而增大节点向访问密度较高方向移动较大距离的概率.
3 实验仿真与验证在以UAV机载网络为研究对象的仿真实验中,实验区域设置为长、宽、高分别为100 km的三维空间,每个方格的边长为100 m,节点平均速度为50~100 m/s之间的均匀随机变量.每隔1 s的时间间隔对节点进行一次移动状态的计算和更新.
实验1 移动轨迹曲线的展现.
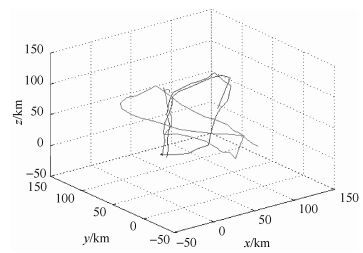
图 2显示的是通过3D-VDGMM移动模型在1 000 s内生成的轨迹图,从图中可以看出通过3D-VDGMM移动模型生成的轨迹平滑,没有急转弯之类的紧急突发状态发生,与实际应用中的状况较符合;该轨迹是通过所处的周围27个方格中探测到的事件数量和存在的UAV数量的密度比即访问密度决定的,所以模型生成的轨迹对于事件敏感,同时避免了聚集现象的发生,使得该移动模型生成的轨迹能够贴近实际需要.
|
图 2 三维移动轨迹 |
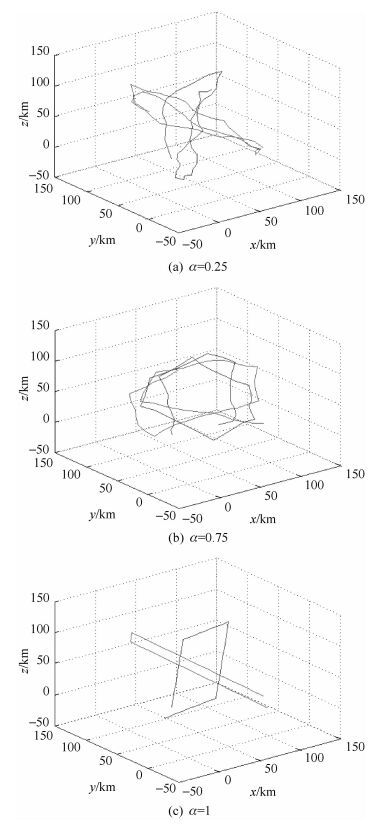
图 3显示的是3D-VDGMM移动模型在不同参数下的轨迹图.从图 3可以发现,随着参数α的逐渐增大,节点移动轨迹的随机性减少而可预测性增加.依据文献[3]中所述,移动模型要求平滑、运动轨迹贴近实际,应用价值才可以体现,图 3中所示为3D-VDGMM移动模型选取不同的参数得到的节点运动轨迹,参数为0.75的时候,运动轨迹平滑,贴近UAV节点的实际运动,所以参数设定为0.75.
|
图 3 不同参数下的三维移动轨迹 |
实验2 节点访问事件的轨迹描绘.
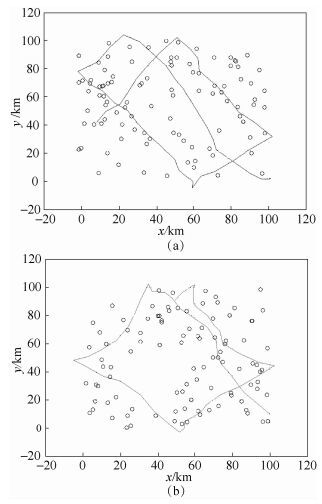
图 4显示的是通过3D-VDGMM移动模型在一段时间内生成的轨迹和在该时间间隔内,事件随机出现在图中的位置.由图 4可见事件出现的位置附近都有轨迹经过,进一步说明了该模型是对事件敏感的,并且在节点行进过程中没有出现急转弯等现象,轨迹平滑,贴近实际需要.
|
图 4 不同节点移动轨迹与随机事件位置 |
实验3 提出模型与3D-GMM在相同时间内,事件搜索数量的对比.
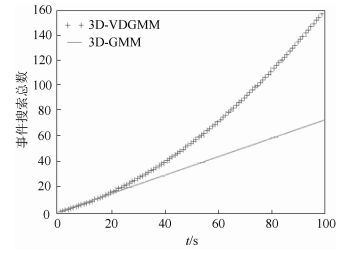
图 5显示的是通过3D-VDGMM移动模型生成的轨迹与一般高斯移动模型生成的轨迹在搜索事件上的比较,横坐标为时间,纵坐标为搜索到事件的总数.可以看出两个模型生成的曲线开始的增长幅度较为接近,随着时间的增长,代表 3D-VDGMM移动模型发现事件总数的心型曲线的增长率逐渐大于代表一般高斯移动模型发现事件总数的实线曲线,这是因为在一般高斯模型中,对于移动模型的搭建没有考虑到事件和UAV对移动模型的影响,对于事件的发现不敏感,因为其下一个位置是随机生成的,仅与上一个节点的位置有关,而事件的生成和消亡也是随机的,所以探索到事件的概率是一样的,故斜率保持不变;而提出模型对于事件是敏感的,所以随着时间的增长,使用该模型的节点是朝着事件多的方向前进,所以探索到事件总数的增长率在增加.
|
图 5 时间-事件总数对比 |
为搭建可靠稳定的UAV机载网络,对现有UAV移动模型进行了优劣分析.在此基础上,改进了3D-GMM模型,提出了一种基于访问密度的新型三维高斯马尔可夫移动模型(3D-VDGMM).首先对调整参数α的实践更新,确保节点的运动轨迹更为平滑真实.随后,通过增加访问密度参数,控制空中节点下一步运动状态的选择,使其更好地捕捉和感知目标事件,实现事件覆盖度的最大化.仿真结果验证了该模型的有效性与合理性,为三维环境下UAV机载网络的性能评估提供了支撑.下一步将基于此模型对UAV机载网络中的通信协议进行详细研究.
| [1] | Erturk M C, Haque J, Arslan H.Challenges of aeronautical data networks[C]//2010 IEEE Aerospace Conference.Montana:IEEE, 2010:1-7. |
| [2] | Bekmezci I, Sahingoz O K, Temel Ş. Flying ad-hoc networks (FANETs):a survey[J]. Ad Hoc Networks, 2013, 11(3): 1254–1270. doi: 10.1016/j.adhoc.2012.12.004 |
| [3] | Broyles D, Jabbar A, Sterbenz J P G. Design and analysis of a 3-D Gauss Markov mobility model for highly-dynamic airborne networks[C]//International Telemetering Conference. Las Vegas:International Foundation for Telemetering, 2009. |
| [4] | Rohrer J P, Centikaya E K, Narra H, et al. AeroRP performance in highly-dynamic airborne networks using 3D Gauss-Markov mobility model[C]//2011 Military Communications Conference. Baltimore:IEEE, 2011:834-841. |
| [5] | Zheng B, Zhang H Y, Huang G C, et al. Design and implemention of a 3-D smooth mobility mode[J]. Journal of Xidian University, 2011, 38(6): 179–184. |
| [6] |
何明, 陈秋丽, 陈希亮, 等. 鱼群启发的三维Ad hoc网络节点随机移动优化模型[J]. 仪器仪表学报, 2014, 35(12): 2826–2834.
He Ming, Chen Qiuli, Chen Xiliang, et al. Fish swarm inspired Ad hoc networks node random mobility optimization model in 3D environment[J]. Chinese Journal of Scientific Instrument, 2014, 35(12): 2826–2834. |


