2. 国网冀北电力有限公司 信息通信分公司, 北京 100053
针对电力数据网对流量异常检测的时效性要求,提出一种改进的局部异常因子异常检测方法KTLAD.该方法基于密度进行检测,计算每个流量包与附近流量包的分隔程度,无需预先设置流量的具体异常状态,相对传统方法具有很高的灵活性.仿真结果验证了KTLAD在电力数据网中业务流量异常检测中的可行性,并且有效地降低了时间成本.
2. Information Communications Branch, State GridJibei North Electric Power Company Limited, Beijing 100053, China
Due to the efficiency requirements of traffic anomaly detection in electric power data network, an improved anomaly detection algorithm named k-d tree based Lof anomaly detection(KTLAD) based on LOF was proposed. Based on density detection, the algorithm calculated the separating level of each traffic package with nearby ones without pre-set specific abnormal state of traffic. Comparing to the traditional algorithms, the proposed algorithm was more flexible. Simulation results showed that the KTLAD was feasible in traffic anomaly detection in electric power data network and reduced time cost effectively.
随着智能电网的建设,电力数据网及其承载的业务系统得到迅猛发展,每天都会有大量的网络流量产生.异常流量混杂在正常流量中,对网络造成极大的损害,会使网络服务质量急剧下降,严重时甚至造成网络瘫痪,这对于可靠性要求极高的电力数据网来说是非常严重的问题.因此,检测异常流量是电力数据网运行维护工作的重要方面.
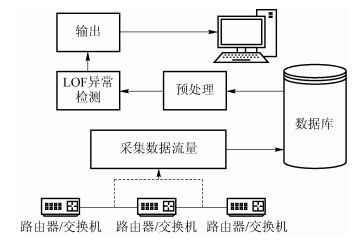
1 异常检测机制基于局部异常因子(LOF, local outlier factor)[1-4]的电力数据网业务流量异常检测流程如图 1所示.
|
图 1 业务流量异常检测流程 |
如图 1所示,首先采集电力数据网流量数据,并对数据执行预处理过程,经过预处理后的数据作为异常检测算法的输入进行异常检测,最后输出检测结果,下面将给出详细论述.
1.1 采集流量数据通过旁路部署在电力数据网网络节点上的流量采集设备采集原始的流量数据包,一般采集到的原始流量数据包共有25个字段,但是原始数据并不适合进行运算,所以还需要进行数据预处理.
1.2 数据预处理由于采集到的原始流量数据比较规律,但某些数据与流量异常检测的关联度不高,因此本文使用数据清理技术对数据进行预处理[5].针对采集到的原始数据,将其导入数据库,从中抽样,提取并归纳每个流量数据包的高关联度字段,最终确定选取PacketsIn、PacketsOut、BytesIn和BytesOut四个字段作为检测数据源.
1.3 基于LOF的异常检测算法局部异常因子(LOF)检测算法是KNN的一个分支,该算法中每个数据都被分配一个局部异常因子,局部异常因子愈大,就认为该数据的异常度越高;反之异常度越小.在常规方法中,算法的第一步中k-距离的计算采用枚举遍历方法,时间成本高,不适用于对可靠性要求和时延敏感度较高的电力数据网,因此本文在计算k-距离时引入了k-d树,提出了一种基于k-d树的LOF异常流量检测算法[6-7].
下一节将详细介绍KTLAD算法.
2 KTLAD算法KTLAD算法的具体步骤如下所述.
2.1 建立k-d树k-d树本质是一个二叉树,每个节点表示一个空间范围,在本文中代表电力数据网的一个数据流量包.k-d树的建立是一个逐级展开分裂的递归过程.一个节点即为一个分裂点(split_point),可分裂为左儿子(left_son)和右儿子(right_son),即分裂点为二叉树的父节点,左儿子和右儿子分别为二叉树的左右子节点,分裂点的分裂方式(split-method)是建立k-d树的关键属性.
k-d树分裂过程的伪代码如下:
1 Begin
2 计算各维度方差;
3 找出方差最大的维度d;
4 各点按在d维度上从小到大排序;
5 中间值点设为split_point;
6 比中间值小的所有点递归上述步骤得到left_son;
7 比中间值大的所有点递归上述步骤得到right_son;
8 End
2.2 计算k-距离与k-距离邻域将一个数据流量包抽象为一个对象p.对任意的自然数k,定义p的k-距离l为p与某个对象o之间的距离,这里的o满足:
至少存在k个对象o′∈D{p}, 使得d (p, o′)≤d (p, o),且至多存在k-1个对象q∈D\{p},使得d (p, q)<d (p, o).
根据已建k-d树,可以容易地查询到最近邻居,而查询第k个最近邻居时可用一个数组来记录一个点是否可以用来更新最近距离,查询得到第k个最近邻居后即可得到k-距离.
接下来,计算对象p的k-距离邻域N.
k-距离邻域的定义如式(1) 所示.
| $N = \left\{ {q|d\left( {p,q} \right) \le l} \right\}$ | (1) |
即p的k-距离邻域包含所有与p的距离不超过l的对象.根据计算k-距离时查询所用数组可以很快得出k-距离邻域.
2.3 计算p相对于o的可达距离给定自然数k,对象p相对于对象o的可达距离r,定义如下:
| $r\left( {p,o} \right) = \max \left\{ {l,d\left( {p,o} \right)} \right\}$ | (2) |
对象p的局部可达密度ρ为对象p与其k-邻域的平均可达距离的倒数,其定义如式(3) 所示.
| $\rho \left( p \right) = \frac{1}{{\frac{{{\sum _{O \in N}}r\left( {p,o} \right)}}{{\left| N \right|}}}}$ | (3) |
最后计算对象p的局部异常因子L (p),对象p的局部异常因子的定义如式(4) 所示.
| $F\left( p \right) = \frac{{{\sum _{o \in N}}\frac{{\rho \left( o \right)}}{{\rho \left( p \right)}}}}{{\left| N \right|}}$ | (4) |
通过异常因子可表示p的异常程度,异常因子接近1的点,表明它和周围点的密度一致,可判定为正常;异常因子越大说明它和周围点的密度相差越大,成为异常点的可能性也就越大.
KTLAD算法的伪代码如下:
1 Begin
2 输入流量数据;
3 Build k-d树; //建立k-d树
4 取一点p;
5 计算p的l; //根据k-d树来计算
6 计算p的N得到a[n]; //根据k-d树来计算,用a数组a[n]来保存
7 Ird_p=0;
8 For (i=0;i<n; i++) //计算对象为Nk-dis中的点
9 { If (l (i)>d (i, p)) //计算可达距离
10 r (i, p)=l (i);
11 Else r (i, p)= d (i, p);
12 ρ(p)+= r (i, p)/n; }
13 ρ(p)=1/ρ(p); //计算局部可达密度
14 F (p)=0;
15 For (i=0;i<n; i++)
16 {计算ρ(i);
17 F (p)+=ρ(i)/n; } //计算异常因子
18 重复上述步骤得出所有点的LOF值;
19 对比阈值得出异常点;
20 End
3 实验与结论 3.1 实验结果通过流量探测工具获取某电力公司数据网2016年3月内的连续流量数据包进行实验.
在实验过程中,k的取值如果过小会存在将异常判为正常的情况,而取值如果过大又会存在将正常判为异常的情况且时间成本会很高,本文折中选取k=30来进行实验.
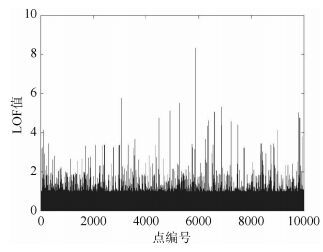
当对1万个连续流量包进行检测时,由于实际数据中有极个别点的异常因子值特别大,放在LOF图中会造成其他数据的异常因子无法区分,如818号点的异常因子值达到84 080,其他LOF值超过10的有24个数据,这24个点必然会判为异常,因此首先去掉这24个异常点后,再显示剩余数据的LOF值分布,如图 2所示.剩余所有数据的LOF值均值仅为1.054,由此可见绝大多数点都分布在1的附近,符合算法的分布状况.
|
图 2 1万个连续流量包检测结果 |
本次实验中异常的阈值取2.5,即所有大于2.5的点判为异常,实际运用中,阈值应该根据实际环境和需求做出相应的调整.
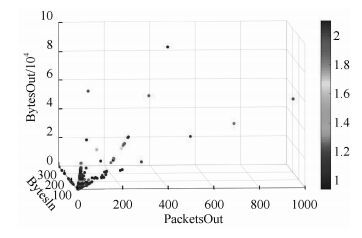
对于整体实验结果来说,本次实验使用的基于密度的算法,密度越大LOF值越接近于1,异常程度越小;密度越小LOF值越大,异常程度越大.图 3为本次实验结果的LOF值密度图,由于人眼只能看得到三维的图形,所以去掉了分析数据中所占比重较小的PacketsIn维度,选取了PacketsOut、BytesIn、BytesOut三个维度作为坐标,以颜色来表示LOF值的大小,图中可以看出越稀疏即密度越小的地区,点的LOF值越大,异常度越高;越密集即密度越大的地区点的LOF值越小,异常度越低.
|
图 3 数据流量包原始分布 |
在计算k-距离时,如果采用枚举遍历的方法,在计算最近邻居时将会遍历所有的对象,计算单个对象的LOF值时时间复杂度将至少为o(n).这里使用k-d树的数据结构来进行优化,由于建立了二叉树,在查询的过程中,虽然具体样本的分布未知,查询过程可能直接从首选子节点中快速查到,也可能需要多次查询各个子树,存在不确定性,但能够将时间复杂度降低到
实验中,分别取k值为5、10、15、20,对相同的样本进行了分析,得出时间对比如表 1所示.可见,使用KTLAD算法在运行时间上具有明显的优势,具体数值分析如表 1所示.
|
|
表 1 不同k取值的时间性能 |
为解决电力数据网业务流量异常检测问题,首先提出了一种基于LOF的流量异常检测机制,并对现有的LOF异常检测算法进行了改进,设计了一种基于k-d树的LOF异常流量检测(KTLAD)算法.根据实验结果可知,笔者提出的KTLAD异常流量检测算法具有无需标签、自适应性强、时效性好等优点,能满足电力数据网业务流量类型的多样化和异常检测的实时性要求.
但是,该方法在第k个最近点查询过程中存在着时间不确定性等不足,因此,后续将对已检测出的异常数据加以区分和处理,增加反馈机制,根据已检测信息对检测过程进行动态修正,提升算法精确判断能力.
| [1] |
穆祥昆, 王劲松, 薛羽丰, 等. 基于活跃熵的网络异常流量检测方法[J]. 通信学报, 2013, 34(z2): 51–57.
Mu Xiangkun, Wang Jinsong, Xue Yufeng, et al. Abnormal network traffic detection approach based on alive entropy[J]. Journal on Communications, 2013, 34(z2): 51–57. |
| [2] | Zhang Ming, Xu Boyi, Gong Jie.An anomaly detection model based on one-class SVM to detect network intrusions[C]//2015 11th International Conference on Mobile Ad-hoc and Sensor Networks (MSN). Shenzhen:[s.n.], 2015: 102-107. |
| [3] |
王宪, 柳絮青, 宋书林, 等. 一种无监督学习的异常行为检测方法[J]. 光电工程, 2014(3): 43–48.
Wang Xian, Liu Xuqing, Song Shulin, et al. Unsupervised learning algorithm for abnormal behavior detection[J]. Opto-Electronic Engineering, 2014(3): 43–48. |
| [4] | Tang X. The stream detection based on local outlier factor[J]. Journal of Information & Computational Science, 2015, 12(17): 6361–6369. |
| [5] |
曲朝阳, 陈帅, 杨帆, 等. 基于云计算技术的电力大数据预处理属性约简方法[J]. 电力系统自动化, 2014, 38(8): 67–71.
Qu Zhaoyang, Chen Shuai, Yang Fan, et al. An attribute reducing method for electric power big data preprocessing based on cloud computing technology[J]. Automation of Electric Power Systems, 2014, 38(8): 67–71. doi: 10.7500/AEPS20130601001 |
| [6] | Tarassenko L, Hayton P, Brady M.Novelty detection for the identification of masses in mammograms[C]//Fourth International Conference on Artificial Neural Networks. London:[s.n.], 1995: 442-447. |
| [7] |
戴健, 丁治明. 基于MapReduce快速kNN Join方法[J]. 计算机学报, 2015, 38(1): 99–108.
Dai Jiang, Ding Zhiming. MapReduce based fast kNN join[J]. Chinese Journal of Computers, 2015, 38(1): 99–108. |


