随着高维信号处理问题的增多，带来了计算复杂度高、信号相关性大、信噪比低等问题.从最早的常规波束形成(CBF, conventional beamforming)方法到多重信号分类(MUSIC, multiple signal classification)，这些算法理论上提高了处理空间信号的角度估计精度、角度分辨力及其他参数精度^[1].然而，对于高维信号处理仍存在分辨力低、计算量大等问题.与传统方法不同，稀疏表示是根据信号的结构特征，将给定的信号在冗余基上进行分解，在变换域上自适应地选择少量的基来准确地表示原始信号，它能有效地提取信号的本质特征，有利于对信号的后续处理，可降低信号处理成本.

为了解决上述问题，提出了基于L₁范数的目标源测向算法.该算法首先对高维信号进行联合稀疏表示，再将角度估计问题抽象成二阶锥归化问题，最后利用凸优化工具箱CVX进行求解.

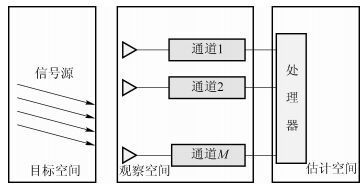
1 阵列信号处理系统 1.1 阵列信号处理模型

假定信号源为窄带信号，考虑N个远场信号入射到空间的某个阵列上.阵列天线由M个传感器(阵元)组成.设通道数与阵元数相同，即阵元接收信号后经各自的传输信道传送到处理器，图 1所示为空间谱估计的系统模型^[1].

理想的情况下，各阵元各向同性，没有互耦、通道不一致等问题^[1].因此，信号在阵元上的增益可以忽略(即g_ki为1)，信号可表示为

$\mathit{\boldsymbol{y}}\left( t \right)=\mathit{\boldsymbol{Ax}}\left( t \right)+\mathit{\boldsymbol{n}}\left( t \right)$

(1)

其中：y (t)表示M×1维阵列快拍数据矢量，n (t)表示M×1维噪声数据矢量，x (t)为空间信号的N×1维矢量，A为空间阵列M×N维流型矩阵，且

$\mathit{\boldsymbol{A}}=\left[ {{\mathit{\boldsymbol{a}}}_{1}}({{\omega }_{0}}){{\mathit{\boldsymbol{a}}}_{2}}({{\omega }_{0}})\ldots {{\mathit{\boldsymbol{a}}}_{N}}({{\omega }_{0}}) \right]$

(2)

信号源之间相干时，表示为^[1]

${{x}_{i}}\left( t \right)={{h}_{i}}{{x}_{0}}\left( t \right),\quad i=1,2,\ldots ,n$

(3)

其中：x₀(t)为基本信源，由它产生阵列上的n个相干信号源；h_i为参数.相干信号源可表示为^[1]

$\mathit{\boldsymbol{y}}\left( t \right)=\mathit{\boldsymbol{Ax}}\left( t \right)+\mathit{\boldsymbol{n}}\left( t \right)=\mathit{\boldsymbol{A}}\left[ \begin{align} & {{h}_{1}} \\ & {{h}_{2}} \\ & \vdots \\ & {{h}_{n}} \\ \end{align} \right]{{x}_{0}}\left( t \right)+\mathit{\boldsymbol{n}}\left( t \right)$

(4)

1.2 稀疏域模型

压缩感知理论是在稀疏信号基础上提出的一种采样与重构的理论^[2].引入全部可能到达角度的过完备正交基$\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}={{\mathbb{R}}^{N\times M}}$来表示A，那么对于简单的无噪声原始信号$\mathit{\boldsymbol{ \boldsymbol{y} }} = {{\mathbb{R}}^{N\times M}}$可用该基矩阵Φ表示：

$\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}}$

(5)

其中：Φ=$\left[ {{a}_{1}}({{{\bar{\omega }}}_{0}}){{\mathrm{a}}_{2}}({{{\bar{\omega }}}_{0}})\ldots {{\mathrm{a}}_{N}}({{{\bar{\omega }}}_{0}}) \right]$，y为被表示信号，x为未知的表示系数，矩阵Φ$\in {{\mathbb{R}}^{N\times M}}$满秩，为欠定方程组的求解问题.

为了得到欠定方程组(5) 的唯一解，可对x加以稀疏性约束，使得逼近原信号y所需要的非零系数较少，信号的表示方法较简化，从而降低信号处理的成本，并且使得方程组有唯一解.基于式(5) 建立的优化表达式为

$\min \left\{ {J\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} x}} = \mathit{\boldsymbol{y}}} \right\}$

(6)

其中y=Φx是约束条件，取目标函数为J (x)=‖x‖₁为目标函数.因为J (x)=‖x‖₁是凸函数，可得到全局的最优解.当x为实数时，L₁范数问题可以简单地转化成线性规划^[3]问题来进行求解；当x为复数时，可采用二阶锥规划求解.

2 基于L₁最小范数的二阶锥规划算法 2.1 基本的二阶锥规划问题

在凸优化中，二阶锥规划形式^[4]为

$\begin{array}{l} \quad \quad \quad \quad \quad \mathop {\min }\limits_x {\mathit{\boldsymbol{f}}^{\rm T}}\mathit{\boldsymbol{x}}\\ {\rm{s}}{\rm{.t}}.{\left\| {{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{b}}_i}} \right\|_2} \le {\mathit{\boldsymbol{c}}_i}^{\rm T}\mathit{\boldsymbol{x}} + {d_i},\quad i = 1,2, \ldots ,N \end{array}$

(7)

其中：x$\in {{\mathbb{R}}^{N\times M}}$为自变量，f$\in {{\mathbb{R}}^{N\times M}}$为常量，A_i∈${{\mathit{\boldsymbol{A}}}_{i}}\in {{\mathbb{R}}^{({{n}_{i}}-1)n}},{{\mathit{\boldsymbol{b}}}_{i}}\in {{\mathbb{R}}^{({{n}_{i}}-1)n}},{{\mathit{\boldsymbol{c}}}_{i}}{{\mathbb{R}}^{n}}$以及${{d}_{i}}\in \mathbb{R}$.式(7) 中的约束为n_i维二阶锥约束^[5].

所要优化的问题在有噪声情况下，可以表示为

$\min {\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}}} \right\|_2} + {\left\| {\lambda \mathit{\boldsymbol{x}}} \right\|_1}$

(8)

其中:λ是正则化参数，它将噪声大小限定在了可允许的范围内.为了利用二阶锥规划算法求解式(8)，将式(8) 用二阶锥规划表示为

$\begin{array}{l} \quad \quad \quad \quad \min \;s + \lambda {1^{\rm T}}t\\ \quad \quad \quad {\rm s.t.}\quad z = \mathit{\boldsymbol{y - Ax}}\\ \quad \quad \quad \quad \quad \quad {\left\| z \right\|_2} \le s\\ {\left\| {{\mathop{\rm Re}\nolimits} ({x_i}),{\mathop{\rm Im}\nolimits} ({x_i})} \right\|_2} \le {t_i},i \in \left\{ {1,2, \ldots ,N} \right\} \end{array}$

(9)

该问题是一个经典的凸优化问题，采用CVX进行求解.最后得到的矩阵x每一行的模值表示空间伪谱，因此得到信号的波达方向估计^[5].

2.2 基于L₁范数的二阶锥规划问题

1) 多帧联合稀疏表示

当获得多帧平稳的快拍数据时，有

$\mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} X}} + \mathit{\boldsymbol{N}}$

(10)

其中：Y=[y (t₁), y (t₂), …, y (t_L)]是天线输出的多帧的数据矩阵，X=[x¹, x², …, x^L]是该多帧信号的稀疏解矩阵，N=[n¹，n²，…, n^L]是噪声.

与单帧信号相比，多帧联合的稀疏处理更加稳健，但是所需要的计算量会随着帧数呈超线性增加，不能满足实时化的波束方向(DOA，direction of arrival)估计需求.

为了解决这个问题，首先对多帧信号进行奇异值分解(SVD)并将观测数据转化到信号子空间上，只对信号子空间进行处理，由于目标源个数远小于快拍数，所以大大提高了计算效率.

对多帧信号模型进行奇异值分解后的结果为

$\mathit{\boldsymbol{Y = \boldsymbol{\varPhi} X + N = ULV}}$

(11)

L₁-SVD所提取的数据表示为

$\begin{array}{l} \quad {\mathit{\boldsymbol{Y}}_{{\rm{SVD}}}} = \mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{V}}^{\rm{H}}}{\mathit{\boldsymbol{D}}_{K\prime }} = \\ \mathit{\boldsymbol{ \boldsymbol{\varPhi} X}}{\mathit{\boldsymbol{V}}^{\rm{H}}}\mathit{\boldsymbol{D}}{\prime _K} + \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{V}}^{\rm{H}}}\mathit{\boldsymbol{D}}{\prime _K} = \\ \quad \quad \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{X}}_{{\rm{SVD}}}} + {\mathit{\boldsymbol{N}}_{{\rm{SVD}}}} \end{array}$

(12)

其中D_K′=[I_K′, 0_{K′×(M-K′)}]^T.降维后保持了原模型的稀疏性及稀疏结构，不影响其对信号方向的估计.

2) 欠定方程组求解

对降维后的数据Y_SVD进行基于L₁范数最优化的稀疏重构问题构造：

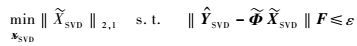
(13)

其中${{{\mathit{\boldsymbol{\tilde X}}}_{{\rm{SVD}}}}}$是X_SVD行稀疏扩展^[5].

基于L₁范数最优化问题利用二阶锥规划表示为

${\left\| {{\mathop{\rm Re}\nolimits} ({{\hat X}_{{\rm{SVD}},i}}),{\mathop{\rm Im}\nolimits} ({{\hat X}_{{\rm{SVD}},i}})} \right\|_2} \le {t_i},i \in \left\{ {1,2, \cdots ,N} \right\}$

(14)

3) 二阶锥规划的算法流程

输入：基矩阵Φ，采样矩阵Y；

输出：X_SVD的逼近值${{{\mathit{\boldsymbol{\tilde X}}}_{{\rm{SVD}}}}}$；

初始化：正则化参数λ=2；

① 对多帧信号Y进行SVD，并将观测数据转化到信号子空间上;

② 定义CVX类型参数s和t;

③ 根据式(14) 在CVX中编写约束条件；

④ 通过CVX凸优化工具包对二阶锥规划问题进行求解，得到满足约束条件的${{{\mathit{\boldsymbol{\tilde X}}}_{{\rm{SVD}}}}}$

3 仿真结果

下面利用10阵元组成的均匀线性阵列对所提算法进行仿真，并与经典的MUSIC算法^[6]、基于L₀范数的OMP算法^[7]和基于L_P范数的最小方差算法^[8]作对比来验证所提出方法的有效性.

实验基于Matlab R2009b、3.19 GHz、1.96 GB RAM PC，主要从算法的均方根误差、分辨力、成功概率以及相干的情况下的估计能力来进行研究.

3.1 均方根误差

DOA估计精度是由均方根误差(RMSE, root mean square error)来衡量的，定义为$\sqrt {\frac{1}{{100}}\sum\limits_{i = 1}^{100} {} ({{\hat \theta }_i} - \theta )2} $其中${{{\hat \theta }_i}}$为第i次实验的估计角度.

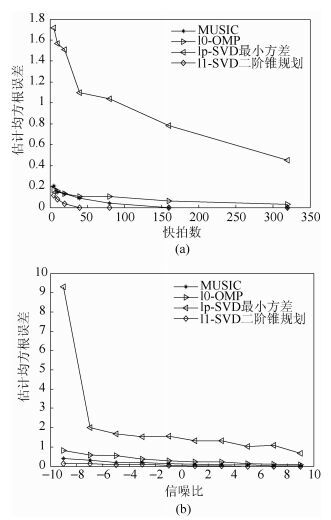
如图 2(a)所示，考虑信噪比为10 dB，均方根误差随着快拍数的增加而减小，其中迭代加权最小方差法在低快拍数的情况下估计误差较大，二阶锥规划估计误差最小.由图 2(b)可知，设定快拍数200，信噪比从-10 dB到10 dB变化.估计均方根误差随着信噪比的增加而减小，其中二阶锥规划方法在低信噪比的时候误差也较小.

3.2 可分辨次数

对可分辨进行定义：在某次实验中，若$\left| {{{\hat \theta }_1} - {\theta _1}} \right|$和$\left| {{{\hat \theta }_2} - {\theta _2}} \right|$都小于|θ₁-θ₂|/2 (其中${{{\hat \theta }_k}}$和θ_k分别表示第k个信号DOA的估计值与真实值)，则认为本次实验中的2个信号是可分辨的^[5]；否则，这2个信号不可分辨.

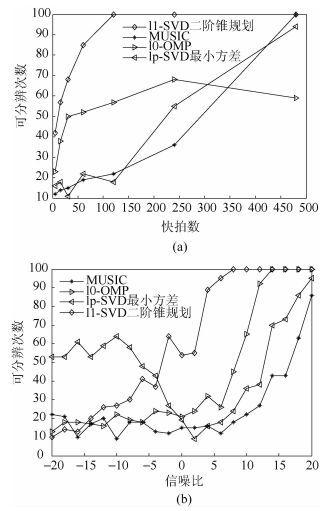
如图 3(a)所示，信噪比为10 dB，目标方向为-10°和10°，快拍数从5~300变化，可分辨次数随着快拍数的增加而增加，在快拍数较高的情况下呈现较好的分辨力，其中基于二阶锥规划在低快拍数时也能得到较高的分辨力.如图 3(b)所示，信噪比从-20°~20°变化，可分辨次数大体趋势随着信噪比的增加而增加.在信噪比低于0 dB时，由于噪声的影响较大，可分辨次数出现高低起伏状态.其中二阶锥规划算法在较低信噪比情况下也有较好的可分辨性能.

3.3 成功概率

对成功概率定义为式(16)，当$\max \left( {\left| {{{\hat \theta }_{i,k}} - {\theta _k}} \right|} \right) ＜ 1$(这里，${{{\hat \theta }_{i,k}}}$表示第i次实验的第k个信号的估计角度)时认为第i次实验估计成功，否则估计失败.

${\rm{PER = }}\frac{成功估计信号次数}{仿真总次数}$

(16)

如图 4(a)所示，信噪比为10 dB，目标方向为-10°和10°，快拍数从5~300变化.成功概率随着快拍数的增加而增加，其中二阶锥规划的算法和MUSIC算法在整个快拍数范围内的估计成功概率都接近100%.如图 4(b)所示，信噪比从-10°~10°变化.成功概率随着信噪比的增加而增加，其中二阶锥规划的算法在低信噪比的时候估计成功的概率都接近100%.

3.4 相干信号

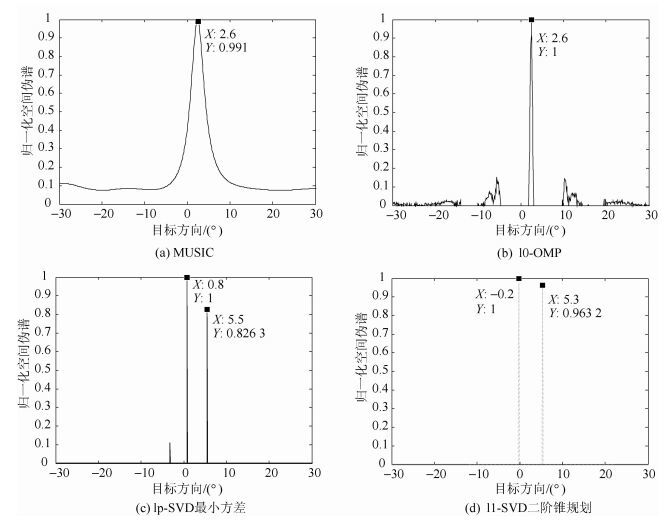
最后考虑相干信号的处理情况，相干与不相干在信号上体现，只要2个信号的频率不一样，这2个信号就是不相干的. 2个目标方向为0°和5°时，如图 5迭代加权最小方差法和二阶锥规划方法能够得到大致准确的估计结果，而MUSIC算法和OMP算法估计明显不能分辨.

4 结束语

立足于窄带信号阵列输出的稀疏表示，对稀疏重构算法进行研究，提出了基于L₁范数的二阶锥归化算法.该算法首先对高维信号进行奇异值分解来降低计算的复杂度，再利用CVX进行二阶锥规划求解.随后将该算法与传统的MUSIC算法及其他两种最小范数法的典型算法进行比较，验证了该算法的有效性.仿真结果表明，二阶锥规划算法在较大的信噪比范围内都能取得较低的重构误差和较高的成功概率，对相关性较大的信号也能进行识别，能够求解多个信号源的情况.