2. 国网北京市电力公司 信息通信分公司, 北京 100761
针对电力通信网中以顺序配置为主的业务路由配置策略可能导致网络风险不均衡的问题,综合考虑现网的各项参数要求以及业务分布因素,提出了一种基于多蚁群算法的路由配置机制.首先对关键业务路由配置问题建模,定义了通道压力,并构建了通道压力最小化的数学模型.之后结合模型特征利用多蚁群算法进行求解,最后基于现网拓扑结构进行仿真实验.实验结果表明,在不同规模的网络中,相对于其他方法,该机制能获取全局通道压力值更低的业务路由配置方案.
2. State Grid Information and Telecommunication Branch, Beijing 100761, China
At present, it is possible for service routing method based on sequential configuration to cause the high risk of power communication network. To solve the key service routing problem, a routing allocation strategy based on multiple ant colony algorithms was proposed, considering all parameter requirements of current network and business distribution factors. Firstly, the routing allocation model of electric power communication network service was built up. By defining the channel pressure, the model with minimum channel pressure was designed. Then multiple ant colony algorithms were used to solve the problem. Finally, the simulation experiment based on the current network topology was carried out. Simulation results showed that the proposed method could provide efficient network planning solution in different scale networks with higher performance than other methods.
电力通信网是电力系统中重要的组成部分,保证了电网的稳定运行.电力通信业务与电力系统生产、调度和控制密切相关,同时电力通信安全风险有着严格的等级划分,规定了每个风险等级对应的业务种类、数量及受影响程度[1],减少高级别的电力通信安全风险是电力通信部门的重要目标.
在智能优化算法方面,陆等[2]中提出了多蚁群算法的网络负载动态均衡方法,使用多种群的思路进行问题求解,扩展了蚁群算法应用场景. Liu等[3]利用启发式算法求出两点之间的前k条最短路径,通过将可用带宽最大的路径作为业务路由的方式实现负载均衡. Chang等[4-5]分别采用不同的启发式算法实现基于负载均衡的业务路由配置,并以带宽利用率作为约束条件.然而,这些算法仅以带宽的业务均衡分布,算法未考虑业务重要度因素,致使其不适用于解决电力通信网中基于业务重要度的业务风险分布问题.同时大部分路由配置策略为顺序配置业务,不能处理多个业务同时配置路由的问题.
考虑全局风险的多个业务同时部署问题,提出一种基于多蚁群算法的关键业务路由配置算法.算法在考虑通道压力的基础上,对业务进行部署.经过接近现网的拓扑仿真,验证算法的可靠性及优化能力;且相比于其他路由算法,在多业务场景中能有效优化业务路径的通道压力值,使网络通道压力总值最低,降低风险.首先建立网络拓扑模型并定义通道压力值,在此基础之上分析关键业务路由配置问题并提出基于多蚁群算法的业务路由配置机制.之后对该机制进行仿真实验,验证其收敛性和优化能力.
1 关键业务路由配置建模 1.1 网络拓扑模型为了抽象电力通信网中关键业务的路由配置问题,首先定义网络拓扑图G (V, E),其中V={v1, v2, …, vn}代表节点的集合,E={e12, e13, …, e(n-1) n}代表节点间链路的集合,其下标代表链路两端的节点编号;同时有业务集合S={s1, s2, …, sn}.其中业务sn具有重要度参数dn,是根据业务分类设定的权值.对于网络中的任意节点组合,有p (i, j)={vi, vk, …, vj},其起点和终点分别为vi和vj.如果满足∀vm, vn∈p (i, j),vm≠vn,即路径上不存在环,同时路径上所有相邻两节点之间均至少存在一条边,则称p (i, j)为节点vi和vj之间的一条路径,节点vi和vj之间的路径构成的集合为P (i, j).在已确定所有业务的业务路径的情况下,可以获得与业务一一对应的业务路径:pn(vnstart, vnend)∈P (vnstart, vnend),其中下标n代表所对应的业务,下标start以及end分别代表该节点是业务的起始与终止节点.对于任意两节点vi和vj间的链路eij,即可通过业务路径得知其上承载了哪些业务.同时业务路径有时延Tn,且有时延门限Tthresholds.
| ${{T}_{n}}=\frac{{{L}_{n}}\gamma }{c}+\sum\limits_{v\in {{p}_{n}}}{{}}t\left( v \right)$ | (1) |
其中:Tn为业务路径pn的时延,Ln为路径光纤总长度,γ为光纤芯区折射率,c为真空中的光速,t (v)为节点时延.
1.2 通道压力这里定义通道压力值,对于链路上承载的不同业务,根据业务的种类可以赋予不同的量化重要度,例如线路保护业务和安全稳定控制业务这两种最为重要的业务,即赋予最高的重要度;之后计算链路上所有业务重要度之和就可以得到一个表示链路上业务负载大小的量化指标,即为通道压力值Pr(eij).通道压力值是链路承载的所有业务的重要度总和,利用它可以有效区分高压与低压链路,通道压力的表达式为
| $\Pr ({{e}_{ij}})=\delta \sum\limits_{{{s}_{n}}\in S}{{}}{{d}_{n}}({{e}_{ij}}\in {{p}_{n}}(v_{n}^{\text{start}},v_{n}^{\text{end}}))$ | (2) |
其中δ为通道压力权值,根据重要度之和进行分级,达到区分不同级别通道压力的作用.
1.3 问题分析算法的优化对象为全部业务路由
| $P=\{{{p}_{n}}(v_{n}^{\text{start}},v_{n}^{\text{end}}),{{s}_{n}}\in S\}$ | (3) |
优化目标为业务部署后的全局通道压力值,约束条件为任意业务路径的路径时延均小于等于时延门限值,构建优化模型如下:
| $\underset{P}{\mathop{\min }}\,\sum\limits_{{{e}_{ij}}\in E}{{}}\Pr ({{e}_{ij}})\quad \text{s}\text{.t}.\quad \forall {{p}_{n}}\in P,{{T}_{n}}\le {{T}_{\text{thresholds}}}$ | (4) |
单只蚂蚁是蚁群算法的核心,可以视它为在拓扑图G上不断移动的探测指针,同时它可以存储移动过程中经过的节点与路径.定义蚂蚁ank,以及蚁群An,与业务集合S中的业务一一对应,这里An={an1, an2, …, ank}.对于蚂蚁ank中,上标k代表蚂蚁在蚁群中的序列,下标n代表蚂蚁对应的业务. An中,n代表蚁群所对应的业务.对于单一蚂蚁,它具有对应业务的起始节点vnstart与终止节点vnend信息.
2.1 概率转移算子在算法执行过程中,蚂蚁需要对相邻链路的信息素浓度进行判断,利用转移概率公式决定移动方向.蚂蚁转移概率公式如下:
| $F_{ij}^{k}\left( t \right)=\left\{ \begin{array}{*{35}{l}} \frac{{{\tau }_{ij}}(t,{{A}_{n}}){{\eta }_{ij}}}{\sum\limits_{{{v}_{s}}\in V_{\text{allowed}}^{i}}{{}}{{\tau }_{is}}(t,{{A}_{n}}){{\eta }_{is}}},{{v}_{j}},{{v}_{s}}\in V_{\text{allowed}}^{i} \\ 0,\quad 其他 \\ \end{array} \right.$ | (5) |
其中:Fijk(t)为循环代数t时蚂蚁k从vi节点到vj节点的转移概率,vj与vs属于所有vi节点可连通节点集合Vallowedi,即对任意属于Vallowedi的节点vj,均存链路eij使vi和vj相连;τij(t, An)为链路eij在循环代数t时的蚁群An的信息素浓度,ηij为链路eij的期望值,本算法中设计为通道压力的倒数.
2.2 信息素浓度初值在普通的蚁群算法中,由于初始信息不足,算法运行初期的收敛速度慢,蚂蚁寻路的效率低下.为了提高算法运行初期的收敛效果,将通道压力值归一化之后转化为符合信息素浓度取值范围的参数,并依照该参数部署信息素浓度初始值,即
| ${{\tau }_{ij}}^{\alpha }(0,{{A}_{s}})={{\tau }_{\min }}+({{\tau }_{\max }}-{{\tau }_{\max }})\frac{\Pr ({{e}_{ij}})}{{{\Pr }_{\max }}}$ | (6) |
其中Prmax代表网路全部链路中通道压力值的最大值.
2.3 信息素浓度更新当全部种群的所有蚂蚁执行过一次算法,则认为一个循环完成并更新信息素,同时初始化种群继续下一个循环.信息素更新方法如下:
| ${{\tau }_{ij}}(t+1,{{A}_{n}})=\rho {{\tau }_{ij}}(t,{{A}_{n}})+\Delta {{\tau }_{ij}}(t,{{A}_{n}})$ | (7) |
其中:τij(t+1, An)为节点更新后的蚁群An信息素浓度,ρ为衰减因子,τij(t, An)为节点在t循环时的信息素浓度,Δτij(t, An)为有效路径上的信息素增加值,且有
| $\Delta {{\tau }_{ij}}(t,{{A}_{n}})=\sum \Delta {{\tau }_{ij}}^{k}(t,{{A}_{n}})$ | (8) |
信息素增加值为种群k只蚂蚁平均信息素浓度Δτijk(t, An)的总和,又有
| $\Delta {{\tau }_{ij}}^{k}(t,{{A}_{n}})=\left\{ \begin{array}{*{35}{l}} \frac{Q}{\sum\limits_{{{e}_{ij}}\in p}{{}}\Pr ({{e}_{ij}})},{{T}_{k}}\le {{T}_{\text{thresholds}}} \\ 0,{{T}_{k}}\ge {{T}_{\text{thresholds}}} \\ \end{array} \right.$ | (9) |
| ${{T}_{k}}=\frac{{{L}_{k}}\gamma }{c}+\sum\limits_{v\in {{p}_{ij}}}{{}}t\left( v \right)$ | (10) |
平均信息素浓度Δτijk(t, An)为蚂蚁携带信息素量Q除以该蚂蚁当前路径的通道压力总值,其中上标k代表该蚂蚁在种群中的序列号.蚂蚁携带信息素量Q为设定定值,它决定了一次有效寻路之后全局信息素浓度增加量的总值.
在算法执行过程中,当蚂蚁移动路径的时延总和超过关键业务要求的给定门限时,需要强制终止该蚂蚁的移动,并且直接使下一个蚂蚁进入网络拓扑执行算法.被强制终止的蚂蚁不会更新信息素,保证无效数据不会污染信息素分布.其中Tk为蚂蚁k移动经过的链路与节点的总时延,Lk为移动总距离.
2.4 多种群信息素交互为了能够有效疏散路径,减小通道压力,针对同一节点上多个蚁群的信息素分布进行设计.首先,不同种群的信息素浓度在概率转移计算中不相互影响,蚂蚁仅通过自己种群的信息素浓度来判断行进方向.其次,为了实现通道压力的优化以及多业务的同步路由配置,设定不同种群共享的信息素浓度上下限,即
| ${{\tau }_{\min }}\le \sum\limits_{{{s}_{n}}\in S}{{}}{{\tau }_{ij}}(t,{{A}_{n}})\le {{\tau }_{\max }}$ | (11) |
同时,对于同一节点上不同蚁群,其信息素共享上下限,当某次更新后信息素超过上下限时,则按比例调整节点信息素总值为上下限,即
| $\left. \begin{align} & {{\tau }_{ij}}(t,{{A}_{s}})=\frac{{{\tau }_{\max }}}{\sum\limits_{{{s}_{n}}\in S}{{}}{{\tau }_{ij}}(t,{{A}_{n}})}{{\tau }_{ij}}(t,{{A}_{n}}),\sum\limits_{{{s}_{n}}\in S}{{}}{{\tau }_{ij}}(t,{{A}_{n}})\ge {{\tau }_{\max }} \\ & {{\tau }_{ij}}(t,{{A}_{s}})=\frac{{{\tau }_{\min }}}{\sum\limits_{{{s}_{n}}\in S}{{}}{{\tau }_{ij}}(t,{{A}_{n}})}{{\tau }_{ij}}(t,{{A}_{n}}),\sum\limits_{{{s}_{n}}\in S}{{}}{{\tau }_{ij}}(t,{{A}_{n}})\le {{\tau }_{\min }} \\ \end{align} \right\}$ | (12) |
为了验证提出机制的有效性以及相对于其他优化算法的表现,在接近现网的拓扑下进行仿真.在实验仿真中,参考文献[6],设置节点信息素浓度上下限分别为60和10,单只蚂蚁信息素携带量Q为1 000,衰减因子设为0.7.每个蚁群中有30只蚂蚁,循环代数为30代.实验依次设定网络节点数量10,20,50,仿照现网实际情况设定节点联通情况,即节点间联通比例为30%.
3.2 结果分析1) 收敛过程分析
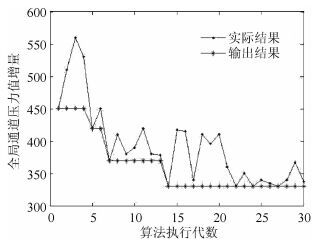
对每一代的路径结果进行记录并计算通道压力值,得出如图 1所示的算法收敛过程.可以看到在25代左右算法收敛.
|
图 1 算法收敛过程 |
2) 算法优化性能分析
对比Dijkstra算法和遗传算法与多蚁群算法的性能表现.其中遗传算法设计循环代数100代,种群数量为每个业务对应100组基因,编码方式为实数编码,交叉概率为60%,变异概率为0.5%.多个业务的基因形成基因组执行算法,实现同时配置多个业务的业务路径. Dijkstra算法为顺序配置路径,以通道压力为网络拓扑权值选择通道压力总值最小的路径为当前业务的业务路径.
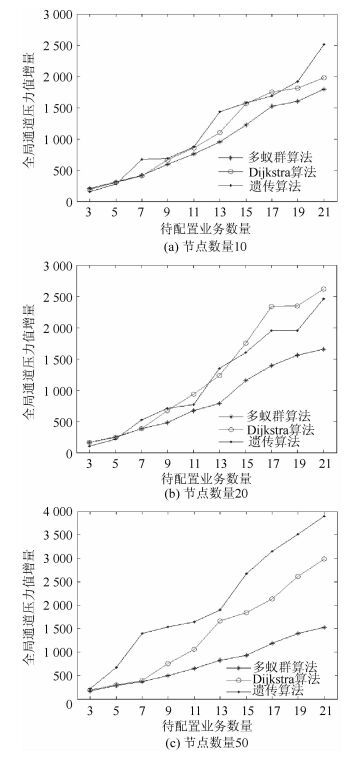
从图 2可知,在待配置业务数量低时,3种算法优化性能相近.但是当待配置业务数量以及网络节点逐渐增加,Dijkstra算法以及遗传算法的优化效果迅速劣化,表现远差于多蚁群算法,说明提出算法相对Dijkstra算法以及遗传算法在多节点多业务的环境中有着更好的优化性能.
|
图 2 算法性能对比 |
为了解决电力通信网多业务部署时通道压力不均衡导致线路高压的问题,提出了一种基于多蚁群的电力通信网的路由配置机制.首先,综合设备和线路的通道压力、业务特征,设置蚁群以及信息素;之后,提出了一种基于种群信息素交互的多蚁群改进法来确定业务的路径.经过接近现网的拓扑仿真,验证了该机制相对于其他方法,能有效优化网络的通道压力指标.实验结果表明,所提算法能够很好地处理对多业务同时配置路由的问题.下一步将基于实际电力通信网网络拓扑改进优化算法,提升应用价值与说服力.
| [1] | 中国南方电网有限责任公司. Q/CSG11104002-2012, 南方电网运行安全风险量化评估技术规范[S]. 北京: 中国电力出版社, 2012: 3-5. |
| [2] |
陆俊, 祁兵. 多蚁群算法的网络负载动态均衡方法[J]. 计算机应用, 2008, 28(3): 572–575.
Lu Jun, Qi Bing. Multiple ant colony algorithm load balancing for network sessions[J]. Journal of Computer Applications, 2008, 28(3): 572–575. |
| [3] | Liu Nianzu, Chen Xiao. Overlay multicasting at a path-level granularity for multi homed service nodes[C]//International Conference on Information Science and Technology (ICIST 2011). Nanjing: IEEE, 2011: 939-946. |
| [4] | Chang H Y. A multipath routing algorithm for degraded-bandwidth services under availability constraint in WDM networks[C]//26th International Conference on Advanced Information Networking and Applications Workshops (WAINA 2012). Fukuoka: IEEE, 2012: 881-884. |
| [5] | Santos J, Pedro J, Monteiro P, et al. Impact of collocated regeneration and differential delay compensation in optical transport networks[C]//IEEE Eurocon-international Conference on Computer as a Tool (EUROCON 2011). Lisbon: IEEE, 2011: 1-4. |
| [6] |
吴华锋, 陈信强, 毛奇凰, 等. 基于自然选择策略的蚁群算法求解TSP问题[J]. 通信学报, 2013, 34(4): 165–170.
Wu Huafeng, Chen Xingqiang, Mao Qihuang, et al. Improved ant colony algorithm based on natural selection strategy for solving TSP problem[J]. Journal on Communications, 2013, 34(4): 165–170. |


