2. 国家计算机网络应急技术处理协调中心, 北京 100029
针对互联网计算资源数量大、类型多、随机性强、稳定性相对较差等特点,提出一种基于朴素贝叶斯分类的iVCE云平台资源可靠性评价算法.通过对计算资源的特征提取,离散化处理后,使用概率估计方法对资源的状态做出实时的评价.在iVCE平台的实际运行效果表明,平台资源可靠性评价通过引入朴素贝叶斯算法,在评价的准确性方面提升了20%以上,通过参数优化算法的准确率同样好于同类其他同类算法2%以上,满足了实际生产的需求.
2. National Computer Network Emergency Response Technical Team/Coordination Center, Beijing 100029, China
The computing resources of the Internet has a large number, type, strong randomness, more stability are relatively poor, a kind of based on naive bayesian classification virtual computing environment(iVCE)[1-2] cloud platform reliability evaluation algorithm is put forward. After the feature extraction of computing resources, the method of probability estimation is used to estimate the state of the resources in real time. Had indicated in the actual operation of the iVCE platform, platform resource reliability evaluation by using naive Bayesian algorithm, in evaluation of the accuracy of a 20% increase over and through the parameter optimization algorithm accuracy was also better than similar to several other algorithms above 2%. Meet the needs of the actual production.
iVCE平台的设备主要由互联网上的资源组成,这些计算资源具有数量大、类型多、随机性强、稳定性相对较差等特点.如何适应互联网资源不稳定问题,让这些海量的资源发挥其庞大的计算能力具有非常重要的意义.笔者提出一种基于朴素贝叶斯分类的iVCE云平台资源可靠性评价算法.算法通过对计算资源的特征提取,离散化处理,使用概率估计方法对资源的可靠性做出实时的评价.通过在iVCE平台的实际运行效果表明,算法有效地提高了平台任务的执行成功率和工作效率,满足了实际生产的需求.
1 朴素贝叶斯算法朴素贝叶斯(naive Bayes)算法是基于贝叶斯公式与特征条件独立假设的分类方法,设输入空间χ⊆Rn为n维向量的集合,输出空间为类标记集合γ={c1, c2, …, ck}.输入为特征向量x∈χ,输出为类标记(class label)y∈γ. X是定义在输入空间χ上的随机变量,Y是定义在输出空间γ上的随机变量. P(X, Y)是X和Y的联合概率分布.训练数据集T={(x1, y1), (x2, y2), …, (xn, yn)},由于P(X, Y)是独立同分布产生.朴素贝叶斯法通过训练集掌握学习联合概率分布P(X, Y)后,来估计新实例的后验概率.
先验概率分布:
| $ P\left( {Y = {c_k}} \right), \;\;k = 1, 2, \cdots, K $ | (1) |
条件概率分布:
| $ \begin{array}{l} P\left( {X = x|Y = {c_k}} \right) = \\ P\left( {{X^{(1)}} = {x^{(1)}}, \ldots, {X^{(n)}} = {x^{(n)}}|Y = {c_k}} \right), \\ k = 1, 2, \cdots, K \end{array} $ | (2) |
于是学习到联合概率分布P(X, Y).设x(j)可能取值有S(j)个,j=1, 2, …, n,Y可取值有K个,那么参数为
朴素贝叶斯法对条件概率分布作了条件独立性的假设.故条件概率分布可表示为
| $ \begin{array}{l} \left( {pX = x|y = {c_k}} \right) = \\ p\left( {{X^{(1)}} = {x^{(1)}}, \cdots, {x^{(n)}} = {x^{(n)}}|y = {c_k}} \right) = \\ \mathop \prod \limits_{j = 1}^n p({X^{(j)}} = {x^{(j)}}|y = {c_k}) \end{array} $ | (3) |
朴素贝叶斯法实际上学习到生成数据的机制,所以属于生成模型.算法通过使用条件独立假设使朴素贝叶斯法变得简单、高效.
朴素贝叶斯法分类时,对给定的输入x, 通过学习到的模型计算后验概率分布P(Y=ck|X=x),将后验概率最大的类ck作为x的类输出.后验概率计算根据贝叶斯公式进行:
| $ \begin{array}{l} P(Y = {c_k}|X = x) = \\ \frac{{P(Y = {c_k}){\prod _j}P({X^{(j)}} = {x^{(j)}}|Y = {c_k})}}{{{\sum _k}P(Y = {c_k}){\prod _j}P({X^{(j)}} = {x^{(j)}}|Y = {c_k})}}, \\ k = 1, 2, \cdots, K \end{array} $ | (4) |
朴素贝叶斯分类器可以表示为
| $ \begin{array}{l} y = f\left( x \right) = \\ \mathop {{\rm{argmax}}}\limits_{\;\;\;\;{c_k}} \frac{{P(Y = {c_k}){\prod _j}P({X^{(j)}} = {x^{(j)}}Y = {c_k})}}{{{\sum _k}P(Y = {c_k}){\prod _j}P({X^{(j)}} = {x^{(j)}}Y = {c_k})}} \end{array} $ | (5) |
iVCE是基于互联网的云计算平台,平台核心部分分为应用层、任务管理层、资源管理层和虚拟资源层.每个资源可以由一系列特征表示为
X={ Cpu_usage, Mem_usage, Disk_usage, Net_type, Net_usage, Net_status, Process_number, Online_time, IPaddr, Cur_time, Task_type…}
虚拟资源xi=(xi(1), xi(2), …, xi(m))T, xi(j)是第i个虚拟资源的第j个特征,xi(j)∈{aj1, aj2, …, ajSj}, ajl是第j个特征可能取的第l个值,如high| medium |low,j=1, 2, …, n, l=1, 2, …, Sj, yi∈{c1, c2, …, ck}.
资源管理层主要包括虚拟资源的各种状态收集、资源评价(可靠性、实时性等)和向任务管理层推荐资源等功能.资源管理层也是本算法的应用层,其解决的问题是:当收到任务任务管理层的对特定类型的应用进行资源请求时,资源调试算法如何对已知资源的可靠性进行评价,然后将最合适的资源推荐给任务管理服务器.问题可描述为如何通过对历史资源的特征值和任务的执行结果进行学习,得到任务执行成功率的先验概率和相应的任务执行结果与资源特征值的条件概率,最后根据当前等待分配的资源的特征值,计算这些资源执行相应类型任务的后验概率,然后将一组任务成功率最高的资源推荐给任务管理服务器,故可用式(5) 进行描述,其中P(Y=ck)表示平台任务执行总的成功率和失败率,ck={success, failure}. P(X(j)=x(j)|Y=ck)表示相应任务的执行结果对应的资源特征的后验概率,x(j)表示第j个特征,目标求资源x属于类别y的概率.
2.2 算法步骤算法输入:训练数据集,iVCE平台历史各个资源属性值和与其对应任务执行结果.
算法输出:实例x的概率分类.
算法步骤如下.
1) 数据清洗, 包括3个方面:数据获取与特征提取;对缺失数据进行补充,处理负值特征值;将数据型属性离散化.
2) 计算样本数据中任务执行的成功率和失败率.
| $ p(Y = {c_k})\frac{{\mathop \sum \limits_{i = 1}^N I({y_i} = {c_k})}}{N}, k = 1, 2, \cdots, K $ |
3) 计算样本数据中各个特征值在特定任务执行结果的条件概率.
| $\begin{array}{l} p({X^{(j)}} = {a_{jl}}|Y = {c_k}) = \frac{{\mathop \sum \limits_{i = 1}^N I(x_{_i}^{^{(j)}} = {a_{jl, }}{y_i} = {c_k})}}{{\mathop \sum \limits_{i = 1}^N I({y_i} = {c_k})}}\\ j = 1, 2, \cdots, n;l = 1, 2, \cdots, {S_j};k = 1, 2, \cdots, K \end{array} $ |
4) 计算给定实例x=(x(1), x(2), …, x(n))T预测其执行任务的成功率方法.
| $ P(Y = {c_k})\mathop \prod \limits_{j = 1}^n P({X^{(j)}} = {x^{(j)}}Y = {c_k}), k = 1, 2, \cdots, K $ |
5) 选择概率最高的分类ck,记录分类的概率值.
| $ y = {\rm{arg}}\mathop {{\rm{max}}}\limits_{{c_k}} P(Y = {c_k})\mathop \prod \limits_{j = 1}^n P({X^{(j)}} = {x^{(j)}}Y = {c_k}) $ |
上述算法应用到实际的生产环境中.任务的执行结果可分为成功和失败,目标是使用朴素贝叶斯算法通过资源的历史特征和任务的历史执行结果进行训练,然后根据当前资源的特征对其任务执行的成功率进行预测.其中训练的样本集T=100万个,资源的属性包括资源ID、CPU利用率、内存利用率、硬盘利用率、网络类型、网络利用率、网络状态、进程数量、平均在线时长、IP地址、当前时间、任务类型等,算法在参数、数据选择上参考文献[3-4],对虚拟机的特征向量进行提取.任务的执行结果包括成功或者失败.测试实例x为
| $ \left\{ \begin{array}{l} {\rm{cpu\_usage = low, mem\_usage = medium, }}\\ {\rm{disk\_usage = high, net\_type = fixed, }}\\ {\rm{net\_usage = high}} \cdots \end{array} \right\} $ |
训练数据集为T={(x1, y1), (x2, y2), …(xn, yn)},特征集为
| $ X{\rm{ = }}\left\{ \begin{array}{l} {\rm{Cpu\_usage, Mem\_usage, Disk\_usage, }}\\ {\rm{Net\_type, Net\_usage, Net\_status, }}\\ {\rm{Process\_number, Online\_time, }}\\ {\rm{IPaddr, Cur\_time, Task\_type }}\cdots \end{array} \right\} $ |
假设空间Y={success, failure},通过步骤2) 计算得到
| $ \begin{array}{l} P\left( {{\rm{Result = success}}} \right) = 0.998\\ P\left( {{\rm{Result = failure}}} \right) = 0.002 \end{array} $ |
各特征x(j)的取值为
| $ \begin{array}{l} {S_{{\rm{(cpu\_usge)}}}}{\rm{ = }}\left\{ {{\rm{high, medium, low}}} \right\}\\ {S_{{\rm{(mem\_usge)}}}}{\rm{ = }}\left\{ {{\rm{high, medium, low}}} \right\}\\ {S_{{\rm{(disk\_usge)}}}}{\rm{ = }}\left\{ {{\rm{high, medium, low}}} \right\}\\ {S_{{\rm{(net\_type)}}}}{\rm{ = }}\left\{ {{\rm{fixed, mobile}}} \right\}\\ {S_{{\rm{(net\_usage)}}}}{\rm{ = }}\left\{ {{\rm{high, medium, low}}} \right\}\\ {S_{{\rm{(net\_status)}}}}{\rm{ = }}\left\{ {{\rm{high, medium, low}}} \right\}\\ {S_{{\rm{(process\_number)}}}}{\rm{ = }}\left\{ {{\rm{high, medium, low}}} \right\}\\ {S_{{\rm{(task\_type)}}}}{\rm{ = }}\left\{ {{\rm{calculate, store, bandwidth, lowdelay}}} \right\} \end{array} $ |
通过步骤3) 计算各个特征值的条件概率为
| $ \begin{array}{l} P\left( {{\rm{cpu\_usage = low|success}}} \right) = 0.68\\ P\left( {{\rm{cpu\_usage = low|failure}}} \right) = 0.31\\ P\left( {{\rm{mem\_usage = medium|success}}} \right) = 0.56\\ P\left( {{\rm{mem\_usage = medium|failure}}} \right) = 0.48 \end{array} $ |
其他特征值的计算方法同上,联合概率计算方法为
| $ \begin{array}{l} P\left( {{\rm{success}}} \right)P\left( {{\rm{cpu\_usage = low|success}}} \right)\\ P\left( {{\rm{mem\_usage = medium|success}}} \right)\\ P\left( {{\rm{net\_usage = high|success}}} \right)\\ P\left( {{\rm{disk\_usage = high|success}}} \right) \cdots = \\ 0.998 \times 0.68 \times 0.56 \times \cdots = 0.078\\ P\left( {{\rm{failure}}} \right)P\left( {{\rm{cpu\_usage = low|failure}}} \right)\\ P\left( {{\rm{mem\_usage = medium|failure}}} \right)\\ P\left( {{\rm{net\_usage = high|failure}}} \right)\\ P\left( {{\rm{disk\_usage = high|failure}}} \right) \cdots = \\ 0.002 \times 0.31 \times 0.48 \times \cdots = 0.023 \end{array} $ |
归一化处理得到此资源执行本次任务的成功率为77%,失败率为22.7%.
| $ \begin{array}{l} P\left( {{\rm{success}}} \right) = 0.078/0.078 + 0.023 = 77\% \\ P\left( {{\rm{failure}}} \right) = 0.023/0.078 + 0.023 = 22.7\% \end{array} $ |
kNN(k-NearestNeighbor)、决策树(Decision Tree)、Logistic回归等算法明确给出结果相比,朴素贝叶斯算法不但能给出结果属于哪一类,而且还能给出属于哪一类的概率.这些概率更适合平台资源随机性强的特点.算法易于理解和实现简单,适合在真实生产环境中部署与移植.算法基于贝叶斯公式具有较好的理论基础,运行速度较快,适合较大的计算环境,增强了系统的扩展性.
3 评价方法评价指标一般有准确率和ROC曲线(ROC, curve, receiver operating characteristic curve).准确率是给定测试数据集,算法正确预测的样本数与总样本数之比.ROC曲线是根据一系列不同的二分类方式(分界值或决定阈), 以真正率(TPR, true positive rate)为纵坐标, 假正率(FPR, false positive rate)为横坐标绘制的曲线.真正率的计算方法为:被模型预测为正的正样本数除以正样本实际数, 假正率的计算方法为:被模型预测为正的负样本数除以负样本实际数.
4 仿真结果在iVCE真实生产环境中,随机选取平台历史下发的100万个任务执行结果和此时对应计算节点的属性值作为训练样本,即N={30, 60, 90, 120, 150, 180, 210, 240},单位为万个.然后选取10万个历史任务执行结果和此时对应的计算节点的属性值为测试样本,即N′=105.
图 1示出了不同类型任务的预测准确率,基于朴素贝叶斯算的资源预测算法的AUC面积0.959,好于其他几个算法.平台资源可靠性评价通过引入朴素贝叶斯算法,在评价的准确性方面提升了20%以上,通过参数优化算法的准确率同样好于同类其他几个算法2%以上.
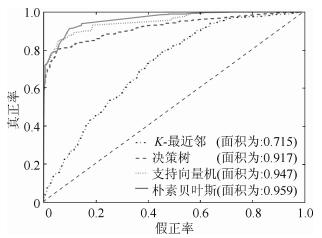
|
图 1 算法间准确率比较 |
图 2示出了算法对平台不同类型资源的预测准确率,以评测算法的鲁棒性和适应性.验证过程中根据文献[5]的思想,对不同类型资源的成功率进行了交差验证,资源的类型基于文献[6]的分类算法.其对不同类型的资源预测结果与预期相符,算法对各种类型的资源都有很好的测试结果.计算类的资源一般性能较高,任务主要在虚拟资源本地计算的任务,其任务的执行成功率相对稳定,算法同样也得到了很高的测试水平.未经明确分类的计算资源,其特点是稳定性较差、资源状态随机性强,难以分类,故平台对其做出了较低的预测结果,另外对网络访问类资源也得到了较高的预测结果,这些资源的特点是具有很好的网络环境,这类资源虽然可能性能不是很高,但有比较稳定的网络访问环境,适应执行一些长时间运行或者对网络要求较高的任务.
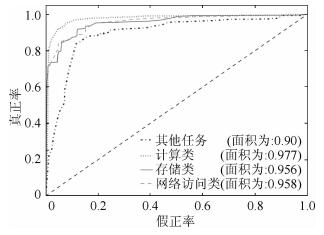
|
图 2 不同类型资源间比较 |
图 3分别示出了各个常见的机器学习算法在本平台上,针对不同大小的数据集所花费的训练时间和测试时间.其中本算法的训练时间比支持向量机(SVM)快3%,但朴素贝叶斯的一个优点是对小数据集,仍然有很高的预测精度.而K最近邻算法训练时间较长,这与K值的选择、距离度量和分类决策规则有关,K近邻没有显示的训练时间,这里K近邻的训练也是指上面三要素的选择过程.算法的预测时间与训练时间比较一致,同样得到了很好的效率.
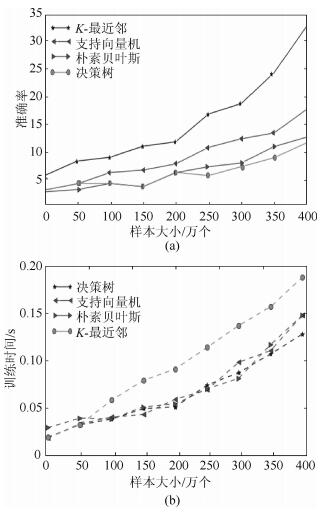
|
图 3 算法间效率比较 |
资源评论是iVCE平台非常重要的工作,是任务成功执行和平台稳定的基础.资源可靠性评价是资源平台的一部分,如何获取资源信息、处理信息和资源如何评价都是非常实际的问题.
笔者提出的基于朴素贝叶斯算法的资源评价模型在实际生产过程中,取得了非常好的效果,算法对资源的特点有非常清楚的把握,使平台的可靠性、扩展性、资源利用率等方面得到显著提高.
| [1] | Lu Xicheng, Wang Huaimin, Wang Ji, et al. Internet-based virtual computing environment(iVCE): concepts and architecture[J]. Science in China, 2006, 49(6): 681–701. |
| [2] | Den X H, Zhang L M, Yi L, et al. A load balance topology of virtual computing environment[J]. Journal of Central South University, 2011, 42(6): 1643–1649. |
| [3] | Prudencio E E, Bauman P T, Faghihi D, et al. A computational framework for dynamic data-driven material damage control, based on Bayesian inference and model selection[J]. International Journal for Numerical Methods in Engineering, 2015, 102(3-4): 379–403. doi: 10.1002/nme.4669 |
| [4] | Araki T, Ikeda K, Akaho S. An efficient sampling algorithm with adaptations for Bayesian variable selection[J]. Neural Networks, 2015, 61: 22–31. doi: 10.1016/j.neunet.2014.09.010 |
| [5] | Wong T T. Performance evaluation of classification algorithms by k -fold and leave-one-out cross validation[J]. Pattern Recognition, 2015, 48(9): 2839–2846. doi: 10.1016/j.patcog.2015.03.009 |
| [6] | Pang S, Ban T, Kadobayashi Y, et al. Personalized mode transductive spanning SVM classification tree[J]. Information Sciences, 2015, 181(11): 2071–2085. |
| [7] | Dehghanpour K, Nehrir M H, Sheppard J W, et al. Agent-based modeling in electrical energy markets using dynamic Bayesian networks[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4744–4754. doi: 10.1109/TPWRS.2016.2524678 |


