2. 中国电子科技集团第五十四研究所 中国通信网信息传输与分发技术 重点实验室, 石家庄 050081;
3. 北京邮电大学 电子工程学院, 北京 100876
针对多技能呼叫中心路由计算的并发性能瓶颈,提出一种并行的呼叫中心路由方法(PCCRM).该方法通过临界资源粒度细化,将互斥范围缩小到局部资源,可显著减少进程间的同步等待,同时引入有序竞争模型来保证算法满足呼叫中心路由基本原则.实验结果表明,PCCRM可以有效提升路由算法的系统处理性能和扩展性.
2. China Electronics Technology Group Corporation 54 th Research Institute, Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China;
3. Electric Engineer School, Beijing University of Posts and Telecommunications, Beijng 100876, China
A parallel routing method named parallel call center routing method(PCCRM) was proposed to promote the multiprocessing performance of call center system with multi-skill model. Through refinement of resource, PCCRM reduced the general mutual exclusion to local mutual exclusion, which can markedly reduce the waiting of process synchronization. Meanwhile an orderly competition model was introduced to guarantee the algorithm to meet the requirement of general principle of call center's agents. The experimental results showed that the PCCRM could increase system performance and scalability of routing algorithm.
云呼叫中心的路由排队算法的扩展性问题是制约呼叫中心云化发展的技术瓶颈.在对多技能组呼叫中心路由分配算法与资源竞争模型分析的基础上,基于分布式互斥方法[1-8]提出一种可以提升路由算法并行程度的并行呼叫中心路由方法(PCCRM,parallel call center routing method). PCCRM方法利用技能队列与座席之间的资源竞争关系,对临界资源粒度进行细化,形成一种基于局部资源互斥的自由竞争模型,可以减少临界区资源占用的数量,提升进程执行路由算法的并行程度.自由竞争模型会破坏路由算法的基本原则,需要引入约束限制,形成有序竞争模型.最后通过实验进行验证和分析.
1 呼叫中心多技能模型呼叫中心座席多技能共享模型如图 1所示,多个技能队列相互之间分享座席资源,座席具备一个或多个技能,在不同的技能中分配不同的等级.

|
图 1 竞争队列集 |
针对要解决的问题,建立呼叫中心多技能路由模型M.
模型M定义:M=(A, S, V),A={ai|1≤i≤N},S={sj|1≤j≤M},V={ vij |1≤i≤N,1≤j≤M},vij =f(ai, sj).满足以下两个约束:
1) ∀vij∈V, vij≥0;
2) ∀ai∈A, 存在一个1≤k≤M和任意的j≠k, 1≤j≤M,使得vik>vij.
其中A为系统中的座席集合,N为系统座席数量,S为系统中技能集合,M为系统技能数量,V为系统中座席和技能的关系,用一个二元组vij=f(ai, sj).其中vij为a在s中的技能等级的数值,如果vij < 0表示座席不具备该技能.模型M的两个约束表示:每个座席a均具有全部的技能,都有且仅有一个主技能.
2 呼叫中心路由算法分析路由算法需从座席状态、座席工作关键性能指标(KPI,key performance indication)数据、座席技能等级以及客户等级、请求的服务等多种维度进行综合考虑,在对座席、客户进行全面的评估基础上,分配一个最佳匹配座席.
2.1 路由算法基本原则1) 工作量公平性原则
该原则考察座席工作量的均衡.策略为根据座席KPI数据,计算一个综合评估值W,从座席集合中取综合值W排序最大的座席为当前分配座席.
综合评估值的计算方法为W=f(p1+ p2+…+ pn),其中pi为KPI数据的归一化值.
2) 服务匹配原则
该原则考虑客户的等级和座席的技能等级匹配性,使用客户请求、客户等级和座席技能信息,指定一个或多个等级座席按优先级来服务.
2.2 路由算法复杂度分析整体算法的时间复杂度可以用O(Kn)表示,其中n代表技能队列对应座席集合的数量,K为根据座席KPI计算综合权值W的时间复杂度,是一个常量.
对于模型M,每个技能覆盖系统全部的座席,因此座席路由计算的时间复杂度为O(K.N),其中N为全部座席的数量.
2.3 并行度分析在多技能模型M中,由于每个技能包含了全部座席,每个技能共享相同的资源,所有的进程在处理路由算法过程时都会竞争同一个资源,算法处理的并行程度为1.
3 PCCRM方法PCCRM方法解决路由互斥算法的性能瓶颈,关键是提升多进程的并行程度,让多个进程可以同时访问座席资源进行路由分配计算.
3.1 多技能建模基于模型M的定义,将技能组作为呼叫中心的基本资源调度单元.呼叫中心按组的多技能路由排队模型可以用一个三元组C=(G,Q,V)来表示.其中G表示系统中的技能组,G中技能组相互没有交集. Q是系统中的技能队列. V代表G和Q关系,表示技能组中座席具有某种技能.
模型C定义:C=(G,Q,V),G={gi|1≤i≤n},Q={qi|1≤i≤m},V={vij|vij=f(gi, qj), vij∈[-1, 0, 1], 1≤i≤n, 1≤j≤m}. VG(gk)={qj|vkj≥0},VQ(qk)={gi|vik≥0},且具有以下约束:
1) 1≤i, j≤n,i≠j,gi∩gj=∅;
2) 1≤i≤n,1≤j≤m,vij≥0,VQ(qj)=G,VG(gi)=Q;
3) 1≤j≤m,存在唯一的i∈[1, n],vij=1.
其中:g组中的座席对技能q存在多种等级,vij≥0表示gi的座席具有技能qj,vij=1表示qj是gi的主技能,主技能的等级是所有组中最高的;VG(gi)表示与技能组gi相关的所有技能队列,即组gi中座席拥有的技能,VQ(qi)表示拥有技能qi的所有技能组.第1个约束表示任意两个技能组没有交集,第2个约束表示任意一个技能组gi均具有全部技能,第3个约束表示每个技能有且仅有一个主技能组.
C的3个约束表明,任意座席只能属于一个组,每个组均具有全技能,且每个组都有一个主要技能.因此模型C符合模型M的要求.
3.2 自由竞争模型自由竞争模型就是进程在访问临界资源的时候,不是一次性地占用全部所需资源,而是逐个对资源加锁访问,当完成某个资源的访问后立即释放资源,让其他的进程可以马上进入临界区.
自由竞争模型中进程的互斥等待造成的影响已经非常小.对资源进行顺序加锁访问时,当每个进程都按照g1→g2→…→gn的顺序对资源进行互斥访问,那么在理想情况下,当多个进程进入稳态运行的时候,多个进程可以并行访问各自资源,无需等待.
此时系统整体计算时间为O((p+r-1)t),p为呼叫数,r为临界资源数量即座席技能分组数,t为临界区资源访问时间复杂度O(Kn),n为技能组座席数量,是系统座席总数N的q分之一(假设均匀分布).那么单个呼叫平均的处理时间为O((p+q-1)NK/pq),随着系统持续运行呼叫量p趋于无穷,平均呼叫处理时间为O(nK),约等于单个临界区执行的时间复杂度,系统并行程度约等于q.
自由竞争模型会产生资源过分占用的情况,导致资源分配破坏路由算法的两大原则.在图 2例子中,进程1在3×t结束时刻完成资源分配,在此之前可能会将g1或g2资源一直占用(临时)直至最后时刻释放,而被进程1临时占用的资源很可能是进程2和3的呼叫最匹配座席,但是却无法分配到进程2和3的呼叫,那么分配给进程2和3呼叫的座席可能不是技能最匹配的,也可能是工作量不是最少的,由此违背了路由算法的两条原则.由于分布式系统执行的不确定性,这种问题有可能会在系统运行中经常发生,导致服务质量下降和分配不均衡,因此不能满足算法的功能性要求.
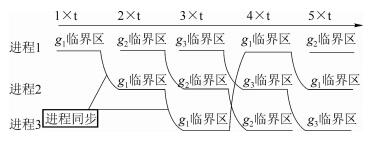
|
图 2 完全竞争的队列 |
由此,需要对自由竞争模型进行约束,以保证路由算法的功能性,即严格遵循座席工作量公平性原则和客服匹配原则.
3.3 有序竞争模型有序竞争模型是在自由竞争模型上添加一些约束,来保证并行方法满足路由算法的两条基本原则.
首先我们提出有序竞争定理:如果在进程按顺序g1g2g3…gn访问临界资源过程中,所筛选的第1个座席就是本次呼叫的最佳匹配座席,那么就不会破坏路由算法的基本原则.
定理很容易证明:如果进程第1个筛选的座席来自于gi,则gi之前的组中都没有匹配的座席,自然不会有资源被临时占用.因此除了gi,其他所有组的座席都没有被临时占用,其他进程可以从除gi之外的组中寻找最匹配座席,不存在资源的过分占用问题和分配冲突.
为了保证路由算法多进程执行能满足有序竞争定理的要求,需要下面几条约束.
第1条约束:每个技能组对应一个技能队列,有且仅有一种技能等级.
第2条约束:任意两个技能组对应同一个技能qii的技能等级是不同的.
第3条约束:路由算法根据呼叫所选的技能,按技能等级由高到低的顺序对具有该技能的技能组进行加锁访问.
根据上述约束,对模型C进行增强.
模型C增强1:增加二元组vij的含义,令vij的数值代表技能组gi拥有技能qj的等级.如vij=9表示gi具有qj的等级为9,vij < 0表示gi不具备技能qi. 即用vij来表示技能组和技能之间的等级.
第2条约束要求一个技能对应的多个技能组拥有不同的等级.
模型C增强2:对于任一队列qk∈Q,0≤k≤m,任意两个vik≥0,vjk≥0,则vik≠vjk.
前两条约束保障了多个技能组对应某个技能的等级是唯一且有序的.
第3条约束则要求进程按照技能等级的顺序在选定技能的多个技能组中有序访问.如果座席路由算法优先考察技能和等级匹配情况,则该约束可以保障进程总是优先去查看最匹配的技能等级座席.
为了满足有序竞争定理要求,还需要增加一条针对路由算法的约束,即座席分配须按技能等级为优先级进行遴选.
第4条约束:对路由策略的约束,设定路由策略为优先分配技能等级高的座席.
4 算法复杂度分析有序竞争模型对技能组按技能和等级排序,通过约束路由算法的按技能等级高低顺序访问技能组,因此存在最佳情况和最坏情况.
在最佳情况下,每个技能队列都只需访问最佳匹配技能组,即可获得最佳匹配座席.假设座席分组和呼叫请求都均匀分布,则单个呼叫的计算复杂度为O(K.l),l为队列长度.进程并行程度可达到m,m等于技能组数量.系统整体的呼叫处理时间复杂度达到O(Kl/m).
最坏的情况下,所有呼叫需要访问全部的临界资源,单个呼叫的计算复杂度为O(KN).一般情况,这种最坏情况出现的概率非常低,要求从技能队列qk对应的组gk1到gkn都没有匹配的座席,而且所有队列都没有进入排队(排队状态下呼叫直接进入队列).这是一个系统临界状态,任何一个呼叫的到来或座席的状态变化,都会打破这种状态.所以最坏的计算复杂度O(KN)在实际运行中只会短暂存在.
5 实验验证在实验中启动了4个进程模拟执行路由算法,包括4个技能组和4个技能队列,每个技能组拥有4个技能,每个技能的多个组具有不同的等级.
对3种模型进行模拟对比,实验实现方法如下.
1) 普通模型:采用未经优化的分布式互斥算法,设置一个统一的互斥变量.
2) 自由模型:采用自由竞争模式优化的互斥算法,每个进程按固定顺序对技能组进行加锁互斥访问.
3) 有序模型:采用有序竞争模式优化的互斥算法,按每个技能的等级顺序对技能组加锁互斥访问.
通过表 1和图 3实验数据的对比分析发现,未经优化的互斥方法相当于是串行执行,需要的处理时间最多,算法处理性能几乎没有提升.有序模型的全部局部资源访问模式下的并行程度和性能与自由竞争模型非常接近,性能损失很少,而部分局部资源访问模式下,性能远远高于自由竞争模型.因此,有序竞争模型在绝大部分的情况下可以对呼叫中心路由算法的性能有明显的提升.
|
|
表 1 试验结果数据 |
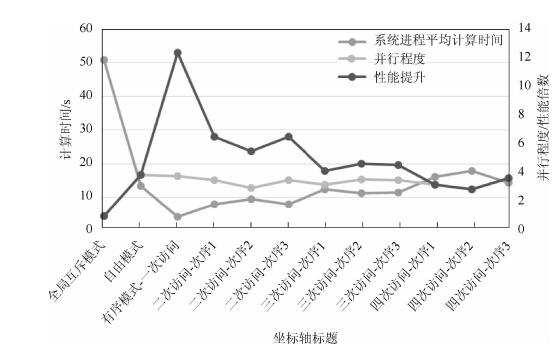
|
图 3 实验数据对比 |
多技能模型呼叫中心的座席资源竞争和互斥访问导致系统性能扩展性不佳是实际问题. PCCRM通过资源粒度细化和有序竞争约束,提高了资源利用率和进程并行程度.虽然引入了若干限制,但是没有违反路由算法的基本准则和多技能共享模型要求,在实际应用中不会产生限制.
| [1] | Lamport L. Time, clocks and the ordering of the events in distributed system[J]. Communications of the ACM, 1978, 21(7): 558–565. doi: 10.1145/359545.359563 |
| [2] | Lamport L. The part-time parliament[J]. ACM Transaction of Computer System, 1998, 16(2): 133–169. doi: 10.1145/279227.279229 |
| [3] | Lamport L. Paxos made simple[J]. ACM SIGACT News, 2001, 32(4): 51–58. |
| [4] | Maekawa M. A sqrt(n) algorithm for mutual exclusion in decentralized systems[J]. ACM Transactions on Computer Systems, 1985, 3(2): 145–159. doi: 10.1145/214438.214445 |
| [5] | Ng W K, Ravishankar C V. Coterie templates-a new quorum construction method[C]//Proceedings of the 15th International Conference on Distributed Computing System.Vancouver, BC:IEEE Press, 1995: 92-99. |
| [6] | Li Meian, Liu Xinsong, Wang Zheng, et al. A symmetric quorum algorithm for distributed mutual exclusion based on the properties of cyclic quorum[J]. Chinese Journal of Electronics, 2006, 1(1): 17–20. |
| [7] | Baldoni R, Virgillito A, Petrassi R. A distributed mutual exclusion algorithm for moblie Ad-Hoc networks[J]. International Journal of Computer Networks & Communications, 2012, 413(1): 539. |
| [8] | Lejeune J, Arantes L, Sopena J, et al. A fair starvation-free prioritized mutual exclusion algorithm for distributed systems[J]. Journal of Parallel & Distributed Computing, 2015(83): 13–29. |


