2. 北京邮电大学 信息安全中心, 北京 100876
提出了一种非下采样剪切波变换域下的分块数字水印算法,充分利用了非下采样剪切波变换中的方向性特征,并选用信息熵作为选择图像中待嵌入块的标准,应用奇异值分解的方法进行水印信息的嵌入,解决了多尺度分析水印算法中不可见性和鲁棒性不能兼顾的问题.实验结果表明,提出算法中峰值信噪比高于51 dB,归一化相关系数均高于0.93,其性能得到了较大的提高.
2. Information Security Center, Beijing University of Posts and Telecommunications, Beijing 100876, China
A novel block-based digital watermarking scheme in non-subsampled shearlet transform was proposed. The directional features of the NSST was utilized and the entropy was taken as the criterion of selecting the embedded blocks in images. Besides, this scheme applied singular value decomposition to embed the binary watermark logo. The algorithm not only solved the problem that the invisibility and the robustness in multiscale analysis watermarking algorithm could not be taken into account, but also fully showed the superiority comparing with other previous schemes. Experiment results demonstrated that the peak signal to noise ratio was above 51 dB and most of normalized correlation values were higher than 0.93. The imperceptibility and robustness performance was experimentally proved to be enhanced.
随着网络技术的快速发展,数字水印已成为一种保证数据完整性和知识产权的关键技术[1],其必须满足不可见性、鲁棒性等要求.近几年,Guo和Labate提出的具有多尺度和多分辨率特点的剪切波变换很好地表征了多维信号本身的几何特性,而且描述了图像边缘的方向性信息.
通过长期研究剪切波变换理论及相关水印算法[2], 并在此基础上提出了一种基于非下采样剪切波变换(NSST, non-subsampled shearlet transform)和奇异值分解(SVD, singular value decomposition)的水印算法.采用二值图像作为水印信息,对原始图像进行分块,选择信息熵较大的3个图像块进行非下采样剪切波变换,确定高频方向细节子图进行奇异值分解,最后将水印图像嵌入到奇异值中.通过大量的仿真实验,该算法具有较好的不可见性和鲁棒性.
1 剪切波和奇异值分解理论 1.1 剪切波变换具有合成膨胀的二维仿射系统[3]定义如下:
| $ \begin{array}{l} {\psi _{ast}}\left( x \right) = \{ {a^{-3/4}}\psi (A_{_a}^{^{-1}}B_{_s}^{^{-1}}\left( {x - t} \right)), \\ a \in {R^ + }, s \in R, t \in {R^2}\} \end{array} $ | (1) |
其中:ψ∈L2(R2)是合成膨胀二维仿射系统的元素;
连续剪切波变换具有如下定义:
| $ {S_f}\left( {a, s, t} \right) = \left\langle {f, {\psi _{ast}}} \right\rangle $ | (2) |
其中a、s和t分别是尺度参数、剪切参数和平移参数.
| $ \begin{array}{l} {\rm{Supp}}\;{{\hat \psi }_{ast}} \subset \{ ({\xi _1}, {\xi _2}):{\xi _1} \in [-2/a, -1/(2a)] \cup \\ [1/\left( {2a} \right), 2/a, |s + {\xi _2}/{\xi _1}| \le \sqrt a \} \end{array} $ | (3) |
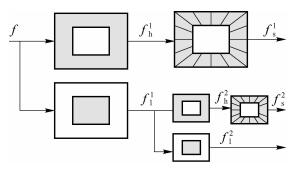
非下采样剪切波变换[4-5]主要分为非下采样拉普拉斯金字塔分解和方向滤波器2个过程.非下采样剪切波变换的结构图如图 1所示.在图 1中,f表示输入的原始图像,fh1和fl1分别表示图像经过第1层拉普拉斯金字塔分解后得到的高频图像,低频图像;fs1表示该高频图像经过第1层方向分解后得到的方向子带图.fh2和fl2分别表示上述低频图像经过第2层拉普拉斯金字塔分解后得到的高频图像,低频图像;fs2表示该高频图像经过第2层方向分解后得到的方向子带图.
|
图 1 非下采样剪切波中滤波器的实现 |
在提出算法中,考虑到人类视觉特性对图像平滑区域的变化相对于边缘纹理区域的变化较为敏感,即对图像的边缘区域能够允许较大的干扰信息,将水印嵌入到图像中的平滑区域会影响算法的不可见性,因此选择先将图像分成平滑区和非平滑区.而熵是图像所具有的一种度量方式,熵值越大,说明该部分含有的信息就越丰富;将水印嵌入到信息熵最大(边缘信息最为丰富)的图像块中,可以保证算法的不可见性较好.
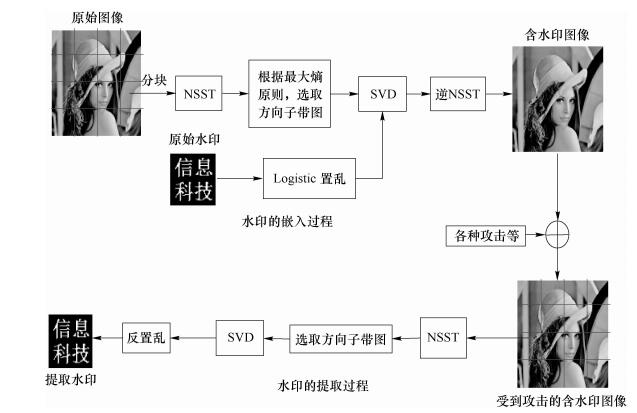
该图像块经过具有平移不变特性的非下采样剪切波变换,分解成低频近似子图和多个具有不同分辨率,不同方向的高频细节子图,选择信息熵最大的高频方向子带作为嵌入位置.另外,由于奇异值的稳定性且其代表了矩阵的几何属性等特点,当水印嵌入到方向子带奇异值中并对含水印矩阵进行各种攻击和常规图像处理操作时,对奇异值的影响较小,因此保证了算法的鲁棒性,其嵌入和提取过程如图 2所示.
|
图 2 水印的嵌入与提取过程 |
数字水印的嵌入过程如下所述.
1) 将原始图像分成与水印图像大小相同的不重叠的块,选取信息熵较大的3个图像块作为待嵌入块;
2) 对待嵌入块进行2层非下采样剪切波变换,得到表征图像不同方向细节的子图;
3) 选取信息熵最大的方向子带图,标记为subbando,并进行奇异值分解,公式为
| $ [{U_{\rm{o}}}, {S_{\rm{o}}}, {V_{\rm{o}}}] = {\rm{svd(subban}}{{\rm{d}}_{\rm{o}}}{\rm{)}} $ | (4) |
其中:Uo、So和Vo分别表示原始子带图分解后得到的左奇异值向量、奇异值矩阵和右奇异值向量.
4) 利用Logistic映射对原始水印w进行置乱加密;
5) 通过水印信息改变方向子带图的奇异值,得到新的矩阵信息,标记为Sw,即
| $ {S_w} = {S_o} + aw $ | (5) |
其中:a表示嵌入强度,w表示置乱后的水印信息.
6) 对Sw进行奇异值分解,得到含有水印信息的奇异值,标记为S′w,即
| $ [U{^{\prime} _{\rm{w}}}, S{^{\prime} _{\rm{w}}}, V{^{\prime} _{\rm{w}}}] = {\rm{svd}}({S_w}) $ | (6) |
7) 通过下述公式得到新的系数块,即
| $ {\rm{block}}^{\prime} = {U_{\rm{o}}}S{^{\prime} _{\rm{w}}}V_{\rm{o}}^{^{\rm{T}}} $ | (7) |
8) 进行非下采样剪切波逆变换得到含水印的重构图像.
2.3 水印的提取算法数字水印的提取过程如下所述.
1) 根据信息熵原则选取图像块,对其进行2层非下采样剪切波变换后,选择方向子带图作为待提取块,标记为subband.
2) 对待提取块进行奇异值分解,即
| $ [{U_{\rm{r}}}, {S_{\rm{r}}}, {V_{\rm{r}}}] = {\rm{svd(subband)}} $ | (8) |
其中Ur、Sr和Vr分别表示待提取子带图分解后得到的左奇异值向量、奇异值矩阵和右奇异值向量.
3) 根据下述公式得到置乱的水印信息,即
| $ S{^{\prime} _{\rm{r}}} = U{^{\prime} _w}{S_{\rm{r}}}V{^{\prime}} _w^{^{\rm{T}}} $ | (9) |
| $ w^{\prime} = (S{^{\prime} _{\rm{r}}}-{S_{\rm{o}}})/a $ | (10) |
4) 对置乱的水印信息进行解密,提取出水印.
通过上述步骤,提取出完整的水印信息.
3 实验结果与分析使用标准图像库中提供的多幅图像进行了大量的仿真实验,证明了提出算法中数字水印具有很好的不可见性和鲁棒性.以3幅512×512大小的图像(“Lena”“Baboon”“Goldhill”)作为原始图像进行实验数据的说明,水印图像是大小为64×64的二值图像.
3.1 水印的不可见性采用峰值信噪比(PSNR, peak signal to noise ratio)作为数字水印算法中不可见性的性能评价标准,用归一化相关系数(NC, normalized correlation)作为水印算法中鲁棒性的性能评价标准.嵌入水印后的图像和提取水印,相应的PSNR值和NC值如图 3所示.

|
图 3 含水印图像和提取水印 |
实验结果表明,在未受到攻击时,原始图像与嵌入水印后的图像之间的PSNR达到51 dB以上,说明嵌入水印后的图像的质量较好,人眼无法察觉这幅图像是否有水印嵌入,满足水印的不可见性;并且提取的水印质量较好,与原始水印几乎无差异,NC值均接近为1,满足水印的鲁棒性.
3.2 水印的鲁棒性在验证水印鲁棒性实验中,测试了含水印图像受到滤波、JPEG压缩、旋转、噪声等攻击后的PSNR值和NC值,并给出了相应的含水印图像和提取水印图像.
1) 不同攻击下的鲁棒性
表 1显示了含水印图像受到平滑、缩放、JPEG压缩等攻击后的PSNR和NC值.
|
|
表 1 不同攻击后的水印提取效果 |
从表 1的数据可知,图像受到平滑、比例缩放和JPEG压缩攻击后,其PSNR值多高于30 dB,表明图像间的视觉差异非常小,攻击后的图像质量较好;当图像受到平滑、缩放和旋转攻击后,其NC值多高于0.97,能提取出较完整的水印并被人眼所感知,但当Baboon图像受到JPEG压缩攻击后,其NC值约为0.93,仍具有较高的可辨识度.实验结果表明,提出算法对上述攻击具有较好的鲁棒性.
2) 噪声攻击下的鲁棒性
表 2显示了含水印图像受到不同方差的高斯噪声和不同密度的椒盐噪声后的PSNR和NC值.
|
|
表 2 添加噪声后的水印提取效果 |
从表 2的实验数据可知,随着高斯噪声的方差和椒盐噪声的密度逐渐变大,造成图像之间的PSNR值逐渐减小,含水印图像的质量降低,但仍高于20 dB.图像受到高斯噪声后,NC值随着噪声方差的增大也逐渐减小,但仍高于0.95;对Lena和Goldhill图像,其受到椒盐噪声后,NC值均高于0.99;但Baboon图像受到椒盐噪声后相对来说抗攻击能力不太稳定,NC值约为0.9.实验结果表明,提出算法对噪声攻击具有较好的鲁棒性.
3) 剪切攻击下的鲁棒性
图 4显示出剪切掉大小为128×128的图像块后,其含水印图像和提取的水印图像以及相应的PSNR和NC值.

|
图 4 含水印图像和提取水印 |
从图 4可看出,当剪切掉熵最大的图像块时,从其他嵌入块中提取的水印图像也具有很好的辨识度,NC值高于0.92,因此提出算法对剪切攻击具有较好的鲁棒性.
4) 不同攻击下的性能
图 5显示了在比例缩放、剪切、高斯噪声等攻击下的含水印图像和提取的水印.

|
图 5 受到攻击后的含水印图像和提取的水印 |
从图 5中可以看出,Lena图像受到缩放、均值滤波、椒盐噪声等不同的攻击后能提取出质量较好的水印图像;对于剪切攻击和高斯噪声攻击则效果不太稳定,但提取的水印仍较为完整,说明提出算法对上述攻击具有较好的鲁棒性.
3.3 算法性能比较为了进一步说明提出算法对中值滤波、高斯噪声、低通滤波、椒盐噪声、JPEG压缩和旋转等攻击的鲁棒性性能,将所提出算法与文献[6-7]中的方法进行比较,如表 3所示.
|
|
表 3 Lena图像不同变换域下的算法性能比较 |
由表 3可以看出,提出算法对低通滤波和JPEG压缩攻击的鲁棒性与文献中的算法鲁棒性相当,对旋转和噪声等攻击,提出算法的NC值明显高于文献[7]中的数值,并且对于上述攻击其NC值均大于0.95,具有较好的鲁棒性.
4 结束语提出了一种新的基于非下采样剪切波变换和奇异值分解相结合的鲁棒性数字水印算法.该算法充分利用了剪切波变换多尺度和多方向分解特点,并选取信息熵较大的3个图像块进行剪切波变换,利用奇异值分解方法进行水印信息的嵌入.实验结果表明,原始图像和含水印图像间的PSNR达到51 dB以上,且经过旋转、剪切、滤波、噪声等攻击后仍能提取出完整的水印,因此提出算法具有较好的不可见性和鲁棒性.
| [1] |
林威, 翟信德, 朱长青, 等. 基于QR码的遥感影像数字水印算法[J]. 北京邮电大学学报, 2015, 38(1): 26–30.
Lin Wei, Zhai Xinde, Zhu Changqing, et al. QR code based research on digital watermark algorithm for remote sensing image[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(1): 26–30. |
| [2] | Zhao Jian, Sun Meiling, Jia Jian, et al. Image watermark based on extended shearlet and insertion using the largest information entropy on horizontalcCone[J]. Mathematical Problems in Engineering, 2015(3): 1–10. |
| [3] | Easley G, Labate D, Lim W Q. Sparse directional image representations using the discrete shearlet transform[J]. Applied and Computational Harmonic Analysis, 2008, 25(1): 25–46. doi: 10.1016/j.acha.2007.09.003 |
| [4] | Gao Guorong. Image denoising by non-subsampled shearlet domain multivariate model and its method noise thresholding[J]. Optik—International Journal for Light and Electron Optics, 2013, 124(22): 5756–5760. doi: 10.1016/j.ijleo.2013.04.014 |
| [5] | Wang Xiangyang, Liu Yunan, Li Shuo, et al. Robust image watermarking approach using polar harmonic transforms based geometric correction[J]. Neurocomputing, 2016, 174(PB): 627–642. |
| [6] | 金献珍. 基于图像加密和奇异值分解的小波域数字水印算法研究[D]. 杭州: 浙江工业大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10337-2009202270.htm |
| [7] | Narasimhulu C V, Prasad K S. A new SVD based hybrid color image watermarking for copyright protection using contourlet transform[J]. International Journal of Computer Applications, 2011, 20(8): 18–27. doi: 10.5120/ijca |


