2. 北京邮电大学 网络与交换技术国家重点实验室, 北京 100876
基于协作干扰机制,研究了分布式无线网络中,节点采取怎样的交互与合作策略能提升其物理层安全传输性能.该问题被建模成一个联盟形成博弈,并引入享乐设置,在此基础上提出一种分布式享乐博弈算法,以获取稳定的联盟结构.仿真结果表明,相比于非合作及基于放大转发的博弈机制,所提出的合作博弈机制可以大幅提高网络用户的平均安全传输性能.
2. State Key Laboratory of Network and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
The interaction and cooperation strategies among sources and friendly jammers to improve their secrecy capacity with physical layer security in a practical decentralized wireless network are investigated. The problem was formulated as a hedonic coalition formation game, and then a distributed hedonic coalition formation algorithm was proposed to achieve the stable coalition. Simulation results showed the proposed scheme could significantly improve the average payoffs per user comparing with the non-cooperative case and the amplify-and-forward case.
在物理层安全理论中,当源-目的信道(即主信道)差于源-窃听者信道时,源节点无法获得非零的保密速率[1],为此,节点协作成为克服以上安全通信瓶颈的有效方法[2-5].例如,Khisti等[2-3]分别研究了解码转发(DF)与放大转发(AF)两种经典协作协议下的保密速率收益.另一种提升保密速率的协作策略被称为协作干扰(CJ)[4-5],它是指协作节点通过扮演友好干扰点的角色,以干扰源-窃听者信道,从而提高主信道传输的私密性.上述基于节点协作的工作均以网络中所有的节点都愿意参与合作为前提.
区别于现有的工作,在协作干扰的背景下,试图从整个网络的角度找到一个“最优”的合作结构,以尽可能大地提升网络中所有源节点的保密速率.通过将上述问题建模为联盟博弈模型[6],并进一步根据享乐博弈提出一种分布式享乐结盟算法,使得网络中的多个源节点及友好干扰节点能够自主形成一个收敛的、稳定的联盟结构.仿真结果表明,每个源节点与联盟内的干扰点合作时获得的保密速率,将比不合作下的直接传输以及AF下的联盟博弈机制[7],分别提升约14.29%和10.73%.
1 系统模型与问题建模 1.1 网络模型考虑一个网络中有源节点集合N,分别向目的节点集合D传输数据,同时网络中存在一个窃听节点E,试图窃听源节点的信息.此外,有协作节点集合Τ在网络中扮演友好干扰点的角色,当与之合作的源节点i∈N传输数据时,一组干扰节点集合Si⊆Τ将共同发射独立于信源的“噪声”信号,以干扰窃听者,提高源节点传输数据的保密性,即保密速率.与文献[7]类似,考虑时分多址接入系统(TDMA, time division multiple access),即每个源节点i∈N在其分配的时隙内向它们的目的节点传输各自数据.源节点可以单独地向目的节点传输数据,也可以在需要的时候向1个或者多个干扰节点寻求帮助,以CJ的方式传输数据,从而形成一组合作联盟.定义每个时隙的长度为θ,且时分系统每个时隙的总功率约束为P.
在不合作的情形下,一个源节点i∈N在其所占用的时隙内向目的节点i∈N发送数据所能获得的最大的可靠传输速率,即保密速率,定义为[1]
| $ {C_{i, {D_i}}} = {\left( {{R_{i, {D_i}}}-{R_{i, E}}} \right)^ + } $ | (1) |
其中:Ri, Di与Ri, E分别是源节点i到目的节点Di及窃听者E的信道速率,(X)+表示其数值取为max(0, X).因此,有
| $ {R_{i, {D_i}}} = B\;{\rm{lb}}\left( {1 + {{\left| {{h_{i, {D_i}}}} \right|}^2}P/{\sigma ^2}} \right) $ | (2) |
| $ {R_{i, E}} = B\;{\rm{lb}}\left( {1 + {{\left| {{h_{i, E}}} \right|}^2}P/{\sigma ^2}} \right) $ | (3) |
其中:B代表信道带宽,hi, Di和hi, E分别代表相应节点间的信道,这里假定所有信道的噪声功率一样,记为σ2.特别地,式(2) 和式(3) 表明,在独占时隙的情况下,所有的功率P都作为源节点i的发射功率.
为了提升保密速率,源节点将与网络中的友好干扰点进行合作,形成协作干扰联盟S.一旦需要与网络中存在的一些干扰点合作,类似于文献[7]中的机制,在i传输数据前,需要事先与处于同一联盟中的干扰点进行信息交互:在第1阶段,i需要广播它的合作信息(控制,信道等)给潜在联盟中的合作者,假设i把上述需要的信息压缩成一个L bit长度的广播包来发送;第2阶段,当所有的合作干扰点收到广播信息后,i传输数据,同时干扰点根据得到的信息分配干扰功率,进行协作干扰(CJ).因此,信息交换阶段所耗费的功率是Pi, j′=γσ2/|hi, j′|2,γ表示信息交换的目标信噪比,|hi, j′|2是源节点到最远干扰点j∈S∩T间的路径损耗.这样的话,在联盟S所属的时隙内,可以用于CJ阶段发射源信号及干扰信号的剩余功率为PiS=(P-Pi, j′)+.
在CJ阶段,干扰点发射“噪声”试图干扰窃听者的接收信号质量,但是,该噪声同时也影响了源节点发送的有效信息.因此,在CJ情形下,源节点i所能获得的保密传输速率定义为
| $ C_{_{i, {D_i}}}^{^S} = (1-{\eta _i}){\left( {R_{_{i, {D_i}}}^{^S}-R_{_{i, E}}^{^S}} \right)^ + } $ | (4) |
其中系数(1-ηi)代表有ηi部分的时隙已经用于第1阶段的信息交换.引入友好干扰噪声后,有
| $ R_{_{i, {D_i}}}^{^S} = B\;{\rm{lb}}\left( {1 + {P_i}{{\left| {{h_{i, {D_i}}}} \right|}^2}/({{\left| {\mathit{\boldsymbol{W}}_{_S}^†{\mathit{\boldsymbol{h}}_{j, {D_i}}}} \right|}^2} + {\sigma ^2})} \right) $ | (5) |
| $ R_{_{i, E}}^{^S} = B\;{\rm{lb}}\left( {1 + { {{P_i}{\left|{h_{i, E}}\right|} }^2}/({{\left| {\mathit{\boldsymbol{W}}_{_S}^†{\mathit{\boldsymbol{h}}_{j, E}}} \right|}^2} + {\sigma ^2})} \right) $ | (6) |
其中:Pi为源节点i的发射功率,j∈T代表i所属联盟S中的合作干扰点(共有(|S|-1) 个),在式(5) 和式(6) 中,干扰点到目的节点与窃听者的信道记为(|S|-1)×1的列向量h.WS†表示分布在|S|-1个干扰点天线上的干扰功率权重矢量的共轭转置.显然,所有的干扰功率之和必须小于等于PiJ=PiS-Pi.
Dong等[4]在研究中指出,借助波束形成技术,当干扰点发射的噪声之和等于PiJ,且干扰噪声在目的节点Di处被完全抵消,即WS†hj, Di=0时,可以得到最大化保密速率的WS与Pi的闭式解,即
| $ W_{_S}^{^{{\rm{opt}}}} = {\mu _S}\sqrt {P_{_i}^{^S}-{P_i}} \left( {{{\left\| {{\mathit{\boldsymbol{h}}_{j, {D_i}}}} \right\|}^2}{\mathit{\boldsymbol{h}}_{j, E}}-\mathit{\boldsymbol{h}}_{_{j, {D_i}}}^†{\mathit{\boldsymbol{h}}_{j, E}}{\mathit{\boldsymbol{h}}_{j, {D_i}}}} \right) $ |
其中‖a‖表示向量a的二项式范数,且
此外,在|S|=2的情况下,由于只有一个干扰点工作,无法使用波速成形技术将目的节点处的干扰噪声置0.为此,把式(5) 和式(6) 中的噪声向量表达式WS†hj, Di和WS†hj, E分别替换成只有单个干扰点情形下的PiJ|hj, Di|2与PiJ|hj, E|2,根据PiJ =PiS-Pi,重新对式(6) 求导,可以直接得到最优的干扰功率解PiJ,即一个一元二次方程的根.
最后,给出式(4) 中ηi的定义.注意到在信息交换阶段,窃听者E同样能窃听到来自源节点i的广播信息,为此,该阶段源节点能够达到的最大保密传输速率为
| $ \begin{array}{l} {C_{i, j\prime }} = B({\rm{lb}}(1 + {P_{i, j\prime }}{\left| {{h_{i, j\prime }}} \right|^2}/{\sigma ^2})-\\ {\rm{lb}}(1 + {P_{i, j\prime }}{\left| {{h_{i, E}}} \right|^2}/{\sigma ^2}){)^ + } \end{array} $ | (7) |
因此,对长度为L bit的广播数据包来说,广播信息所花费的时隙长度可以定义为θi, j′=L/Ci, j′,显然的,有ηi=θi, j′/θ.
1.2 联盟博弈建模首先,讨论网络节点的收益.对干扰点而言,付出部分功率协助源节点i,相应地,每个干扰点j声明一个单位功率的价格λj,向同联盟的向其请求合作的源节点i收取费用.因此,对任意一个干扰点j∈S,其效用函数vj(S)定义为
| $ {v_j}\left( S \right) = \left\{ \begin{array}{l} {\lambda _j}|W_{S, j}^{{\rm{opt}}}{|^2}, \; 如果 |S| > 2\\ {\lambda _j}P_i^J, \;\; 如果 |S| = 2\\ 0, \;\;其他 \end{array} \right. $ | (8) |
其中WS, jopt表示最优权重向量WSopt的第j个分量.进一步,对每个源节点i∈S,其效用函数vi(S)可定义为
| $ {v_i}\left( S \right) = C_{_{i, {D_i}}}^{^S}-\mathop \sum \limits_{j \in S} {v_j}\left( S \right) $ | (9) |
对所研究的基于CJ的物理层安全传输模型来说,可以很直观地对博弈的参与者N∪T定义一个如下的映射.
| $ \left. \begin{array}{c} V\left( S \right) = \{ \varphi \left( S \right) \in {{\bf{R}}^{\left| S \right|}}|\varphi \left( S \right) = \\ -\infty, 如果 S = \{ i, i', {S_i}\} 或 \\ P_i^S = 0||{\eta _i} \ge 1\\ 且 {\varphi _i}\left( S \right) = {v_i}\left( S \right){\varphi _i}\left( S \right) = \\ {v_i}\left( S \right), \forall i, j \in S, 其他 .\} \end{array} \right\} $ | (10) |
注意到,为了防止一个联盟中出现1个以上的源节点,诸如i,i′,定义这种情况下的所有联盟成员的收益均为负无穷,即该联盟不可能形成.
为了求解上述联盟形成问题,借用享乐博弈[6]的概念.每个博弈参与者n能够对所有它可能属于的联盟集合建立一个完备的、自反的、可传递的偏好关系用
| $ {S_\alpha }{\succeq _n}{S_\beta } \Leftrightarrow {f_n}({S_\alpha }) \ge {f_n}({S_\beta }) $ | (11) |
其中Sα, Sβ⊆N∪T是任意2个包含参与者n的联盟,即n∈Sα且n∈Sβ.fn则是对任意用户n∈N∪T所定义的偏好函数.根据网络模型的特点,提出一种“严进宽出”(FX-AE,free exit-approved entry)偏好.正式地,基于FX-AE的偏好函数可以定义为
| $ {f_n}\left( S \right) = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {}&{}\\ {{\varphi _n}\left( S \right),}&\begin{array}{l} 如果 \left( {{\varphi _m}\left( S \right) \ge {\varphi _m}( {S\backslash \{ n\} } } \right),\\ \forall m \in S\backslash \{ n\} \\ \& S \notin q\left( n \right)) 或 (|S| = 1) \end{array}\\ {}&{} \end{array}\\ - \infty ,\;\; 其他 \end{array} \right. $ | (12) |
其中:φn(S)为联盟S中的用户n的收益,由式(10) 给出.类似地,φm(S)指的是将要进入的新联盟的用户收益. q(n)是一个历史记忆集,表示用户n曾经访问过但是后来又离开的联盟.设置q(n)的目的是为了避免用户在联盟之间频繁地跳跃,提高博弈的效率.
2 分布式享乐博弈算法把这个由多个小联盟组成的结构定义为一个联盟分割,H={S1, S2, …, Sr},且∪k=1rSk=N∪T.
定义1 享乐换位准则.给定一个对N∪T的联盟分割H={S1, S2, …, Sr},任何一个参与者n∈N∪T决定离开它当前所属于的联盟SH(n) =Sk,其中k∈{1, 2, …, r},并加入另一个联盟Sg∈H∪{∅},当且仅当Sg∪{n}≻nSH(n).于是,{Sk, Sg}→{Sk\{n}, Sg∪{n}}从而H → H′,其中H′表示每次独立的享乐换位操作后产生的新联盟分割.
基于此规则,可以建立如下的分布式享乐博弈算法.
步骤1 邻居搜索.每个源节点i通过第1节描述的机制依次在它的分配时隙内搜索邻居干扰点,可以认为所有参与者n将获得Hinitial={S1, S2, …, Sr}.
步骤2 对每个博弈参与者n∈N∪T,给定当前的联盟结构Hcurrent,特别地,在第1轮,Hcurrent=Hinitial.
步骤3 每个参与者n根据(12) 所定义的偏好函数,调查可能的享乐换位操作,如果可行的话,则n把当前联盟加入其个人历史记忆集合q(n),即更新q(n).之后离开当前联盟,并加入满足偏好关系的新联盟.
步骤4 迭代上述步骤,直至收敛于一个稳定的联盟结构Hfinal.
3 仿真与分析为了验证上述机制的有效性,在Matlab中建立一个2 km×2 km的网络.假设每个源节点都向离它最近的目的节点Di∈D发射数据,同时,网络中任意两点间的信道均采用视距信道模型,例如hi, Di=di, Di-α/2eφi, Di表示源节点i到其目的节点Di的信道,其中di,Di表示两者间的距离,α=3.5是路径损耗指数,φiDi是随机相位,信道带宽B取100 kHz.
图 1给出了存在两个目的节点时的稳定合作场景实例,其中相同颜色的源节点与干扰点表示处于同一个合作联盟.例如,源节点7直接向D2节点传输数据即能获得1.083 6×105的非零效用,但是源节点7最终选择与19、21、46这3个干扰点合作,尽管这意味着7需要向它们支付一定的费用,但是通过3个节点的协作干扰,最后源节点7的效用可以提升至1.809 8×105,而3个干扰点也能从0收益变为分别获得237.7、45.444 6、14.430 7的效用,从而7、19、21、46组成了一个协作干扰联盟.

|
图 1 10个源节点40个干扰点下的稳定合作结构 |
图 2给出了源节点平均收益值的比较.随着网络中节点数目的增加,协作干扰机制下的源节点收益将不断递增,这是由于源节点有更多的机会找到更好的合作干扰点.此外,协作干扰下的源节点收益一直大于非合作及放大转发情形下的收益,在节点总数达到100个时(10个源节点,90个干扰点),相比于非合作以及文献[7]提出的基于AF下联盟博弈机制,笔者所提出的协作干扰方案可以将网络用户的平均安全传输性能分别提升约14.29%和10.73%.

|
图 2 协作干扰与直接传输的源节点平均收益比较(蒙特卡洛实验) |
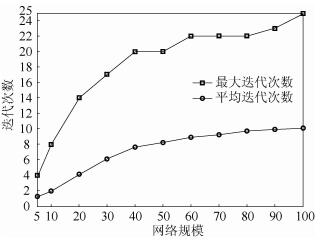
最后,讨论提出算法的收敛速度与性能.图 3给出了不同网络规模下算法收敛于稳定联盟结构所需要的最大迭代次数与平均迭代次数.可以看出,随着网络节点数目的增加,整体而言,迭代次数是不断增加的,这是由于节点数目的增加提高了节点合作的机会,因此,需要经历更多的换位尝试与操作.注意到,当网络规模已经达到100个时,平均迭代次数约为10次,且平均迭代次数呈现愈加平缓的趋势,从而说明所提出的算法在收敛时间或速度上是合理而适当的.
|
图 3 不同网络规模下算法的最大迭代次数与平均迭代次数 |
针对分布式无线网络中的节点协作干扰机制开展研究,提出了一种基于协作干扰的联盟博弈模型,用于分析在引入实际合作代价情形下的节点安全传输问题.通过引入享乐设置,进一步提出了一种分布式享乐博弈算法,得到稳定的基于协作干扰的联盟合作结构.仿真结果表明,相比于非合作与放大转发博弈[7]的情形,上述机制可以将网络用户的安全传输性能分别提升约14.29%和10.73%.
| [1] | Khisti A, Wornell G W. Secure transmission with multiple antennas: The MISOME wiretap channel[J]. IEEE Transactions on Information Theory, 2010, 56(7): 3088–3104. doi: 10.1109/TIT.2010.2048445 |
| [2] | Dong Lun, Han Zhu, Petropulu A P et al. Secure wireless communications via cooperation[C]//46th Annual Allerton Conference on Communication, Control, and Conputing. Urbana-Champaign: IEEE, 2008: 1132-1138. |
| [3] | Dong Lun, Han Zhu, Petropulu A P, et al. Amplify-and-forward based cooperation for secure wireless communications[C]//IEEE ICASSP. Taipei: IEEE, 2009: 2613-2616. |
| [4] | Dong Lun, Han Zhu, Petropulu A P, et al. Improving wireless physical layer security via cooperating relays[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1875–1888. doi: 10.1109/TSP.2009.2038412 |
| [5] |
雷维嘉, 战美慧, 谢成静, 等. 能量协作网络中基于协作干扰的物理层安全方案[J]. 北京邮电大学学报, 2015, 38(6): 65–68.
Lei Weijia, Zhan Meihui, Xie Chengjing, et al. A physical layer security scheme based on cooperative jamming in energy cooperation networks[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(6): 65–68. |
| [6] | Saad W, Han Zhu, Debbah M, et al. Coalitional game theory for communication networks: a tutorial[J]. IEEE Signal Processing Magazine, 2009, 26(5): 77–97. doi: 10.1109/MSP.2009.000000 |
| [7] | Saad W, Han Zhu, Basar T, et al. Distributed coalition formation games for secure wireless transmission[J]. Mobile Networks & Applications, 2011, 16(2): 231–245. |


