针对当前业务量预测方法过于理想化、预测准确度不高等问题,根据现网业务量特征提出了一种基于乘积季节自回归求和移动平均(S-ARIMA)模型的业务量预测方法.依据现网业务量的特征,详细分析了基于S-ARIMA的业务量预测建模的数学过程,经过现网大量业务量数据验证,S-ARIMA模型相比其他模型方法在预测值和置信区间上均具有较好的结果,是一种合理有效的业务量预测方法.
During the study of the technologies of energy saving, how to ensure the changing trend of traffic accurately is a prerequisite of many energy-saving technology. Contraposing the current methods for traffic prediction being a bit idealistic and the low accuracy prediction, we propose a traffic prediction method based on the seasonal autoregressive integrated moving average(S-ARIMA) model in view of the traffic character in the network and implement it. According to the characteristics of the traffic character in the network, We analyze the mathematical process of the S-ARIMA mode detailedly. It is tested by a lot of traffic data in the wireless communication networks and the results indicate that for prediction values and confidence intervals S-ARIMA model performs better than other models. Therefore, this traffic prediction for wireless communication networks using S-ARIMA model is reasonable and efficient.
随着通信网络规模和应用的迅猛扩张,使得节能减排问题成为ICT行业专注的核心问题之一[1].由于各网络节能技术研究的前提是未来业务量的变化情况,从而使得针对业务量的预测问题成为了各网络节能技术研究的基础.因此,针对业务量的预测问题成为了节能方法研究中的重要环节与影响因素之一.
在业务量的预测方法中,主要有傅里叶级数模型、结构分量模型(如Holt-winter’s模型)以及时间序列模型如自回归求和移动平均ARIMA(autoregressive integrated moving average model)模型[2].
由于业务量数据具有很强的随机性特点,傅里叶级数模型在近年来逐渐被以Holt-winter’s模型为代表的结构分量模型所取代[3-8]. Holt-winter’s模型在业务量数值较小(5Erlang)以下时表现不佳[6].在已有研究中,ARIMA模型作为时间序列分析模型的一种,由于ARIMA模型本身的限制,并不适用于周期性的数据.乘积季节ARIMA模型(S-ARIMA,seasonal autoregressive integrated moving average model)作为ARIMA模型的延展,很好的解决了ARIMA模型不足的问题,是目前为止用于业务量预测的最理想模型之一.
采用S-ARIMA模型对小区密度的业务量数据预测问题进行建模,并根据模型进行未来24 h的业务量数据预测,同时对ARIMA模型、傅里叶级数模型、Holt-winter’s模型进行建模对比分析,发现S-ARIMA模型在预测精度、模型误差方面均具有较好的结果,是目前一种较好的业务量预测模型.
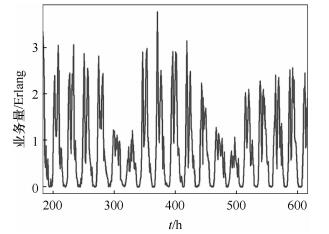
1 S-ARIMA模型 1.1 业务量的时间特征业务量数据在时间上存在着很大的波动性,在一段时间内业务量数据的大小是具有统计规律的.总的来说,由于业务量是和人的活动息息相关的,业务量存在着明显的周期性,因此适用于S-ARIMA模型.
|
图 1 业务量时间特征 |
S-ARIMA模型由基本的时间序列模型演变而来,在自回归求和移动平均模型的基础上考虑时间序列的季节性,将ARIMA模型扩展推广,用来描述具有季节性的时间序列问题.
S-ARIMA模型数学表达式如下:
| $ {\phi _p}\left( B \right){\Phi _P}({B^s}){\left( {1-B} \right)^d}{(1-{B^s})^D}{\dot Z_t} = {\theta _q}\left( B \right){\Theta _Q}({B^s}){a_t} $ | (1) |
为方便起见,通常分别称φp(B)和θq(B)为常规的自回归算子和移动平均算子(或多项式),分别称ΦP(Bs)和ΘQ(Bs)为季节性自回归算子和移动平均算子(或多项式).记B为后移算子(Bzt=zt-1),Zt为时间序列,at为零均值白噪声过程,p、P、q、Q为各算子阶数,d为差分阶数,D为季节性差分阶数,下标s为季节周期,当d=D=0时,S-ARIMA模型退化成ARMA模型.式(1) 中的模型一般记为ARIMA(p, d, q)×(P, D, Q)s,称为季节周期为s的ARIMA(p, d, q)×(P, D, Q)s模型.
1.3 模型识别的方法在建立S-ARIMA模型的过程中,基本的数学工具为相关性分析,即样本自相关函数(ACF,autocorrelation function)和样本偏自相关函数(PACF,partial autocorrelation function).
关于建立S-ARIMA模型的一般步骤,是以自相关函数作为先导的,具体步骤如下:
1) 对于给定的时间序列,做差分∇与季节差分∇ s,以得到平稳性序列;
2) 检查适当差分后序列的自相关函数,选择适当的p、d、q和P、D、Q值,选择一个尝试性的模型;
3) 通过差分序列的自相关值求得ARIMA(p, d, q)×(P, D, Q)s模型参数的初估计;
4) 经拟合后,对残差运用诊断检验过程,或者接受试验性模型,或者指出可以改进的方式,进而重新拟合并重复进行诊断检验.
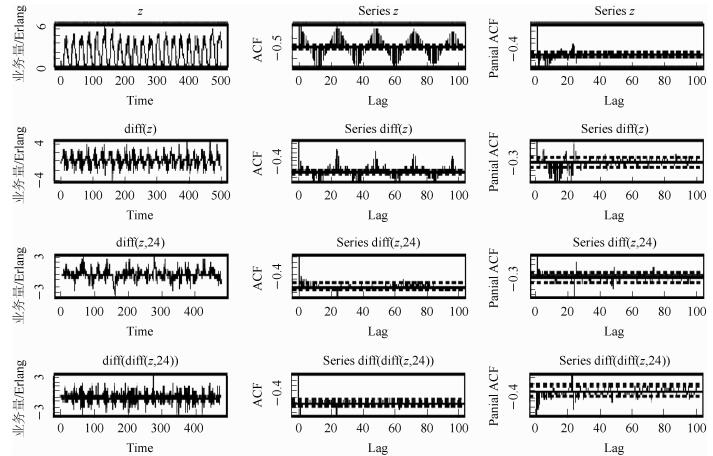
2 基于S-ARIMA模型的建模过程如图 2所示为对一个小区业务量数据通过多次差分进行的模型阶数识别的研究过程.
|
图 2 阶数识别过程 |
通过业务量原始数据可以看出业务量数据是非平稳的.业务量数据的ACF图显示,业务量数据具有明显的以24为周期的周期性.对业务量进行一阶差分进行平稳化处理后,仍可以从ACF图中看出周期性,同时可以看出,一阶ACF是截尾的,PACF是拖尾的.通过对业务量进行以24为间隔的季节差分来消除序列的季节性,可以看出该季节差分较好的消除了序列的季节性,ACF图和PACF图均显示没有周期出现,但是该序列并不是平稳的序列,仍然需要进行差分从而得到平稳的序列.通过对业务量数据进行以24为间隔的季节差分后再进行一次差分,此时序列接近于平稳序列,其ACF图和PACF图为1阶迅速衰减的阻尼震荡,由此可以进行预估计,将模型识别为S-ARIMA(1, 1, 1)×(0, 1, 1)24模型.其方程可表示为
| $ \begin{array}{l} (1-{\varphi _1}B)\left( {1-B} \right)(1-{B^{24}}){Z_t} = \\ (1 - {\theta _1}B)(1 - {\Theta _1}{B^{24}}){a_t} \end{array} $ | (2) |
其中:B为后移算子,at为白噪声.
将方程展开则方程可写为
| $ \begin{array}{l} {Z_t}-{Z_{t-1}}-{Z_{t - 24}} + {Z_{t - 25}} - \\ {\varphi _1}({Z_{t - 1}} - {Z_{t - 2}} - {Z_{t - 25}} + {Z_{t - 26}}) = \\ {a_t} - {\theta _1}{a_{t - 1}} - {\Theta _1}{a_{t - 24}} + {\theta _1}{\Theta _1}{a_{t - 25}} \end{array} $ | (3) |
随后通过最大似然法对模型进行参数估计,并进行假设检验.其参数为ϕ1=0.3231,θ1=-0.9474,Θ1=-0.928 6.
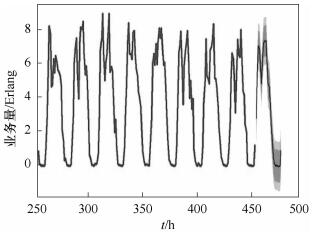
根据该模型进行业务量预测,得到24 h预测结果, 如图 3所示.
|
图 3 24 h预测结果 |
使用ARIMA模型、傅里叶级数模型以及Holt-winter’s模型作为对比模型与S-ARIMA模型进行对比.
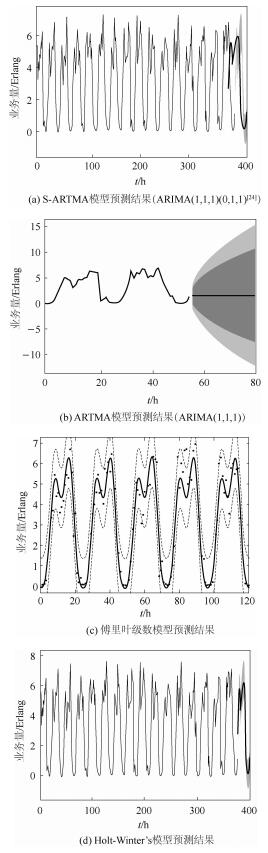
3.1 某基站小区的各模型预测结果比较首先,分别使用S-ARIMA模型、ARIMA模型、傅里叶级数模型(本文中适用预测效果最好的5阶傅里叶级数模型)以及Holt-winter’s模型对同一小区的业务量数据进行建模,并根据模型进行预测,分析预测数据的均方根误差(RMSE, root mean-square error)以及置信区间的大小.该小区的业务量数据为连续的400 h的数据, 其结果见图 4.
|
图 4 模型建模预测结果 |
ARIMA模型不适用于周期性数据,预测结果最差.傅里叶级数模型由于模型本身对随机性的适应性较差,且业务量的随机性特点比较显著,因此该模型的精确度较差. Holt-winter’s模型其预测结果与S-ARIMA模型结果相似.
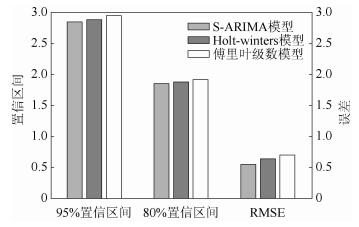
将S-ARIMA模型、Holt-winter’s模型以及5阶傅里叶级数模型的误差以及95%置信区间、80%置信区间进行对比,由图 5可以看出,傅里叶级数模型在95%置信区间以及RMSE数值上表现最差,即傅里叶级数模型精准度较差,与另外两种模型有明显差距. S-ARIMA模型误差最小,Holt-winter’s模型与S-ARIMA模型结果相似.
|
图 5 3种模型在某小区的预测结果对比 |
以上是对单个小区的业务量进行预测后的结果.通过对多个小区的业务量进行预测,依然可以得到S-ARIMA模型和Holt-winter’s模型预测结果相对较好的结论.在这里进一步研究S-ARIMA模型与Holt-winter’s模型的优劣性.根据53个宏站小区的业务量数据进行建模,并根据得到的模型进行业务量预测,将得到的预测结果与实际值进行比较.额外选取4个统计量作为比较标准,分别为平均绝对误差(MAD,mean absolute difference)、平均绝对相对误差(MARE,mean absolute relative error)、均等系数(EC,equal coefficient)以及置信区间.
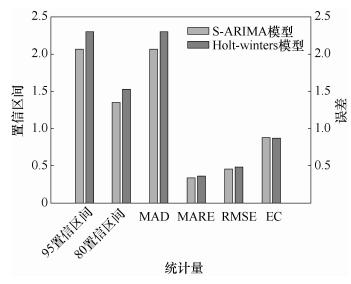
图 6为53个宏站小区的MAD、MARE、RMES、EC值以及80%置信区间、95%置信区间的平均值的对比示意图.从图 6中可以看出,在衡量预测值与实际值方面的EC值S-ARIMA模型达到88.2%,优于Holt-winter’s模型的87.4%.而MAD、MARE与RMSE等统计值也是S-ARIMA模型小于Holt-winter’s模型,即S-ARIMA模型的误差更小.
|
图 6 S-ARIMA模型与Holt-winter’s模型对比 |
同时,对于置信区间,S-ARIMA模型无论是80%置信区间,还是95%置信区间,其大小均小于Holt-winter’s模型相对应的置信区间的大小.因此,在模型精准度方面,S-ARIMA是优于Holt-winter’s算法的,而这一结论在EC值等统计量中也可以得到体现.
由此可以得出如下结论:S-ARIMA模型相比于Holt-winter’s模型而言,在预测值精准度上具有一定的优势,其误差更小,与实际数据吻合度更高.
4 结束语经研究通过现网业务量数据使用S-ARIMA进行数学建模,建立了S-ARIMA(1, 1, 1)×(0, 1, 1)24模型,并进行未来24 h业务量预测.同时将ARIMA模型、傅里叶级数模型、Holt-winter’s模型与S-ARIMA模型进行对比,并重点研究了Holt-winter’s模型与S-ARIMA模型的优劣性.结果显示S-ARIMA模型结果更加的精准,在4种模型中表现最好. S-ARIMA模型不仅在预测值的准确性上优于其他3种模型,而且在反映模型精确度的置信区间上要好于其他3种模型.但是在得到精准结果的同时,S-ARIMA模型也存在着复杂程度、计算开销大于傅里叶级数模型、Holt-winter’s模型的问题,而且在面对如室分站,即业务量较低的小区、随机性过大的小区时,S-ARIMA模型的准确度也会受到影响.同时,这仅仅是对于无线通信网业务量中的语音话务量的预测研究工作,对于更加复杂,随机性更强的数据业务量,将是接下来研究的重点.
| [1] | 喻鹏. 无线通信网的节能管理机制[D]. 北京: 北京邮电大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10013-1013326332.htm |
| [2] | 郭秉义. 绿色通信网络的节能方法研究[D]. 广州: 华南理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10561-1014063032.htm |
| [3] | Morosi S, Del Re E, Piunti P. Traffic based energy saving strategies for green cellular networks[C]//European Wireless, 2012. 18th European Wireless Conference. Poland:[s.n.], 2012:1-6. |
| [4] | Tikunov D, Nishimura T. Traffic prediction for mobile network using Holt-Winter's exponential smoothing[C]//International Conference on Software, IEEE, Paris:[s.n.], 2007:1-5. |
| [5] | Morosi S, Piunti P, Re E D. Sleep mode management in cellular networks: a traffic based technique enabling energy saving[J]. Transactions on Emerging Telecommunications Technologies, 2013, 24(3): 331–341. doi: 10.1002/ett.v24.3 |
| [6] | Paul U, Subramanian A P, Buddhikot M M, et al. Understanding traffic dynamics in cellular data networks[J]. Proceedings of IEEE INFOCOM, 2011, 8(1): 882–890. |
| [7] | Wyglinski A M, Labeau F, Kabal P. An efficient bit allocation algorithm for multicarrier modulation[C]//WCNC 2004 IEEE. Atlanta:[s.n.], 2004: 1194-1199. |
| [8] | Niu Z, Wu Y, Gong J, et al. Cell zooming for cost-efficient green cellular networks[J]. IEEE Communications Magazine, 2010, 48(11): 74–79. doi: 10.1109/MCOM.2010.5621970 |


