2. 解放军理工大学 指挥信息系统学院, 南京 210007
为了提高蜂窝式卫星移动通信的通信质量和频谱使用效率,必须对各波束载波频率的选取进行合理规划.为此,将频谱资源动态规划问题形式化,提出一种基于遗传算法和启发式搜索的频谱动态规划算法,综合考虑同频复用距离、波束分组类约束、动态变化的可用频谱资源、用户业务频谱需求等,动态地将可用频谱资源分配至各波束,以最大效用地利用卫星频谱资源.
2. College of Command Information Systems, PLA University of Science and Technology, Nanjing 210007, China
Appropriate carrier frequency allocating for satellite spot beams is necessary for improving the qaulity of service (QoS) and spectrum utilization efficiency of cellular satellite mobile communication systems. This paper formalizes the problem of dynamic carrier frequency allocating and then proposes a dynamic spectrum planning algorithm based on genetic algorithm(GA) and Heuristic Search, which comprehensively considers the frequency reuse distance, beam group constraint, varying spectrum resource available, and spectrum requirement of a spot beam, to utilize the spectrum resource as efficient as possible.
蜂窝式卫星移动通信系统中采用了大量的窄点波束,波束内的卫星通信采用众多窄带载波,这些窄带载波根据通信需求进行分配[1].为了提高蜂窝式卫星移动通信的通信质量和频谱使用效率,必须对各波束的载波频率选取进行合理的规划,使得相邻波束不使用同频载波,存在同频复用的波束之间的地域距离越大越好.另一方面,希望尽可能多地保留一些现有信道.传统方法将该问题转化为“最小集合”问题[2],当只考虑同频干扰时,变成“NP类完备”的图着色问题. “最小集合”问题只是简单地计算所需要的总频点数,不能最大效用地利用频谱资源.
首先将频谱资源动态规划问题形式化,综合考虑同频复用距离、波束分组类约束、动态变化的可用频谱资源、用户业务频谱需求等,提出一种基于遗传算法[3]和启发式搜索[4]的频谱动态规划算法,动态地将可用频谱资源分配至各个波束,以最大效用地利用卫星频谱资源.
1 卫星频谱规划问题描述 1.1 卫星频谱规划中的约束蜂窝式卫星移动通信的关键是频率复用,但为了获得一个允许的同频干扰,系统设计者必须保证同频波束之间的最小间距.另外,同频干扰还取决于同频波束数和每个转发器中的波束数.
在进行信道分配时必须受到以下干扰条件限制.
1) 同波束内约束:同一个波束内的所有信道不能重复.
2) 同信道约束:同一个信道不能在其同频干扰范围内再次使用.
3) 同组波束约束:考虑到某些波束对星上放大器等某些资源的共享特性,这些同一分组的多个波束也不能分配相同的信道.
1.2 问题的形式化描述首先将M可用信道用1、2、3、…、M等正整数依次标号.假设一个N个波束组成的卫星转发器,考虑前面提到的约束,可以定义一个N×N维对称矩阵D,称之为距离矩阵.定义C为干扰矩阵,其中的非对角元素cij表示分配给第i波束和第j个波束中的信道之间的最小间隔,而C中的对角线元素为给第i波束内一组信道之间的最小频点间隔.
定义1 波束距离为波束中心点之间的几何距离.两个相邻波束间的距离记为1,任意二个波束之间的实际几何距离与相邻波束间距离的比值,记为波束i与波束j间的距离dij.
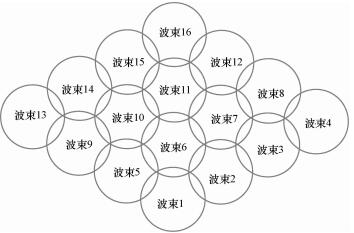
以图 1为例,波束1与波束2的距离为1,波束1与波束3的距离为2,波束1与波束10的距离为1.732(取小数点3位).
|
图 1 卫星波束示意图 |
如果波束i与波束j属于共用同一个转发器功放的一组波束,同一功放的各波束中频点不能重复,因此置dij=0.
定义2 fik表示分配给波束i使用的频点k,fjk表示分配给波束j使用的同一频点k,那么dijk为频点k关于波束i与波束j的复用距离.
定义3 分布在不同波束中的频点fik, i∈{1, 2, …, N},其最小复用距离记为
定义4 通过对系统中每个波束的话务量等分析,可以定义一个矢量Q={q1, q2, …, qi, …, qn}来表示每个波束的信道(频点)需求(称为需求矢量),qi表示第i个波束需要的信道数目.
根据以上定义,前面所述的分配约束,即一个波束中的频点不能重复,距离为1的两个波束中的频点不能重复,同一功放的不同波束中的频点不能重复,均可表示为
| $ d_{_{ij}}^{^k} > {\rm{Para}}, \;\;\forall i, j \in \left\{ {1, 2 \cdots, N} \right\}, \;\;\;\forall k \in \left\{ {1, 2, \cdots, M} \right\} $ | (1) |
其中Para>1为设定的最小同频干扰距离.
频谱资源需求可以表示为
| $ {\rm{card}}\left( { \cup \{ {f_{ik}}, k = 1, 2, \cdots, M\} } \right) \ge {q_i}, \;\;\forall i \in \left\{ {1, 2, \cdots, N} \right\} $ | (2) |
优化目标可以表示如下:
1) 优化目标1
| $ \hat M = {\rm{mincard}}\left( { \cup \{ k|{f_{ik}}, i \in 1, 2, \cdots, N\} } \right) $ | (3) |
即系统所需要用到的频点数目尽量少.
2) 优化目标2
| $ \hat L = \max \;\mathop {\min }\limits_{k \in \{ 1, 2, \cdots, M\} } \left( {\mathop {\min }\limits_{i, j \in \{ 1, 2 \cdots, N\} } d_{ij}^k} \right) $ | (4) |
即最大化最小重频距离,或者大于2、3、4等指定值.
2 基于遗传算法(GA)与启发式搜索的卫星频谱规划算法 2.1 基于遗传算法(GA,genetic algorithm)的频谱初始化分配波束的频谱资源分配问题可以作为一类组合优化问题进行求解.组合优化问题往往是不可微、不连续、高度非线性的“NP类完备”问题,通常带有大量的局部极值点,很难精确求出组合优化问题的全局最优解.遗传算法在解决诸多典型组合优化问题上显示了良好的性能和效果,因此采用GA对频谱资源进行初始分配.
1) GA的基本原理
GA是一类模拟生物界自然选择和自然遗传机制的随机化搜索算法,作为一种全局优化搜索算法,具有简单通用、鲁棒性强、适于并行处理以及应用范围广等显著特点[5].
遗传算法主要是引用了自然界进化中“优胜劣汰”的思想,群体中对环境适应强的优良个体比差的个体有更多机会相互进行杂交,继承各自好的特性,产生适应性更强的后代.遗传算法中包含了如下5个基本要素:① 参数编码;② 初始群体的设定;③ 适应度函数的设计;④ 遗传算子设计;⑤ 控制参数设定(主要是指群体大小和使用遗传算子的概率等).
2) 适应度函数
GA在进化搜索中的目标函数即适应度函数,适应度函数评估是选择操作的依据,其设计将直接影响到GA的性能.适应度函数为
| $ \hat L = \max \;\mathop {\min }\limits_{k \in \{ 1, 2, \cdots, M\} } \left( {\mathop {\min }\limits_{i, j \in \{ 1, 2 \cdots, N\} } d_{ij}^k} \right) $ |
3) 遗传算子
在GA中有选择、交叉和变异3个主要算子.选择算子的目的是为了从当前群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙.判断个体优良与否的标准是各自的适应度值.
4) 对问题求解
问题目标是求出n个波束和m个频点的初始最优分配,定义分配矩阵S,其中sij, i=1, 2…, n, j=1, 2, …, m. sij代表第i个波束中布置了第j个频点布置情况.其中sij为0代表没有布置;sij为1代表在第i个波束中布置了第j个频点. S中的每一列(共m列)代表每一个频点在所有波束中的布置.
将S矩阵按列抽取出来,形成{s1, s2, …, si, …, sm},构建种群结构s′=[s′1, s′2, …, s′i, …, s′m].
根据分配约束,通过变异、交叉过后的种群个体,应满足式(1) 的要求,不满足要求的个体首先予以剔除.筛选个体的适应度函数为
| $ \hat L = \max \;\mathop {\min }\limits_{k \in \{ 1, 2, \cdots, M\} } \left( {\mathop {\min }\limits_{i, j \in \{ 1, 2 \cdots, N\} } d_{ij}^k} \right) $ |
算法迭代终止的条件是:如式(2) 所示,满足每个波束的频谱需求,且适应度函数值增量/迭代轮数 < 设定阈值.
2.2 频谱资源动态规划算法动态频谱资源分配策略中所有波束都没有固定分配的频谱,所有频率资源都能在任意波束内使用.这种分配可以根据业务需求、环境因素等动态调整,只要满足相应的频率复用限制即可.
频谱资源动态规划算法将系统可用频谱资源和各个波束的频谱需求作为问题变量,以系统各项约束作为问题约束条件,求解系统资源使用最小化、系统容量最大化的目标问题.算法总体思路采用启发式搜索[4],搜索过程中考虑如下启发原则:
1) 每轮优先分配频谱需求高的波束;
2) 每轮分配中,以等于最小复用距离为一簇,逐簇进行分配,尽量避免过远距离,以免影响系统总体容量;
3) 综合根据频率复用成本函数和频率间隔成本函数,为某波束挑选频率资源.
频谱资源动态规划算法流程如下:
1) 根据初始频谱分配方案和需求变化,选择频谱需求最高波束,入候选表,清空禁忌表;
2) 从候选表中选择某频谱需求最高波束,对该波束及其干扰波束、频谱需求未满足的,分别在其满足复用距离约束的可用频谱中,根据频率复用成本函数和频率间隔成本函数,挑选1个或1组信道分配给对应波束;
3) 对该波束及其干扰波束入禁忌表;
4) 该波束出候选表,对该波束等复用距离的波束,未在禁忌表的入候选表;
5) 若候选表为空或禁忌表满,转6);否则转2);
6) 若本轮未新分配频率资源或所有波束满足频谱需求,结束;否则转1).
在动态频谱资源分配策略中,根据所采用的成本函数算法计算每个频点在每个波束中使用时的成本,算法选择成本最低的频点进行分配.不同的成本函数算法决定了不同的动态分配策略.下面给出一种计算频点i在波束x中分配成本函数Cx(i)的算法, 定义如下.
I(x):到波束x的距离小于同频复用距离D的所有波束(即波束x的干扰波束)的集合;
Λ(x):波束x当前时刻的可用频点的集合;
FD(k):根据完全固定分配算法预先固定分配给波束k使用的频点集合,或者说是波束k的最优标称信道集.
此算法的成本函数可用下式计算:
| $ {C_x}\left( i \right) = \sum\limits_{k \in I\left( x \right)}^{} {\left\{ {{u_k}\left( i \right)} \right\}}, \;\;\;\forall i \in \mathit{\Lambda} \left( x \right) $ | (5) |
其中
| $ {u_k}\left( i \right) = \left\{ \begin{array}{l} 1, \;\; 如果 i \in \mathit{\Lambda} \left( k \right)\\ 0, \;\; 其他 \end{array} \right. $ |
一旦确定频点i在波束x中使用成本函数Cx(i),对于某一时刻波束x的频谱需求,只要满足
| $ {C_X}\left( {{i^*}} \right) = {\rm{mi}}{{\rm{n}}_{i \in \mathit{\Lambda} \left( x \right)}}\left\{ {{C_X}\left( i \right)} \right\} $ | (6) |
频点i*就被分配给波束x.
当波束x频谱资源需求降低时,可以重新安排频谱分配计划,即从波束x中释放一些正被其他波束使用的成本最高的频点.
对分配在波束x中每个频点j计算其去分配成本函数Rx(j),如果满足下列条件,波束x中的频点j′就被释放:
| $ {R_x}\left( {j\prime } \right) = {\rm{mi}}{{\rm{n}}_{j \in A\left( x \right)}}\left\{ {{R_x}\left( j \right)} \right\} $ | (7) |
其中A(x)是波束x中正在使用的频点集合.
计算波束x中频点j去分配函数Rx(j)的公式为
| $ {R_x}\left( j \right) = 1-{q_x}\left( j \right) + \sum\limits_{k \in I\left( x \right)}^{} {\left\{ {{R_x}\left( {k, j} \right)} \right\}}, \;\;\forall j \in A\left( x \right) $ | (8) |
其中:Rx(k, j)=bx(k, j)+2qk(j),∀k∈I(x).
| $ \begin{array}{l} {b_x}\left( {k, j} \right) = \left\{ \begin{array}{l} 0, \;\;\; 如果信道j在波束k中不可分配, 只被分配在波束x中\\ 1, \;\;\;其他 \end{array} \right.\\ {q_k}\left( i \right) = \left\{ \begin{array}{l} 0, \;\;如果i \in {F_D}K\left( k \right)\\ 1, \;\;其他 \end{array} \right. \end{array} $ |
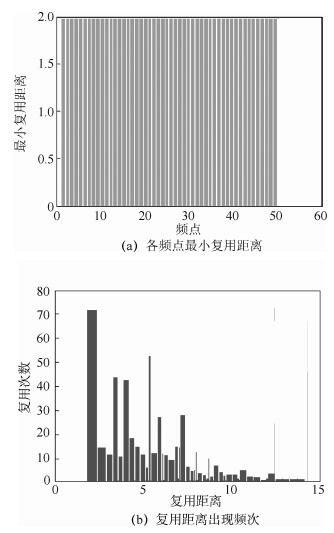
在给定某波束覆盖的情况下,输入可用频点数目、最小复用距离约束、波束组约束、各波束的频谱需求,采用本文中的动态频谱规划算法,可以一次性生成优化的频谱分配方案;在给定初始分配方案基础上,频谱需求等发生变化时,可以增量地动态生成修改后的分配方案.对生成的频谱规划方案,可以统计各个频点的复用距离、不同复用距离的频次、系统的最大容量等各类评估参数.
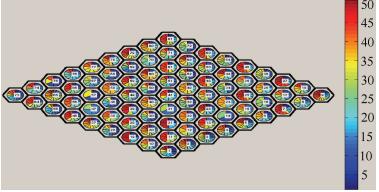
设64个波束呈菱形分布,可用频点数目为50,最小同频复用距离为2,各个波束的频点需求为5~15不等,波束按编号分为4组,频谱规划结果如图 4所示.规划方案的统计评估结果如图 5所示,总可用频点50个,已使用频点50个,保留频点0个.系统总分配频点(次):836.总体最小复用距离:2000.
|
图 4 多波束频谱规划结果 |
|
图 5 卫星频谱规划方案评估 |
其他条件相同,在不同的最小同频距离约束条件下,对应的频谱规划方案的系统总容量如表 1所示.
|
|
表 1 同频约束距离与系统容量的关系 |
提出一种基于遗传算法和启发式搜索的蜂窝式卫星移动通信频谱动态规划算法,综合考虑同频复用距离、波束分组类约束、动态变化的可用频谱资源、用户业务频谱需求等,动态地将可用频谱资源分配至各波束,可以有效地提高卫星频谱资源的利用率.
| [1] | 胡圆圆. 多波束卫星通信系统资源的动态分配研究[D]. 南昌: 南昌航空大学, 2014. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hbyd201505153&dbname=CJFD&dbcode=CJFQ |
| [2] |
张馨, 薛质, 范磊. 基于最小集合覆盖的网络连通性自动化测试[J]. 计算机工程, 2012, 38(24): 65–69.
Zhang Xin, Xue Zhi, Fan Lei. Network connectivity automatic test based on minimum set cover[J]. Computer Engineering, 2012, 38(24): 65–69. |
| [3] |
庄健, 杨清宇, 杜海峰, 等. 一种高效的复杂系统遗传算法[J]. 软件学报, 2010, 21(11): 2790–2801.
Zhuang Jian, Yang Qingyu, Du Haifeng, et al. High efficient complex system genetic algorithm[J]. Journal of Software, 2010, 21(11): 2790–2801. |
| [4] |
徐艳艳, 岳伟亚. 基于BDD的增量启发式搜索[J]. 软件学报, 2009, 20(9): 2352–2365.
Xu Yanyan, Yue Weiya. BDD-based incremental heuristic search[J]. Journal of Software, 2009, 20(9): 2352–2365. |
| [5] | Goldberg D E, Holland J H. Genetic algorithms and machine learning[J]. Machine Learning, 1988, 3(2): 95–99. |


