2. 中国人寿电子商务有限公司, 北京 100033
突发公共事件发生后,应急资源调度作为应急管理的重要环节,是其实现救援价值的重要体现.首先从应急管理角度分析了资源调度策略的影响因素,然后以优化时间满意度、成本耗费和需求满意度为目标构建多目标应急资源调度模型,通过引入粒子群算法求解多目标函数,决策出效用满意度最大的资源调度方案.最后,以效用满意度作为应急资源调度的均衡性指标.仿真实验结果表明,该方法具有较好的效用满意度,提高了资源调度的有效性.
2. China Life Ecommerce Company Limited, Beijing 100876, China
After the occurrence of public emergency, resource scheduling is an important part of emergency management which is the realization of the rescue value. Firstly, the influencing factors of resource scheduling policy is analyzed from the perspective of emergency management. Secondly, the emergency resource scheduling model is established to optimize the time satisfaction, expenses cost and the demand satisfaction. Besides, this paper solves multi-objective resource scheduling using the particle swarm algorithm and chooses the resource scheduling scheme of the greatest utility satisfaction. Finally, utility satisfaction is used as the balance index of emergency resource scheduling. The simulation results show that this method has better utility satisfaction and improves the effectiveness of resource scheduling greatly.
突发公共事件发生初期,应急资源严重短缺,由于各种不确定性因素,资源需求量难以预测,加大了资源调度问题的复杂性[1].现阶段关于应急资源调度模型的研究中,对应急资源调度的目标集中于降低总的应急时间和成本,未将应急资源调度的有效性和满意度量化为相应评价指标来参与模型构建.提出以应急救援效用满意度作为应急资源调度的均衡性指标,从优化应急资源配送时间、配送成本大小和资源有效性3个方面构建多目标资源调度模型,解决在应急资源种类和数量一定的前提下尽可能缩小各受灾点满意率差异的问题.
1 多目标应急资源调度模型 1.1 资源调度策略影响因素突发公共事件按照其性质、严重程度、可控性和影响范围等因素,可分为四级:Ⅰ级(特别重大)、Ⅱ级(重大)、Ⅲ级(较大)和Ⅳ级(一般)[2].突发公共事件的分级决策结果决定了受灾点的应急资源利用率.除此之外,资源需求量、出救点到灾害点的距离、车辆调度的耗费也是资源调度策略的影响因素.
采用文献[3]中的预警分级综合模糊评判模型,该模型输出一个预警分级综合决策结果B,B根据最大隶属度原则,综合评判得出最终的预警等级,将最终的预警等级系数分别用γ来量化表示.
1.2 问题描述以优化资源调度的效用满意度和资源调度成本为目标,建立相应资源调度模型,求解资源调度方案[4].已知出救点集合R=[1, 2, …, m]到受灾点集合T=[1, 2, …, n]中各个点的距离,同时给出资源种类集合U=[1, 2, …, h]和各受灾点的资源需求数量,以优化配送时间、配送成本和资源有效性为目标,确定资源供应点集合R到受灾点集合T的多目标资源调度方案P.
1.3 模型建立应急资源调度方案由配送时间、配送成本和资源有效性影响.应急资源连续均匀的耗费的情况下,资源配送时间由运输的路径长度决定,φrt表示在资源调度方案P下出救点r到受灾点t的可能性,drt表示供应点r到受灾点t的距离,v为车辆的速度[4].应急资源调度的时间耗费函数为
| $ {f_1}\left( x \right) = \sum\limits_{r = 1}^m {\sum\limits_{t = 1}^n {\frac{{\varphi _{_r}^{^t}d_{_r}^{^t}}}{v}} } $ | (1) |
资源配送成本由调度的车辆数决定,调度数量由调度到该灾害点的总资源数量决定,Crt表示出救点r到受灾点t的车辆调度数量,应急资源调度的成本耗费函数为
| $ {f_2}\left( x \right) = \sum\limits_{r = 1}^m {\sum\limits_{t = 1}^n {\varphi _{_r}^{^t}c_{_r}^{^t}} } $ | (2) |
应急资源调度的有效性由受灾点的预警等级、资源的需求量和资源调度量共同决定.资源种类集合为U=[1, 2, …, h],其中h种资源的重要程度比为σ1:σ2:…:σh,用Xrut表示P下资源供应点到受灾点t调度种类为u的资源数量,nut表示受灾点t对u类资源的需求量,Kt为灾害点t的预警等级系数,Ⅰ级、Ⅱ级、Ⅲ级和Ⅳ级对应的γ值分别为4、3、2、1.应急资源调度的需求满意率函数为
| $ {f_3}\left( x \right) = \frac{{\sum\limits_{r = 1}^m {\sum\limits_{t = 1}^m {\sum\limits_{u = 1}^h {{\gamma ^t}\varphi _{_r}^{^t}{\sigma _u}x_{_{ru}}^{^t}} } } }}{{\sum\limits_{t = 1}^n {} \sum\limits_{u = 1}^h {{\gamma ^t}{\sigma _u}n_{_u}^{^t}} }} $ | (3) |
总目标函数为
| $ F\left( x \right) = {\rm{min}}({\tau _1}{f_1}\left( x \right) + {\tau _2}{f_2}\left( x \right) + {\tau _3}{f_3}\left( x \right)) $ | (4) |
约束条件:
| $ \varphi _{_r}^{^t} = \left\{ \begin{array}{l} 0, \sum\limits_{u = 1}^h {x_{_{ru}}^{^t} = 0} \\ 1, \sum\limits_{u = 1}^h {x_{_{ru}}^{^t} > 0} \end{array} \right. $ | (5a) |
| $ \forall t \in T, \sum\limits_{r = 1}^n {\varphi _{_r}^{^t} \le m} $ | (5b) |
| $ \sum\limits_{r = 1}^m {} \sum\limits_{t = 1}^n {\varphi _{_r}^{^t} \le mn} $ | (5c) |
| $ 0 \le \varphi _{_r}^{^t} \le 1 $ | (5d) |
| $ \delta c_{_r}^{^t} = \sum\limits_{u = 1}^h {x_{_{ru}}^{^t}} $ | (5e) |
| $ {\tau _1} + {\tau _2} + {\tau _3} = 1 $ | (5f) |
采用线性加权法对目标函数加权,τ1、τ2、τ3分别为配送时间、配送成本和资源有效性的加权系数.约束条件(5a)是对资源调度方案的0~1约束;约束条件(5b)是对于每个灾害点,出救点的个数不超过总个数;约束条件(5c)保证出救点到灾害点资源调度映射关系数量限制;约束条件(5d)是调度方案P下从出救点r到受灾点t的可能性约束; 约束条件(5e)是配送资源车辆数与调度资源数量的系数关系.总目标函数的Pareto最优解即为应急资源调度方案[5].
2 粒子群算法求解目标函数采用粒子群优化(PSO, particle swarm optimization)算法求解多目标应急资源调度问题,在决策变量空间初始化一个粒子群,粒子迭代优化,最后粒子落入非劣最优目标域,得到多目标函数的Pareto最优解. PSO算法更新公式为
| $ {v_{i + 1}} = \omega {v_i} + {\alpha _1}{\theta _1}\left( {{x_{pb}}-{x_i}} \right) + {\alpha _2}{\theta _2}\left( {{x_{gb}}-{x_i}} \right) $ | (6) |
| $ {x_{i + 1}} = {x_i} + {v_{i + 1}} $ | (7) |
其中:xpb表示粒子本身达到过的最优位置,xgb表示整个粒子群到达过的最优位置,xi表示第i个粒子当前的位置,vi表示其当前速度;ω表示粒子的惯性权重,α1、α2表示粒子的加速度,其中α1表示粒子向本身最优位置移动的趋势,α2表示粒子向全局最优位置移动的趋势,θ1、θ2是(0, 1) 之间均匀产生的随机数.
对传统的PSO算法进行了改进,重新定义粒子的位置与速度,根据粒子在迭代过程中适应度值F(x)的变化,动态调整粒子速度更新的权重,提高了粒子群算法的收敛速度.粒子重定义为Xit=[x1t, x2t, …, xmt],其中t表示受灾点编号,t∈{1, 2, …, n},Xmt表示出救点m调度至受灾点t的资源数量.将粒子的速度定义为Vit=[v1t, v2t, …, vmt],速度表示从资源供应点j到受灾点i调度u类资源的变化量,通过迭代,改进算法得到资源调度的最佳方案.针对PSO算法容易陷入局部搜索的现象,动态调整不同迭代阶段惯性权重ω的取值,使算法能够自适应地调整全局系数.对PSO算法做出如下改进:
| $ \begin{array}{l} \omega \left( {k + 1} \right) = \omega \left( k \right)-k\left( {{\omega _{{\rm{max}}}}-{\omega _{{\rm{min}}}}} \right)/K\\ {\omega _{{\rm{max}}}} = 0.9, {\omega _{{\rm{min}}}} = 0.4 \end{array} $ | (8) |
算法通过自适应惯性权重动态调整后的形式为
| $ v_{_i}^{^{k + 1}} = \omega (k)v_{_i}^{^k} + {\alpha _1}{\theta _1}\left( {{x_{\rm{pb}}}\left( k \right)-x_{_i}^{^k}} \right) + {\alpha _2}{\theta _2}\left( {{x_{\rm{gb}}}-x_{_i}^{^k}} \right) $ | (9) |
基于粒子群算法的多目标资源调度函数求解算法的具体步骤如下.
输入:受灾点个数n,出救点个数m,算法最大迭代次数K
输出:适应度值F(xgb)和资源调度方案xgbt
第1步 随机生成初始位置xi和初始速度vi,计算出粒子适应度F(xi);
第2步 将F(xi)排序得到全局最优初始位置xgb,设定粒子个体的最优初始位置为xpb;
第3步 如果k==K,则转至步骤5;
第4步 1) 对每个可行的粒子xi,计算其F(xi),如果F(xi)≤F(xpb),则xpb=xi,如果F(xpb)≤F(xgb),则xgb=xpb;2) 根据迭代函数完成速度和位置更新;3) 转至第3步;
第5步 输出结果,结束.
3 仿真采用经济学中的效用理论,建立应急救援中资源调度效用函数,优化资源调度方案[6].在应急救援领域,效用满意度由时间满意度和需求满意度决定.将应急资源调度的效用满意度作为调度方案的评价指标,建立受灾点i的应急满意率的效用函数为[7]
| $ \begin{array}{l} {S_i}\left( {{t_i}, {\rho _i}} \right) = S_{_i}^{^0}-t_{_i}^{^\alpha } + \rho _{_i}^{^\beta } = \\ S_{_i}^{^0}-{\left( {\sum\limits_{r = 1}^m {} \sum\limits_{t = 1}^n {\frac{{\varphi _{_r}^{^t}d_{_r}^{^t}}}{v}} } \right)^\alpha } + {\left( {\sum\limits_{r = 1}^m {} \sum\limits_{t = 1}^m {} \sum\limits_{u = 1}^h {x_{_{ru}}^{^t}} {\sigma _u}} \right)^\beta } \end{array} $ |
其中:α和β表示资源u时间满意度和需求满意度的权重系数,α+β=1;Si0表示初始满意度,大小为第2部分PSO算法确定方案的初始满意度. h种资源的重要程度比为σ1:σ2:…:σh.参数取值如表 1所示.
|
|
表 1 实验中用到的参数值 |
采用所提算法作为应急救援决策模块的主体调度方案,Matlab随机生成出救点集合和受灾点集合以及各出救点到各受灾点的距离(见表 2),同时给出资源种类集合,如表 3所示.资源调度方案作为输出结果.
|
|
表 2 出救点到受灾点距离 |
|
|
表 3 受灾点资源需求的单位量 |
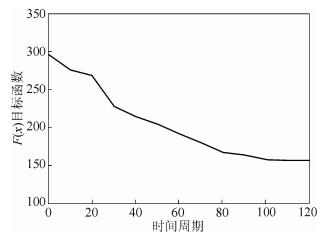
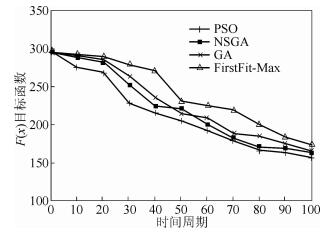
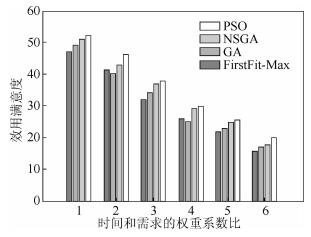
4个出救点的预警等级分别为Ⅳ、Ⅲ、Ⅰ、Ⅳ,对得到的结果进行分析. 图 1是PSO算法迭代次数对目标函数值的影响,当迭代次数达到100次时,PSO算法开始收敛,并趋向定值.将PSO算法、多目标遗传算法(NSGA)、遗传算法(GA)和优先满足预警等级最大原则(firstFit-max)生成的应急资源调度预案进行仿真比较,图 1实验结果表明PSO算法具有较快的收敛速度和更好的优化结果,图 3所示为各算法的效用满意度结果.
|
图 1 目标函数值随PSO迭代次数变化 |
|
图 2 各算法迭代优化求解目标函数值对比 |
|
图 3 效用满意度示意图 |
针对突发公共事件发生初期的多目标资源调度问题,提出以效用满意度作为应急资源调度的均衡性指标,通过构建多目标资源调度模型,得到多目标函数的Pareto最优解,决策出效用满意度最大的资源调度方案.仿真结果表明调度方案在时间、成本和需求满意率上都得到了优化,保证在有限的资源下最大化各灾害点的效用满意度,提高了整个救援流程的效率,有效实现了救援价值.
| [1] | Cheng Shuying, Yan Haifeng, Yin QiaoLin. The distribution path optimization problem of emergency logistics[C]//International Conference of Logistics Engineering and Management. 2012: 854-859. https://www.mendeley.com/research-papers/distribution-path-optimization-problem-emergency-logistics/ |
| [2] | 谢晓刚. 武警部队处置突发事件分级评价研究[D]. 长沙: 国防科学技术大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-90002-2009214173.htm |
| [3] |
季学伟, 翁文国, 倪顺江, 等. 突发公共事件预警分级模型[J]. 清华大学学报(自然科学版), 2008, 48(8): 1252–1255.
Ji Xuewei, Weng Wenguo, Ni Shunjiang, et al. Warning classification model for public emergencies[J]. Journal of Tsinghua University(Science and Technology), 2008, 48(8): 1252–1255. |
| [4] | Chang F S, Wu J S, Lee C L, et al. Greedy search based multi-objective genetic algorithm for emergency logistics scheduling[J]. Expert Systems with Applications, 2014, 41(6): 2947–2956. doi: 10.1016/j.eswa.2013.10.026 |
| [5] | Zhang Liming, Lin Yuhua, Yang Guofeng, et al. Lina emergency resources scheduling based on adaptively mutate genetic algorithm[J]. Computers in Human Behavior, 2001, 27(5): 1493–1498. |
| [6] |
宋亚楠, 仲茜, 刘斌. 基于边际效用函数的网络资源调度[J]. 电子学报, 2013, 41(4): 632–638.
Song Yanan, Zhong qian, Liu Bin. Marginal utility function based networking resource scheduling[J]. Acta Electronica Sinica, 2013, 41(4): 632–638. |
| [7] |
殷波, 王颖, 邱雪松, 等. 一种面向云服务提供商的资源分配机制[J]. 电子与信息学报, 2014(1): 15–21.
Yin Bo, Wang Ying, Qiu Xuesong, et al. A resource provisioning mechanism for service providers in cloud[J]. Journal of Electronics and Information Technology, 2014(1): 15–21. |


