2. 西安电子科技大学 通信工程学院, 西安 710071
针对混合供电的点到点无线通信链路,讨论了能量收集过程、数据到达过程以及衰落信道统计分布均未知情况下发射机的能量调度和自适应发送功率问题,目的是在保证通信系统一定性能的要求下最小化传统电网的能耗,即有效利用可再生能源的能量.基于Lyapunov优化提出一种低复杂度动态算法,理论证明了该算法可使优化目标无限趋于最优,同时保证最大数据时延不超过用户要求.仿真结果表明,提出的算法在性能和数据时延上都优于其他2种贪婪算法.
2. School of Telecommunications Engineering, Xidian University, Xi'an 710071, China
The problems of energy scheduling and adaptive transmission power were explored for a point to point wireless communication link, where, the transmitter is driven by hybrid energy sources. The problems are further constrained by the unknown information including 1) the energy harvesting process, 2) time-varying channel condition as well as 3) the statistics of dynamic/opportunistic data arrivals. To minimize the time average energy consumption from power grid over subject to a certain communication performance, i.e., utilizing efficiently the harvested energy, a new dynamic algorithm with low complexity was proposed based on Lyapunov optimization. Analysis shows that the proposed algorithm performs arbitrarily close to the optimal objective value, meanwhile ensures that the maximum time delay of the data queue would tolerate the data packets aggregated from the users' requirements. Simulations demonstrates that the proposed algorithm not only outperforms but also has smaller time delay than the other two greedy algorithms.
在能效和环境的驱动下,具有能量收集(EH, energy-harvesting)功能的无线通信网络可从周边可再生能源(太阳能、风能等)收集清洁能量自给自足从而节约传统能源而备受关注[1-2].但由于EH受到天气等因素的影响,从自然环境中收集的能量具有间歇性且能量大小具有随机性,如何有效地利用收集的能量成为当今的研究热点[3-4].
目前已有许多研究者致力于EH无线通信系统传输策略和能量管理的研究[5-7],它们共同的特点是针对流量低、EH作为唯一供电源的通信系统.由于EH过程的间歇性和随机性,文献[5-7]中所提的方案不适用于大功率通信网络,如蜂窝网.为保证大功率通信网络的可靠运行,可再生源和传统电网混合能源供电方案引起了工业界和科学工作者的极大兴趣.混合能源供电通信系统的大部分研究者[8-10]所提出的在线算法一般基于动态规划,要求给定能量收集过程等随机过程的统计知识.而在实际混合供电通信系统中,动态的移动数据流以及时变信道状态同EH过程一样,都具有随机性和不可预测性,很难获得这些随机过程的统计特性.因此这些算法[8-10]不适用于EH过程、信道状态以及数据到达过程统计特性未知的混合能源供电无线通信系统.
笔者研究EH过程、随机到达发射机的数据以及信道状态概率分布未知的情况下,点到点无线通信中混合供电发射机的能量调度和自适应发送功率问题,因此研究更具有一般性.笔者将该问题规划成随机网络优化问题,基于Lyapunov优化和排队论提出一种自适应功率算法和能量调度方案,在保证数据等待时延不超过给定要求的前提下,有效利用从可再生源中收集的能量,尽可能减小发射机在传统电网中的能耗,从而减少二氧化碳的排放量.本研究为混合供电发射机提供了一般情况下(未知随机过程统计信息)的能量调度和自适应功率算法,因此有利于绿色通信的设计.
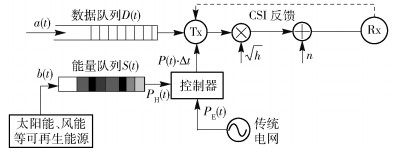
1 建模和问题描述混合供电发射机在点到点通信链路模型如图 1所示,发射机(Tx)由可再生能源和传统电网共同供电.发射机配备的各种EH器件从不同可再生源,如太阳能、风能等联合收集的能量缓存在能量队列(充电电池)中.由于发射机的主要能耗是发送数据所带来的能耗,简化起见,假设能量队列中缓存的能量只供发射机发送数据使用,系统其他能耗(如信号处理带来的能耗)由传统电网提供[11].假设发射机在离散时间t(t=0, 1, 2, …)上运行,时隙间隔固定为Δt.
|
图 1 混合供电发射机在点到点通信链路模型 |
假设t时隙随机到达的数据量用a(t)表示,数据进入数据队列D(t)排队等待传输,这里D(t)表示积压的数据量,且D(0)=0. t时隙离开数据队列的数据量记为μ(t)Δt,这里μ(t)是t时隙无线链路的传输速率, 即表示平均有多少比特的数据被传输(数据到达发射机可能以数据包的形式到达,这里假设数据包可以任意分割).则下一时隙数据队列的积压D(t+1)为(数据队列更新公式)
| $ D\left( {t + 1} \right) = \max \left[ {D\left( t \right) - \mu \left( t \right)\Delta t,0} \right] + a\left( t \right) $ | (1) |
μ(t)的大小取决于发射机的发送功率P(t)和时变信道当前的信道状态h(t),即链路增益.
高斯衰落信道的传输速率和发射功率之间的关系可用“速率-功率”公式表示[3]为
| $ \mu \left( t \right) = \frac{1}{2}{\rm{lb}}\left[ {1 + h\left( t \right)P\left( t \right)} \right] $ | (2) |
假设时变信道的信道状态h(t)∈H,∀t,H为有限集,每个时隙内信道状态h(t)保持不变,且有hmin≤h(t)≤hmax,这里hmin、hmax为常数.
由于数据源源不断地到达发射机等待传输,发射机应该尽可能地发送数据以避免数据积压越来越多;而为使发射机从传统电网的能耗最小,则应等待收集更多的能量,且选择信道状态较好的时隙发送数据.因此发射机决策t时隙的发送功率P(t)大小,取决于数据队列的当前积压、接收用户可忍受的时延、信道状态以及能量队列中的可用电量,即等待收集更多的能量或更好的链路状况,还是迫于队列积压过多造成数据等待时延太大而不得不从传统电网消耗能量.
这里0≤P(t)≤Pmax,Pmax为发射机的最大发送功率.发射机实际工作时会损耗一部分能量,用
| $ P\left( t \right) = {P_{\rm{H}}}\left( t \right) + {P_{\rm{E}}}\left( t \right) $ | (3) |
其中:PH(t)为从能量队列消耗的功率,PE(t)是从传统电网消耗的功率,PH(t)≥0且PE(t)≥0.
假设时隙到达能量队列的电量为b(t)个单位,当前存储的能量用B(t)表示,电池的特性不理想,每时隙的漏电量为ε(假设为常数),则能量队列B(t)更新如下:
| $ \begin{array}{*{20}{c}} {B\left( {t + 1} \right) = }\\ {\min \left( {\max \left[ {B\left( t \right) - \rho {P_{\rm{H}}}\left( t \right)\Delta t - \varepsilon ,0} \right] + b\left( t \right),{B_{\max }}} \right)} \end{array} $ | (4) |
其中Bmax为能量队列(电池)的最大容量,假设能量队列初值B(0)=0.由于能量队列容量有限并且漏电,所以应控制发射机优先使用能量队列里存储的能量,以便将来可容纳更多收集的能量,从而减小因电池容量有限造成能量溢出而产生的浪费,当能量队列中的可用能量不足于发射机综合各因素决策的功率消耗时,才从传统电网的消耗电量.
2 问题规划和求解目标是在EH过程、数据到达过程以及信道状态统计概率未知的情况下研究一种动态算法,通过自适应地调整发射机发送功率,并通过控制器对混合电源供电调度,在保证数据队列积有限且数据等待时延不超过用户要求的条件下,使发射机从传统电网消耗的平均电量最小.基于上述模型和目标,该问题可规划成随机网络优化问题,描述如下:
| $ \min :\mathop {\lim }\limits_{t \to \infty } \frac{1}{t}\sum\limits_{\tau = 0}^{t - 1} {E\left\{ {\rho {P_E}\left( \tau \right)\Delta t} \right\}} $ | (5) |
| $ {\rm{s}}.\;{\rm{t}}.\;:\overline {D\left( t \right)} < \infty $ | (6) |
| $ D\left( t \right)中所有数据等待小于{T_{\max }} $ | (7) |
| $ \mu \left( t \right) = \frac{1}{2}{\rm{l}}{{\rm{b}}_2}\left[ {1 + P\left( t \right)h\left( t \right)} \right],\forall t $ | (8) |
| $ P\left( t \right) = {P_H}\left( t \right) + {P_E}\left( t \right) $ | (9) |
| $ 0 \leqslant P\left( t \right) \leqslant {P_{\max }} $ | (10) |
| $ {P_H}\left( t \right) \geqslant 0,{P_E}\left( t \right) \geqslant 0 $ | (11) |
约束(6)是数据队列稳定的定义[12],其中
为实现约束(7), 需要构造一个虚拟队列来解决这一问题.让Z(t)表示虚拟队列,且有Z(0)=0,固定参数δ>0,虚拟队列根据以下公式更新:
| $ Z\left( {t + 1} \right) = \max \left[ {Z\left( t \right) + \delta \cdot {1_{\left\{ {D\left( t \right) > 0} \right\}}} - \mu \left( t \right),0} \right] $ | (12) |
其中1{D(t)>0}是一个指示变量,如果D(t)>0时,其值为1,否则为0.
如果通过控制发送功率P(t),使实队列D(t)和虚队列Z(t)稳定,即上确界有限,D(t)≤Dmax,Z(t)≤Zmax,则可以保证数据队列中所有数据等待的最大时间不超过Tmax个时隙[12].
| $ {T_{\max }} = \frac{{{D_{\max }} + {Z_{\max }}}}{\delta } $ | (13) |
调整参数δ可改变数据队列的最大等待时延Tmax,使其满足接收用户的时延要求.现在原问题(5)~(11)中约束(7)则转变为
| $ \overline {D\left( t \right)} < \infty \;且\;\overline {Z\left( t \right)} < \infty $ | (14) |
即让实队列D(t)和虚队列Z(t)稳定,来保证数据队列中数据最大等待不超过接收用户的要求Tmax.
2.2 Lyapunov优化方法利用Lyapunov优化方法求解以上优化问题,该优化方法不需要知道各随机过程的概率分布的先验知识.将待求解的问题转化为最小化每个时隙的“漂移加惩罚”表达式,经整理等效于
| $ \begin{array}{*{20}{c}} {\min :V\rho {P_E}\left( t \right)\Delta t + D\left( t \right)\left[ {a\left( t \right) - \mu \left( t \right)\Delta t} \right] + }\\ {Z\left( t \right)\left[ {\sigma - \mu \left( t \right)\Delta t} \right]} \end{array} $ | (15) |
简化(15),除去决策变量P(t)的无关项,原问题则转化为
| $ \begin{array}{*{20}{c}} {\min :\rho VP\left( t \right)\Delta t - \left[ {Z\left( t \right) + D\left( t \right)} \right]\mu \left( t \right)\Delta t} \end{array} $ | (16) |
| $ {{\rm{s}}.\;{\rm{t}}.\;\;\rho P\left( t \right)\Delta t \geqslant B\left( t \right)} $ | (17) |
约束式(8)~式(10)
求解问题(16)(在式(8)~式(10)和式(17)约束下),t时隙为使得式(16)最小,用户的最佳发送功率记为P*(t),
| $ \begin{array}{*{20}{c}} {{P^*}\left( t \right) = \mathop {\arg }\limits_{P\left( t \right)⟧} \min \left\{ {\rho VP\left( t \right)\Delta t - } \right.}\\ {\left. {\frac{{\Delta t}}{2}\left[ {Z\left( t \right) + D\left( t \right)} \right]{\rm{l}}{{\rm{b}}_2}\left[ {1 + P\left( t \right)h\left( t \right)} \right]} \right\}} \end{array} $ |
求解P*(t),代入速率-功率公式(2), 对决策变量P(t)求偏导,求得
| $ {P^ * }\left( t \right) = \frac{{D\left( t \right) + Z\left( t \right)}}{{2\ln 2\rho V}} - \frac{1}{{h\left( t \right)}} $ | (18) |
从式(18)可知,发射机t时隙的最佳发送功率P*(t)跟当前队列积压D(t)、Z(t)和信道状态h(t)有关.
3 实时算法求解以上优化目标,得到的实时算法如下:
1) 自适应发送功率.任意t时隙,发射机的发送功率大小为P*(t)(由式(18)求得),但由于发射机的发送功率受限于峰值功率的约束(0≤P*(t)≤Pmax),所以t时隙发射机的实际发送功率为:min (Pmax, max(P*(t), 0));
2) 队列更新.分别根据式(1)(4)和式(12)更新数据队列、能量队列和虚拟队列,基于t+1时刻的队列积压和信道状况,用1)中决策方法进行t+1时刻发射机的发送功率.
3) 能量调度.如果t时隙ρP(t)Δt≤B(t)成立,则发射机从能量队列获取的能量为PH(t)=ρP(t)Δt,从传统电网获取的能量为PE(t)=0,即该时隙发射机不需要从传统电网获取额外能量,控制器控制发射机只从充电电池中获取能量;否则,发射机需要从能量队列和传统电网同时获取能量,控制器控制发射机分别从二者获取的能量大小为
| $ \begin{array}{*{20}{c}} {{P_H}\left( t \right) = }\\ {\rho P\left( t \right)\Delta t,{P_E}\left( t \right) = \rho P\left( t \right)\Delta t - B\left( t \right)} \end{array} $ |
定理1 假设数据到达a(t)∈Λ, t=1, 2, …,a(t)∈Λ, Λ落在问题的可行域.如果固定参数δ,0≤δ≤amax,且V>0,提出算法的性能如下.
1) 在所有的时隙中,队列D(t)和Z(t)的上确界分别为
| $ {D_{\max }} = 2\ln 2\rho V\left( {\frac{1}{{{h_{\min }}}} + {P_{\max }}} \right) + {a_{\max }} $ | (19) |
| $ {Z_{\max }} = 2\ln 2\rho V\left( {\frac{1}{{{h_{\min }}}} + {P_{\max }}} \right) + \delta $ | (20) |
2) 数据队列中数据等待服务的最大时延Tmax为
| $ {T_{\max }} = \frac{{4\ln 2\rho V\left( {\frac{1}{{{h_{\min }}}} + {P_{\max }}} \right) + {a_{\max }} + \delta }}{\delta } $ | (21) |
3) 若给定δ,且δ≤E{a(t)},基于所提出的算法,发射机额外从传统电网消耗的能量,其期望的平均值跟最优值Copt的差值不超过C/V,即
| $ \mathop {\lim }\limits_{t \to \infty } \frac{1}{t}\sum\limits_{\tau = 0}^{t - 1} {E\left\{ {\rho {P_E}\left( \tau \right)\Delta t} \right\}} \leqslant {{\rm{C}}_{opt}} + \frac{C}{V} $ | (22) |
这里C为常数.
| $ C = \frac{{\left[ {{{\left( {{a_{\max }}} \right)}^2} + {{\left( {{\mu _{\max }}\Delta t} \right)}^2}} \right]}}{2} + \frac{{\max \left[ {{\sigma ^2},{{\left( {{\mu _{\max }}\Delta t} \right)}^2}} \right]}}{2} $ |
定理1的证明可参考文献[12].从定理1可看出所提出的算法、数据队列的积压,即数据等待的时延随参数V取值增大而增大,而算法的性能(目标函数)则从传统电网消耗的能量随参数V的增大而减小. V是一个调节参数,平衡性能和时延. V的取值根据系统设计需要设置.为了减小最大等待时延Tmax,δ的值应当尽可能的大,但要满足δ≤E{a(t)},如果E{a(t)}给出,则可使δ=E{a(t)}.
3.2 算法的复杂度和优势基于Lyapunov提出的实时算法只与当前时隙D(t)、Z(t)、a(t)、b(t)和B(t)有关,因此该算法易于实现.而文献[10-11]中基于动态规划提出的最优资源分配算法其复杂度与有限的时隙个数呈指数增长,特别是对维度大的系统如多队列优化,采用动态规划其复杂度很大[10-11].此外基于动态规划的优化算法需要知道EH、数据到达以及信道状况的统计分布知识.而基于Lyapunov优化的算法则不需要知道这些随机过程的统计分布知识.
4 数值仿真考虑带宽为W=1 MHz的加性高斯衰落信道,每时隙的传输速率为
| $ \mu \left( t \right) = W{\rm{lb}}\left( {1 + h\left( t \right)P\left( t \right)} \right) $ |
其中h(t)为信道的实际增益除以噪声功率谱密度和带宽的积.太阳能和风能同时作为发射机的EH源,具体仿真参数设置如表 1所示,其中电池容量参数是根据市面上常用的蓄电池的容量大小设置的.笔者所提出动态算法不依赖EH过程、数据达到过程以及信道状态的先验知识,这里参数的设置仅方便仿真演示,该仿真在Matlab平台上进行的.
|
|
表 1 仿真参数设置 |
为了更好地评估提出的算法,将Lyapunov优化推出的算法与2种贪婪算法相比较.其中一种贪婪算法采用“立即消耗”策略,即能量队列中的能量若不能满足发射机的需求,则控制器控制发射机立即从传统电网获取不足部分的能量用于发送数据;另外一种贪婪算法采用“最后期限消耗”策略,是指发射机在某一个期限内只消耗存储在能量队列中收集的能量,若收集的能量在期限的最后时刻还不能满足发射机的需求,才从传统电网消耗能量,这里期限取值为25个时隙.
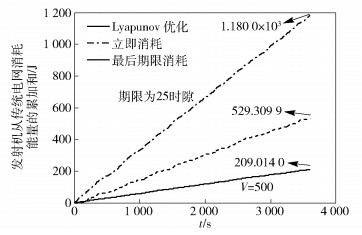
图 2示出了在1 d的时间内(3 600个时隙),3种算法下发射机从传统电网消耗的能量累加和.从图 2可以看出,Lyapunov优化算法在3种算法中性能最好,即发射机从传统电网消耗的能量最少,其原因是该方法在信道状态较好时尽可能发送更多数据.而采用“立即消耗”策略的贪婪算法性能最差,从传统电网的能耗最多,但数据队列几乎不存在等待时延.在这种参数设置下累计1 d,使用提出的算法比“立即消耗”算法可节省约971 J的能量,比“最后期限消耗”算法节省约320 J的能量.
|
图 2 3种算法下从传统电网累计能耗比较 |
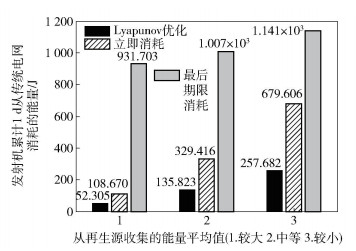
图 3所示为收集的能量平均值相对较大、中等和较小3种情况下发射机在传统电网上的总能耗(3 600个时隙末). Lyapunov优化算法相对2种贪婪算法,在每种情况下均使发射机在传统电网上的能耗最少;收集的能量平均值越大,发射机在传统电网上的能耗越少.
|
图 3 3种情况下发射机在传统电网上的总能耗 |
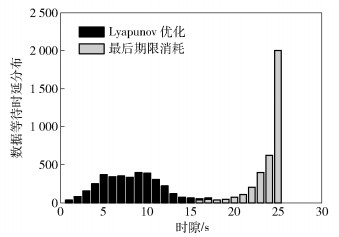
为了更好地观察提出算法给数据队列带来的时延,在保持图 2中参数不变的情况下,图 4示出了不同算法下数据队列中3 600个时隙内到达的数据等待时延分布.基于“立即消耗”策略的贪婪算法,数据几乎没有等待,但从图 2可看出该贪婪算法性能最差,图 4所示为Lyapunov优化算法和“最后期限消耗”策略的贪婪算法的比较.从图 4可以看出,使用Lyapunov优化算法数据平均等待9个时隙,而采用“最后期限消耗”策略的贪婪算法大部分数据等待25个时隙.因此Lyapunov优化算法无论在性能还是在数据等待时延上都有较大优势.
|
图 4 2种算法下数据等待时延分布 |
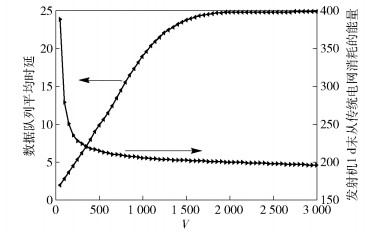
为了更清楚地了解参数V的取值对性能—时延的影响,图 5给出了参数V与算法性能和数据队列平均时延的关系.正如文中的理论分析一致,平均时延随V值的增大而非线性增加,而算法性能即发射机从传统电网消耗的能量随之下降,但当V值增加到一定值(从图 5可看出,当V值取1 500时)二者随之变化不明显,即趋于饱和,这表明参数V取值足够大时,数列平均时延达到最大值Tmax,而算法性能趋于最优值Copt.
|
图 5 参数V与算法的性能和数据队列平均时延的关系 |
研究了具有混合供电源的单用户无线通信系统的能量调度和自适应发送功率问题,在发射机不知道数据到达过程、能量收集过程以及信道状态概率分布的情况下,基于Lyapunov优化给出了一种能量调度和自适应功率算法,通过调节参数V可使发射机从传统电网消耗的平均能量趋于最小,使系统有效利用收集的清洁能量,同时保证数据队列的时延不超过用户的最大容忍时隙Tmax,该算法复杂度低,易于实现.为了评估提出的算法,仿真从不同方面与2种贪婪算法相比较,结果表明,提出算法无论在性能方面还是数据队列时延方面都优于贪婪算法.本文提出的算法具有普适性,不需要知道各随机过程的先验统计知识.此外该方法可进一步扩展至具有不同要求的多用户无线通信系统,这将作为我们下一步的研究工作.
| [1] | Ozel O, Tutuncuogluk K, Ulukus S. Fundamental limits of energy harvesting communications[J]. IEEE Communications Magazine, 2015, 53(4): 126–132. doi: 10.1109/MCOM.2015.7081085 |
| [2] | Ulukus A, Yener E, Erkip O. Energy harvesting wireless communications:a review of recent advances[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 360–381. doi: 10.1109/JSAC.2015.2391531 |
| [3] | Ozel O, Tutuncuoglu K, Yang J, et al. Transmission with energy harvesting nodes in fading wireless channels:optimal policies[J]. IEEE J Sel Areas Commun, 2011, 29(8): 1732–1743. doi: 10.1109/JSAC.2011.110921 |
| [4] | Tutuncuoglu K, Yener A. Optimum transmission policies for battery limited energy harvesting nodes[J]. IEEE Trans Wireless Commun, 2012, 11(3): 1180–1189. doi: 10.1109/TWC.2012.012412.110805 |
| [5] | Imran A, Imtiaz A, Jahangir H. Optimal stochastic power allocation and relay selection for energy harvesting systems[J]. IEEE Wireless Communications Letters, 2017, 6(4): 546–549. doi: 10.1109/LWC.2017.2715810 |
| [6] | Huang C, Zhang R, Cui S. Optimal power allocation for outage probability minimization in fading channels with energy harvesting constraints[J]. IEEE Transaction Wireless Communications, 2014, 13(2): 1074–1087. doi: 10.1109/TW.2013.121813.130953 |
| [7] | Zhang H, Huang S, Jiang C, et al. Energy efficient user association and power allocation in millimeter-wave-based ultra dense networks with energy harvesting base stations[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 1936–1947. doi: 10.1109/JSAC.2017.2720898 |
| [8] | Hu J, Heng W, Zhang G, et al. Energy efficient resource allocation in timesharing multiuser systems with hybrid energy harvesting transmitter[J]. China Communications, 2017, 14(8): 83–92. doi: 10.1109/CC.2017.8014350 |
| [9] | Ng D, Lo E, Schober R. Energy-efficient resource allocation in OFDMA systems with hybrid energy harvesting base station[J]. IEEE Trans Wireless Commun, 2013, 12(7): 3412–3427. doi: 10.1109/TWC.2013.052813.121589 |
| [10] | Ahmed I, Ikhlef A, Ng DWK. Power allocation for an energy harvesting transmitter with hybrid energy sources[J]. IEEE Transactions on Wireless Communications, 2013, 12(12): 6255–6267. doi: 10.1109/TWC.2013.111013.130215 |
| [11] |
周文辉, 仲伟峰, 余荣. 微电网中面向用户的自适应能量调度策略[J]. 北京邮电大学学报, 2015, 38(3): 77–81.
Zhou Wenhui, Zhong Weifeng, Yu Rong. An adaptive energy scheduling strategy for electricity consumers in micro grid[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(3): 77–81. |
| [12] | Neely M J. Stochastic network optimization with application to communication and queueing systems[M]. America: Morgan & Claypool Publishers, 2010. |


