2. 山东交通学院 信息科学与电气工程学院, 济南 250357
针对单天线单用户频谱感知性能严重恶化的问题.为了进一步提高频谱检测性能,减小感知数据传输开销,提出了两步协作频谱感知方案.仿真结果表明,提出的基于平方率合并的软合并两步协作频谱感知方案,克服了多径衰落、阴影衰落和接收机不稳定的问题,大大提高了频谱检测可靠性,具有软合并协作和硬合并协作的优点,减小了网络负载,同时提高了检测性能.
2. School of Information and Science and Electrical Engineering, Shandong Jiaotong University, Jinan 250357, China
In the cognitive radio network, the performance of spectrum sensing by a single user with a single antenna may degrade significantly. In order to improve the detection performance and reduce spectrum sensing data transmission overhead, a two step cooperative spectrum sensing scheme was proposed. Simulations show that proposed scheme can significantly improve the detection reliability by overcoming multi-path fading, shadowing and the receiver uncertainty problem. The proposed scheme combines the advantages of the soft combination and the hard combination schemes. In addition, it will reduce the network overload and improves the detection performance.
在认知无线电网络中[1],由于无线应用的爆炸式增长,频谱资源不能满足无线应用日益增长的需求.然而,当前的大多数无线网络是以固定频谱分配为特征的.研究表明,固定频谱分配政策加剧了频谱利用率不高的结果,因此,通常认为不是频谱资源有限而是频谱利用率不高.
为了克服当前频谱利用率不高的困境,认知无线电[1-2]技术应运而生.频谱感知是认知无线电技术的一个重要功能.在无线信道中,对于单天线的认知用户,严重的阴影衰落和多径衰落将导致频谱感知性能的恶化, 因此,多天线或多用户的协作频谱感知被认为是提高频谱检测可靠性的有效方法.
经典的基于中心的协作频谱感知方案有两种:硬合并协作方案和软合并协作方案.常用的硬合并协作判决规则有逻辑AND、逻辑OR和逻辑MAJORITY. Ghasemi等[3]分析了逻辑OR硬合并协作方案,Peh E等[4]分析研究了逻辑OR和逻辑AND两个硬合并协作方案.硬合并协作方案只在网络中传输1 bit硬判决信息,优点是只需要有限的带宽,网络负载小;缺点是检测概率低.
常用的软合并协作方案有:平方率合并(SLC, square law combining)方案、平方率选择(SLS, square law selection)方案、最大比合并(MRC, maximal ratio combining)方案, 等增益合并(EGC, equal gain combining)方案等. Liu[5]等研究了平方率合并方案并分析了协作频谱感知性能.在没有信道状态信息的情况下,平方率合并方案呈现出良好的检测性能. Nallagonda[6]等分析了最大比合并方案的频谱感知性能,在有信道状态信息的情况下,最大比合并方案呈现出更好的检测性能. Sun[7]等研究了认知无线网络中的分集接收方案.软合并协作方案需要在网络中传输天线感知信息,缺点是需要较宽的带宽,网络负载大;优点是检测概率高.
基于硬合并协作和软合并协作方案的检测性能,提出了一个两步复合协作频谱感知方案:第1步,在有多天线认知用户接收机执行软合并协作;第2步,在融合中心执行硬合并协作.
在两步复合协作方案中,软合并协作频谱感知是指一个有多天线的认知用户基于软合并方案感知主用户.在软合并协作过程中,认知用户收集所有天线上的感知信息,用各种软合并协作方案得到主用户是否占用频段的1 bit局部判决.硬合并协作频谱感知是指有多天线的多个认知用户在软合并协作的基础上,基于硬合并协作方案感知主用户.在硬合并协作过程中,多个有多天线认知用户把软合并协作阶段的1 bit主用户是否占用频段的局部判决发送到融合中心,在融合中心通过硬合并协作方案做出主用户是否占用频段的全局判决.
考虑SLC、SLS、MRC 3种软合并协作方案的研究结果显示:SLC和SLS软合并方案是2种低复杂度的分集技术,与SLS相比,SLC方案呈现出更好的检测性能. MRC合并方案需要知道信道状态信息, 因此,在软合并协作频谱感知阶段,应选择SLC软合并协作方案.
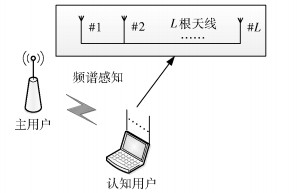
1 两步协作频谱感知系统模型和算法 1.1 软合并协作频谱感知系统模型软合并协作频谱感知系统模型如图 1所示,可以看出,主用户有1根天线,认知用户有L根天线,假定主用户天线和认知用户第l根天线之间的信道是Nakagami-m衰落信道,m是衰落因子,信道的增益是hl,当主用户占用频段时,从认知用户的第l根天线收到的信号可以表示为
| $ {r_l}\left( t \right) = {h_l}s\left( t \right) + n\left( t \right) $ | (1) |
|
图 1 软合并协作频谱感知系统模型 |
其中:n(t)是加性高斯白噪声(AWGN,additive white Gaussian noise), s(t)表示从主用户发送的信号,rl(t)表示认知用户第l根天线收到的信号.
当主用户占用频段时,认知用户接收主用户信号,根据来自认知用户天线上的主用户信号, 认知用户执行软合并协作频谱感知方案,获得主用户是否占用频段的局部判决.在认知无线电网络,有多个多天线认知用户,他们获得了主用户是否存在的局部判决.
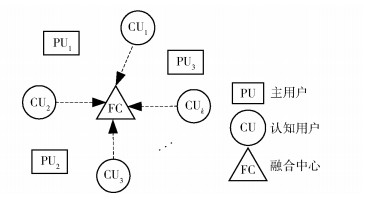
1.2 硬合并协作频谱感知系统模型硬合并协作频谱感知系统模型如图 2所示[8],由系统模型图可以看出,认知用户分布在网络中不同的位置,他们相互协作以检测主用户的行为.在软合并协作频谱感知阶段,每个认知用户独立地执行软合并协作频谱感知方案获得了1 bit的主用户是否存在的局部判决.在软合并协作频谱感知的基础上,在硬合并协作频谱感知阶段,每个多天线认知用户通过二进制编码发送1 bit局部判决到信息融合中心.在融合中心,通过执行硬合并协作方案:逻辑OR、逻辑AND和逻辑MAJORITY获得主用户是否存在的全局判决.
|
图 2 硬合并协作频谱感知系统模型 |
根据两步协作频谱感知方案,算法步骤如下.
步骤1 选择软合并协作方案,在多天线认知用户网络中,根据SLC、SLS、MRC软合并协作方案的特征,选择SLC软合并方案.
步骤2 执行软合并协作方案,每个有多天线的认知用户执行SLC软合并方案,得到主用户是否占用频段的1 bit局部判决.
步骤3 传递软合并协作结果,每个有多天线的认知用户传递主用户是否占用频段的1 bit局部判决到融合中心.
步骤4 执行硬合并协作方案,在融合中心,执行硬合并协作规则:逻辑OR、逻辑AND和逻辑MAJORITY获得主用户是否占用频段的全局判决.
2 有多天线的认知用户基于SLC的软合并协作频谱感知由于SLC合并方案没有相关检测过程,减少了接收机的复杂度,所以软合并协作频谱感知阶段选择平方率合并技术为软合并协作频谱感知方案.
SLC是一个简单的线性合并方案,在此方案中,通过计算每个天线分支上信号的平方和,得到一个判决统计
| $ {E_{{\rm{SLC}}}} \sim \left\{ \begin{array}{l} x_{2Lu}^2,{H_0}\\ x_{2Lu}^2\left( {2{y_{{\rm{SLC}}}}} \right),{H_1} \end{array} \right. $ | (2) |
其中:x2Lu2和x2Lu2(2ySLC)表示中心的和非中心的卡方分布,它们的自由度是2Lu, x2Lu2(2ySLC)有一个非中心的参数2ySLC.这里,
在非衰落的AWGN信道,假定噪声方差是1,能量检测器的虚警概率可表示为[10]
| $ {P_f} = \frac{{\Gamma \left( {u,\lambda /2} \right)}}{{\Gamma \left( u \right)}} $ | (3) |
其中:λ为判决阈值,Γ(·)和Γ(·, ·)分别是完整和不完整的Gamma函数.
在非衰落的AWGN信道,能量检测器的检测概率可表示为
| $ {P_{\rm{d}}} = {Q_u}\left( {\sqrt {2y} ,\sqrt \lambda } \right) $ | (4) |
其中:u(·, ·)为普遍Marcum Q函数,y为信噪比.
漏检概率经常被用来评估检测性能,它与检测概率的关系可表示为
| $ {P_{\rm{m}}} = 1 - {P_{\rm{d}}} $ | (5) |
在这里,用另一种形式的普遍Marcum Q函数表达检测概率Pd,其表达式为[11]
| $ {P_{\rm{d}}}\left( {y,\lambda } \right) = 1 - \sum\limits_0^\infty {\frac{{\gamma \left( {n + u,\lambda /2} \right)}}{{\Gamma \left( {n + u} \right)n!}}{y^n}{{\rm{e}}^{ - y}}} $ | (6) |
其中γ(α, x)表示低阶不完整Gamma函数.
在AWGN信道,由式(2)(3)和(6),基于SLC软合并协作频谱感知方案,虚警概率和检测概率分别表示为
| $ {P_{{\rm{f}},{\rm{SLC}}}} = \frac{{\Gamma \left( {Lu,\lambda /2} \right)}}{{\Gamma \left( {Lu} \right)}} $ | (7) |
| $ \begin{array}{*{20}{c}} {{P_{{\rm{d,SLC}}}} = {Q_{Lu}}\left( {\sqrt {2{y_{{\rm{SLC}}}}} ,\sqrt \lambda } \right) = }\\ {1 - \sum\limits_{n = 0}^\infty {\frac{{\gamma \left( {n + u,\lambda /2} \right)}}{{\Gamma \left( {n + u} \right)n!}}{{\left( {{y_{{\rm{SLC}}}}} \right)}^n}{{\rm{e}}^{ - {y_{{\rm{SLC}}}}}}} } \end{array} $ | (8) |
对于独立同分布的衰落信道,平均检测概率可通过下面的积分来评估[7],积分函数为Pd, SLC和信噪比概率密度函数f(ySLC)的乘积.
| $ {{\bar P}_{{\rm{d,SLC}}}} = \int_0^\infty {{P_{{\rm{d,SLC}}}}\left( {{y_{{\rm{SLC}}}},\lambda } \right)f\left( {{y_{{\rm{SLC}}}}} \right){\rm{d}}{y_{{\rm{SLC}}}}} ,{y_{{\rm{SLC}}}} > 0 $ | (9) |
其中:f(ySLC)为输出信噪比ySLC的概率密度函数(PDF,probability dense function),对于独立同分布的Nakagami-m衰落信道,表达式为[12]
| $ f\left( {{y_{{\rm{SLC}}}}} \right) = \frac{{{m^{Lm}}{{\left( {{y_{{\rm{SLC}}}}} \right)}^{Lm}}}}{{{{\left( {{{\bar y}_{{\rm{SLC}}}}} \right)}^{Lm}}\Gamma \left( {Lm} \right)}}{{\rm{e}}^{ - \frac{m}{{{{\bar y}_{{\rm{SLC}}}}}}{y_{{\rm{SLC}}}}}},{y_{{\rm{SLC}}}} > 0 $ | (10) |
其中:ySLC是平均信噪比,m是衰落因子.
由式(8)~(10)得
| $ \begin{array}{*{20}{c}} {{{\bar P}_{{\rm{d,SLC}}}} = 1 - \frac{{{m^{Lm}}}}{{\Gamma Lm{{\left( {{{\bar y}_{{\rm{SLC}}}}} \right)}^{Lm}}}}\sum\limits_{n = 0}^\infty {\frac{{\gamma \left( {n + Lu,\frac{\lambda }{2}} \right)}}{{\Gamma \left( {n + Lu} \right)n!}}} \times }\\ {\int_0^\infty {{{\left( {{y_{{\rm{SLC}}}}} \right)}^{n + Lm - 1}}{{\rm{e}}^{ - \frac{{m + {{\bar y}_{{\rm{SLC}}}}}}{{{{\bar y}_{{\rm{SLC}}}}}}{y_{{\rm{SLC}}}}}}{\rm{d}}{y_{{\rm{SLC}}}}} } \end{array} $ | (11) |
由文献[13]可得检测概率为
| $ {{\bar P}_{{\rm{d,SLC}}}} = 1 - B\left( {Lu,Lm,L{{\bar y}_{{\rm{SLC}}}}} \right) $ | (12) |
其中
| $ \begin{array}{*{20}{c}} {B\left( {\alpha ,\beta ,x} \right) = }\\ {{{\left( {\frac{\beta }{{\beta + x}}} \right)}^\beta }\sum\limits_0^\infty {\frac{{\gamma \left( {n + \alpha ,\lambda /2} \right){{\left( \beta \right)}_n}}}{{\Gamma \left( {n + \alpha } \right)n!}}{{\left( {\frac{x}{{\beta + x}}} \right)}^n}} } \end{array} $ | (13) |
其中
在软合并协作频谱感知阶段,每个有多天线的认知用户通过SLC软合并方案得到1 bit主用户是否存在的局部判决,使感知数据传输开销最小.在硬合并协作频谱感知阶段,每个有多天线的认知用户传输1 bit局部判决到融合中心.在融合中心,通过执行硬合并协作频谱感知方案得到主用户是否存在的全局判决.
在融合中心,执行“N中取k”硬合并规则,检测概率和虚警概率可以分别表示为
| $ {P_{\rm{D}}} = \sum\limits_{i = k}^n {C_N^i{{\left( {{P_{{\rm{d}},i}}} \right)}^i}{{\left( {1 - {P_{{\rm{d}},i}}} \right)}^{N - i}}} $ | (14) |
| $ {P_{\rm{F}}} = \sum\limits_{i = k}^n {C_N^i{{\left( {{P_{{\rm{f}},i}}} \right)}^i}{{\left( {1 - {P_{{\rm{f}},i}}} \right)}^{N - i}}} $ | (15) |
其中Pd, i和Pf, i是每个认知用户的检测概率和虚警概率.在同样的条件下,假定各个认知用户有相同的检测概率和虚警概率.
| $ {P_{{\rm{d}},i}} = {P_{\rm{d}}} = {P_{{\rm{rob}}}}\left( {E > \lambda \left| {{H_1}} \right.} \right) $ | (16) |
| $ {P_{{\rm{f}},i}} = {P_{\rm{f}}} = {P_{{\rm{rob}}}}\left( {E > \lambda \left| {{H_0}} \right.} \right) $ | (17) |
当k=1, k=N, k>
根据提出的两步复合协作频谱感知方案,在SLC软合并的基础上,3种硬合并协作频谱感知方案分析如下.
3.1 逻辑OR硬合并协作融合每个认知用户发送1 bit局部判决到融合中心,在融合中心,主用户是否存在的全局判决通过逻辑OR规则判决获得.在逻辑OR规则中,只要有1个认知用户的局部判决是逻辑1, 融合中心的全局判决就是逻辑1.
假定所有的认知用户是独立的,在逻辑OR判决规则下,检测和虚警概率分别表达为[14]
| $ {P_{{\rm{D}},{\rm{OR}}}} = 1 - \prod\limits_{i = 1}^N {\left( {1 - {P_{{\rm{d}},i}}} \right)} = 1 - {\left( {1 - {P_{\rm{d}}}} \right)^N} $ | (18) |
| $ {P_{{\rm{F}},{\rm{OR}}}} = 1 - \prod\limits_{i = 1}^N {\left( {1 - {P_{{\rm{f}},i}}} \right)} = 1 - {\left( {1 - {P_{\rm{f}}}} \right)^N} $ | (19) |
漏检概率表示为
| $ {P_{{\rm{M}},{\rm{OR}}}} = 1 - {P_{{\rm{D}},{\rm{OR}}}} = \prod\limits_{i = 1}^N {\left( {1 - {P_{{\rm{d}},i}}} \right)} = 1 - {\left( {1 - {P_{\rm{d}}}} \right)^N} $ | (20) |
由式(12)和式(18)可知,在逻辑OR判决规则下,全局检测概率为
| $ \begin{array}{l} {{\bar P}_{{\rm{D}},{\rm{OR}}}} = 1 - \prod\limits_{i = 1}^N {\left( {1 - {P_{{\rm{d}},i}}} \right)} = 1 - {\left( {1 - {P_{\rm{d}}}} \right)^N} = \\ 1 - {\left( {1 - {{\bar P}_{{\rm{d,SLC}}}}} \right)^N} = 1 - {\left( {B\left( {Lu,Lm,L{{\bar y}_{{\rm{SLC}}}}} \right)} \right)^N} \end{array} $ | (21) |
每个认知用户发送1 bit局部判决到融合中心,在逻辑AND规则中,只有所有认知用户的局部判决是逻辑1, 融合中心的全局判决才能是逻辑1.
假定所有的认知用户是独立的,在逻辑AND判决规则下,检测和虚警概率分别为[15]
| $ {P_{{\rm{D}},{\rm{AND}}}} = \prod\limits_{i = 1}^N {{P_{{\rm{d}},i}}} = {\left( {{P_{\rm{d}}}} \right)^N} $ | (22) |
| $ {P_{{\rm{F}},{\rm{AND}}}} = \prod\limits_{i = 1}^N {{P_{{\rm{f}},i}}} = {\left( {{P_{\rm{f}}}} \right)^N} $ | (23) |
漏检概率表示为
| $ {P_{{\rm{M}},{\rm{AND}}}} = 1 - {P_{{\rm{D}},{\rm{AND}}}} = 1 - \prod\limits_{i = 1}^N {{P_{{\rm{d}},i}}} = 1 - {\left( {{P_{\rm{d}}}} \right)^N} $ | (24) |
由式(12)和式(22),在逻辑AND判决规则下,全局检测概率为
| $ \begin{array}{*{20}{c}} {{{\bar P}_{{\rm{D}},{\rm{AND}}}} = \prod\limits_{i = 1}^N {{P_{{\rm{d}},i}}} = {{\left( {{P_{\rm{d}}}} \right)}^N} = }\\ {{{\left( {{{\bar P}_{{\rm{d}},{\rm{SLC}}}}} \right)}^N} = {{\left( {1 - B\left( {Lu,Lm,L{{\bar y}_{{\rm{SLC}}}}} \right)} \right)}^N}} \end{array} $ | (25) |
在逻辑MAJORITY规则中,如果超过一半认知用户的局部判决是逻辑1, 那么融合中心的全局判决是逻辑1.
假定所有的认知用户是独立的,在逻辑MAJORITY判决规则下,检测、虚警概率和漏检概率分别为[16]
| $ \begin{array}{*{20}{c}} {{P_{{\rm{D}},{\rm{MAJOR}}}} = \sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{{\rm{d}},i}}} \right)}^i}{{\left( {1 - {P_{{\rm{d}},i}}} \right)}^{N - i}}} = }\\ {\sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{\rm{d}}}} \right)}^i}{{\left( {1 - {P_{\rm{d}}}} \right)}^{N - i}}} } \end{array} $ | (26) |
| $ \begin{array}{*{20}{c}} {{P_{{\rm{F}},{\rm{MAJOR}}}} = \sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{{\rm{f}},i}}} \right)}^i}{{\left( {1 - {P_{{\rm{f}},i}}} \right)}^{N - i}}} = }\\ {\sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{\rm{f}}}} \right)}^i}{{\left( {1 - {P_{\rm{f}}}} \right)}^{N - i}}} } \end{array} $ | (27) |
| $ \begin{array}{*{20}{c}} {{P_{{\rm{M}},{\rm{MAJOR}}}} = 1 - {P_{{\rm{D}},{\rm{MAJOR}}}} = }\\ {1 - \sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{{\rm{d}},i}}} \right)}^i}{{\left( {1 - {P_{{\rm{d}},i}}} \right)}^{N - i}}} = }\\ {1 - \sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{\rm{d}}}} \right)}^i}{{\left( {1 - {P_{\rm{d}}}} \right)}^{N - i}}} } \end{array} $ | (28) |
由式(12)和式(26),在逻辑MAJORITY判决规则下,全局检测概率如下
| $ \begin{array}{*{20}{c}} {{{\bar P}_{{\rm{D}},{\rm{MAJOR}}}} = \sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{{\rm{d}},i}}} \right)}^i}{{\left( {1 - {P_{{\rm{d}},i}}} \right)}^{N - i}}} = }\\ {\sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{P_{\rm{d}}}} \right)}^i}{{\left( {1 - {P_{\rm{d}}}} \right)}^{N - i}}} = }\\ {\sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {{{\bar P}_{{\rm{d,SLC}}}}} \right)}^i}{{\left( {1 - {{\bar P}_{{\rm{d,SLC}}}}} \right)}^{N - i}}} = }\\ {\sum\limits_{i = \frac{N}{2}}^N {C_N^i{{\left( {1 - B\left( {Lu,Lm,L\bar y} \right)} \right)}^i}} \times }\\ {{{\left( {B\left( {Lu,Lm,L{{\bar y}_{{\rm{SLC}}}}} \right)} \right)}^{N - i}}} \end{array} $ | (29) |
通过仿真并与经典的硬合并协作频谱感知比较来评估两步协作频谱感知方案的性能.
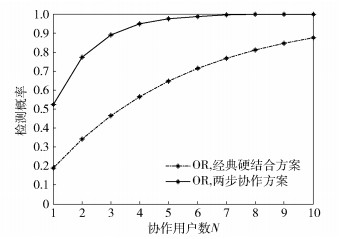
图 3为基于SLC软合并协作、逻辑OR硬合并的两步协作频谱感知检测概率对协作认知用户数的性能比较曲线.比较经典硬合并协作方案和两步协作频谱感知方案.仿真参数如下:信噪比为1 dB,u=2,m=3,天线数L=1,L=2.由图 3可以看出,两步协作频谱感知方案的检测概率比经典硬合并检测方案的检测概率约高0.34.例如,当N=2时,经典硬合并检测方案的检测概率是0.34;而当N=2时,两步协作频谱感知方案的检测概率是0.78.同样地,当N=4时,经典硬合并检测方案检测概率是0.58;而当N=4时,两步协作频谱感知方案的检测概率是0.97.因此,图 3表明,随着协作用户数和分集天线数的增加,频谱检测性能有了显著的改善.
|
图 3 检测概率对协作用户数性能比较曲线 |
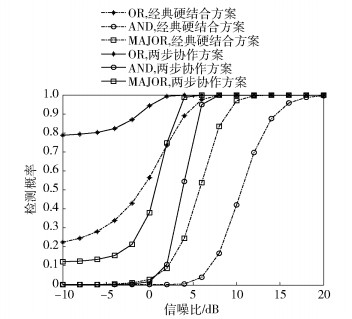
图 4为基于SLC软合并协作、逻辑OR、逻辑AND和逻辑MAJORITY硬合并的两步协作频谱感知检测概率对信噪比的性能比较曲线.比较了经典硬合并协作方案和两步协作频谱感知方案.仿真参数如下:N=5,u=2,m=3,天线数L=1,L=2.从图 4可以看出,在低信噪比、逻辑OR规则下,两步协作频谱感知方案的检测概率比经典硬合并检测方案的检测概率约高0.50.例如,当信噪比为-10 dB时,经典硬合并协作方案的检测概率是0.22;而当信噪比为-10 dB时,两步协作频谱感知方案的检测概率是0.80.同样地,当信噪比为-5 dB时,经典硬合并协作方案的检测概率是0.31;而当信噪比为-5 dB时,两步协作频谱感知方案的检测概率是0.81.从图 4还可以发现,在逻辑AND融合规则下,可获得同样的检测概率,两步协作频谱感知方案比经典硬合并检测方案有7 dB的分集增益.同样地,在逻辑MAJORITY融合规则下,可获得同样的检测概率,两步协作频谱感知方案比经典硬合并检测方案有5 dB的分集增益.因此,图 4表明,随着信噪比和分集天线数的增加,检测概率有了显著的提高.
|
图 4 不同方案的检测概率与信噪比比较 |
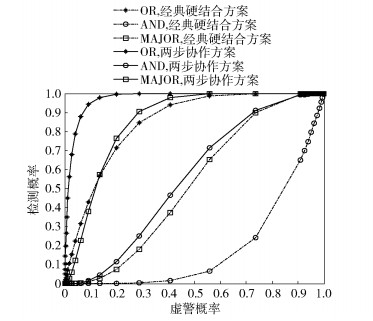
图 5为基于SLC软合并协作、逻辑OR、逻辑AND和逻辑MAJORITY硬合并的两步协作频谱感知检测概率对虚警概率的性能比较曲线.比较了经典硬合并协作方案和两步协作频谱感知方案.仿真参数如下:信噪比为-10 dB,N=5,u=2,m=3, 天线数L=1,L=2.从图 5可以看出,随着虚警概率的增加,检测概率有显著提高.与经典的硬合并方案相比,两步协作频谱感知呈现出更好的检测性能.例如,当虚警概率是0.2时,在逻辑OR规则下,检测概率两步协作方案比经典硬合并方案高约0.3.同样地,在逻辑AND规则和逻辑MAJORITY规则下,检测概率两步协作方案比经典硬合并方案分别高约0.1和0.7.
|
图 5 检测概率对虚警概率性能比较曲线 |
协作频谱感知是提高频谱感知性能的一个有效方法.考虑到单天线认知用户的软合并协作频谱感知和硬合并协作频谱感知的局限性,提出了一个两步协作频谱感知方案.在提出的方案中,天线感知信息不直接在网络中传输,与经典软合并方案相比,减小了网络数据传输开销.仿真结果显示,与经典硬合并方案相比,提出的两步协作频谱感知方案进一步提高了检测性能.
| [1] | Akyildiz I F, Lee W Y, Vuran M C, et al. Next generation/dynamic spectrum access/cognitive radio wireless networks:a survey[J]. Computer Networks, 2006, 50(13): 2127–2159. doi: 10.1016/j.comnet.2006.05.001 |
| [2] | Akyildiz I F, Lee W Y, Chowdhury K R. CRAHNs:cognitive radio Ad hoc networks[J]. Ad Hoc Networks, 2009, 7(5): 810–836. doi: 10.1016/j.adhoc.2009.01.001 |
| [3] | Ghasemi A, Sousa E S. Collaborative spectrum sensing for opportunistic access in fading environments[C]//First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Baltimore: IEEE Press, 2005: 131-136. |
| [4] | Peh E, Liang Y C. Optimization for cooperative sensing in cognitive radio networks[C]//IEEE Wireless Communications and Networking Conference. Kowloon: IEEE Press, 2007: 27-32. |
| [5] | Liu Yunxue, Yuan Dongfeng, Jiang Mingyan, et al. Analysis of square-law combining for cognitive radios over Nakagami chananels[C]//5th International Conference on Wireless Communications, Networking and Mobile Computing. Beijing: IEEE Press, 2009: 1-4. |
| [6] | Nallagonda S, Roy S D, Kundu S, et al. Performance of MRC fusion-based cooperative spectrum sensing with censoring of cognitive radios in rayleigh fading channels[C]//9th International Wireless Communications and Mobile Computing Conference. Sardinia: IEEE Press, 2013: 30-35. |
| [7] | Sun H J, Nallanathan A, Jiang J, et al. Cooperative spectrum sensing with diversity reception in cognitive radios[C]//6th International ICST Conference on Communications and Networking in China. Harbin: IEEE Press, 2011: 216-220. |
| [8] | Lai J, Dutkiewicz E, Liu R P, et al. Performance optimization of cooperative spectrum sensing in cognitive radio networks[C]//Wireless Communications and Networking Conference. [S. l. ]: IEEE Press, 2013: 631-636. |
| [9] | Ma Jun, Zhao Guodong, Li Ye. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(11): 4502–4507. doi: 10.1109/T-WC.2008.070941 |
| [10] | Digham F F, Alouini M S, Simon M K. On the energy detection of unknown signals over fading channels[J]. IEEE Transactions on Communications, 2007, 55(1): 21–24. doi: 10.1109/TCOMM.2006.887483 |
| [11] | Brennan L, Reed I. A recursive method of computing the Q function[J]. IEEE Transactions on Information Theory, 1965, 11(2): 312–313. doi: 10.1109/TIT.1965.1053761 |
| [12] | Simon M K, Alouini M S. Digital communication over fading channels[M]. New York: John Wiley & Sons, 2004. |
| [13] | Gradshteyn I S, Ryzhik I M. Table of integrals, series and products[M]. Jeffrey A, Ed. New York: Academic Press, 2007: 1157-1160. |
| [14] | Ghasemi A, Sousa E S. Collaborative spectrum sensing for opportunistic access in fading environments[C]//First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Baltimore: IEEE Press, 2005: 131-136. |
| [15] | Visotsky E, Kuffner S, Peterson R. On collaborative detection of TV transmissions in support of dynamic spectrum sharing[C]//First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Baltimore: IEEE Press, 2005: 338-345. |
| [16] | Aalo V, Viswanathan R. Asymptotic performance of a distributed detection system in correlated Gaussian noise[J]. IEEE Transactions on Signal Processing, 1992, 40(1): 211–213. doi: 10.1109/78.157195 |


