2. 桂林电子科技大学 认知无线电与信号处理教育部重点实验室, 广西 桂林 541004
在多基站协作通信系统中,针对基站与用户间距离差异将导致用户接收信号的异步干扰的问题,提出一种基于粒子群优化算法的异步干扰抑制预编码设计.该设计将预编码矩阵转化为寻优粒子位置参数矩阵,通过粒子间智能学习更新优化位置参数,调节适应度函数,最大化用户信干噪比,抑制异步干扰.数值分析结果表明,相对于改进的块对角化算法,所提算法使系统总速率提高了2~7 bit/s,且具有很好的收敛性.
2. Key Laboratory of Cognitive Radio and Information Processing(Guilin University of Electronic Technology), Ministry of Education, Guangxi Guilin 541004, China
In multi-base station cooperative systems, the distances are different between the base stations and the users which will result in asynchronous interference of users received signals. To suppress asynchronous interference, a pre-coding design for muti-base station cooperative communication is proposed based on particle swarm optimization algorithm. The pre-coding design converts the pre-coding matrixes into the position parameters matrixes of the optimization particle, updates the optimization position parameters by intelligent learning among the particles, and adjusts the fitness function to maximize the signal to interference plus noise ratio of user. Thus, the pre-coding design can be used to suppress asynchronous interference of users received signals. Numerical simulations show that, compared with the improved block diagonalization algorithm, the proposed algorithm the proposed algorithm will increase the sum rate of system 2~7 bit/s with a good convergence.
多基站协作可以大幅改善边缘小区用户的通信干扰问题[1]. Li等[2]提出了一种多基站协作下的混合协调策略. Heng等[3]提出了一种基于友好算法的动态聚类多基站协作方案. Sun等[4]将干扰对齐波束成形和快速多用户贪婪搜索算法相结合来抑制用户干扰. Hsu等[5]研究了多基站协作技术在多天线正交频分复用系统中的应用.
然而,在多基站协作通信系统中,用户接收的期望信号与干扰信号之间存在固有的异步干扰问题[6-7].尽管Wang等[8]研究了块对角化预编码算法,可消除异步干扰,但复杂度较高.
综上,给出了一种基于粒子群优化算法的预编码设计方法,该方法能够优化每个用户的速率,并通过迭代求得最优的预编码矩阵,来降低信号异步干扰对多基站协作通信系统性能的影响.
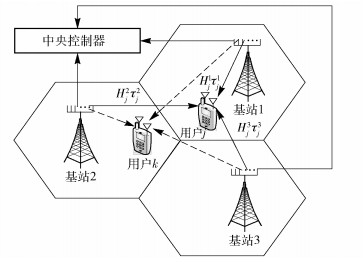
1 系统模型多基站协作系统模型如图 1所示.假设系统中有K个用户随机分布在由M个基站构成的多小区中,其中每个基站有Nt根发射天线,每个移动用户有Nr根接收天线.
|
图 1 多基站协作系统模型 |
在多基站协作的下行链路中协作的基站联合向每个移动用户发送Lj×1个数据流,不同的传输路径是相互独立的,且信道为频率平坦衰落的瑞利信道.假设每个基站能够获得每个用户信道的完美状态信息[9-11],包括各传输路径的延时.
用sj(m)表示在时刻m协作基站向用户j联合传输的维数为Lj×1的数据流,其服从均值为0,方差为1的复高斯分布;Tjb表示从基站b(b=1, 2, …, M)到用户j的传输矢量的预编码矩阵,维数为Nt×Lj,即传输矢量为xjb=Tjbsj(m);Tj表示所有基站到用户j的预编码矩阵;Hjb表示从基站b到用户j的传输信道矩阵,其元素是复高斯的独立同分布变量;Hj表示所有基站到用户j的传输信道矩阵.为了以下分析方便,假设各基站发射给每个用户的功率相同,即P1=P2=…=PK=P0.
当不考虑用户之间的异步干扰时,用户j在m时刻接收到的信号为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_j}\left( m \right) = {\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{s}}_j}\left( m \right) + \sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {\sum\limits_{b = 1}^M {\mathit{\boldsymbol{H}}_j^b\mathit{\boldsymbol{T}}_k^b{\mathit{\boldsymbol{s}}_k}\left( m \right)} } + {\mathit{\boldsymbol{n}}_j}\left( m \right) = }\\ {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{s}}_j}\left( m \right) + \sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_k}{\mathit{\boldsymbol{s}}_k}\left( m \right)} + {\mathit{\boldsymbol{n}}_j}\left( m \right)} \end{array} $ | (1) |
| $ {\rm{s}}.\;{\rm{t}}.\;\;\text{tr}\left( {{\mathit{\boldsymbol{T}}_j}\mathit{\boldsymbol{T}}_j^{\rm{H}}} \right) \le M{p_0},j = 1,2, \cdots ,K $ | (2) |
其中:tr(·)表示求矩阵迹的运算Hj=[Hj1, Hj2, …, HjM],Tj=[Tj1H, Tj2H, …, TjMH]H.
式(1)中,第1项表示用户的期望信号,第2项表示干扰信号,第3项表示噪声且E[nj(m)nj(m)H]=N0INr(N0为高斯白噪声功率).而且,发射信号满足以下特性:
| $ E\left[ {{s_j}\left( m \right){s_k}{{\left( m \right)}^{\rm{H}}}} \right] = \left\{ \begin{array}{l} {I_{{L_j}}},\;\;\;\;\;\;\;k = j\\ {O_{{L_j}}},\;\;\;\;\;\;k \ne j \end{array} \right. $ | (3) |
其中:ILj为用户j数量满足k随机分布时的取值,OLj为用户j数量不满足k随机分布时的取值.
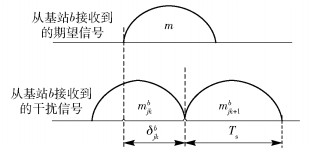
2 信号传输的异步干扰特性在实际系统中,由于基站和用户之间地理位置差异,通过定时提前机制不能保证用户接收到的干扰信号与期望信号同步,这样就产生了异步干扰. 图 2所示为信号的异步干扰特性模型[12].
|
图 2 信号的异步干扰特性模型 |
τjb表示从基站b到用户j的传输时延,bj表示用户j的服务基站,τjbj表示从基站bj到用户j的传输时延,则相对于服务基站bj其余协作基站b传输给用户j信号的时延差为Δτjb=τjb-τjbj,采用定时提前机制对时延差进行补偿,从而使得所有基站发送到用户j的时延均为τjbj,即所有基站发送给用户j的信号是同步的.然而,定时提前机制不能完全同步所有基站发送给用户k的信号对用户j产生的干扰,如图 2所示,用户j在m时刻的异步干扰信号ikjb(m)主要取决于2个相邻时刻mkjb和mkjb+1由基站b发送给用户k的信号sk(mkjb)和sk(mkjb+1),定时提前差异为
| $ \tau _{kj}^b = \left( {\tau _j^b - \Delta \tau _k^b} \right) - \tau _j^{{b_j}} = \Delta \tau _j^b - \Delta \tau _k^b $ | (4) |
假设用δkjb(0≤δkjb≤Ts)表示[τkjb/Ts],即δkjb=τkjbmod Ts,则
| $ i_{kj}^b\left( m \right) = \rho \left( {\delta _{kj}^b - {T_{\rm{s}}}} \right){\mathit{\boldsymbol{s}}_j}\left( {m_{kj}^b} \right) + \rho \left( {\delta _{kj}^b} \right){\mathit{\boldsymbol{s}}_j}\left( {m_{kj + 1}^b} \right) $ | (5) |
其中
为了简化分析,假设每个基站到同一用户的时延相等[7].因此,每个基站到同一用户的延迟相等,即τjb与b无关,用τj表示,这样τkjb也与b无关,用τkj表示,δkjb用δkj表示,ikjb(m)用ikj(m)表示,则式(5)可以表示为
| $ {i_{kj}}\left( m \right) = \rho \left( {{\delta _{kj}} - {T_{\rm{s}}}} \right){\mathit{\boldsymbol{s}}_j}\left( {{m_{kj}}} \right) + \rho \left( {{\delta _{kj}}} \right){\mathit{\boldsymbol{s}}_j}\left( {{m_{kj + 1}}} \right) $ | (6) |
由式(6)可知
| $ E\left[ {{i_{kj}}\left( m \right)} \right] = 0,\forall j,k \in \left\{ {1,2, \cdots ,K} \right\} $ | (7) |
| $ \begin{array}{*{20}{c}} {E\left[ {{i_{{k_1}j}}\left( m \right){i_{{k_2}j}}{{\left( m \right)}^{\rm{H}}}} \right] = 0,}\\ {\forall j,k \in \left\{ {1,2, \cdots ,K} \right\} \cup {k_1} \ne {k_2} \ne j} \end{array} $ | (8) |
| $ E\left[ {{i_{kj}}\left( m \right){i_{kj}}{{\left( m \right)}^{\rm{H}}}} \right] = \left\{ \begin{array}{l} {\rho ^2}\left( {{\delta _{kj}}} \right) + {\rho ^2}\left( {{\delta _{kj}} - {T_{\rm{s}}}} \right){I_{{L_\text{j}}}},\;\;\;\;k \ne j\\ {I_{{L_\text{j}}}},\;\;\;\;k = j \end{array} \right. $ | (9) |
用αkj表示干扰信号的相关系数,则
| $ {\alpha _{kj}} = \left\{ \begin{array}{l} {\rho ^2}\left( {{\delta _{kj}}} \right) + {\rho ^2}\left( {{\delta _{{\rm{kj}}}} - {T_{\rm{s}}}} \right),\;\;\;\;k \ne j\\ 1,\;\;\;\;k = j \end{array} \right. $ | (10) |
当考虑异步干扰时,用户j在m时刻接收到的信号为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_j}\left( m \right) = {\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{s}}_j}\left( m \right) + \sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {\sum\limits_{b = 1}^M {\mathit{\boldsymbol{H}}_j^b\mathit{\boldsymbol{T}}_k^b{i_{kj}}\left( m \right)} } + {n_j}\left( m \right) = }\\ {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{s}}_j}\left( m \right) + \sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_k}{i_{kj}}\left( m \right)} + {n_j}\left( m \right)} \end{array} $ | (11) |
在接收端用线性接收机
| $ {{\mathit{\boldsymbol{\hat s}}}_j} = {{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{y}}_j} $ | (12) |
在接收端可以按照迫零或最小均方误差(MMSE, minimum mean-squared error)准则[13]来设计线性接收机
| $ {{\mathit{\boldsymbol{\tilde G}}}_j} = {\left( {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}} \right)^{\rm{H}}}{\left( {{{\mathit{\boldsymbol{\tilde H}}}_j}\mathit{\boldsymbol{\tilde H}}_j^{\rm{H}} + \sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{R_{kj}}{{\mathit{\boldsymbol{\tilde H}}}_{kj}}\mathit{\boldsymbol{\tilde H}}_{kj}^{\rm{H}}} + \frac{{{N_0}}}{{M{p_0}}}{\mathit{\boldsymbol{I}}_{{N_{\rm{r}}}}}} \right)^{ - 1}} $ | (13) |
其中:
把式(7)代入式(13)可得
| $ {{\mathit{\boldsymbol{\tilde G}}}_j} = {\left( {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}} \right)^{\rm{H}}}{\left( {{{\mathit{\boldsymbol{\tilde H}}}_j}\mathit{\boldsymbol{\tilde H}}_j^{\rm{H}} + \sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\alpha _{kj}}{{\mathit{\boldsymbol{\tilde H}}}_{kj}}\mathit{\boldsymbol{\tilde H}}_{kj}^{\rm{H}}} + \frac{{{N_0}}}{{M{p_0}}}{\mathit{\boldsymbol{I}}_{{N_{\rm{r}}}}}} \right)^{ - 1}} $ | (14) |
用户j在接收端的信干噪比为
| $ \begin{array}{*{20}{c}} {{Q_j} = \frac{{{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{s}}_j}\left( m \right)} \right|}^2}}}{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_k}{i_{kj}}\left( m \right)} \right|}^2} + {{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{n}}_j}\left( m \right)} \right|}^2}} }} = }\\ {\frac{{{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}} \right|}^2}}}{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\alpha _{kj}}{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_k}} \right|}^2} + {N_0}\left\| {{{\mathit{\boldsymbol{\tilde G}}}_j}} \right\|_2^2} }}} \end{array} $ | (15) |
粒子群优化算法最早由Kennedy和Eberhart在1995年提出[14-15],通过种群个体之间的合作与竞争来搜索问题的最优解.
3.1 粒子群优化算法在维数为C的搜索空间中有S个粒子,粒子i(i=1, 2, …, S)的位置和速度分别用矢量xi=(xi1, xi2, …, xiC)T和vi=(vi1, vi2, …, viC)T来表示.粒子i所经历的最好位置用Pi=(pi1, pi2, …, piC)T来表示,即pbest.群体粒子经历的最好位置用Pg=(pg1, pg2, …, pgC)T表示,即gbest.粒子根据pbest和gbest来搜索自己的最好位置.粒子速度和位置的更新公式为[16]
| $ \mathit{\boldsymbol{v}}_{id}^{t + 1} = \omega \mathit{\boldsymbol{v}}_{id}^t + {c_1}{r_1}\left( {\mathit{\boldsymbol{p}}_{id}^t - \mathit{\boldsymbol{x}}_{id}^t} \right) + {c_2}{r_2}\left( {\mathit{\boldsymbol{p}}_{gd}^t - \mathit{\boldsymbol{x}}_{id}^t} \right) $ | (16) |
| $ \mathit{\boldsymbol{x}}_{id}^{t + 1} = \mathit{\boldsymbol{x}}_{id}^t + \mathit{\boldsymbol{v}}_{id}^t $ | (17) |
其中:t为当前迭代次数;ω为惯性权重并按照式(18)线性递减;c1和c2为学习因子;r1和r2为均匀分布在(0, 1)区间的随机数;xidt、vidt、pidt和pgdt分别代表当前迭代,第d维方向上粒子i的位置、速度、最好位置和群体粒子的最好位置.
式(16)中,第1部分表示粒子先前行为的惯性;第2部分表示认知部分,即自我信息更新;第3部分表示社会部分,即微粒间信息共享与相互合作.
惯性权重ω决定了粒子群优化算法的探索能力和开发能力,为了提高粒子寻优效率,同时避免粒子陷入局部最优,ω采用线动态权重公式[17]计算:
| $ \omega = {\omega _{{\rm{start}}}} - \frac{{{\omega _{{\rm{start}}}} - {\omega _{{\rm{end}}}}}}{{{t_{\max }}}} \times t $ | (18) |
其中:tmax为迭代最大值,ωstart和ωend分别为惯性权重的初始值和终止值,ωstart=0.9,ωend=0.4[18].
3.2 适应度函数用户j的信道矩阵通过奇异值分解后可表示为
| $ {\mathit{\boldsymbol{H}}_j} = {\mathit{\boldsymbol{U}}_j}\sum\limits_j {{\mathit{\boldsymbol{V}}_j}} $ | (19) |
其中:Uj为系统矩阵,Vj为用户信号矩阵.
假设每个用户有相同的数据流[19],即L1=L2=…=Lj=1,如果令Tj=[Vj]1来对用户j的数据流进行预编码,那么用户j将获得最大的预编码增益:
| $ {\left\| {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}} \right\|_2} = \lambda _j^{\max } $ | (20) |
其中:λjmax为矩阵Hj的最大的奇异值,[Vj]1为矩阵Vj的第1列.
如果采用奇异矢量来进行预编码,虽然能消除小区间干扰,但却会忽略预编码增益和噪声等对系统性能的影响.
如果|TjH[Vk]1|=0(j≠k), 选取Tj=[Vj]1作为用户j预编码矩阵,此时可以获得最大的预编码增益,而且可消除小区间干扰,有
| $ \sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {\frac{{{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_k}{i_{kj}}\left( m \right)} \right|}^2}}}{{{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}} \right|}^2}{N_0}}}} = 0 $ | (21) |
在用户j的接收端经过MMSE检测后,能获得最大的信干噪比为
| $ {Q_j} = \frac{{{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{s}}_j}\left( m \right)} \right|}^2}}}{{{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}} \right|}^2}{N_0}}} = \frac{{{{\left( {\lambda _j^{\max }} \right)}^2}}}{{{N_0}}} $ | (22) |
如果|TjH[Vk]1|=1(j≠k),仍选取Tj=[Vj]1作为用户j预编码矩阵,此时如果不能消除小区间干扰,将会严重影响系统性能,在用户j的接收端经过MMSE检测后,获得的信干噪比为
| $ \begin{array}{*{20}{c}} {{Q_j} = \frac{{{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{s}}_j}\left( m \right)} \right|}^2}}}{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{T}}_k}{i_{kj}}\left( m \right)} \right|}^2} + {{\left| {{{\mathit{\boldsymbol{\tilde G}}}_j}} \right|}^2}{N_0}} }} = }\\ {\frac{{{{\left( {\lambda _j^{\max }} \right)}^2}}}{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\alpha _{kj}}{{\left( {\lambda _j^{\max }} \right)}^2} + {N_0}} }} = \frac{{{{\left( {\lambda _j^{\max }} \right)}^2}/{N_0}}}{{\frac{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\alpha _{kj}}{{\left( {\lambda _j^{\max }} \right)}^2}} }}{{{N_0} + 1}}}}} \end{array} $ | (23) |
如果|TjH[Vk]1|≠0且|TjH[Vk]1|≠1 (j≠k)(这种情况在实际环境中时常存在),此时Tj≠[Vj]1,则参数ξj=TjH[Vj]1可用来衡量预编码增益,参数ρj=TjH[Vk]1可以用来衡量小区间干扰,在用户j的接收端经过MMSE检测后,获得的信干噪比为
| $ \begin{array}{*{20}{c}} {{Q_j} \approx \frac{{{{\left| {\lambda _j^{\max }\left( {\mathit{\boldsymbol{T}}_j^{\rm{H}}{{\left[ {{\mathit{\boldsymbol{V}}_j}} \right]}_1}} \right)} \right|}^2}}}{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\alpha _{kj}}{{\left| {\lambda _j^{\max }\left( {\mathit{\boldsymbol{T}}_j^{\rm{H}}{{\left[ {{\mathit{\boldsymbol{V}}_k}} \right]}_1}} \right)} \right|}^2} + {N_0}} }} = }\\ {\frac{{{{\left( {\lambda _{\rm{j}}^{\max }{\xi _{\rm{j}}}} \right)}^2}/{N_0}}}{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\alpha _{kj}}{{\left( {\lambda _{\rm{j}}^{\max }{\rho _{\rm{j}}}} \right)}^2}/\left( {{N_0} + 1} \right)} }}} \end{array} $ | (24) |
系统总速率为
| $ B = \sum\limits_{j = 1}^K {{\rm{lb}}\left( {1 + {Q_j}} \right)} $ | (25) |
因此为了获得最大的系统总速率[20],即寻找使每个用户信干噪比最大的预编码矢量为
| $ \mathit{\boldsymbol{\bar T}} = \arg \max \left( {{Q_j}\left( {\left[ {{\mathit{\boldsymbol{V}}_j}} \right],\lambda _j^{\max },{N_0}} \right)} \right),j = 1,2, \cdots ,K $ | (26) |
综上所述,适应度函数可以表示为
| $ f_{i,j}^t = \frac{{{{\left| {\lambda _j^{\max }\left[ {{{\left( {\mathit{\boldsymbol{x}}_{i,j}^t} \right)}^{\rm{H}}}{{\left[ {{\mathit{\boldsymbol{V}}_j}} \right]}_1}} \right]} \right|}^2}}}{{\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne j} \end{array}}^K {{\alpha _{kj}}{{\left| {\lambda _j^{\max }\left[ {{{\left( {\mathit{\boldsymbol{x}}_{i,j}^t} \right)}^{\rm{H}}}{{\left[ {{\mathit{\boldsymbol{V}}_k}} \right]}_1}} \right]} \right|}^2}} + \sigma _j^2}} $ | (27) |
其中σj2为高斯白噪声功率.
用粒子群优化算法搜索每个用户的最优预编码矢量,步骤如下.
1) 初始化.对每个用户j设置最大的迭代次数为I,维数为C=MNt,群体规模为S.对于粒子i速度矢量和位置矢量分别为
2) 搜索.根据初始化粒子的位置矢量和速度矢量并根据式(27)来计算各粒子当前迭代的适应值,搜索其中最大的适应值,并与上一次迭代中的适应值相比较,从而得到个体最优值pi, jt和群体最优值gi, jt.
3) 更新.根据步骤2)中得到的个体最优值pi, jt和群体最优值gi, jt,并根据式(16)和式(17)来更新粒子的速度和位置.
4) 重复步骤2)和3),达到最大迭代次数I,算法停止,则pi, jI即为粒子j的最优预编码矢量.
5) 每个粒子均按照上述步骤搜索自己的最优预编码矩阵.
4 仿真结果与分析仿真所考虑的场景如下:在多基站协作下行链路中M=3,K=3,Nt=2,Nr=2.基站分布在3个相邻小区中,每个基站服务于一个用户.基站之间的距离为500 m,用户离基站的最近距离为150 m[8].
首先,对所提算法的收敛性进行验证;其次,研究所提算法的学习因子对收敛性能的影响;最后,对所提算法与文献[8]中改进的块对角化算法进行性能比较.
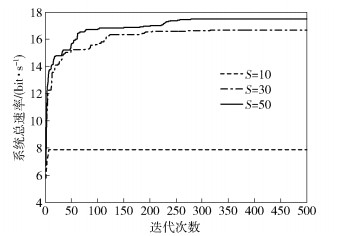
仿真了不同群体规模下所提算法的收敛性能,如图 3所示.仿真中取学习因子c1=2、c2=2.从图 3可以看出,当群体规模S=10时,由于粒子多样性较小,所以无法搜索到最优解;当群体规模S=30和S=50时,系统总速率分别可达到54.5 bit/s和55.5 bit/s.同时,还可以看出当群体规模足够寻求最优解时,增加群体规模对系统总速率影响不大,但收敛速度有一定的提高.
|
图 3 不同群体规模下所提算法的收敛性 |
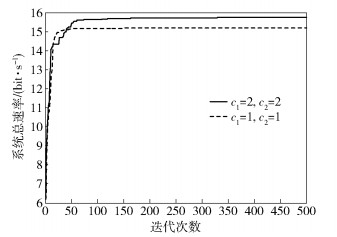
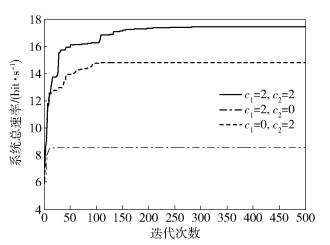
图 4和图 5所示为在群体规模S=30时,学习因子c1和c2对所提算法收敛性能的影响.从图 4可以看出,c1=1、c2=1和c1=2、c2=2两种情况下所提算法分别收敛于53.8 bit/s和55 bit/s,不同的是前者收敛速度明显优于后者.从图 5可以看出,当c1=0时,粒子没有认知能力,在粒子的相互作用下,有能力到达新的搜索空间,它的收敛速度虽然比标准版本更快, 但性能也有所下降;当c2=0时,粒子之间没有信息交流,一个规模为S的群体等价于S个单个粒子的运行,因此得到解的几率非常小.
|
图 4 c1=1、c2=1和c1=2、c2=2时,所提算法的收敛性 |
|
图 5 c1=0、c2=2和c1=2、c2=0时,所提算法的收敛性 |
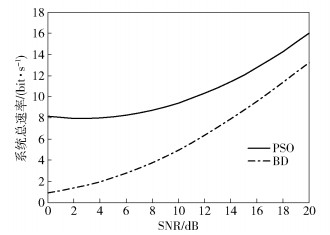
图 6所示为在群体大小S=30时,所提算法与文献[8]中改进的块对角化算法的性能比较.从图 6中可以看出,在0~20 dB的信噪比范围内,所提算法在系统总速率方面提高了2~7 bit/s,使系统性能得到提升.
|
图 6 不同算法下系统性能的比较 |
多基站协作可以大幅改善边缘小区用户的通信干扰问题,提高系统总速率.首先建立了多基站协作系统模型,并对信号的异步特性进行了详细的分析;其次以最大化每个用户的信干噪比为优化目标,提出了基于粒子群优化算法的多基站协作预编码设计;数值分析结果表明,当群体规模足够大时,所提算法收敛性较好,正确选取学习因子,可大大提升算法的性能,而且所提算法优于改进的块对角化算法.
| [1] | Trabelsi N, Chen Chung Shue, Roullet L, et al. Coordinated scheduling via frequency and power allocation optimization in cellular networks[C]//IEEE/IFIP Network Operations and Management Symposium. Istanbul: IEEE, 2016: 44-51. |
| [2] | Li Zhuoming, Liu Yuqi, Zhang Yu, et al. Hybrid coo-rdinated strategy of downlink coordinated multi-point transmission[J]. Systems Engineering and Electronics, 2015, 26(5): 916–923. doi: 10.1109/JSEE.2015.00099 |
| [3] | Heng W, Liang T, Meng C, et al. Dynamic clustering of coordinated multi-point transmission based on friends algorithm[J]. Chinese Journal of Electronics, 2015, 24(2): 414–418. doi: 10.1049/cje.2015.04.032 |
| [4] | Sun Huan, Fang Wei. Multi-user scheduling and interference alignment for cooperative multi-cell downlink transmissions[C]//IEEE Vehicular Technology Conference. Las Vegas: IEEE, 2013: 1-5. |
| [5] | Hsu C, Yeoh P L, Krongold B S. Successive convex approximation for rate maximisation in cooperative multiple input multiple-output orthogonal-frequency-division multiplexing systems[J]. The Institution of Engineering and Technology Communications, 2015, 9(14): 1721–1729. |
| [6] | Torbatian M, Najafi H, Damen M O. Asynchronous interference alignment[J]. IEEE Transactions on Wireless Communications, 2012, 11(9): 3148–3157. doi: 10.1109/TWC.2012.070912.111073 |
| [7] | Zheng Pinlian, Xie Xianzhong, Qu Gang. Suppressed inter-cell asynchronous interference by delay-tolerance SLNR precoding[C]//IEEE International Conference on Advanced Communication Technology. Gangwon-do: [s. n. ], 2010: 627-632. |
| [8] | Wang Y, Dai H, Wang T, et al. Improvedblock diagonalisation algorithm under asynchronous interference condition[J]. IET Communications, 2012, 6(3): 257–263. doi: 10.1049/iet-com.2010.0983 |
| [9] | Hassan M H, Hossain M J, Bhargava V K. Distributed beamforming and autonomous participation decision making in cooperative CR systems in presence of asynchronous interference[J]. IEEE Transactions on Wireless Communications, 2016, 15(7): 5016–5029. |
| [10] | Tang Jingming, Zhao Kun, Ni Chenquan, et al. Robust MMSE design with async-hronous interference mitigation in cooperative base stationsystems[J]. Wireless Personal Communications, 2014, 78(2): 889–903. doi: 10.1007/s11277-014-1790-3 |
| [11] |
张秀军, 肖立民, 周世东, 等. 存在传输时延差的多点协作多用户传输[J]. 东南大学学报, 2012, 6(42): 1036–1040.
Zhang Xiujun, Xiao Limin, Zhou Shidong, et al. Multi-user coordinated multi-point transmission with different delays[J]. Journal of Southeast University, 2012, 6(42): 1036–1040. |
| [12] | Zhang Hongyuan, Mehta N B, Molisch A F, et al. Asynchronous interference mitigation in cooperative base station systems[J]. IEEE Transactions on Wireless Communications, 2008, 7(1): 155–165. doi: 10.1109/TWC.2008.060193 |
| [13] | Qiao Jianyong. Two problems in the value distribution theory[J]. Acta Mathematic Sinica, 1995, 11(4): 365–371. doi: 10.1007/BF02248746 |
| [14] | Poli R, Kennedy J, Blackwell T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33–57. doi: 10.1007/s11721-007-0002-0 |
| [15] | Robinson J, Rahmat-Samii Y. Particle swarm optimization in electromagnetics[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(2): 397–407. doi: 10.1109/TAP.2004.823969 |
| [16] | Zhang Zhe, Jia Limin, Qin Yong. Modified constriction particle swarm optimization algorithm[J]. Systems Engineering and Electronics, 2015, 26(5): 1107–1113. doi: 10.1109/JSEE.2015.00120 |
| [17] | Zhan Zhihui, Zhang Jun, Li Yun, et al. Adaptive particle swarm optimization[J]. IEEE Transactions on System, Man, and Cybernetics, Part B:Cybernetics, 2009, 39(6): 1362–1381. doi: 10.1109/TSMCB.2009.2015956 |
| [18] | Hu Mengqi, Wu T F, Weir J D. An adaptive particle swarm optimization with multiple adaptive methods[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(5): 705–720. doi: 10.1109/TEVC.2012.2232931 |
| [19] | Zhang Rui, Song Rongfang. A linear pre-coding strategy based on particle swarm optimization in multicell cooperative transmission[J]. Journal of Electronics(China), 2011, 28(1): 15–21. |
| [20] | Qiao Jiangyong. On the preimages of parabolic periodic points[J]. Nonlinearity, 2000, 13(3): 813–818. doi: 10.1088/0951-7715/13/3/316 |


