为提高网络流量时间序列的中期预测精度,提出一种高斯过程回归模型补偿自回归积分滑动平均(ARIMA)模型的网络流量预测模型.首先通过Brock-Dechert-Scheinkman统计量检验方法确定网络流量时间序列包含线性特征与非线性特征;然后利用ARIMA模型对网络流量时间序列进行非平稳建模,得到符合网络流量序列线性变化规律的模型,并通过人工蜂群算法优化的高斯过程回归模型对具有非线性特性的预测误差序列进行建模与预测;最后将ARIMA模型的预测值与高斯过程回归模型的预测误差值进行相加得到最终的网络流量预测值.仿真对比实验结果表明,提出的预测方法具有更高的预测精度和更小的预测误差.
In order to improve the medium-term prediction accuracy of network traffic, a network traffic prediction method based on auto regressive integrated moving average (ARIMA) with Gaussian process regression compensation was proposed. Firstly, the linear and nonlinear characteristics of network traffic can be determined by Brock-Dechert-Scheinkman statistics. Then, ARIMA model was used for modeling the non-stationary network traffic time series. The linear model of network traffic sequence was obtained. The artificial bee colony algorithm optimized Gaussian process regression model was used as the prediction model of predictive error sequences with the nonlinear characteristic. Finally, the final prediction value was obtained by adding predictive values of ARIMA model and predictive error values of Gaussian process regression model. Simulation comparison shows that the proposed prediction method has higher prediction accuracy with the smaller prediction error.
近年来,随着信息技术的进步,网络的资源分配成为一个重要的研究课题.当网络过载或拥塞时,完善的资源分配机制能保证重要或高优先级的业务量不会发生延迟或丢弃,同时保证网络的高效运行[1].网络流量预测技术的发展与成熟使得建立一种基于流量精确预测的动态资源分配成为可能[2].网络流量预测根据应用场合不同,通常可分为短期预测、中期预测及长期预测[3-4].一般而言,长期预测通常是以比较大的颗粒度即月、日的长时间段内的历史数据为参考来分析、建模、预测未来时刻流量变化,通常更注重趋势上的准确,而不是预测值的绝对准确.短期预测则更要求实时性,要求对未来秒级甚至更小尺度的网络流量进行预测.而中期预测一般是依据几分钟至几小时的历史数据,预测出未来几分钟或几小时内网络流量的变化,同时也要求具有较高的预测准确度.相对于长期预测,中短期预测更具有挑战性和难度.
目前,网络流量的中短期预测模型包括线性模型与非线性模型.线性预测模型有自回归滑动平均(ARMA, auto regressive moving average)模型[5]、自回归积分滑动平均(ARIMA, auto regressive integrated moving average)模型[6-7]及差分自回归求和滑动平均模型[8-9]等.姜明等[10]利用以上线性模型对不同时间尺度下的网络流量预测进行了研究,仿真结果表明线性模型的预测精度有限.同时,随着现今网络模型的动态化和复杂化,网络流量特性已经偏离了相关学者认为的泊松或马尔可夫分布[11],因此线性模型无法反映网络流量表现出的新特性.而非线性预测模型的典型代表包括支持向量机[12-13]、最小二乘支持向量机[14-15](LSSVM, least square support vector machine)、人工神经网络[16-18]及灰色模型[19]等.相对于线性模型,非线性模型的预测精度有了一定程度的提高,但也存在着各自的缺陷.同时,进一步的研究也指出非线性模型对于时间序列中线性成分的预测精度有限.对于1个时间序列,因为无法确定其是否包含线性或者非线性成分,所以采用单一的线性或非线性预测模型是不适合的.最合适的方法是针对时间序列中的线性成分采用线性预测模型,而非线性成分则采用非线性预测模型.
笔者通过BDS(Brock-Dechert-Scheinkman)统计量检验方法对实际采集的中期网络流量时间序列进行分析表明,网络中期流量既含有线性成分又含有非线性成分.因此,利用ARIMA模型对原始网络中期流量进行预测,得到网络中期流量的线性趋势;然后利用具有良好非线性逼近能力的高斯过程回归模型对预测误差进行预测,并通过人工蜂群(ABC, artificial bee colony)算法对高斯过程回归模型的参数进行优化,以提高预测精度;最后将ARIMA模型的线性预测值与高斯过程回归模型的非线性预测误差值进行相加而得到最终的预测值.通过仿真对比表明,所提出的网络流量中期预测方法具有较高的预测精度.
1 网络流量的线性与非线性判定笔者利用BDS统计量检验法进行网络流量的线性/非线性判定. BDS统计量检验法是基于G-P相关积分创建的一种统计量,用于判定时间序列的非线性特征.对于长度为
| $\begin{eqnarray} \boldsymbol{x}^{m}_{t}=(x_{1τ},x_{2τ},…,x_{(m-1)τ}) \end{eqnarray}$ | (1) |
其相关积分为
| $\begin{eqnarray} C(m,n,r)=\frac{2}{M(M-1)}∑\limits_{t<s}H(r-‖\boldsymbol{x}^{m}_{t}-\boldsymbol{x}^{m}_{x}‖) \end{eqnarray}$ | (2) |
其中:
| $\begin{eqnarray} H(z)=\left\{\begin{array}{c} 0,&z≤0\\ 1,&z>1\end{array} \right. \end{eqnarray}$ | (3) |
用BDS进行检查前,需要消除原时间序列线性相关的成分,通常对原时间序列拟合自回归模型AR(
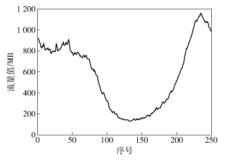
采集了250组辽宁联通169核心网络接入路由器的网络中期流量数据,数据采集尺度为10 min,数据单位为MB. 250组网络流量数据如图 1所示.
|
图 1 网络中期流量样本序列 |
令AR(
|
|
表 1 网络流量的BDS检验结果 |
标准正态分布95%的临界值为1.96,从表 1中可知,网络流量时间序列的BDS统计量检验结果远大于1.96,这就表明网络流量时间序列的残差序列不是独立同分布的时间序列,具有强烈的非线性特征.故而网络流量时间序列既含有线性又含有非线性成分.因此对残差序列需要用非线性预测模型进行预测.基于以上分析,笔者提出了一种线性与非线性模型相结合的预测方法.
2 ARIMA预测模型ARIMA模型的基本思想是通过多次差分使非平稳序列平稳化,差分次数是参数
| $\begin{eqnarray} &y_{t}=θ_{0}+φ_{1}y_{t-1}+φ_{2}y_{t-2}+…+φ_{p}y_{t-p}+\\ &ε_{t}-θ_{1}ε_{t-1}-θ_{2}ε_{t-2}-…-θ_{q}ε_{t-q} \end{eqnarray}$ | (4) |
其中:
平稳化时间序列后,首先计算原始序列的自相关函数和偏自相关函数.对于时间序列
| $\begin{eqnarray} γ_{k}=\frac{1}{N}∑\limits^{N-k}_{j=1}y_{k}y_{j+k} \end{eqnarray}$ | (5) |
自相关函数为
| $\begin{eqnarray} ρ=\frac{γ_{k}}{γ_{0}} \end{eqnarray}$ | (6) |
偏自相关函数为
| $\begin{eqnarray} &α_{11}=ρ_{1}\\ &α_{k+1,k+1}=\left(ρ_{k+1}-∑ρ_{k+1-j}α_{kj}\right)\left(1-∑\limits^{k}_{j=1}ρ_{j}α_{kj}\right)^{-1}\\ &α_{k+1,j}=α_{kj}-α_{k+1,k+1}α_{k,k-j+1} \end{eqnarray}$ | (7) |
可通过
| $\begin{eqnarray} ∑\limits^{N}_{t=1}α^{2}_{t}=∑\limits^{N}_{t=1}(θ^{-1}_{q}(Z)φ_{p}(Z)∇^{d}y_{t})^{2} \end{eqnarray}$ | (8) |
对不同的
| $\begin{eqnarray} A=-2\text{ln} L+2n \end{eqnarray}$ | (9) |
其中:
ARIMA模型的实质就是差分运算与ARMA模型的结合,即通过适当阶数的差分操作后,可实现任何非平稳时间序列的平稳,适合于线性时间序列的预测.
3 ABC算法优化的高斯过程回归高斯过程回归是近年发展起来的一种机器学习回归方法,它有着严格的统计学习理论基础,方便预测未来事物的发展.其对处理高维数、小样本、非线性等复杂问题具有很好的适应性,且泛化能力强[20].它的基本原理是:假设给定训练数据集
假定
| $\begin{eqnarray} f(\boldsymbol{x}_{i})~N[m(\boldsymbol{x}_{i}),\boldsymbol{K}],i=1,2,…,n \end{eqnarray}$ | (10) |
| $\begin{eqnarray} D:y_{i}=f(\boldsymbol{x}_{i}),i=1,2,…,n \end{eqnarray}$ | (11) |
实际目标输出
| $\begin{eqnarray} \boldsymbol{y}=f(\boldsymbol{x}_{i})+ε_{i} \end{eqnarray}$ | (12) |
其中
| $\begin{eqnarray} \left[\begin{array}{c}\boldsymbol{y}\\f_{*}\end{array}\right]~N\left(0, \left[\begin{array}{c}\boldsymbol{K}+σ^{2}_{n}\boldsymbol{I} &\boldsymbol{K}^{\text{T}}_{*}\\ \boldsymbol{K}_{*}&\boldsymbol{K}_{**}\end{array}\right]\right) \end{eqnarray}$ | (13) |
其中
| $\begin{eqnarray} &\boldsymbol{K}=\left[\begin{array}{c} k(\boldsymbol{x}_{1},\boldsymbol{x}_{1})&k(\boldsymbol{x}_{1},\boldsymbol{x}_{2})&…&k(\boldsymbol{x}_{1},\boldsymbol{x}_{n})\\ k(\boldsymbol{x}_{2},\boldsymbol{x}_{1})&k(\boldsymbol{x}_{2},\boldsymbol{x}_{2})&…&k(\boldsymbol{x}_{2},\boldsymbol{x}_{n})\\ ⋮&⋮&⋱&⋮\\ k(\boldsymbol{x}_{n},\boldsymbol{x}_{1})&k(\boldsymbol{x}_{n},\boldsymbol{x}_{2})&…&k(\boldsymbol{x}_{n},\boldsymbol{x}_{n})\end{array}\right]\\ &\boldsymbol{K}_{*}=[k(\boldsymbol{x}_{*}, \boldsymbol{x}_{1}), k(\boldsymbol{x}_{*}, \boldsymbol{x}_{2}), …, k(\boldsymbol{x}_{*}, \boldsymbol{x}_{n})]\\ &\boldsymbol{K}_{**}=k(\boldsymbol{x}_{*}, \boldsymbol{x}_{*}) \end{eqnarray}$ |
根据多元高斯分布的条件分布形式,可得出高斯过程预测方程的关键式为
| $\begin{eqnarray} f_{*}|\boldsymbol{X},\boldsymbol{y},\boldsymbol{X}_{*}~\text{GP}[m(\boldsymbol{x}_{*}),\text{cov}(f_{*})] \end{eqnarray}$ | (14) |
其中:矩阵
| $\begin{eqnarray} m(\boldsymbol{x}_{*})=\boldsymbol{K}_{*}(\boldsymbol{K}+σ^{2}_{n}\boldsymbol{I})^{-1}\boldsymbol{y} \end{eqnarray}$ | (15) |
| $\begin{eqnarray} \text{cov} (f_{*})=\boldsymbol{K}_{**}-\boldsymbol{K}_{*}(\boldsymbol{K}+σ^{2}_{n}\boldsymbol{I})^{-1}\boldsymbol{K}^{\text{T}}_{*} \end{eqnarray}$ | (16) |
高斯过程回归中协方差函数是一个满足Mercer条件的对称函数,其在有限输入集上正定,因此协方差函数等价于核函数,将式(15)改写为
| $\begin{eqnarray} m(\boldsymbol{x}_{*})=∑\limits^{n}_{i=1}\mathbf{α}_{i}\boldsymbol{K}(\boldsymbol{x}_{i},\boldsymbol{x}_{*}) \end{eqnarray}$ | (17) |
其中
| $\begin{eqnarray} \mathbf{α}_{i}=[\boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X})+δ^{2}_{n}\boldsymbol{I}]^{-1}\boldsymbol{y} \end{eqnarray}$ |
这里选择平方指数函数作为核函数,即
| $\begin{eqnarray} \boldsymbol{K}(\boldsymbol{x}_{i},\boldsymbol{x}_{j})=δ^{2}_{f}\text{exp} \left(-\frac{1}{2l^{2}}(\boldsymbol{x}_{i}-\boldsymbol{x}_{j})^{2}\right)+δ^{2}_{n}δ_{ij} \end{eqnarray}$ | (18) |
其中:
ABC算法来源于蜜蜂采蜜的行为[21]. ABC算法相对于遗传算法、差分进化算法以及粒子群优化算法具有极强的竞争力[22].基于此,采用ABC算法对高斯过程回归的超参数进行优化.
ABC算法中蜜源的位置抽象为解空间内的点,蜜源(
| $\begin{eqnarray} x_{id}=L_{d}+\text{rand}(0,1)(U_{d}-L_{d}) \end{eqnarray}$ | (19) |
搜索开始阶段,引领蜂在蜜源周围根据式(20)搜索而产生一个新的蜜源.
| $\begin{eqnarray} v_{id}=x_{id}+φ(x_{id}-x_{jd}) \end{eqnarray}$ | (20) |
其中:
| $\begin{eqnarray} p_{i}=\frac{\text{fit}_{i}}{∑\limits^{S}_{i=1} }\text{fit}_{i} \end{eqnarray}$ | (21) |
进行跟随.其中fit
| $\begin{eqnarray} &\boldsymbol{X}^{t+1}_{i}=\\ &\left\{ \begin{array}{l} L_{d}+\text{rand}(0,1)(U_{d}-L_{d}),~~尝试次数≥最大开采次数\\ \boldsymbol{X}^{t}_{i},~~尝试次数<最大开采次数 \end{array} \right. \end{eqnarray}$ | (22) |
为了获取最小的均方根误差(RMSE, root mean square error)以及和ABC算法保持一致,采用式(23)作为ABC优化高斯过程回归参数的适应度函数.
| $\begin{eqnarray} \text{fit}_{i}=\frac{1}{1+r_{i}} \end{eqnarray}$ | (23) |
其中
| $\begin{eqnarray} r_{i}=\sqrt{\frac{1}{S}∑\limits^{S}_{j=1}(y_{j}-\hat{y}_{j})^{2}} \end{eqnarray}$ | (24) |
ABC算法优化高斯模型回归预测模型的步骤如下:
步骤 1 生成训练数据样本集,同时参数初始化,包括蜜源的个数
步骤 2 为蜜源分配一只引领蜂,按照式(20)进行搜索,产生新蜜源
步骤 3 代入样本数据,根据高斯过程回归模型计算输出预测值,并根据式(23)计算适应度值,根据贪婪算法保留蜜源;
步骤 4 按式(21)计算蜜源被跟随的概率,跟随蜂搜索,根据贪婪算法保留蜜源;
步骤 5 判断蜜源
步骤 6 侦查蜂按式(22)产生新的蜜源;
步骤 7 令
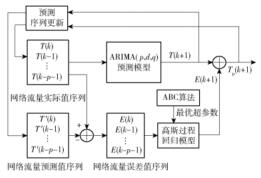
设网络流量时间序列为
|
图 2 网络流量预测模型 |
预测步骤描述如下:
步骤 1 预测模型训练,利用网络流量样本数据建立ARIMA预测模型,通过ARIMA的预测流量值与实际流量值误差建立高斯过程回归预测模型,模型中的超参数通过ABC算法得到;
步骤 2 利用
步骤 3 利用网络流量实际值与ARIMA预测值生成预测误差序列
步骤 4 将
步骤 5 更新预测序列,将
仿真数据利用上文介绍的250组辽宁联通169核心网接入路由器的网络中期流量数据(数据采集尺度为10 min),通过前200组数据进行ARIMA与高斯过程回归预测模型的建立,后50组数据用来进行预测模型精度的验证.
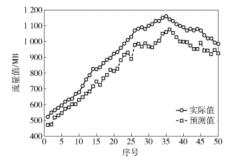
首先利用网络流量数据进行ARIMA预测模型的建立,训练完毕其模型为ARIMA(10, 1, 7),利用该模型对50组网络流量测试样本进行了预测. 图 3为ARIMA模型的网络流量预测值与实际值的对比曲线.从图中可看出ARIMA模型的网络流量预测值在趋势上可以较好地拟合实际值,预测出了网络流量时间序列中的线性特征,但是存在预测误差过大的问题,同时该预测误差是非线性的,因此需要对其预测误差进行补偿修正.
|
图 3 ARIMA模型的网络流量实际值与预测值对比 |
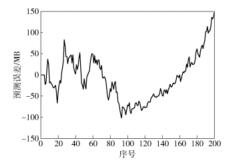
利用得到的ARIMA预测模型对200组网络流量训练样本数据进行预测,得到200组网络流量样本预测误差,其曲线如图 4所示.从图 4可见,样本预测误差时间序列具有强烈的非线性特征,因此选择高斯过程回归模型是合适的.利用预测误差序列完成高斯过程回归预测模型的建立.
|
图 4 网络流量训练样本预测误差 |
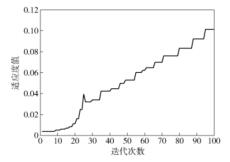
ABC算法参数设置:蜜源的个数
|
图 5 ABC算法适应度变化曲线 |
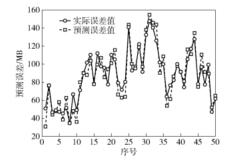
|
图 6 高斯过程回归的网络流量误差预测曲线 |

|
图 7 叠加后的网络流量实际值与预测值的对比曲线 |
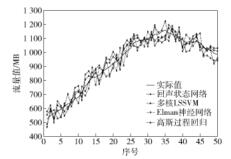
为了对比所提出预测方法的效果,图 8给出了多核LSSVM(优化后参数为
|
图 8 其他方法实际值与预测值的对比曲线 |
图 9为几种预测方法的误差分布图,从图中可观察到所提出的预测方法在预测误差上要小于其他预测方法,同时误差分布更加均匀,即预测误差随着预测步长的增长变化相对平稳,受预测步长的影响较小.

|
图 9 预测误差分布 |
为了进行预测效果的对比,引入如下4种性能指标.
1) RMSE
| $\begin{eqnarray} e_{\text{RMSE}}=\sqrt{\frac{1}{N}∑\limits^{N}_{i=1}(T_{i}-\hat{T}_{i})^{2}} \end{eqnarray}$ | (25) |
其中:
2) 平均绝对误差(MAE, mean absolute error)
| $\begin{eqnarray} e_{\text{MAE}}=\frac{1}{N}∑\limits^{N}_{i=1}|T_{i}-\hat{T}_{i}| \end{eqnarray}$ | (26) |
3) MAPE平均绝对百分误差(MAPE, mean absolute percentage error)
| $\begin{eqnarray} e_{\text{MAPE}}=\frac{1}{N}∑\limits^{N}_{i=1}\frac{|T_{i}-\hat{T}_{i}|}{T_{i}}×100 \end{eqnarray}$ | (27) |
4) 可靠性
| $\begin{eqnarray} R^{(1-a)}=\left[\frac{ξ^{(1-a)}}{N}-(1-a)\right]×100\% \end{eqnarray}$ | (28) |
其中
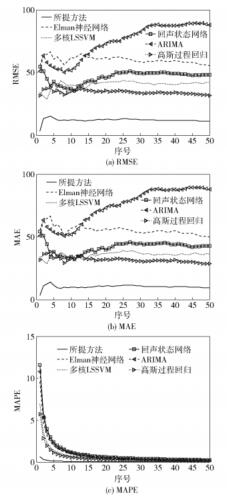
表 2给出了几种预测方法的RMSE、MAE、MAPE的性能指标对比. 图 10是这些预测方法的RMSE、MAE以及MAPE随着预测步数增加的变化曲线. 表 2与图 10中的结果同样显示,所提出的预测方法在误差的性能指标上也优于其他预测方法.
|
|
表 2 几种方法误差性能指标对比 |
|
图 10 RMSE、MAE以及MAPE变化对比曲线 |
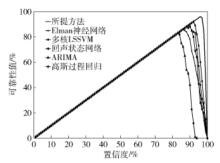
图 11为几种预测方法的可靠性值与置信度的分布图,从图中可看出所提出的方法在可靠性上要优于其他几种方法.
|
图 11 预测方法的可靠性值对比 |
提出了一种高斯过程回归补偿ARIMA的网络流量中期预测方法.利用ARIMA模型进行网络流量线性成分的预测,通过高斯过程回归模型进行具有非线性特征的网络流量预测误差的预测,同时采用ABC算法对高斯过程回归模型的参数进行优化.两种方法预测值累加得到最终的预测值,通过仿真实验对比表明所提出的方法具有很好的预测效果,对解决未来设计网络资源分配原则、拥塞控制策略、网络管理优化等问题提供了良好的基础.
致谢: 中国联合网络通信集团有限公司辽宁省分公司集团客户响应中心的顾斌工程师为笔者提供了网络流量数据,在此表示感谢!| [1] |
赵建龙, 曲桦, 赵季红, 等. 基于Morlet-SVR和ARIMA组合模型的网络流量预测[J]. 北京邮电大学学报, 2016, 39(2): 53–57.
Zhao Jianlong, Qu Hua, Zhao Jihong, et al. A comprehensive forecasting model for network traffic based on Morlet-SVR and ARIMA[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(2): 53–57. |
| [2] |
段华琼, 唐宾徽. 基于线性多尺度模型的计算机网络数据流量预测[J]. 沈阳工业大学学报, 2017, 39(3): 322–327.
Duan Huaqiong, Tang Binhui. Prediction of data flow in computer network based on linear multi-scale model[J]. Journal of Shenyang University of Technology, 2017, 39(3): 322–327. doi: 10.7688/j.issn.1000-1646.2017.03.15 |
| [3] | Tian Zhongda, Li Shujiang, Wang Yanhong, et al. A network traffic hybrid prediction model optimized by improved harmony search algorithm[J]. Neural Network World, 2015, 25(6): 669–686. doi: 10.14311/NNW |
| [4] | Qu Hua, Ma Wentao, Zhao Jihong, et al. Prediction method for network traffic based on maximum correntropy criterion[J]. China Communications, 2013, 10(1): 134–145. doi: 10.1109/CC.2013.6457536 |
| [5] | Laner M, Svoboda P, Rupp M. Parsimonious fitting of long-range dependent network traffic using ARMA models[J]. IEEE Communications Letters, 2013, 17(12): 2368–2371. doi: 10.1109/LCOMM.2013.102613.131853 |
| [6] | Yadav R K, Balakrishnan M. Comparative evaluation of ARIMA and ANFIS for modeling of wireless network traffic time series[J]. EURASIP Journal on Wireless Communications and Networking, 2014, 2014(1): 15. doi: 10.1186/1687-1499-2014-15 |
| [7] | Wang Jin. A process level network traffic prediction algorithm based on ARIMA model in smart substation[C]//2013 IEEE International Conference on Signal Processing, Communication and Computing. Kunming:IEEE Press, 2013:1-5. |
| [8] | Ren Xunyi, Yang Yu, Zhang Junfeng, et al. Parameter estimation and application of time-varying FARIMA model[J]. International Journal of Advancements in Computing Technology, 2011, 3(3): 89–94. doi: 10.4156/ijact |
| [9] | Katris C, Daskalaki S. Comparing forecasting approaches for Internet traffic[J]. Expert Systems with Applications, 2015, 42(21): 8172–8183. doi: 10.1016/j.eswa.2015.06.029 |
| [10] |
姜明, 吴春明, 张旻, 等. 网络流量预测中的时间序列模型比较研究[J]. 电子学报, 2009, 37(11): 2353–2358.
Jiang Ming, Wu Chunming, Zhang Min, et al. Research on the comparison of time series models for network traffic prediction[J]. Acta Electronica Sinica, 2009, 37(11): 2353–2358. doi: 10.3321/j.issn:0372-2112.2009.11.001 |
| [11] |
马静, 沈来信, 盛文婷. 在线开放通信网络信道分配算法优化[J]. 沈阳工业大学学报, 2017, 39(2): 193–197.
Ma Jing, Shen Laixin, Sheng Wenting. Optimization for online open communication network channel allocation algorithm[J]. Journal of Shenyang University of Technology, 2017, 39(2): 193–197. doi: 10.7688/j.issn.1000-1646.2017.02.14 |
| [12] | Liang Yonglin, Qiu Lirong. Network traffic prediction based on SVR improved by chaos theory and ant colony optimization[J]. International Journal of Future Generation Communication and Networking, 2015, 8(1): 69–78. doi: 10.14257/ijfgcn |
| [13] | Liu Xingwei, Li Hua, Chen Lei, et al. An improved forecasting algorithm for wireless network traffic[J]. IEICE Electronics Express, 2011, 8(12): 916–922. doi: 10.1587/elex.8.916 |
| [14] | Tian Zhongda, Li Shujiang. A network traffic prediction method based on IFS algorithm optimised LSSVM[J]. International Journal of Engineering Systems Modelling and Simulation, 2017, 19(4): 200–213. |
| [15] |
田中大, 高宪文, 石彤. 用于混沌时间序列预测的组合核函数最小二乘支持向量机[J]. 物理学报, 2014, 63(16): 160508.
Tian Zhongda, Gao Xianwen, Shi Tong. Combination kernel function least squares support vector machine for chaotic time series prediction[J]. Acta Physica Sinica, 2014, 63(16): 160508. doi: 10.7498/aps.63.160508 |
| [16] |
田中大, 高宪文, 李树江, 等. 遗传算法优化回声状态网络的网络流量预测[J]. 计算机研究与发展, 2015, 52(5): 1137–1145.
Tian Zhongda, Gao Xianwen, Li Shujiang, et al. Prediction method for network traffic based on genetic algorithm optimized echo state network[J]. Journal of Computer Research and Development, 2015, 52(5): 1137–1145. doi: 10.7544/issn1000-1239.2015.20131757 |
| [17] | Wang Junsong, Wang Jiukun, Zeng Maohua, et al. Prediction of Internet traffic based on Elman neural network[C]//2009 Chinese Control and Decision Conference. Guilin:IEEE Press, 2009:1248-1252. |
| [18] | Qian Feng. A extreme learning machines approach for accurate estimation of large-scale IP network traffic matrix[J]. Journal of Computational Information Systems, 2012, 8(2): 755–762. |
| [19] | Cao Jianhua, Liu Yuan, Dai Yue. Network traffic prediction based on error advanced DGM(1, 1) model[C]//International Conference on Wireless Communication Networking and Mobile Computing. Shanghai:IEEE Press, 2007:6353-6356. |
| [20] |
何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121–1129.
He Zhikun, Liu Guangbin, Zhao Xijing, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121–1129. |
| [21] | Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization:artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459–471. doi: 10.1007/s10898-007-9149-x |
| [22] | Karaboga D, Gorkemli B, Ozturk C, et al. A comprehensive survey:artificial bee colony (ABC) algorithm and applications[J]. Artificial Intelligence Review, 2014, 42(1): 21–57. doi: 10.1007/s10462-012-9328-0 |


