2. 国网河南省电力公司, 郑州 50052;
3. 中国电力科学研究院, 北京 100192
为了满足安全裕度概念下电力系统暂态稳定评估的准确率和时效性,提出了基于深度学习的堆稀疏自编码神经网络(SSAEN)预判模型.首先尝试将母线时序电压数据构成的矩阵看作蕴含暂态运行机制的模式图,然后利用SSAEN逐层级地挖掘模式图的主导特征,并通过分析SSAEN的连接权重阐述了主导特征及其演变过程.最后通过Logistic分类器识别主导特征,预判未来时刻系统的稳定性.基于IEEE39系统仿真样本进行了实验,实验结果表明,SSAEN具有较高的准确度和预测速度,可为系统暂态失稳情况提供足够的安全时间裕度.
2. State Grid Henan Electric Power Company, Zhengzhou 450052, China;
3. China Electric Power Research Institute, Beijing 100192, China
In order to satisfy the accuracy rate and timeliness performance for transition stability assessment(TSA) with a safety margin, a prediction model of stacked sparse auto-encoder network (SSAEN) is proposed based on deep learning. Firstly, the matrix obtained from the bus voltage can be treated as a pattern diagram with the TSA operating mechanism. Then, the dominant property of the pattern diagram hierarchically is mined by adopting SSAEN. And, the domination features and their evolution are described by analyzing the connection weights of the layers. Next, employing the logistic classifier can identify the dominant property. Finally, the system stability in the future time is successfully predicted. Competitive prediction speed and accuracy of the proposed SSAEN can be achieved from the simulation results in the IEEE-39-bus system, which is important to provide a sufficient safety margin when the system suffers from a temporary instability.
电力系统暂态稳定评估(TSA, transient stability assessment)问题是指电力系统在某个运行情况下突然受到大的干扰后,能否经过暂态过程达到新的稳态运行状态或者恢复到原来的状态.电力系统一旦失去稳定将会造成大范围、长时间的停电故障.
随着智能电网规模不断扩大,交直流混联输电格局的形成和电网新能源设备的融入,电力系统暂态稳定特性与运行机理的复杂度提高,电力系统安全稳定分析和调度运行控制的难度随之增大.传统的“人工+设备+经验”的生产方式已经不能满足当前电网的生产调度运行需求,且随着智能电网的深入建设,电网数据中心积累了大量数据.因此,基于数据驱动的TSA方法的研究,对提高电力系统运行的安全性、稳定性以及电力系统的长远发展都具有重要意义[1-2].
暂态稳定性的研究思路分为两类.第1类是基于数学模型的方法,主要包括数值积分法[3]、解析法[4].该类方法的共同特点是计算相对准确,不足是在线计算量大、时间长.第2类是人工智能法[5-6],该类方法是基于电网智能化发展应用的新技术,其基于历史数据演绎推理,注重在数据融合的基础上挖掘有效信息,用数据说话替代经验决策.其特点是不需要建立数学模型,计算量小,评估速度快,不足之处是不易解释物理的因果关系.
目前人工智能方法有机器学习方法,如SVM、决策树、神经网络等,其模型构建简单,但其需要手动选取特征,特征选取的重要性直接决定模型的有效性,面对具有多源时空数据的电网系统,高价值的特征选择有较大难度[7].近年来,国内外学者也开始研究深度学习(DL, deep learning)在智能电网中的应用,主要包括基于DL的输电网故障检测与定位[8]、电能质量扰动分类[9]、电网的负荷分析和预测[10]以及电网智能调度控制[11].源于人工神经网络的DL方法在特征选择上表现更为智能和高效,它能够自学习生成高阶抽象概念的复杂函数,分层地学习模式的各级特征.堆稀疏自编码器(SSAE, stacked sparse auto-encoder)是DL方法中高性能的无监督方法,再将SSAE与logistic分类器(LC, logistic classifier)连接可实现高性能的监督学习[12-13].笔者尝试将电力系统的高维时序数据看作蕴含内部运行机制的状态模式图,发挥DL挖掘图形特征的优势,为具有多源时空数据电力系统的暂态稳定性分析提供一种高效准确的技术手段.
1 理论基础 1.1 稀疏自编码器原理稀疏自编码器(SAE, sparse auto-encoder)是由编码器和解码器组成,其训练过程是尽可能使输出向量等于输入向量.由于限定隐藏层神经元的个数小于输入层神经元的个数,训练模型的核心在于完成隐藏层对输入数据的高效压缩和主导特征的获取[12].假设给定输入向量
| $\begin{eqnarray} \boldsymbol{h}(\boldsymbol{x})=\boldsymbol{W}_{2}f(\boldsymbol{W}_{1}\boldsymbol{x}+\boldsymbol{b}_{1})+\boldsymbol{b}_{2} \end{eqnarray}$ | (1) |
| $\begin{eqnarray} f(\boldsymbol{z})=1/(1+\text{exp} (\boldsymbol{z})) \end{eqnarray}$ | (2) |
描述的是非线性sigmoid激活函数.其中:
| $\begin{eqnarray} &J(\boldsymbol{W},\boldsymbol{b})=\left[\frac{1}{m}∑\limits^{m}_{l}\left(\frac{1}{2}(\boldsymbol{h}_{w,b}(\boldsymbol{x})-\boldsymbol{x})^{2}\right)\right]+\\ &λ∑\limits^{n_{l}-1}_{l=1}∑\limits^{s_{l}}_{i=1}∑\limits^{s_{l+1}}_{j=1}(W^{(l)}_{ji})^{2} \end{eqnarray}$ | (3) |
其中:
稀疏性是针对隐藏层节点而言的,即抑制大多数隐藏层神经元的激活程度,进而迫使其发挥最大潜能学习真正的主导特征.
稀疏性约束体现在代价函数的设计上,SAE的整体代价函数表达式为
| $\begin{eqnarray} J_{s}(\boldsymbol{W},\boldsymbol{b})=J(\boldsymbol{W},\boldsymbol{b})+β∑\limits^{s_{2}}_{j=2}D(ρ‖\hat{ρ}) \end{eqnarray}$ | (4) |
其中:
| $\begin{eqnarray} ∑\limits^{s_{2}}_{j=1}D(ρ‖\hat{ρ}_{j})=∑\limits^{s_{2}}_{j=1}ρ\text{lb}_{2}\left(\frac{ρ}{\hat{ρ}_{j}}\right)+(1-ρ)\text{lb} _{2}\left(\frac{1-ρ}{1-\hat{ρ}_{j}}\right) \end{eqnarray}$ | (5) |
其中:
| $\begin{eqnarray} \hat{ρ}_{j}=\frac{1}{m}∑\limits^{m}_{i=1}[a^{(2)}_{j}(x^{(i)})] \end{eqnarray}$ | (6) |
其中
电源管理单元(PMU, power management unit)是电网同步向量测量、输出及动态记录设备.对于电网状态监测而言,PMU可采集实时数据用于分析电网运行情况,是数据分析的基础.
电网运行数据具有时间性和空间性,设
笔者尝试将各母线的时序数据看作一幅蕴含运行状态的模式图,发挥深度学习模型SSAE挖掘图像特征的优势来获取该模式图的各层级主导特征.但
从样本中随机选取稳定和失稳样例,分别可视化它们的实电压时序图(见图 1).各时序图包含4 s的时间内,39条母线每隔0.005 s采样的实电压值.母线的虚电压与实电压类似.从图 1的(a)、(b)图对比分析可知,1)在暂态稳定和失稳时,对应的母线实电压的时序数据在周期性、波动规律和趋势变化等方面均存在明显的差异,但具体的主导因素不易于人工选定. 2)各母线的动态变化大致相似,即数据存在大量冗余,需要进行数据降维.

|
图 1 暂态稳定和失稳样例的模式 |
SSAE优势在于通过数据压缩的机制学习主导特征,其良好的性能可适应挖掘包含冗余数据的母线电压的主导特征,满足上述的特定需求.
2.2 无监督主导特征挖掘SSAE的构建方式为先单独训练各个SAE.每个SAE的输入层均是其上一层的隐藏层,最后,将各级隐藏层按序连接构建整体的SSAE,图 2展示了笔者设计的两层隐藏层的SSAE模型.
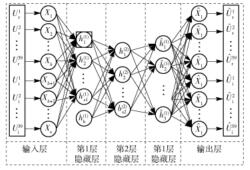
|
图 2 两层隐藏层的SSAE示意图 |
批量随机地选取无标签的样本输入SSAE网络中,以无监督的方式训练模型,模型的训练过程本质上是优化网络权重的过程.训练好的SSAE模型各层编码器的连接权重如图 3所示,解码器的权重图与编码器类似. 图 3(a)展示的是从输入层到第1层隐藏层的连接权重,图 3(b)展示的是从第1层隐藏层到第2层隐藏层的连接权重. 图 3(b)更加抽象化地描述了图 3(a),但其轮廓更加清晰,特征的展示也更加明确.它们递进地反映了SSAE模型分层地学习和抽象特征的过程.从时序电压的周期性、波动规律和趋势变化等角度观察和分析图 3(b)与图 1的(a)和(b)之间的关系可以看出,在多维空间上,图 1的(a)和(b)近似地分布在由图 3(b)构成的超平面的两侧.该超平面是SSAE模型对暂态稳定和失稳的决策边界的认知结果,反映了电网暂态运行的主导特征.从表象的层面分析,推测性地认为该平面是机器认识层面的区分暂态稳定和失稳运行模式的临界超平面.至此,SSAE在完成了母线时序冗余数据的压缩过程中,挖掘了电网暂态的运行模式的主导特征.
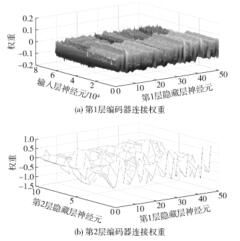
|
图 3 各层连接权重 |
SSAE可以挖掘主导特征,但其本身属于无监督模型,因此无法输出判断暂态稳定性的信息.为满足预判暂态稳定性的需求,需要在SSAE的最后一层编码器之后再接上LC,构成SSAEN,如图 4所示.利用LC学习最后一层隐藏层神经元的输出信息,并依据该特征进行监督训练,实现暂态类型的预判.
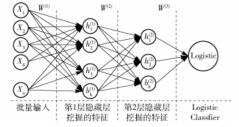
|
图 4 SSAE+LC模型示意图 |
将样本数据分为训练集和测试集,各批次的样本均从对应数据集中随机选取,每个样本采用滑动窗口的方式截取一段时序数据.使用历史数据完成模型的离线训练.首先分层训练各个SAE,完成非监督训练,提取主导特征,组合构建SSAE.然后,LC学习主导特征完成监督训练.最后,将输入层、各个SAE的隐藏层和LC按序连接,构成初始化权重等系数的SSAEN.然后进行模型微调,即将批量样本直接输入SSAEN,微调权重等系数,当模型的性能指标达标后即可完成模型的离线训练,如不达标则修改模型参数,重新训练.当模型各项性能均满足要求即可嵌入实际系统实现在线预判,测试集数据模拟在线过程,训练流程如图 5所示.
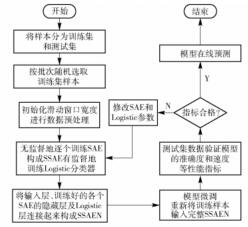
|
图 5 模型训练流程 |
仿真基于新英格兰10机39节点系统(IEEE39)标准模型,使用Matlab的PSAT模块.该标准系统有10台发电机、39条母线和46条支路,基准功率为100 MVA,基准电压为345 kV.
设计仿真类型如下,循环在系统的1~35号母线的两侧分别设置三相短路故障,故障在0.1 s时发生,在一段时间后(0.2~0.8 s的某时刻)取消故障.记录系统各母线电压
10台发电机的相对功角差的最大值
剔除计算不收敛的数据样本后,共得到2 957组样本,每组样本内容是800×78个数据点,800个时间点,78维电压值,即39条母线的实电压和虚电压,存储格式为txt,数据共计3.36 GB.其中稳定样本2 070组,失稳样本为887组.按照60%:40%的比例随机地将各组数据划分到训练集和测试集.训练集共1 774组,其中稳定样本和失稳样本分别为1 242组、532组;测试集共1 183组,其中稳定样本和失稳样本分别为828组、355组.
仿真环境:Core i5-6500,8 GB内存,GTX950显卡的台式计算机.
3.2 模型性能测试与对比分析TSA需要足够高的准确率和速度,模型性能测试主要针对以上两指标.本实验中,SSAEN模型通过前
受试者工作特征曲线(ROC, receiver operating characteristic)是反映分类敏感性和特异性的连续变量的综合评价指标.它独立于分类阈值,且可以排除类别不平衡的干扰,因此,被广泛应用于评价二分类器性能的优劣. ROC曲线所覆盖的区域面积(AUC, area under roc curve)反映模型的准确性. AUC在0.5~0.7时有较低准确性,AUC在0.7~0.9时有一定准确性,AUC在0.9以上时有较高准确性. AUC越大,表明分类器分类效果越好.
图 6展示了不同
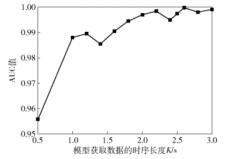
|
图 6 不同 |
从图 7中可以看出,随着
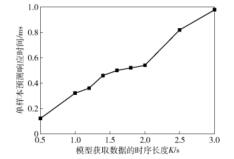
|
图 7 不同 |
图 8所示为模型在

|
图 8 损失函数收敛情况 |
笔者分别选取MLP、Logistic、SVM与SSAEN模型做性能对比分析测试.为保证实验的一般性,分别选取
表 1仅列举各模型的核心参数,MLP的隐藏层个数
|
|
表 1 模型性能对比表 |
从表 1中各性能指标对比分析可知,各模型在获取相同信息量数据的情况下,SSAEN模型的正确率和AUC值均超过MLP、Logistic、SVM模型,表明该模型自学习的主导特征是有效的. SSAEN模型的在线预测速度在毫秒级,预测速度基本增加,呈线性增长趋势,符合实际要求.
4 结束语笔者根据智能电网的真实情况,从人工智能方法的角度,提出基于深度学习方法的层级架构SSAEN模型.该模型分层级地自学习电力系统暂态运行状态的主导特征,并依据特征预判未来时刻的系统稳定性.笔者通过实验验证了设计模型的正确性和有效性,得到如下结论:
1) 应用于智能电网运行的多源时空复杂数据,SSAEN自学习特征的过程较传统ML方法的过程更加智能与高效.
2) 将高维时序母线电压和相角数据看作蕴含暂态运行机制的模式图,SSAEN挖掘模式图的主导特征来预判系统暂态稳定性的设计思路具有合理与实用性.
3) SSAEN各层连接权重的可视化清晰地展现了电网时序数据的周期性、波动规律和趋势变化等主导特征形成的临界分类超平面,反映了模型提取主导特征及数据压缩的过程,在一定程度上融入了物理机理与因果关系.
随着人工智能技术的发展,深度学习方法将在电力系统智能化进程中扮演更加重要的角色.
| [1] |
张东霞, 苗新, 刘丽平, 等. 智能电网大数据技术发展研究[J]. 中国电机工程学报, 2015, 35(1): 2–11.
Zhang Dongxia, Miao Xin, Liu Liping, et al. Research on development strategy for smart grid big data[J]. Proceedings of the CSEE, 2015, 35(1): 2–11. |
| [2] |
薛禹胜, 赖业宁. 大能源思维与大数据思维的融合(一)大数据与电力大数据[J]. 电力系统自动化, 2016, 40(1): 1–8.
Xue Yusheng, Lai Yening. Integration of macro energy thinking and big data thinking part one applications and explorations[J]. Automation of Electric Power Systems, 2016, 40(1): 1–8. doi: 10.7500/AEPS20151208005 |
| [3] |
武同心, 吕晓祥, 王建全. Duhamel数值积分算法在电力系统暂态稳定分析中的应用[J]. 机电工程, 2013, 30(6): 741–745.
Wu Tongxin, Lü Xiaoxiang, Wang Jianquan. Application of duhamel integrals in power system transient stability analysis[J]. Mechanical & Electrical Engineering Magazine, 2013, 30(6): 741–745. |
| [4] |
刘怀东, 张江红, 刘沛龙, 等. 基于改进解析法的小范围动态安全域搜索方法[J]. 电力自动化设备, 2012, 32(2): 29–33.
Liu Huaidong, Zhang Jianghong, Liu Peilong, et al. Small-range search of DSR based on improved analytical method[J]. Electric Power Automation Equipment, 2012, 32(2): 29–33. |
| [5] |
戴远航, 陈磊, 张玮灵, 等. 基于多支持向量机综合的电力系统暂态稳定评估[J]. 中国电机工程学报, 2016, 36(5): 1173–1180.
Dai Yuanhang, Chen Lei, Zhang Weiling, et al. Power system transient stability assessment based on multi-support vector machines[J]. Proceedings of the CSEE, 2016, 36(5): 1173–1180. |
| [6] | Ji L, Wu J, Zhou Y, et al. Using trajectory clusters to define the most relevant features for transient stability prediction based on machine learning method[J]. Energies, 2016, 9(11): 898. doi: 10.3390/en9110898 |
| [7] | Wang S, Lu S, Zhou N, et al. Dynamic-feature extraction, attribution, and reconstruction (DEAR) method for power system model reduction[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2049–2059. doi: 10.1109/TPWRS.2014.2301032 |
| [8] | He Y, Mendis G J, Wei J. Real-time detection of false data injection attacks in smart grid:a deep learning-based intelligent mechanism[J]. IEEE Transactions on Smart Grid, 2017, 8(5): 2505–2516. doi: 10.1109/TSG.2017.2703842 |
| [9] | Ma J, Zhang J, Xiao L, et al. Classification of power quality disturbances via deep learning[J]. IETE Technical Review, 2016: 1–8. |
| [10] | Jetcheva J G, Majidpour M, Chen W P. Neural network model ensembles for building-level electricity load forecasts[J]. Energy & Buildings, 2014(84): 214–223. |
| [11] | Kuznetsova E, Li Y F, Ruiz C, et al. Reinforcement learning for microgrid energy management[J]. Energy, 2013, 59(59): 133–146. |
| [12] | Xu J, Xiang L, Liu Q, et al. Stacked sparse autoencoder (SSAE) for nuclei detection on breast cancer histopathology images[J]. IEEE Transactions on Medical Imaging, 2016, 35(1): 119. doi: 10.1109/TMI.2015.2458702 |
| [13] | Othman E, Bazi Y, Alajlan N, et al. Using convolutional features and a sparse autoencoder for land-use scene classification[J]. International Journal of Remote Sensing, 2016, 37(10): 2149–2167. doi: 10.1080/01431161.2016.1171928 |


