针对多媒体业务普及导致网络业务量突发性增强的问题,利用随机几何建模,研究了异构蜂窝网络中基于业务量突发性的最优基站密度.基于业务量突发性提出业务覆盖率定义,推导出异构蜂窝网络中业务覆盖率与基站密度之间的关系.以业务覆盖率为限制条件,构建目标为最小化基站密度的优化问题.利用二分搜索法获得最优基站密度,并推导出最优基站密度的上、下限.通过仿真结果验证了理论推导的准确性,证实了业务量突发性对最优基站密度的影响.
To cope with the bursty traffic caused by popularity of multimedia services, the optimal base station density in heterogeneous networks by taking into account the burst characteristics of the traffic was analyzed using stochastic geometry approach. Based on bursty traffic, the traffic coverage probability of the heterogeneous network was defined and its relation with the base station density was specifically derived. An optimization problem with the aim of minimizing the base station density was formulated under the constraint of traffic coverage probability. Using binary search algorithm, the optimal base station density and the bounds (both upper and lower bound) for simplified analysis are obtained. Simulation confirms the accuracy of theoretical analysis and verifies the impact of the burst characteristics on the optimal base station density.
在无线数据流量爆炸式增长的影响下,未来蜂窝网络为异构场景.目前异构蜂窝网络基站部署的研究已非常普遍[1-3]. Cosku等[1]提出了一种贪婪微基站部署方案,在宏基站覆盖范围内放置微基站扩大网络容量. Yunas等[2]研究了密集异构蜂窝网络中不同类型基站部署场景下系统的频谱效率和能量效率. Hu等[3]分析微基站部署对中断率的影响,提出了一种快速收敛的启发式算法计算最优微基站位置.这类研究针对具体场景建立优化问题,利用仿真分析获得基站部署方案,无法提供普遍适用的理论依据.
与之对应,随机几何理论能够采用统一的数学公式,利用空间泊松点过程建立易处理的模型,有效分析覆盖率、网络容量、能量效率等各项性能,为基站部署提供理论支撑. Peng等[4]通过联合优化基站密度和发射功率,在满足网络覆盖率限制条件下,最小化单位面积功率消耗. Feng等[5]研究了密集部署异构蜂窝网中网络容量与微基站密度的关系,选择最优微基站密度,解决最大化网络容量问题.
基站部署中,业务量分布是普遍考虑的因素之一.由于昼夜更替、用户移动和数据业务的突发特性,业务量分布在时间、空间和用户间存在不平衡.根据业务量空间分布设计的基站部署方案能有效降低功率消耗和成本支出,提高网络运营商的经济效益.相应的研究主要有2种,一种是基于业务量密度分布进行基站部署. Lee等[6]将服务区域划分为相同面积的网格,利用对数正态随机场生成网格业务量密度分布,指导基站部署.另一种假设用户的业务量要求相同,则业务量分布简化为用户的空间分布,极大地降低了部署的复杂度[7].这种部署方法没有体现实际网络场景中用户业务量需求的差异性.
目前移动多媒体应用广泛普及,网络业务量突发性增强[8].由于用户的业务量突发性相互独立,用户间业务量分布存在较大的差异性.基于用户业务量分布的基站部署,一方面能够满足不同用户的业务量需求,保证服务质量要求;另一方面使得基站的密度适应用户的业务量分布,能够有效应对业务量的突发特性,在保证网络覆盖率要求的同时降低成本开销,为实际基站部署提供可靠的理论依据.
笔者针对业务量突发性研究异构蜂窝网络中最优基站密度.基于满足突发性的用户业务量分布,提出异构蜂窝网络业务覆盖率的定义.利用随机几何建模,推导业务覆盖率的表达式及使用平均负载的简化式,分析业务覆盖率与基站密度的关系.构建以业务覆盖率为限制条件,最小化基站密度的优化问题,通过二分搜索法获得最优基站密度.为便于分析业务量突发性对最优基站密度的影响,近似计算最优基站密度的上、下限.
1 系统模型 1.1 异构蜂窝网络模型采用下行异构蜂窝网络场景.网络共K层,
信道建模时,考虑路径损耗和瑞利衰落.典型用户与k层xk
| $ x_k^ * = \arg \mathop {\max }\limits_{x \in {\mathit{\Phi }_k}} {P_k}{h_x}{\left\| x \right\|^{ - \alpha }} $ |
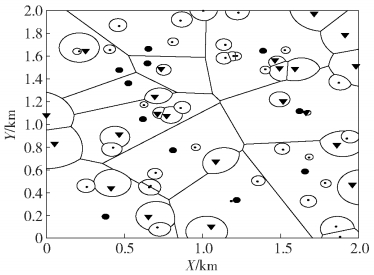
接入基站从K个候选基站中选取.由于不同层基站的发射功率不同,基站的覆盖范围构成加权泊松泰森多边形,如图 1所示.定义层接入标记Sk∈{0, 1},Sk=1(x*=xk*)=1(x*∈Φk). Sk=1表示典型用户的接入基站属于k层,反之表示不属于k层.
|
图 1 异构蜂窝网络的加权泰森多边形 |
假设典型用户接入k层,x*=xk*,定义xk*为标记基站.设置频率复用因子为1,用户信干噪比(SINR, signal to interference plus noise ratio)为
| $ R\left( {x_k^ * } \right) = \frac{{{P_k}{h_{x_k^ * }}{{\left\| {x_k^ * } \right\|}^{ - \alpha }}}}{{\sum\limits_{k = 1}^K {\sum\limits_{y \in {\mathit{\Phi }_i}\backslash x_k^ * } {{P_i}{h_y}{{\left\| y \right\|}^{ - \alpha }} + {\sigma ^2}} } }} $ | (1) |
其中σ2为热噪声.
系统带宽为W.标记基站将频谱资源平均分配给其覆盖下的所有用户,即基站负载,表示为Nk.利用香农公式,典型用户的下行可达速率计算为
| $ {R_k} = \frac{W}{{{N_k}}}{\rm{lb}}\left( {1 + R\left( {x_k^ * } \right)} \right) $ | (2) |
大量实验表明,无线网络业务量具备突发性,并且突发没有明确长度,在不同时间尺度下表现相同的突发特性,这种突发性不随时间尺度的变化而变化的特性称作自相似性. Xiang等[8]证明微观上具有重尾特性的分布能够在宏观上产生自相似性.
采用典型满足自相似特性的业务量分布模型:具有无穷大方差的帕累托分布.在这个模型中,假设用户业务量L服从独立同分布的帕累托分布.业务量L的概率密度函数表示为
| $ {f_L}\left( l \right) = \frac{{\theta l_{\min }^\theta }}{{{l^{\theta + 1}}}},\;\;\;l \ge {l_{\min }} \ge 0 $ | (3) |
其中:θ∈(1, 2]为形状参数,反映了业务量分布的重尾程度(θ越小, 业务量的突发性越强;θ趋近于2,业务量分布接近均匀分布);lmin为最小业务量,业务量的均值可以利用E(L)=
下面定义业务覆盖率.通过限制业务覆盖率大于固定阈值,构建最小化基站密度的优化问题.利用二分搜索法求解最优基站密度及其上、下限.
定义1 (业务覆盖率) 异构蜂窝网络中,假设用户的业务量分布服从帕累托分布,业务覆盖率定义为典型用户从接入基站接收的下行可达速率大于用户业务量的概率,即Pl=
K层异构蜂窝网络的业务覆盖率表示为
| $ \begin{array}{*{20}{c}} {\mathbb{P}{{\left( {r > L} \right)}^{\left( {\rm{a}} \right)}} = } \\ {\sum\limits_{l \in L} {\sum\limits_{k = 1}^K {{\mathbb{E}_{{N_k}}}\mathbb{P}\left( {\frac{W}{{{N_k}}}{\rm{lb}}\left( {1 + R} \right) > l\left| {{S_k} = 1} \right.} \right)} } \times } \\ {\mathbb{P}\left( {{S_k} = 1} \right)\mathbb{P}\left( {L = l} \right) = } \\ {\sum\limits_{l \in L} {\sum\limits_{k = 1}^K {\sum\limits_{n = 0}^\infty {\underbrace {\mathbb{P}\left( {R > {2^{n\frac{1}{W}}} - 1\left| {{S_k} = 1} \right.} \right)}_{层覆盖率}} } } \times } \\ {\underbrace {\mathbb{P}\left( {{N_k} = n} \right)}_{基站负载}\underbrace {\mathbb{P}\left( {{S_k} = 1} \right)}_{接入概率}\underbrace {\mathbb{P}\left( {L = l} \right)}_{业务量分布}} \end{array} $ | (4) |
其中:(a)表示全概率公式;
引理1 K层异构蜂窝网络中,典型用户接入k层的概率表示为[10]
| $ {\mathscr{S}_k} = \frac{{{\lambda _k}P_k^{2/\alpha }}}{{\sum\limits_{j = 1}^K {{\lambda _j}P_j^{2/\alpha }} }} $ | (5) |
引理1表明用户接入k层的概率由各层基站密度及发射功率决定.
引理2 K层异构蜂窝网络中,T表示覆盖率阈值,典型用户接入k层时的网络覆盖率表示为[10]
| $ {\mathscr{C}_k} = \frac{{2{\rm{ \mathsf{ π} }}{\lambda _k}}}{{{\mathscr{S}_k}}}\int_0^\infty {x\exp \left\{ { - \frac{T}{{{\gamma _{{\rm{SNR}}}}}} - {\rm{ \mathsf{ π} }}\sum\limits_{j = 1}^K {{D_j}{x^{2/\alpha }}} } \right\}{\rm{d}}x} $ | (6) |
其中:
蜂窝网络中,干扰相对热噪声占主导地位.当热噪声为0时,各层的网络覆盖率相同,表示为
| $ {\mathscr{C}_k} = \frac{1}{{1 + Z\left( {T,\alpha ,1} \right)}} $ | (7) |
引理3 K层异构蜂窝网络中,k层标记基站负载的概率质量函数表示为[10]
| $ \begin{array}{*{20}{c}} {P\left( {{N_k} = n + 1} \right) = }\\ {\frac{{{{3.5}^{3.5}}}}{{n!}}\frac{{\Gamma \left( {n + 4.5} \right)}}{{\Gamma \left( {3.5} \right)}}{{\left( {\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)}^n}{{\left( {3.5 + \frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)}^{ - \left( {n + 4.5} \right)}}} \end{array} $ | (8) |
其中:Γ(x)=
综上,将式(3)、式(5)、式(7)、式(8)代入式(4)可得到业务覆盖率的具体表达式.
定理1 K层异构蜂窝网络中,业务覆盖率为
| $ \begin{array}{*{20}{c}} {{\mathscr{P}_l} = \int_{{l_{\min }}}^\infty {\sum\limits_{k = 1}^K {\sum\limits_{n = 0}^\infty {\frac{{{\lambda _k}P_k^{2/\alpha }}}{{\sum\limits_{j = 1}^K {\lambda _j^{2/\alpha }{P_j}} }}\left( {1 + } \right.} } } }\\ {{{\left. {Z\left( {{2^{\left( {n + 1} \right)\frac{c}{W}}} - 1,\alpha ,1} \right)} \right)}^{ - 1}} \times }\\ {\frac{{{{3.5}^{3.5}}}}{{n!}}\frac{{\Gamma \left( {n + 4.5} \right)}}{{\Gamma \left( {3.5} \right)}}{{\left( {\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)}^n} \times }\\ {{{\left( {3.5 + \frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)}^{ - \left( {n + 4.5} \right)}}\frac{{\theta l_{\min }^\theta }}{{{l^{\theta + 1}}}}{\rm{d}}l} \end{array} $ | (9) |
定理1中,异构蜂窝网络的业务覆盖率表达式包括2个嵌入式广义积分、一个无穷序列求和以及伽马函数、高斯超几何函数的查表运算.计算复杂度高,运算量大.为减少运算,设置标记基站负载Nk等于平均负载,业务覆盖率可以进一步化简.
推论1 K层异构蜂窝网络中,基于平均负载的业务覆盖率表示为
| $ \begin{array}{*{20}{c}} {{{\bar {\mathscr{P}}}_l} = \int_{{l_{\min }}}^\infty {\sum\limits_{k = 1}^K {\frac{{{\lambda _k}P_k^{2/\alpha }}}{{\sum\limits_{j = 1}^K {{\lambda _j}P_j^{2/\alpha }} }}\left( {1 + } \right.} } }\\ {{{\left. {Z\left( {{2^{\left( {1 + 1.28\frac{{{\lambda _k}P_k^{2/\alpha }}}{{\sum\limits_{j = 1}^K {{\lambda _j}P_j^{2/\alpha }} }}} \right)\frac{l}{W}}} - 1,\alpha ,1} \right)} \right)}^{ - 1}}\frac{{\theta l_{\min }^\theta }}{{{l^{\theta + 1}}}}{\rm{d}}l} \end{array} $ | (10) |
证明 Singh等[10]证明k层标记基站的平均负载为
| $ {{\bar N}_k} = E\left( {{N_k}} \right) = 1 + 1.28\frac{{{\lambda _k}{\mathscr{C}_k}}}{{{\lambda _k}}} $ | (11) |
在式(9)中使用平均负载Nk代替Nk,消除了n的无穷级数求和,可以得到式(10),推论1得证.
笔者基于K层异构蜂窝网络的业务覆盖率构建最优基站密度问题,如式(12)所示.假设η为业务覆盖率阈值,最优基站密度问题表述为:已知K-1层基站密度,求满足业务覆盖率限制条件的最小K层基站密度.
| $ \begin{array}{l} \min {\lambda _k}\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\int_{{l_{\min }}}^\infty {\sum\limits_{k = 1}^K {\frac{{{\lambda _k}P_k^{2/\alpha }}}{{\sum\limits_{j = 1}^K {{\lambda _j}P_j^{2/\alpha }} }}\left( {1 + } \right.} } \\ \;\;\;\;\;\;\;{\left. {Z\left( {{2^{\left( {1 + 1.28\frac{{{\lambda _k}P_k^{2/\alpha }}}{{\sum\limits_{j = 1}^K {{\lambda _j}P_j^{2/\alpha }} }}} \right)\frac{l}{W}}} - 1,\alpha ,1} \right)} \right)^{ - 1}}\frac{{\theta l_{\min }^\theta }}{{{l^{\theta + 1}}}}{\rm{d}}l \ge \eta \end{array} $ | (12) |
对优化问题式(12)中限制条件的左边表达式
推导上、下限时,主要是通过对k层网络覆盖率
定理2 优化问题式(12)的最优K层基站密度具有上限值λKub,λKub满足:
| $ \begin{array}{*{20}{c}} {\sum\limits_{k = 1}^K {\mathscr{S}_k^{{\rm{ub}}}\frac{{\theta l_{\min }^\theta \left( {\alpha - 2} \right){{\ln }^\theta }2}}{{2{W^\theta }}}{{\left( {\bar N_k^{{\rm{ub}}}} \right)}^\theta }} \sum\limits_{m = 0}^\infty {{{\left( {\frac{{4 - \alpha }}{2}} \right)}^m}} \times }\\ {{{\left( {m + 1} \right)}^\theta }\Gamma \left( { - \theta ,\frac{{{l_{\min }}\ln 2\left( {m + 1} \right)\bar N_k^{{\rm{ub}}}}}{W}} \right) = \eta } \end{array} $ | (13) |
其中
| $ \begin{array}{*{20}{c}} {\mathscr{S}_k^{{\rm{ub}}} = \frac{{{\lambda _k}P_k^{2/\alpha }}}{{\sum\limits_{i = 1}^{K - 1} {{\lambda _i}P_i^{2/\alpha } + \lambda _K^{{\rm{ub}}}P_K^{2/\alpha }} }},\bar N_k^{{\rm{ub}}} = 1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k^{{\rm{ub}}}}}}{{{\lambda _k}}},}\\ {{\lambda _k} = \left\{ \begin{array}{l} {\lambda _k}\;\;\;\;\;\;k = 1,2, \cdots ,K - 1\\ \lambda _K^{{\rm{ub}}}\;\;\;\;k = K \end{array} \right.,\Gamma \left( {\nu ,x} \right) = \int_x^\infty {{t^{\nu - 1}}{{\rm{e}}^{ - t}}{\rm{d}}t} } \end{array} $ |
是不完全伽马函数.
证明见附件A.
推导下限时,利用文献[11]的结论:覆盖率
定理3 优化问题式(12)的最优K层基站密度具有下限值λKlb,λKlb满足:
| $ \begin{array}{l} \sum\limits_{k = 1}^K {\mathscr{S}_k^{{\rm{lb}}}\frac{{\theta l_{\min }^\theta {{\ln }^\theta }2}}{{2{W^\theta }}}{{\left( {\bar N_k^{{\rm{lb}}}} \right)}^\theta }} \sum\limits_{m = 0}^\infty {{2^{ - m}}\left( {\frac{3}{4}m + } \right.} \\ {\left. {\frac{1}{4}} \right)^\theta }\Gamma \left( { - \theta ,\frac{{{l_{\min }}\ln 2\left( {m + 1} \right)\bar N_k^{{\rm{lb}}}}}{W}} \right) = \eta \end{array} $ | (14) |
其中:
| $ \bar N_k^{{\rm{lb}}} = 1 + 1.28\frac{{{\lambda _u}\mathscr{S}_k^{{\rm{lb}}}}}{{{\lambda _k}}},{\lambda _k} = \left\{ \begin{array}{l} {\lambda _k}\;\;\;\;\;k = 1,2, \cdots ,K - 1\\ \lambda _K^{{\rm{lb}}}\;\;\;\;k = K \end{array} \right.. $ |
证明见附件B.
上述定理说明,异构蜂窝网络中,最优K层基站密度不仅与阈值η、路径损耗因子α有关,也取决于用户业务量分布的形状参数θ、最小业务量lmin.这意味着在进行实际基站部署时,不仅需要保证整体网络的覆盖率,同时也要考虑用户的业务量分布.
3 仿真分析采用蒙特卡洛仿真验证理论分析.考虑室外双层异构蜂窝网络场景,覆盖范围是半径为200 m的圆形区域.用户和宏基站、微基站分布服从相互独立的泊松点过程(PPP, poisson point process)密度分别为λu=0.01 m-2、λ1=0.003λu、λ2. P1、P2分别为46 dBm、30 dBm,W为10 MHz,α=4.各项仿真结果均通过1万次仿真取得.
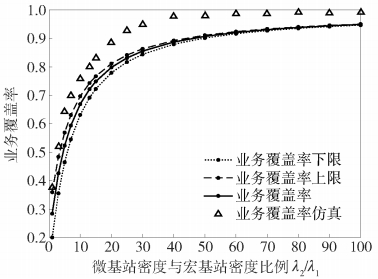
图 2显示了微基站密度对业务覆盖率的影响,lmin=50 kbit/s,θ=1.5.业务覆盖率随着微基站密度的增加而逐渐增大,最终趋于稳定.原因是增加微基站密度能将部分用户从宏基站转移到微基站,降低基站负载,使得每个用户分配的频谱资源增加, 提高下行速率.随着微基站密度继续上升,层内干扰和层间干扰也快速增强,限制了业务覆盖率的提升.图 2中业务覆盖率的上限与下限曲线均无限接近原始曲线,证明利用定理2、3获得的最优微基站密度的上、下限是紧界,近似合理.
|
图 2 业务覆盖率与微基站密度的关系 |
图 2中,理论曲线和仿真曲线呈现相同趋势,但具体数值存在差异. λ2/λ1≤15时吻合较好,当λ2/λ1>15时,两者出现差距,差距由式(7)引入.文献[10]显示,当T < 1时,k层网络覆盖率的理论结果与仿真结果存在差异.双层异构蜂窝网络业务覆盖率公式中,宏(微)基站层的阈值
图 3、图 4示出了业务量分布参数重尾系数θ、最小业务量lmin对最优微基站密度的影响. 图 3中,设置lmin=50 kbit/s,η=0.7.最优微基站密度随着θ的降低而增加.当θ接近1时,用户业务量的突发性增强,意味着对单个用户而言,大业务量出现的可能性变大,导致网络中大业务量要求的用户比例上升,因此需要提升微基站密度应对业务量的突发性,满足业务覆盖率要求.

|
图 3 最优微基站密度与重尾系数的关系 |
|
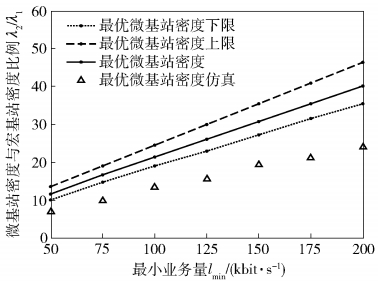
图 4 最优微基站密度与最小业务量的关系 |
图 4中,设置θ=1.5,η=0.7.随着lmin增加,每个用户的业务量要求均增加,导致网络的总体业务量大幅度上升,因此需要部署更多微基站保证业务覆盖率的要求,最优微基站密度增加.在图 3、图 4中,当重尾系数较小或者最小业务量较大时,基站阈值T < 1的概率增加,理论值与仿真数值间差距变大.此外,随着
研究了基于业务量突发性的异构蜂窝网络最优基站密度.针对突发性用户业务量分布,利用随机几何建模,分析业务覆盖率.以业务覆盖率为限制条件,构建目标为最小化基站密度的优化问题,求得最优基站密度及其上、下限.仿真分析了业务量突发性对最优基站密度的影响,验证了理论推导的准确性.
附件A
对k层网络覆盖率表达式(7)进行化简:
| $ \begin{array}{l} {\mathscr{C}_k} = \frac{1}{{1 + {T^{2/\alpha }}\int_{{T^{ - 2/\alpha }}}^\infty {\frac{1}{{1 + {x^{\alpha /2}}}}{\rm{d}}x} }} > \\ \frac{1}{{1 + {T^{2/\alpha }}\int_{{T^{ - 2/\alpha }}}^\infty {{x^{ - \alpha /2}}{\rm{d}}x} }} = \frac{1}{{1 + \frac{2}{{\alpha - 2}}T}} \end{array} $ | (15) |
使用标记基站的平均负载Nk近似Nk,将
| $ \begin{array}{*{20}{c}} {{\mathscr{C}_k} = {{\frac{1}{{1 + \frac{2}{{\alpha - 2}}\left( {{2^{\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{W}}} - 1} \right)}}}^{\left( {\rm{a}} \right)}} = }\\ {\frac{{\alpha - 2}}{2}{2^{ - \left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{W}}}\sum\limits_{m = 0}^\infty {{{\left( {\frac{{4 - \alpha }}{2}{2^{ - \left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\left( {m + 1} \right)\frac{l}{W}}}} \right)}^m}} = }\\ {\frac{{\alpha - 2}}{2}\sum\limits_{m = 0}^\infty {{{\left( {\frac{{4 - \alpha }}{2}} \right)}^m}} {2^{ - \left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\left( {m + 1} \right)\frac{l}{W}}}} \end{array} $ | (16) |
由于α∈(2, 4],故
| $ \begin{array}{*{20}{c}} {{{\bar {\mathscr{P}}}_l} \ge \int_{{l_{\min }}}^\infty {\sum\limits_{k = 1}^K {{\mathscr{S}_k}\frac{{\alpha - 2}}{2}} \sum\limits_{m = 0}^\infty {{{\left( {\frac{{4 - \alpha }}{2}} \right)}^m}} } \times }\\ {{2^{ - \left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\left( {m + 1} \right)\frac{l}{W}}}\frac{{\theta l_{\min }^\theta }}{{{l^{\theta + 1}}}}{\rm{d}}l = }\\ {\sum\limits_{k = 1}^K {{\mathscr{S}_k}\frac{{\alpha - 2}}{2}} \sum\limits_{m = 0}^\infty {{{\left( {\frac{{4 - \alpha }}{2}} \right)}^m}} \times }\\ {\int_{{l_{\min }}}^\infty {{{\rm{e}}^{ - \ln 2\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\left( {m + 1} \right)\frac{l}{W}}}\frac{{\theta l_{\min }^\theta }}{{{l^{\theta + 1}}}}{\rm{d}}l} } \end{array} $ |
令
| $ \begin{array}{*{20}{c}} {l = \frac{{Wt}}{{\ln 2\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\left( {m + 1} \right)}} = }\\ {\sum\limits_{k = 1}^K {{\mathscr{S}_k}\frac{{\theta l_{\min }^\theta \left( {\alpha - 2} \right){{\ln }^\theta }2}}{{2{W^\theta }}}{{\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)}^\theta }} \times }\\ {\sum\limits_{m = 0}^\infty {{{\left( {\frac{{4 - \alpha }}{2}} \right)}^m}{{\left( {m + 1} \right)}^\theta }} \times }\\ {\Gamma \left( { - \theta ,\frac{{{l_{\min }}\ln 2\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\left( {m + 1} \right)}}{W}} \right)} \end{array} $ | (17) |
其中Γ(x, a)=
附件B
文献[11]的定理3引理证明,k层网络覆盖率式(7)是关于路径损耗因子α的递增函数.当α∈(2, 4]时,令α=4,覆盖率取得最大值,即
| $ \begin{array}{*{20}{c}} {{\mathscr{C}_k} \le {\mathscr{C}_k}\left( {\alpha = 4} \right) = }\\ {{{\frac{1}{{1 + \sqrt T \arcsin \left( {\sqrt {\frac{T}{{1 + T}}} } \right)}}}^{\left( {\rm{b}} \right)}} \le \frac{{\sqrt {1 + T} }}{{\sqrt {1 + T} + T}}} \end{array} $ | (18) |
不等式(b)成立是由于x∈[0, 1],arcsin(x)≥x.将T=
| $ \begin{array}{*{20}{c}} {{\mathscr{C}_k} \le {{\frac{{{2^{\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{W}}}}}{{{2^{\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{{2W}}}} + {2^{\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{W}}} - 1}}}^{\left( c \right)}} \le }\\ {\frac{{{2^{\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{W}}}}}{{2 \times {2^{\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{{3l}}{{4W}}}} - 1}} = }\\ {{2^{ - \frac{1}{4}\left( {1 + 1.28\frac{{{\lambda_u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{W} - 1}}\sum\limits_{m = 0}^\infty {{2^{ - m}}{2^{ - m\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{{3l}}{{4W}}}}} } \end{array} $ | (19) |
其中(c)采用均值不等式,将式(19)代入式(9)中,业务覆盖率可以取得最大值:
| $ \begin{array}{*{20}{c}} {{{\bar {\mathscr{P}}}_l} \ge \int_{{l_{\min }}}^\infty {\sum\limits_{k = 1}^K {{\mathscr{S}_k}{2^{ - \frac{1}{4}\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{l}{W} - 1}}} } \times }\\ {\sum\limits_{m = 0}^\infty {{2^{ - m}}{2^{ - m\left( {1 + 1.28\frac{{{\lambda _u}{\mathscr{S}_k}}}{{{\lambda _k}}}} \right)\frac{{3l}}{{4W}}}}} \frac{{\theta l_{\min }^\theta }}{{{l^{\theta + 1}}}}{\rm{d}}l} \end{array} $ | (20) |
以下证明方法类似于定理2,不再详细说明.
| [1] | Coskun C C, Ayanoglu E. Energy-efficient base station deployment in heterogeneous networks[J]. IEEE Wireless Communications Letters, 2014, 3(6): 593–596. doi: 10.1109/LWC.2014.2356203 |
| [2] | Yunas S, Valkama M, Niemela J. Spectral and energy efficiency of ultra-dense networks under different deployment strategies[J]. IEEE Communications Magzine, 2015, 53(1): 90–100. doi: 10.1109/MCOM.2015.7010521 |
| [3] | Hu Liang, Kovacs I Z, Mogensen P, et al. Optimal new site deployment algorithm for heterogeneous cellular networks[C]//VTC 2011-Fall. San Francisco: IEEE Press, 2011: 1-5. |
| [4] | Peng Jinlin, Hong Peilin, Xue Kaiping. Energy aware cellular deployment strategy under coverage performance constraints[J]. IEEE Transactions on Wireless Communications, 2015, 14(1): 69–80. doi: 10.1109/TWC.2014.2329858 |
| [5] | Feng Jianyuan, Feng Zhiyong, Wei Zhiqing, et al. Optimal base station density in ultra densification heterogeneous network[C]//WCNC 2015. New Orleans: IEEE Press, 2015: 1452-1457. |
| [6] | Lee D, Zhou Sheng, Niu Zhisheng. Spatial modeling of scalable spatially-correlated log-normal distributed traffic inhomogeneity and energy efficient network planning[C]//WCNC 2013. Shang Hai: IEEE Press, 2013: 1285-1290. |
| [7] | Wang Shaowei, Zhao Wentao, Wang Chonggang. Budgeted cell planning for cellular networks with small cells[J]. IEEE Transcations on Vehicular Technology, 2015, 64(10): 4797–4806. doi: 10.1109/TVT.2014.2366783 |
| [8] | Xiang Lin, Ge Xiaohu, Wang Chengxiang. Energy efficiency evaluation of cell networks based on spatial distribution of traffic load and power consumption[J]. IEEE Transcations on Wireless Communications, 2013, 12(3): 961–973. doi: 10.1109/TWC.2013.011713.112157 |
| [9] | Stoyan D, Kendall W S, Mecke J. Stochastic geometry and its applications[M]. New York: Wiley, 1996: 223-227. |
| [10] | Singh S, Dhillon H S, Andrews J G. Offloading in heterogeneous networks:modeling, analysis and design insights[J]. IEEE Transcations Wireless Communications, 2013, 12(5): 2484–2497. doi: 10.1109/TWC.2013.040413.121174 |
| [11] | Cao Dongxu, Zhou Sheng, Niu Zhisheng. Optimal combination of base station densities for energy-efficient two-tier heterogeneous cellular networks[J]. IEEE Transcations Wireless Communications, 2013, 12(9): 4350–4362. doi: 10.1109/TWC.2013.080113.121280 |


