2. 西安中电科西电科大雷达技术协同创新研究院有限公司, 西安 710071;
3. 电子信息系统复杂电磁环境效应国家重点实验室, 河南 洛阳 471003
针对现有欠定盲分离混合矩阵估计方法中存在的估计精度低以及时间复杂度高等缺点,提出一种基于相似度检测的欠定混合矩阵估计方法.该方法能够在没有任何先验信息的条件下自适应地估计出源信号数目以及混合矩阵,而且不需要进行迭代,时间复杂度低.仿真结果表明,与现有的一些混合矩阵估计方法,如改进K-均值聚类法和拉普拉斯势函数法相比,所提出的方法在源信号数目估计准确率、混合矩阵估计精度以及时间复杂度等方面都具有明显优势.
2. Collaborative Innovation Center of Information Sensing and Understanding, Xi'an 710071, China;
3. State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, Henan Luoyang 471003, China
A new algorithm based on similarity measurement was proposed in order to address the issue of low estimation accuracy and high computational complexity in the existing algorithms for underdetermined mixing matrix blind estimation. The proposed algorithm can estimate the number of source signals and the mixing matrix automatically without any prior information or much iteration. Compared with the existing algorithms such as the K-means clustering and the Laplace's potential function method, the simulations turn out that the proposed has obvious advantages in the estimation accuracy of the number of source signals and the estimation precision of mixing matrix and the computational complexity.
盲源分离是指在不知道源信号任何先验信息以及信道混合矩阵的前提下,仅仅根据接收到的观测信号来估计各源信号的过程.关于盲源分离技术的研究已成为国际上信号处理领域的一个热点,并且已经广泛应用于数字通信、图像处理、生物医学、语音信号处理等领域.欠定盲分离是盲源分离中的一种病态混叠情况,由于欠定盲分离中系统是不可逆的,所以用于求解超定或正定盲分离的传统算法如联合对角化算法[1-2]、固定点算法[3]、等变自适应分解算法[4]等不再适用于欠定盲分离.
对于欠定盲分离问题的求解,“二步法”是一种最常用的分离方法,即首先根据观测信号估计出混合矩阵,然后再进行源信号恢复.对于欠定混合矩阵的估计,常用的方法有K-均值聚类法[5]、势函数法[6]、模糊聚类法[7]等. Li等[8]提出了利用K-均值算法来估计混合矩阵,但算法中存在初始聚类中心难以选取和普适性不强等缺点. Sun等[9]提出了一种基于密度的空间聚类与霍夫变换相结合的混合矩阵估计算法,算法运算复杂度较高,对于存在多路接收信号时的情况实时性不强.谭等[10]提出了一种基于模糊聚类的方法,但算法抗噪能力弱.
针对现有的欠定混合矩阵估计方法中存在的缺点,提出了一种基于相似度检测的欠定混合矩阵估计方法,不仅能够自适应地估计出源信号数目,而且能够以较高的精度计算出混合矩阵,运算复杂度低.
1 欠定盲分离数学模型欠定盲源分离就是当接收信号个数小于源信号个数时,在不知道源信号先验信息以及信道混合矩阵的条件下,仅仅根据观测到的混合信号估计出源信号的过程.对于线性瞬时混合情况下的欠定盲分离,可用数学模型表示为
| $ \mathit{\boldsymbol{x}}\left( t \right) = \mathit{\boldsymbol{As}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right) $ | (1) |
其中:s(t)=[s1(t), s2(t), …, sn(t)]T为n维源信号矢量;x(t)=[x1(t), x2(t), …, xm(t)]T为m维观测信号矢量,n>m;A为m×n混合矩阵,A=[a1, a2, …, an],ai(i=1, 2, …, n)为A中的列向量,每个源信号si对应一个ai;n(t)为高斯白噪声,t为观测时刻,t=1, 2, …, T.
目前针对欠定盲源分离问题的研究,要求源信号具有一定的稀疏性.只要源信号在某一个域如时域、频域、时频域等内是稀疏的,就能够实现各源信号的分离.以源信号在时域具有稀疏性为例,假设在时刻t,只有源信号si取值占优,其他源信号的幅度取值较小或为零,则可将式(1)写为
| $ \mathit{\boldsymbol{x}}\left( t \right) = {\mathit{\boldsymbol{a}}_i}{s_i}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right),t = {i_1},{i_2}, \cdots ,{i_p} $ | (2) |
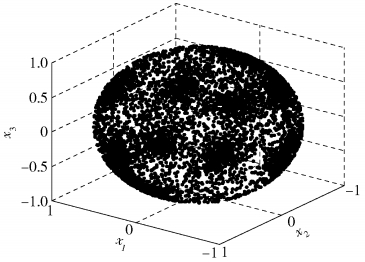
由式(2)可以看出,在t=i1, i2, …, ip时刻,由于源信号的稀疏性,观测信号采样点聚集在ai方向上,呈线聚特性.因此只要对所有时刻的观测信号采样点x(t)进行聚类分析,便可得到混合矩阵A的初步估计.若将观测信号的每一个采样数据点进行归一化处理,由于观测信号的线聚特性,同一个ai方向上的采样数据点则会聚集在以原点为圆心的单位球面上的某一个区域上. 图 1所示为观测通道数目m=3,源信号数目n=5时,对观测信号采样点进行归一化后的分布情况.其中,为保证一般性,源信号为Matlab随机生成的稀疏信号,混合矩阵A为3行5列的高斯随机矩阵.由图 1可知,采样数据点在以原点为圆心的单位超球面上具有相应的聚类特征.
|
图 1 m=3,n=5时的观测信号采样点分布 |
若源信号在时域上不具有稀疏性,则可以对观测信号进行适当的线性变换,如傅里叶变换、小波变换等,使之变换到相应的稀疏域再进行盲分离.在不考虑噪声的情况下,其变换原理为
| $ \mathit{\boldsymbol{X}}\psi = \mathit{\boldsymbol{AS}}\psi $ | (3) |
其中:X为观测信号采样点矩阵,矩阵中的每一列表示一个采样点;ψ为相应的线性变换;A为混合矩阵.根据线性变换原理,可进一步将式(3)表示为
| $ {\mathit{\boldsymbol{C}}_{\rm{x}}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{C}}_{\rm{s}}} $ | (4) |
其中:Cx为观测信号在变换域内的表达形式,Cs为源信号在变换域内的表达形式.由于线性变换ψ是可逆的,所以在相应的变换域内,只要源信号是稀疏的,依然满足式(2)所示的线性瞬时混合模型,并不影响混合矩阵A的估计和最后的源信号恢复.
2 基于相似度检测混合矩阵估计 2.1 观测信号预处理如图 1所示,对于时域稀疏的源信号或者经过相应的线性变换后,在相应的变换域内呈现稀疏性的源信号,经过信道后,在得到观测信号中,由于传输环境和噪声的影响,往往存在大量的异常值以及噪声点,以至于观测信号的聚类特征不够明显.因此需要对观测信号进行预处理,包括提取出观测信号采样点中的高能量采样点和高密度采样点.
首先为了更加精确地估计混合矩阵,利用式(5)除去观测信号采样点中的低能量采样点,保留下高能量采样点,组成一个高能量点矩阵.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_1} = \left\{ {\mathit{\boldsymbol{x}}\left( t \right)\left| {{{\left\| {\mathit{\boldsymbol{x}}\left( t \right)} \right\|}_2}} \right. \ge \alpha \max \left\{ {{{\left\| {\mathit{\boldsymbol{x}}\left( t \right)} \right\|}_2}} \right\}} \right\},}\\ {t = 1,2, \cdots ,T} \end{array} $ | (5) |
其中:‖x(t)‖2表示求取矢量x(t)的二范数,α∈[0.1, 0.5],X1中的每一列代表一个采样点.对X1中保留下来的采样点进行归一化:
| $ \mathit{\boldsymbol{x}}\left( t \right) = \frac{{\mathit{\boldsymbol{x}}\left( t \right)}}{{{{\left\| {\mathit{\boldsymbol{x}}\left( t \right)} \right\|}_2}}},t = 1,2, \cdots ,N $ | (6) |
其中N为X1中的总列数,即经过剔除低能量采样点后保留下来的样本点数目.
其次要搜索出高能量采样点矩阵X1中的高密度采样点.定义样本点之间的夹角为
| $ \begin{array}{*{20}{c}} {{\theta _{i,j}} = \arccos \left( {\frac{{\left| {\sum\limits_{k = 1}^m {{\mathit{\boldsymbol{x}}_i}\left( k \right){\mathit{\boldsymbol{x}}_j}\left( k \right)} } \right|}}{{{{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|}_2}{{\left\| {{\mathit{\boldsymbol{x}}_j}} \right\|}_2}}}} \right),}\\ {i = 1,2, \cdots ,N,j = = 1,2, \cdots ,N} \end{array} $ | (7) |
其中:θi, j为X1中第i个样本点和第j个样本点之间的角度,k为每个样本点矢量中的第k个元素,|·|表示取绝对值.样本点经过归一化,因此有‖xi‖2=1,‖xj‖2=1,故式(7)可变为
| $ {\theta _{i,j}} = \arccos \left( {\left| {\sum\limits_{k = 1}^m {{\mathit{\boldsymbol{x}}_i}\left( k \right){\mathit{\boldsymbol{x}}_j}\left( k \right)} } \right|} \right) $ | (8) |
在单位球面上,属于同一聚类的观测信号采样点分布相对紧密,各采样点之间的夹角较小,而不属于同一聚类的观测信号采样点之间的夹角较大,因此各观测信号采样点间的角度可作为各采样点之间相似关系的度量.
对于任意一个观测信号采样点p,将距离其最近的d个采样点组成一个样本集合,该集合称为p的邻域D,d为邻域D的邻域容量,其邻域半径rdp即为点p与这d个采样点之间距离的最大值,即
| $ r_d^p = \max \left\{ {{\rm{dist}}\left( {p,q} \right)\left| {q \in D} \right.} \right\} $ | (9) |
笔者利用对象p与q之间的角度大小来替代欧氏距离.如果采样点p为高密度采样点,则其样本邻域内的采样点分布较为密集,即在一定的邻域容量条件下,与低密度采样点相比,其邻域半径更小.根据此原理进行高密度采样点的提取.
在提取高密度采样点前,首先根据观测信号采样点数据集合本身的分布特性来设置一个邻域容量d,对于d的取值不宜太大,一般不超过所求聚类中最小聚类的采样点数,d的取值一般在βN左右,N为高能量采样点数目,β∈[0.01, 0.05].
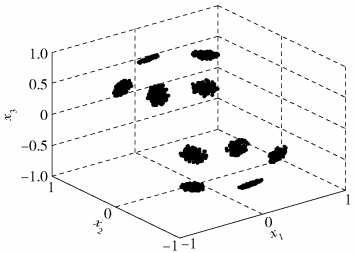
邻域容量d确定以后,进一步求出各个采样点的领域半径,并判断是否为高密度采样点.通过式(8)计算初始角度矩阵G,G={θi, j|1≤i≤N, 1≤j≤N},G是一个N×N的对称阵.对G的每一行分别进行升序排列,得到排序角度矩阵W,这样,W的第k(k=1, 2, …, T)列中的元素值即表示在邻域容量为k时各采样点所对应的邻域半径.对W中的第d列元素进行求均值,得到判别阈值rd.由于属于同一个聚类中的采样点集聚密度较大,所以当邻域容量为d时,聚类中各采样点的邻域半径较小,而对于噪声点和异常值不属于任何一个聚类,其集聚密度一般较小,其邻域半径的值一般较大.根据此特点,保留下邻域半径小于判别阈值rd的采样点,组成高密度采样点矩阵X2,其分布情况如图 2所示.
|
图 2 经过预处理得到的高密度采样点 |
由于源信号si的取值可正可负,由式(2)可知,采样点x(t)和-x(t)聚集在同一个ai方向上,经归一化后,同一个源信号所对应的采样点在单位超球面上关于原点对称,形成2个聚类,在进行混合矩阵估计时,这样的2个聚类会被合并为一个聚类,即这2个聚类对应的是同一个源信号si.因此,在图 2中采样数据点聚集的类数是源信号个数的2倍.
2.2 源信号数目估计和混合矩阵估计经过预处理后得到的高密度采样点,其聚类特性变得更加明显,而且在高密度采样点矩阵X2中,当邻域容量为d时, 每个高密度采样点的邻域半径rdk(k=1, 2, …, M)总是小于判别阈值rd,其中M为高密度矩阵X2中观测信号采样点的个数.而且,d的取值较小,因此,通常情况下各高密度采样点与其邻域范围内的其他采样点会存在于同一个聚类之中.利用式(8)重新构建一个用以衡量高密度矩阵X2中各采样点之间相似程度的角度矩阵:
| $ \mathit{\boldsymbol{\hat \theta }} = \left( {\begin{array}{*{20}{c}} {{{\hat \theta }_{11}}}&{{{\hat \theta }_{12}}}& \cdots &{{{\hat \theta }_{1M}}}\\ {{{\hat \theta }_{21}}}&{{{\hat \theta }_{22}}}& \cdots &{{{\hat \theta }_{2M}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{{\hat \theta }_{M1}}}&{{{\hat \theta }_{M2}}}& \cdots &{{{\hat \theta }_{MM}}} \end{array}} \right) $ | (10) |
其中
定义1 λ-截矩阵:对于一个给定的矩阵R,将矩阵中小于λ的元素置为0,大于λ的元素置为1,得到一个新的矩阵
根据角度矩阵
利用得到的λ-截矩阵,对高密度采样点矩阵X2中的采样点进行聚类,得到初步的分类Y={
考虑到实际传输环境中信道参数和噪声的影响,可能会存在混合矩阵中某2列相似度较高的情况,致使这2列对应的2个聚类比较接近,甚至存在交叠的部分,从而错误地形成一个大的聚类.因此在初步得到的聚类Y={
对于得到的分类Y={
|
|
表 1 δ的取值与源信号数目估计准确率的关系 |
经过校正后,得到一组更新后的分类
| $ {\mathit{\boldsymbol{a}}_j} = \frac{1}{{{B_j}}}\sum {{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over X} }}}_j}} ,j = 1,2, \cdots ,K' $ | (11) |
其中Bj为分类
综上所述,基于相似度检测的欠定混合矩阵估算法的主要实现流程如下.
步骤1 对接收到的观测信号利用式(5)提取出高能量采样点,并归一化,参数α=0.1.
步骤2 提取高密度采样点.
1) 计算初始角度矩阵G=arccos (|X1TX1|);
2) 计算排序角度矩阵W=sort(G),sort(·)表示对矩阵的每一行进行升序排序;
3) 设置邻域容量d=βN,参数β=0.03;
4) 计算判别阈值rd=E(W(:, d)),W(:, d)表示矩阵W的第d列元素,E(·)表示求均值;
5) 保留下邻域半径小于判别阈值rd的采样点,组成高密度采样点矩阵X2.
步骤3 进行初步的聚类划分.
1) 构建角度矩阵
2) 根据
3) 根据λ-截矩阵和高密度采样点矩阵X2,得到初步的聚类划分
步骤4 对各聚类进行评估和校正.
1) 根据角度矩阵,找到各分类
2) 若θmax≤rd+δ,聚类保持不变,否则利用FCM方法将
步骤5 根据校正后的聚类
在分析所提算法的时间复杂度时,以迭代次数和每次迭代中的乘法次数作为计算复杂度评价准则,并与改进K-均值聚类法[5]和拉普拉斯势函数法(LMMPF,Lapulace mixed model potential function)[6]进行了比较.
在文献[5]的改进K-均值方法中,需要事先进行采样点预处理,并给定一组聚类中心数目[εmin, εmax],在不同聚类数目的情况下,计算初始聚类中心,然后再根据初始聚类中心进行K-均值聚类,并计算出聚类结果的戴维森堡丁指数(DBI,Davies-Bouldin index),最后通过不同聚类数目下DBI指标值的大小来确定最优的聚类数目.其总的计算复杂度为
| $ {P_{{\rm{K - means}}}} = O\left( {\left( {{\varepsilon _{\max }} - {\varepsilon _{\min }} + 1} \right)\left( {\alpha {m^2}T + \left( {{\tau _0} + 1} \right)I{T_0}} \right)} \right) $ | (12) |
其中:α为常数,m为接收传感器个数,T为采样点总个数,I为设定的聚类数目,τ0为K-均值迭代次数,T0为预处理后的采样点个数.文献[6]中的LMMPF法需要预先估计2个参数,并将所有的观测数据作为初始聚类中心处理,其计算复杂度为
| $ {P_{{\rm{LMMPF}}}} = O\left( {T + \alpha {\tau _1}{T^2} + {\tau _2}r{T^2}} \right) $ | (13) |
其中:a为常数,τ1为参数估计时需要的迭代次数,τ2为计算聚类中心时需要的迭代次数,r为算法中计算出的参数值.
对于所提出的方法,其中观测信号预处理和提取高密度采样点的复杂度为
| $ {P_1} = O\left( {mT + {m^2}{T_2}} \right) $ | (14) |
其中:m为接收传感器个数,T2为高能量采点的总数目.而在源信号数目及混合矩阵估计步骤中,复杂度为
| $ {P_2} = O\left( {{m^2}M + bM + {\tau _3}L} \right) $ | (15) |
其中:M为高密度采样点的总数目,b为常数,L为需要校正的聚类中的采样点数目,τ3为FCM重新划分聚类时需要的迭代次数.若聚类无需进行校正时,则τ3L=0.由于L < M < T2 < T,因此所提方法的总计算复杂度为
| $ \begin{array}{*{20}{c}} {{P_3} = O\left( {mT + {m^2}{T_2} + {m^2}M + bM + {\tau _3}L} \right) < }\\ {O\left( {\left( {2{m^2} + m + \beta + {\tau _3}} \right)T} \right)} \end{array} $ | (16) |
由上述分析可知,LMMPF法的复杂度要远远高于其他2种方法,其复杂度的量级为O(T2),而改进K-均值方法与所提方法复杂度的量级均为O(T).
4 算法仿真和结果分析下面将通过仿真来测试所提出算法在不同实验条件下的混合矩阵估计精度和运行时间,并与现有的改进K-均值算法和LMMPF法进行比较,说明该算法的优势.采用估计误差衡量各个算法的混合矩阵估计精度,估计误差的定义为
| $ e = \frac{{{{\left\| {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{\hat A}}} \right\|}_{\rm{F}}}}}{{{{\left\| \mathit{\boldsymbol{A}} \right\|}_{\rm{F}}}}} $ | (17) |
其中:A为真实的混合矩阵,
在仿真实验中利用Matlab产生随机的5路时域稀疏信号作为源信号,接收传感器数目m=3,源信号数学模型为
| $ \mathit{\boldsymbol{S}} = {\rm{randn}}\left( {n,T} \right) \odot \max \left( {0,{\rm{sign}}\left( {{\rm{rand}}\left( {n,T} \right) - v} \right)} \right) $ | (18) |
其中:S为源信号矩阵,矩阵中的每一行对应一路源信号;randn(·)用以生成服从标准正态分布的随机数;“⊙”表示求点积;rand(·)用以生成服从均匀分布的随机数;sign(·)为符号函数;T为采样数据长度;参数v的取值在[0, 1]之间,v的取值越大,信号的稀疏度越高,反之越小,实验中取v=0.9.源数目n=5,信号采样点数T=5 000.信噪比在6~22 dB之间,每个信噪比下仿真400次.为验证各个算法的普适性,每次仿真中所使用的高斯混合矩阵都重新随机生成,对应于不同的信道状态.
图 3所示为不同SNR下对各算法的源信号数目估计准确率的比较,与改进K-均值算法和LMMPF相比,所提出的算法具有更高的源信号估计准确率.

|
图 3 各算法源信号数估计准确度比较 |
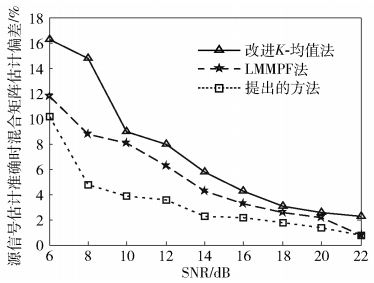
图 4所示为各算法的混合矩阵估计偏差比较,可见,在不同SNR下,使用所提出的方法得到的混合矩阵的估计误差最小.综合图 3和图 4的结果可知,所提出的欠定混合矩阵估计方法在源信号数目估计以及矩阵估计精度方面明显优于其他2种方法,在对应不同的信道状态时,能够保持较好的普适性.
|
图 4 各算法的混合矩阵估计偏差比较 |
图 5给出了在不同信噪比下各算法运行一次所需时间的比较结果,图中纵坐标采用以10为底的对数坐标来表示.由图 5可知,在不同信噪比下,LMMPF运行一次所需时间明显要长得多,时间复杂度最高,其次是改进K-均值聚类方法,所提出的方法的时间复杂度最低.

|
图 5 各算法运行一次所需要的时间比较 |
针对现有的欠定混合矩阵估计方法中存在的估计精度低以及时间复杂度高等缺点,提出了一种基于相似度检测的欠定混合矩阵估计方法.与现有的欠定混合矩阵估计算法相比,所提方法在矩阵估计精度和时间复杂度方面都具有明显的优势,实验仿真结果也进一步验证了所提算法具有较好的普适性,在非理想的通信环境中依然适用.
| [1] | Cardoso J F. Source separation using higher order moments[C]//1989 International Conference on Acoustics, Speech, and Signal Processing. [S. l. ]: IEEE, 1989: 2109-2112. |
| [2] |
冯大政, 保铮, 张贤达. 信号盲分离问题多阶段分解算法[J]. 自然科学进展, 2002, 12(5): 378–382.
Feng Dazheng, Bao Zheng, Zhang Xianda. Multistage decomposition algorithm for blind source separation[J]. Progress in Natural Science:Materials International, 2002, 12(5): 378–382. |
| [3] | Learned-Miller E G, Iii J W F. ICA using spacings estimates of entropy[J]. Journal of Machine Learning Research, 2003, 4(4): 1271–1295. |
| [4] | Cardoso J F, Laheld B H. Equivariant adaptive source separation[J]. IEEE Transactions on Signal Processing, 1996, 44(12): 3017–3030. doi: 10.1109/78.553476 |
| [5] | Fu Weihong, Ma Lifen, Li Aili. Blind estimation of underdetermined mixing matrix based on improved K-means clustering[J]. Journal of Systems Engineering and Electronics, 2014, 36(11): 2143–2148. |
| [6] | Zhang Ye, Fang Yong. A new method to estimate the number of the sources for underdetermined blind separation based on Lapulacial potential function[J]. Signal Processing, 2009, 25(11): 1719–1725. |
| [7] | Li Yibing, Nie Wei, Ye Fang, et al. A mixing matrix estimation algorithm for underdetermined blind source separation[J]. Circuits, Systems, and Signal Processing, 2016, 35(9): 3367–3379. doi: 10.1007/s00034-015-0198-y |
| [8] | Li Yuanqing, Cichocki A, Amari S. Analysis of sparse representation and blind source separation[J]. Neural Computation, 2004, 16(6): 1193–1234. doi: 10.1162/089976604773717586 |
| [9] | Sun Jiedi, Li Yuxia, Wen Jiangtao, et al. Novel mixing matrix estimation approach in underdetermined blind source separation[J]. Neurocomputing, 2015, 173(P3): 623–632. |
| [10] |
谭北海, 杨祖元, 周郭许, 等. 欠定盲分离中源的个数估计和分离算法[J]. 中国科学:信息科学, 2009, 39(3): 349–356.
Tan Beihai, Yang Zuyuan, Zhou Guoxu. Source number estimation and separation algorithms of underdetermined blind separation[J]. Scientia Sinica Informationis, 2009, 39(3): 349–356. |


