2. 广东德风科技有限公司 工程部, 广东 528437
针对大型风机叶片裂纹故障声学诊断问题,提出一种非接触式的叶片状态远程在线声学监测系统,给出了叶片裂纹故障的声学特征自适应提取方法.首先设计了面向复杂环境噪声的原始声信号预处理算法,然后采用1/6倍频程粗略刻画叶片声信号的频谱总体变化趋势,提取无量纲的倍频程能量比构造支持向量机分类器的输入特征向量,最后引入主成分分析法自适应的优化高维特征空间.风场实测数据验证了该算法的有效性.
2. Engineering Department, Guangdong Define Energy System Co. Ltd, Guangdong 528437, China
To solve the problem of crack detection of large turbine blades, the author proposed a non-contact online acoustic health monitoring system and studied in-depth on the adaptive crack feature extraction method. Firstly, a preprocessing algorithm is well designed to remove the complex background noise. Then 1/6 octave technique is used to reveal the spectrum change of acoustic signal roughly, and concluded that the octave energy ratios are extracted as input feature vector of the support vector machine classifier. Finally, the principal component analysis is introduced to optimize the high dimensional feature space adaptively. The measured data from wind field validates the effectiveness of proposed method.
叶片是风电机组的重要部件之一.由于长期运行在交变载荷和恶劣环境中,极易发生开裂等故障.随着风机服役时间的增加,叶片故障问题不断凸显.由于风机分布范围广、维护人员数量有限等原因,现有的人工定期巡检模式存在较大的安全隐患,亟需发展叶片健康自动监测和预警技术.
近年来,针对风机叶片故障诊断问题,发展了多种声学检测技术,如超声波、声发射、振动检测等.例如:Raišutis等[1]利用超声波检测技术识别风机叶片分层、缺胶等内部结构缺陷,该技术能够准确定位缺陷的位置;Joosse等[2]与Blanch等[3]引入声发射技术检测叶片的损伤区域,赵新光等[4]和杜文超等[5]研究了基于小波分析的叶片声发射信号的特征提取方法,能够识别出不同类型的损伤;Pratumnopharat等[6]给出了基于振动信号的风机叶片损伤识别方法,张保钦等[7]进一步研究了基于振动信号分析的叶片机械故障预测方法,等等.上述研究对于解决风机叶片故障诊断问题具有一定的理论意义和应用价值.需要说明的是,一方面,超声波检测主要适用于叶片出厂前的静态检测,声发射与振动等动态检测需要在叶片上安装传感器,可能破坏叶片的原有结构,且安装困难.另一方面,尽管动态检测方法在实验室环境下取得了良好的效果,但是,由于未充分考虑实际应用中传感器拾取的信号受机舱噪声与其他复杂环境背景噪声的耦合影响,可能导致虚警率过高,无法满足实际工程需求.
针对上述问题,本文首先设计一种非接触式的风机叶片远程在线声学监测系统,基于此,重点研究给出一种复杂背景噪声下叶片裂纹故障声学特征自适应提取方法,结合实测数据验证算法的有效性.
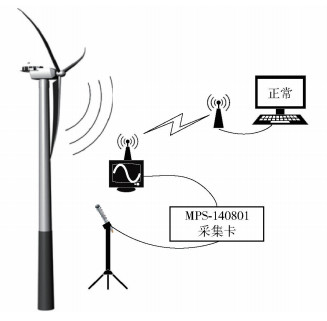
1 算法描述 1.1 远程在线监测系统结构叶片声学监测系统结构如图 1所示,由传感器采集模块、前端数据处理模块、通信模块和监控管理中心组成.
|
图 1 叶片远程在线声学监测系统结构 |
鉴于人耳能够直接分辨出故障与正常叶片,传感器选型时只要保证其频响范围涵盖20~20 kHz范围.前期实验结果表明,叶片旋转的下风侧的信噪比优于上风侧,因此,可依据风场常年的主导风向的先验知识确定传感器的安装角,以获取信噪比较高的声信号.此外,传感器可安装在塔门附近,避免塔筒顶部的机械噪声的影响,且便于安装维护.
前端数据处理系统直接安放在塔筒底部舱门内,减小对采集系统抗高低温的性能要求.通过对检测声信号的实时处理,诊断叶片健康是否存在安全隐患.如果叶片发生故障,通过现有的网络基础设施将诊断结果发送到远程监控管理中心,继而及时通知风场的维护人员前去检修.
1.2 检测声信号预处理叶片长期运行在野外,不但经受风沙、雨雪、极端温度、阵风等恶劣环境的影响,而且受风电机组输入力作用也异常复杂,导致实际采集的声信号包含了各种复杂、多变的强背景噪声,如风声、雷声、雨声、变桨噪声等.叶片早期故障时,能量较为微弱,极易掩盖在强背景噪声中.由于实验条件限制,现有采集的叶片声信号所包含的背景噪声主要为风噪.目前,风机的启动条件一般为平均风速不小于3.5 m/s,当风速达到12 m/s时,风噪声的声压级高达100 dB.相比于其他的背景噪声,风噪的影响严重且常态,因此,在提取叶片声学故障特征之前必须滤除风噪.
研究结果表明:风噪的频谱能量一般主要集中在200 Hz以下,而风机叶片开裂等故障产生的声信号的频率范围较宽(可达几十kHz).考虑到信号高频成分衰减较快,且检测传声器距离叶片较远,实际传感器采集的信号高频成分的能量极其微弱,不利于故障的判断.因此,采用带通滤波器对原始声信号进行预处理.
为使通带内频率响应曲线最大限度平坦,选用巴特沃斯带通滤波器,其平方幅频响应函数为
| $ {H^2}\left( p \right) = \frac{1}{{1 + {{\left( {p/j{\mathit{\Omega }_c}} \right)}^{2N}}}} $ | (1) |
其中
| $ p = \frac{{{s^2} + {\mathit{\Omega }_u}{\mathit{\Omega }_l}}}{{s\left( {{\mathit{\Omega }_u} - {\mathit{\Omega }_l}} \right)}} $ | (2) |
其中:N为滤波器的阶数,Ωc为3 dB截止频率,Ωu为上限截止频率,Ωl为下限截止频率. N越大,通带内特性越平坦,过渡带越窄,滤波效果越好,但也带来计算量的显著增加.
综合考虑数据处理的效果与算法实时性的要求,滤波器的阶数取30~50.为了避免因通带过宽导致滤波后信号中仍存在大量强噪声以及因通带过窄导致部分有用信号被当作噪声滤掉,下限截止频率可选择为50~200 Hz,上限截止频率可选择为10~15 kHz.
1.3 特征提取与优化在正常工作状态下,风机叶片产生的声音主要为叶轮扫风声.随着叶片服役时间的增加,可能出现一些异常的响声.例如,叶片脱胶在启动阶段会出现“唰、唰”的声音,稳定运行后声音消失,外表面不平整则发出哨鸣声,等等.风机维护人员通过耳听的方式能够准确判断叶片的健康状态.说明,在信号层面上,相比于正常工作状态,故障声信号的频谱发生了显著变化.
刻画声信号频谱变化的方式有多种.工程应用中常采用倍频程来描述信号的频谱变化趋势.常用的倍频程方法有:1/1倍频程、1/3倍频程、1/6倍频程与1/12倍频程等,它们刻画频谱变化的能力有所差异.例如,1/1倍频程在1 kHz以上倍频程带范围较宽,1/12倍频程在1 kHz以下倍频程带范围较窄.前期分析发现,相比于正常风机,故障风机的能量凸起随机分布在200 Hz~5 kHz的某些窄带内,如低频段几十Hz、中高频段几百Hz.综合考虑算法的鲁棒性以及倍频程的高低频表征能力,采用1/6倍频程刻画声信号的差异性.具体计算方法如下:
首先,将100 Hz~10 kHz的声频范围分成若干恒定带宽比的频带.假设fu为上限截止频率,fd为下限截止频率,中心频率为fc,则满足如下关系:
| $ \left. \begin{array}{l} {f_{\rm{u}}} = {2^{1/6}}{f_{\rm{d}}}\\ {f_{\rm{c}}} = \sqrt {{f_{\rm{u}}}{f_{\rm{d}}}} \end{array} \right\} $ | (3) |
然后,计算各频带内声压级S,可得声信号的1/6倍频程谱线,其中,声压级计算方法为
| $ {\mathit{\boldsymbol{S}}_j} = 20{\rm{lb}}\left( {\frac{{{\mathit{\boldsymbol{P}}_j}}}{{{P_{ref}}}}} \right),j = 1,2, \cdots ,n $ | (4) |
其中:
实际故障诊断应用中,传感器测量的绝对值受测量位置、灵敏度、噪声等因素影响较大.为此,提取无量纲的频带能量比作为故障模式分类的特征,描述故障与正常风机叶片的频谱趋势差异.通过分析前期的实测数据发现,故障风机叶片在某些频段上突然会有明显的能量增加,反映在1/6倍频程谱上通常为2~3个频段有异常凸起.为了准确地刻画这种突变,将4个相邻的频带分为一组,以每组中前2个频段的声压级之和除以后2个频段的声压级之和作为倍频程能量比特征,具体的计算公式为
| $ {\mathit{\boldsymbol{R}}_{{\rm{SP}}{{\rm{L}}_i}}} = \frac{{{\mathit{\boldsymbol{S}}_i} + {\mathit{\boldsymbol{S}}_{i + 1}}}}{{{\mathit{\boldsymbol{S}}_{i + 2}} + {\mathit{\boldsymbol{S}}_{i + 3}}}},\;\;\;i = 1, \cdots ,m $ | (5) |
同时发现,上述凸起随着叶片故障位置、尺寸等不同而随机变化,为了自适应提取主要的特征分量和提高分类的精度,采用主成分分析法对所有能量比特征进行降维.主成分分析能将高维的数据通过线性变换投影到低维空间,且保留原有的绝大部分有用信息,降维过程中需要满足最小化维度间相关性和最大化各维度的方差.具体的声学特征优化步骤如下:
1) 构造输入样本矩阵.假设原始数据包含n个样本,每个样本有m个能量比特征,构造n行m列的原始特征矩阵Xn×m.
2) 零均值化特征矩阵的每一列,得到矩阵X′n×m:
| $ {{\mathit{\boldsymbol{X'}}}_{ij}} = {\mathit{\boldsymbol{X}}_{ij}} - \frac{{\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{X}}_{ij}}} }}{n},\;\;j = 1, \cdots ,m $ | (6) |
3) 计算协方差矩阵,获得各维度的方差(主对角线上元素)与不同维度间的相关系数(非对角线上元素),协方差矩阵的具体计算方法为
| $ \mathit{\boldsymbol{C}} = \frac{1}{{n - 1}}{{\mathit{\boldsymbol{X'}}}^{\rm{T}}}\mathit{\boldsymbol{X'}} $ | (7) |
4) 矩阵对角化.为了尽可能减小不同维度间的相关性,即让协方差矩阵中非对角线元素接近0,对协方差矩阵进行对角化处理,得到特征值矩阵Λ与特征向量矩阵Pm×m,对角化公式为
| $ {\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{CP}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} $ | (8) |
5) 自适应提取主成分.特征值矩阵的主对角线元素即为各维度的新方差,并按从大到小排序,筛选累计贡献率大于阈值的前k(k<m)个主成分,排列组成投影矩阵P′,对输入样本矩阵进行投影得到新的样本矩阵Y:
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{XP'}} $ | (9) |
假设正常与故障风机叶片的样本集表示为Y ={(xi, yi)|i=1, 2, …, n},xi∈ Rm,yi∈{-1, +1}.其中,n为样本总数,m为样本特征向量的维数,xi表示第i个样本,yi为第i个样本的类别标签,若xi为正常风机叶片,则yi=+1,反之,yi=-1.
以提取的无量纲1/6倍频程能量比特征作为输入向量,采用支持向量机(SVM,support vector machine)[8]训练建立风机叶片的故障分类器模型:
| $ \left. \begin{array}{l} \min \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{b}}} \right) = \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + C\sum\limits_{i = 1}^n {{\xi _i}} \\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;{\mathit{\boldsymbol{y}}_i}\left( {{\mathit{\boldsymbol{x}}_i}\mathit{\boldsymbol{w}} + \mathit{\boldsymbol{b}}} \right) - 1 + {\xi _i} \ge 0,{\xi _i} \ge 0 \end{array} \right\} $ | (10) |
其中,ξi为松弛变量,C为惩罚因子.通过拉格朗日函数构造及求解,可以确定最优的故障分类模型.其中,惩罚因子选取较为关键,取值范围为
| $ \frac{1}{N} < C < \frac{1}{{N\sigma }} $ | (11) |
其中:N表示样本数,σ表示控制的误差容忍率.
2 实验分析为了验证算法的有效性,现场采集了张家口尚义县麒麟山风场与承德围场县赛罕坝风场的故障与正常风机.其中,麒麟山风场的风机型号均为UP1500-82,机组容量1.5 MW,叶片故障的类型为前缘开裂;赛罕坝风场的风机型号均为UP2000-96S,机组容量2 MW,叶片故障的类型为后沿开裂,如图 2所示.测试系统由YG-201型传声器、MPS-140801采集卡以及集成LabVIEW采集软件的笔记本电脑构成,测试的叶片类型、位置及时长如表 1所示.

|
图 2 故障叶片(左麒麟山,右塞罕坝) |
|
|
表 1 数据集信息 |
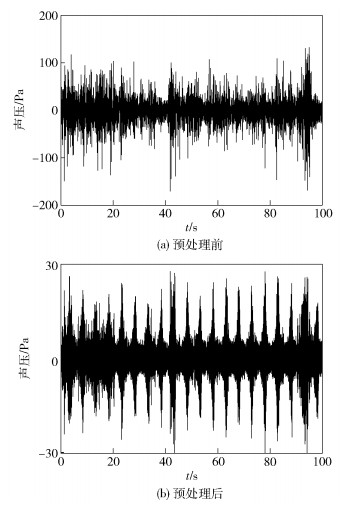
首先,对原始声信号进行预处理.设置带通滤波器的下限截止频率为100 Hz、上限截止频率10 kHz,滤波器阶数50.以麒麟山风场的Data 2为例,预处理前后时域波形如图 3所示.
|
图 3 预处理前后时域波形(Data2) |
可以看出,经过预处理以后叶片旋转的周期特性更加明显,且通过耳听可以分辨出原始信号中风噪基本得以滤除.
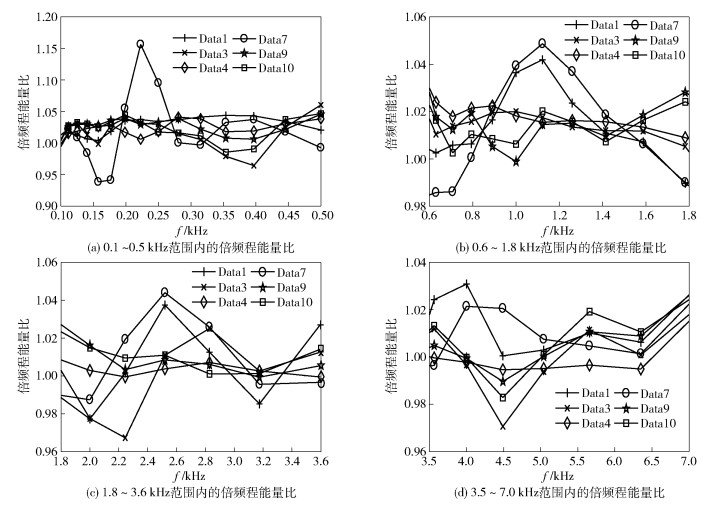
正常情况下,风机叶片的转速约为12~13 rpm,因此,叶片旋转一周的时间接近5 s.为保证每个样本均包含有效的故障特征,选择样本的长度为5 s,风机叶片数据共得到240个样本,其中,故障叶片样本96个,正常叶片样本384个.对样本集进行1/6倍频程分析,并提取无量纲的倍频程能量比特征(共39个),结果如图 4所示.可以看出,故障叶片大约在[200 Hz,260 Hz]、[1 000 Hz,1 300 Hz]、[2 300 Hz,2 800 Hz]和[3 500 Hz,4 500 Hz]范围内有明显凸起,且特征空间中包含一些无用特征.需要说明的是,同一类数据不同样本的能量比曲线可能有细微差异.
|
图 4 倍频程能量比特征提取 |
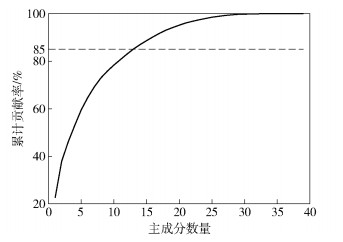
利用主成分分析法对原始特征空间进行降维优化,累计贡献率随主成分数量的变化关系如图 5所示.可以看出:保留信息量随着主成分数量的增加而增长,但当主成分数量达到35时,累积贡献率达到100,随后保持不变.本文综合考虑保留信息量最大化与计算量最小化两方面因素,设置累计贡献率的阈值为85%,最终得到的主成分数量为13.
|
图 5 主成分累计贡献率的变化曲线 |
为进一步验证所提出的叶片声学特征自适应提取方法的有效性,采用SVM对数据集进行分类实验.设置径向基函数作为核函数,误差容忍率σ为0.01,在(0.1,10)范围内对惩罚系数C进行寻优,同时对参数g进行寻优,结果如图 6所示,最优的惩罚系数为1.5,核宽度参数g为0.4.
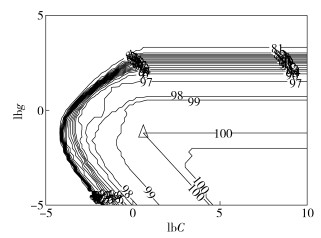
|
图 6 参数C、g的寻优结果 |
采用10折交叉验证法进行实验验证,具体做法为:将样本集随机平均分成10个子集,每一个子集都轮流作为测试集,其余9个子集作为训练集,结果取平均值.共进行10次交叉实验,结果如表 2所示.
|
|
表 2 实验结果 |
由于噪声等因素影响,同一类数据不同样本特征间存在一定的离散度,从而导致个别样本分类错误.由上述实验结果可以看出,10次十折交叉验证的结果均高于98%.为了进一步提高识别准确率和满足工程应用需求,可以连续判断两个周期,若诊断结果相同,则输出报警.因此,笔者提出的算法能够正确区分叶片的故障与正常状态,且具有较好的稳定性与泛化能力.
3 结束语针对大型风机叶片状态监测问题,提出一种非接触式叶片裂纹故障声学诊断方法.所提出的预处理算法能够有效去除风噪影响和分离出感兴趣的叶片声学信号,基于1/6倍频程和主成分分析法的故障特征自适应提取方法能够准确地刻画叶片裂纹故障与正常状态间频谱差异.最后,实验验证了方法的有效性.该方法可应用于大型风机叶片状态的现场实时监测,具有潜在的工程应用价值.
| [1] | Raišutis R, Jasiūnienė E, Žukauskas E. Ultrasonic NDT of wind turbine blades using guided waves[J]. Ultrasound, 2008, 63(1): 7–11. |
| [2] | Joosse P A, Blanch M J, Dutton A G. Acoustic emission monitoring of small wind turbine blades[J]. Journal of Solar Energy, 2002, 124(4): 1–11. |
| [3] | Blanch M J, Dutton A G. Acoustic emission monitoring of field tests of an operating wind turbine[J]. Key Engineering Materials, 2003, 245. |
| [4] | 赵新光. 基于声发射和小波分析的大型风力机叶片材料损伤识别研究[D]. 沈阳: 沈阳工业大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10142-2010063451.htm |
| [5] | 杜文超. 基于声发射技术的大型风力机叶片材料的损伤研究[D]. 南京: 南京航空航天大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041037.htm |
| [6] | Pratumnopharat P, Leung P S, Court R S. Application of Morlet wavelet in the stress-time history editing of horizontal axis wind turbine blades[C]//20122nd International Symposium on Environment Friendly Energies and Applications. Newcastle upon Tyne:IEEE press, 2012:396-401. |
| [7] |
张保钦, 雷保珍, 赵林惠, 等. 风机叶片故障预测的振动方法研究[J]. 电子测量与仪器学报, 2014, 28(3): 285–291.
Zhang Baoqin, Lei Baozhen, Zhao Linhui, et al. Research on vibration method of fan blade fault forcasting[J]. Journal of Electronic Measurement and Instrumentation, 2014, 28(3): 285–291. |
| [8] | Cortes C, Vapnik V. Support vector networks[J]. Machine Learning, 1995, 20(3): 273–297. |


