2. 河南机电职业学院, 郑州 451191
为了进一步研究Han-Kobayashi(HK)传输策略在多用户Z高斯干扰信道上的性能,在中等弱干扰条件下构造了多用户Z高斯干扰信道可达速率内、外界.通过将信息分割为公有信息和私有信息,优化每个用户的公有信息和私有信息之间的比例,得出一条多用户Z高斯干扰信道速率RHK;通过增加级联Z高斯干扰信道的约束条件得出了一条小于RHK的速率內界;利用精灵辅助方案,得出了大于RHK的两条速率外界.通过计算速率内、外界之差得出:在中等干扰下,利用HK策略所得到的速率距离信道容量小于1 bit·s-1·Hz-1;在弱干扰下,随着总用户数量的增加,利用HK策略所得到的速率RHK与信道容量之间距离逐渐逼近1 bit·s-1·Hz-1.
2. Henan Mechanical and Electrical Vocational College, Zhengzhou 451191, China
In order to further study the communication scheme of Han-Kobayashi (HK) on cascade Gaussian Z interference channel, a method of one inner bound and two outer bounds was proposed under weak and medium interference. In the scheme, as the transmitted information of both users split into common information and private information, a achieve rate RHK is obtained by optimizing the ratio between common and private information. An inner bound is proposed by adding a constraint on this channel which is less than RHK. Based on two genie-aided programs of two-user interference channel, two outer bounds were proposed by genie-aided which great than RHK. By analyzing the distance between the inner bound and outer bounds, HK type scheme can be achieved within a single bit per second per hertz (bit·s-1·Hz-1) of the capacity under medium interference and approach to a single bit per second per hertz (bit·s-1·Hz-1) of the capacity under weak interference as total number increasing.
追求更高传输速率和更高频谱效率是无线通信领域一个永恒的话题,其根本问题是如何提高网络信息容量.从原理上来说,提高网络信息容量,一方面需要增加网络的覆盖、提高信息的传输速率,另一方面用户密度的增加要求能有效解决小区间的干扰问题.近年来,多输入多输出(MIMO, multiple-input multiple-output)技术、空时编码技术、机会调度、现代信道编码(Turbo码、低密度奇偶校验码和Rateless码)等技术的出现,使得信道衰落和信道加性噪声对通信系统造成的影响越来越小.同时,中继协作技术的出现解决了信号的传播距离问题,在提高了网络覆盖性能的同时加剧了小区内、小区间和网络间的干扰.因此,干扰日益成为制约提升通信系统性能的瓶颈,如何消除干扰带来的影响成为无线通信网络的研究重点,同时用来描述用户之间干扰的干扰信道模型也成为了一类研究的热点模型[1].
然而,从干扰信道模型的提出[2]以来,中等弱干扰条件下的干扰信道容量限至今仍未确定.目前,该条件下的最佳速率区域是1981年由Han和Kobayashi提出的,其传输方案称为Han-Kobayashi(HK)传输策略[3].其思想是利用速率分裂技术将每个发射端的发送信息分成2部分:能够被每个接收端译出的公有信息和只能被相应接收端译出的私有信息.通过计算最优公有信息与私有信息比例获取最大可达速率. 2004年,Sanson[4]提出了一种退化的2用户干扰信道——2用户Z干扰信道,经过几年的研究,该信道的容量研究成果较为丰富,在所有干扰条件下其和速率容量限已确定.假定接收端已知延迟信道状态信息,Mohanty等[5]给出了该信道的自由度区域;Patel等[6]给出了多址认知Z干扰信道的可达速率区域;假定接收端已知混合状态信道信息,Mohanty等[7]给出了该条件下的Z干扰信道自由度区域;Shang[8]给出了MIMO Z干扰信道的部分容量界和和速率容量限;Costa[9]利用功率注水法在中等干扰强度下给出了2用户Z干扰信道速率可达区域;利用HK传输策略可得到2用户Z高斯干扰信道可达速率区域,Costa等[10]确定了该可达速率区域拐点处的斜率.然而,以上2用户Z干扰信道成果在3用户以上信道应用具有很大局限性.
近年来,由于多用户级联Z高斯干扰信道(CGZIC, cascade Gaussian Z interference channel)能够模拟高速路通信环境,开始引起了许多学者的关注,但至今为止该信道的容量研究成果仅限于3用户或特殊条件下的多用户CGZIC. Liu等[11]仅证明了3用户CGZIC下,利用HK传输策略得到的可达和速率距离和速率容量限最多0.5 bit·s-1·Hz-1. Mohanty等[12]基于干扰对齐方法,得出了3用户MIMO循环CGZIC的自由度区域.
笔者针对多用户CGZIC信道容量问题进行研究,主要利用Etkin,Tse和Wang[13]提出的内外界构建方法, 简称ETW方法,通过增加约束条件和引入精灵辅助技术,构造出N(N>2)用户CGZIC的传输速率內界和外界.同时,将2用户干扰信道最佳传输方案的HK传输方案推广至N(N>2)用户CGZIC.通过计算内外界之差,分析其可达速率与该信道容量限之间的距离.
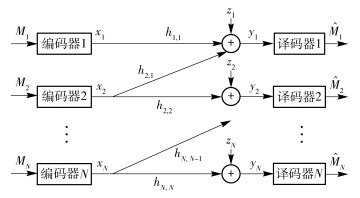
1 信道模型Wyner小区通信网络呈线性排列分布,每个基站只服务一个用户,除了最后一个用户,其余用户只受相邻一个小区的干扰.因此,CGZIC模型可用于描述该通信网络的下行信道,其信道模型如图 1所示.现实环境中,CGZIC模型可用来模拟高速公路、铁路、坑道及涵洞内部等通信环境,信道模型的表达式为
| $ \left. {\begin{array}{*{20}{c}} {{y_1} = {x_1} + {h_{2,1}}{x_2} + {z_1}}\\ {{y_2} = {x_2} + {h_{3,2}}{x_3} + {z_2}}\\ \vdots \\ {{y_N} = {x_N} + {z_N}} \end{array}} \right\} $ | (1) |
|
图 1 改进型Wyner信道模型 |
其中:xn为用户n的发送信息;yn为用户n的接收信息,且发射功率满足E[|xn|2]≤Pn;hn, i为用户n的发射端到用户i的接收端的信道系数;zn为高斯白噪声,zn~
根据HK方法,在发射端将每个用户发送的信息分为私有信息Wn和公有信息Un(n∈{1, 2, …, N})2部分.在接收端采用同时译码方法,通过调节每个用户私有信息与公有信息之间的比例,得到可达速率RHK.为了分析RHK与N用户CGZIC的信道容量限之间的距离,构造N用户CGZIC的速率内、外界,通过分析内、外界之差,判断出RHK与容量限之间的距离.
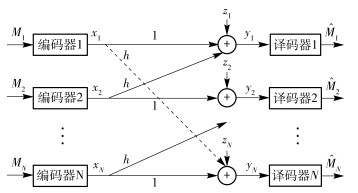
2 N用户CGZIC可达速率内界通过增加信道的约束条件,利用简化HK方法构造N用户CGZIC的可达速率.由于信道增加了约束条件,利用简化HK方法构造的可达速率,必定是N用户CGZIC的速率内界RIB,且满足RIB≤RHK.如图 2所示,假定第1个用户与第N个用户之间产生约束,即第N个用户的接收端受到来自第1个用户发射端的干扰,从而N用户CGZIC模型衍变成循环高斯干扰信道模型.同样考虑对称信道,根据文献[15]引理1和文献[16],定义γ(x)=lb(1+x),可得到循环高斯干扰信道的可达和速率为
| $ \begin{array}{*{20}{c}} {R\left( {{\lambda _1},{\lambda _2} \cdots ,{\lambda _N}} \right) = \sum\limits_{m = 1}^N {\gamma \left( {\frac{{{\lambda _n}P}}{{1 + {h^2}{\lambda _{n + 1}}P}}} \right)} + }\\ {\min \left\{ {\sum\limits_{n = 1}^N {\gamma \left( {\frac{{{{\bar \lambda }_n}P}}{{1 + {\lambda _n}P + {h^2}{\lambda _{n + 1}}P}}} \right)} ,} \right.}\\ {\sum\limits_{n = 1}^N {\gamma \left( {\frac{{{h^2}{{\bar \lambda }_n}P}}{{1 + {\lambda _{n - 1}}P + {h^2}{\lambda _n}P}}} \right)} ,}\\ {\left. {\frac{1}{2}\sum\limits_{n = 1}^N {\gamma \left( {\frac{{{h^2}{{\bar \lambda }_n}P + {{\bar \lambda }_{n - 1}}P}}{{1 + {\lambda _{n - 1}}P + {h^2}{\lambda _n}P}}} \right)} } \right\}} \end{array} $ | (2) |
|
图 2 增加约束条件的N用户CGZIC |
其中:λn为用户的分裂系数,λn=1-λn.
采用ETW方法,增加一些特殊约束,通过简单HK方案得出N用户CGZIC的速率内界.假定每个用户私有与公有信息的分配比例相同且为λ,并满足hP≥1.可达和速率[13]为
| $ \begin{array}{*{20}{c}} {{R_{{\rm{sum}} - {\rm{IB}}}} = N\min \left\{ {\underbrace {\frac{1}{2}\gamma \left( {{h^2}P + P} \right) + \frac{1}{2}\gamma \left( {1 + \frac{1}{{{h^2}}}} \right) - 1}_{{\beta _1}},} \right.}\\ {\left. {\underbrace {\gamma \left( {{h^2}P + \frac{1}{{{h^2}}}} \right) - 1}_{{\beta _2}}} \right\}} \end{array} $ | (3) |
则对称速率内界为
| $ \begin{array}{*{20}{c}} {{R_{{\rm{sum}} - {\rm{IB}}}} = \min \left\{ {\underbrace {\frac{1}{2}\gamma \left( {{h^2}P + P} \right) + \frac{1}{2}\gamma \left( {1 + \frac{1}{{{h^2}}}} \right) - 1}_{{\beta _1}},} \right.}\\ {\left. {\underbrace {\gamma \left( {{h^2}P + \frac{1}{{{h^2}}}} \right) - 1}_{{\beta _2}}} \right\}} \end{array} $ | (4) |
定义
| $ \begin{array}{*{20}{c}} {{\beta _1} = \left\{ {\left( {P,{h^2}P} \right):{h^2}P \ge 1 \cup P\left( {P + {h^2}P} \right) < } \right.}\\ {\left. {{h^4}{P^2}\left( {{h^2}P + 1} \right)} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\beta _2} = \left\{ {\left( {P,{h^2}P} \right):{h^2}P \ge 1 \cup P\left( {P + {h^2}P} \right) \ge } \right.}\\ {\left. {{h^4}{P^2}\left( {{h^2}P + 1} \right)} \right\}} \end{array} $ |
其中:β1为中等干扰区域,β2为弱干扰区域.为了能够随着干扰强度变化,形象地描述速率内界与点对点加性高斯白噪声(AWGN,additive white Gaussian noise)信道容量之间的关系,将式(4)除以点对点AWGN信道容量CAWGN,即
| $ \begin{array}{*{20}{c}} {\frac{{{R_{{\rm{IB}}}}}}{{{C_{{\rm{AWGN}}}}}} = }\\ {\frac{{\min \left\{ {\frac{1}{2}\gamma \left( {{h^2}P + P} \right) + \frac{1}{2}\gamma \left( {1 + \frac{1}{{{h^2}}}} \right) - 1,\gamma \left( {{h^2}P + \frac{1}{{{h^2}}}} \right) - 1} \right\}}}{{\gamma \left( P \right)}} \approx }\\ {\min \left\{ {1 - \frac{1}{2}\frac{{\gamma \left( {{h^2}P - 1} \right)}}{{\gamma \left( {P - 1} \right)}},\max \left\{ {\frac{{\gamma \left( {{h^2}P - 1} \right)}}{{\gamma \left( {P - 1} \right)}},1 - \frac{{\gamma \left( {{h^2}P - 1} \right)}}{{\gamma \left( {P - 1} \right)}}} \right\}} \right\}} \end{array} $ | (5) |
考虑在高信噪比条件下(h2P≫1, P≫1),且满足1≫h2,定义
| $ \frac{{{R_{{\rm{IB}}}}}}{{{C_{{\rm{AWGN}}}}}} \approx \min \left\{ {1 - \frac{\alpha }{2},\max \left\{ {\alpha ,1 - \alpha } \right\}} \right\} $ |
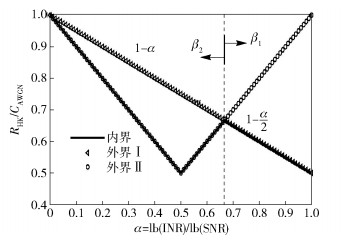
图 3所示为在β1和β2范围内,函数α根据不同干扰强度的取值.
|
图 3 N用户CGZIC速率内界、外界Ⅰ、Ⅱ与CAWGN的比值 |
根据总用户数量的奇偶性,在β1和β2范围内,采用2种精灵辅助模式,相应地提出N用户CGZIC的2条速率外界.
3.1 外界Ⅰ在β1范围内,提出一种较为紧致的速率外界.
3.1.1 N(奇数)用户CGZIC的速率外界定理1 总用户量为N(N为奇数变量,N>1)的CGZIC如图 4所示,该信道的对称速率外界为
| $ R_{{\rm{UB1}}}^{\rm{o}} = \frac{1}{N}\gamma \left( {\sqrt P } \right) + \frac{{N - 1}}{{2N}}\left( {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right) $ | (6) |

|
图 4 具有精灵辅助的N用户CGZIC |
证明 在发射端中,将第2个用户的信息x2分割为x21和x22相互独立的2部分;在接收端中,(N-1)/2个用户得到精灵给予的边信息.精灵辅助的具体方法如下:
1) 精灵部分辅助策略
第1个用户得到的边信息为s1,s1=x21.设xnm为用户n发送的码长为m的信息序列,ynm为用户n接收的码长为m的信息序列,snm为用户n码长为m的边信息序列,znm为用户n在接收码长为m序列时的噪声. x1和s1相互独立,有
| $ \begin{array}{*{20}{c}} {I\left( {\mathit{\boldsymbol{x}}_1^m;\mathit{\boldsymbol{y}}_1^m,\mathit{\boldsymbol{s}}_1^m} \right) = I\left( {\mathit{\boldsymbol{x}}_1^m;\mathit{\boldsymbol{s}}_1^m} \right) + I\left( {\mathit{\boldsymbol{x}}_1^m;\mathit{\boldsymbol{y}}_1^m\left| {\mathit{\boldsymbol{s}}_1^m} \right.} \right) = }\\ {I\left( {\mathit{\boldsymbol{x}}_1^m;\mathit{\boldsymbol{x}}_1^m + h\mathit{\boldsymbol{x}}_{22}^m + \mathit{\boldsymbol{z}}_1^m} \right)} \end{array} $ | (7) |
由此可见,得到精灵辅助的用户1只受到用户2私有信息的干扰.
如果x21的功率满足E[|x21|2]≥
| $ {R_1} = \gamma \left( {\frac{P}{{1 + \sqrt P - 1}}} \right) = \gamma \left( {\sqrt P } \right) $ | (8) |
因此,用户1的链路可看作是噪声服从Z1~
2) 精灵完全辅助策略
奇数用户Un得到的边信息为xn+1, n=1+2i,
利用边信息消除其他用户带来的干扰,使得用户{Un, n=1+2i,
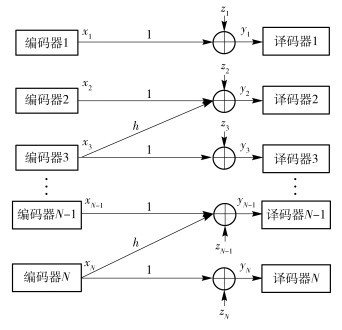
从而,当总用户数量为奇数时,利用该精灵辅助方案,CGZIC可看作是由一个点对点信道和(N-1)/2个2用户Z干扰信道构成的,如图 5所示.根据文献[4],当h<1时,这个信道的和速率容量为
| $ R_{{\rm{sum - capacity}}}^{\rm{o}} = \gamma \left( {\sqrt P } \right) + \frac{{N - 1}}{2}\left( {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right) $ | (9) |
|
图 5 复合信道模型 |
则得到一个N用户CGZIC速率外界为
| $ R_{{\rm{UB1}}}^{\rm{o}} = \frac{1}{N}\gamma \left( {\sqrt P } \right) + \frac{{N - 1}}{{2N}}\left( {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right) $ | (10) |
在高信噪比下,即P≫1, h2P≫1,且满足1≫h2,当总用户数量趋于无穷时,得出
| $ \frac{{R_{{\rm{UB1}}}^{\rm{o}}}}{{{C_{{\rm{AWGN}}}}}} \approx 1 - \frac{1}{a} $ | (11) |
证毕.
3.1.2 N(偶数)用户CGZIC的速率外界定理2 总用户量为N(N>2)的CGZIC如图 5所示,当N为偶数时,该信道的对称速率外界为
| $ R_{{\rm{UB1}}}^{\rm{e}} = \frac{1}{2}\left( {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right) $ | (12) |
证明 与总用户数量为奇数的信道相类似,总用户数量N为偶数的CGZIC中,用户{Un, n=2i,
| $ R_{{\rm{sum - capacity}}}^{\rm{e}} = \frac{N}{2}\left( {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right) $ | (13) |
| $ R_{{\rm{UB1}}}^{\rm{e}} = \frac{1}{2}\left( {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right) $ | (14) |
证毕.
高信噪比条件下,即P≫1, h2P≫1,且满足1≫h2,有
| $ \frac{{R_{{\rm{UB1}}}^{\rm{o}}}}{{{C_{{\rm{AWGN}}}}}} \approx 1 - \frac{1}{\alpha } $ | (15) |
针对总用户数量的奇偶性,在β1范围内得到了相应的速率内外界.通过计算速率内外界之差,从而判断利用HK方案得到的N用户CGZIC的速率内界与容量限之间的距离.
用户总数为奇数的用户速率内外界比较如下:
| $ \begin{array}{*{20}{c}} {R_{UB1}^{\rm{o}} - {R_{IB}} = }\\ {\frac{1}{N}\gamma \left( {\sqrt P } \right) + \frac{{N - 1}}{{2N}}\left[ {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right] - }\\ {\frac{1}{2}\gamma \left( {P + {h^2}P} \right) - \frac{1}{2}\gamma \left( {1 + \frac{1}{{{h^2}}}} \right) + 1 < }\\ {\frac{1}{N}\gamma \left( {\sqrt P } \right) - \frac{1}{{2N}}\gamma \left( {P + {h^2}P} \right) - \frac{1}{{2N}}\gamma \left( {1 + \frac{1}{{{h^2}}}} \right) + 1 < 1} \end{array} $ | (16) |
其中第1个不等式是根据文献[3]得出的.
用户总数为偶数的用户速率内外界比较如下:
| $ \begin{array}{*{20}{c}} {R_{{\rm{UB1}}}^{\rm{o}} - {R_{{\rm{IB}}}} = \frac{1}{2}\left[ {\gamma \left( {\frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( P \right)} \right] - }\\ {\frac{1}{2}\gamma \left( {P + {h^2}P} \right) - \frac{1}{2}\gamma \left( {1 + \frac{1}{{{h^2}}}} \right) + 1 < 1} \end{array} $ | (17) |
根据文献[13],式(17)中的不等式成立.因为RIB<RHK,且RHK<RUB1,所以利用HK方案得到的N用户CGZIC的速率区域RHK距离容量限在β1范围内小于1 bit·s-1·Hz-1bit.
如图 3所示,内界Ⅰ在β1范围内较为紧致,但在β2范围内很松弛.下面将构造在β2范围内较紧致的速率外界.
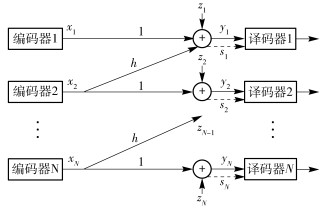
3.2 外界Ⅱ采用另一种精灵辅助方案,在β2范围内,提出一种较为紧致的速率外界.为避免给予用户过多的边信息,给各个接收端提供的信息不足以让它们完全消除受到的干扰,如图 6所示,辅助信息分别为
| $ \left. {\begin{array}{*{20}{c}} {{s_1} = h{x_1} + {z_N}}\\ {{s_2} = h{x_2} + {z_1}}\\ \vdots \\ {{s_N} = h{x_N} + {z_{N - 1}}} \end{array}} \right\} $ | (18) |
|
图 6 具有精灵辅助的N用户CGZIC模型 |
参考ETW方案,给出N用户CGZIC的另一条速率外界RUB2.
定理3 利用以上提出的精灵辅助方案,N用户CGZIC的和速率外界为
| $ {R_{{\rm{sum - UB2}}}} = \left( {N - 1} \right)\gamma \left( {{h^2}P + \frac{P}{{1 + {h^2}P}}} \right) + \gamma \left( {P + {h^2}P} \right) $ | (19) |
证明
| $ \begin{array}{*{20}{c}} {m\sum\limits_{n = 1}^N {{R_n}} \le \sum\limits_{n = 1}^N {I\left( {\mathit{\boldsymbol{x}}_n^m;\mathit{\boldsymbol{y}}_n^m,\mathit{\boldsymbol{s}}_n^m} \right) + m{\varepsilon _m}} \le }\\ {\sum\limits_{i = 1}^m {h\left( {{s_{1i}}} \right) - h\left( {{z_{Ni}}} \right) + h\left( {{y_{Ni}}\left| {{s_{Ni}}} \right.} \right) - h\left( {{z_{Ni}}} \right)} + }\\ {\sum\limits_{n = 1}^{N - 1} {\sum\limits_{i = 1}^m {\left[ {h\left( {{y_{ni}}\left| {{s_{ni}}} \right.} \right) - h\left( {{z_{ni}}} \right)} \right] + m{\varepsilon _m}} } } \end{array} $ | (20) |
其中h()表示熵.由于收到额外的边信息,基于精灵辅助的N用户CGZIC信道容量构成N用户CGZIC容量的外界.因此,可以通过计算基于精灵辅助N用户CGZIC的信道容量来获得N用户CGZIC的另一条速率外界.对于一条长度为m的信息序列,基于精灵辅助的N用户CGZIC的和速率满足式(20).定义E[|xni2|]=Pni, n∈{1, 2, …, N}, i∈{1, 2, …, m},可以得到
| $ \begin{array}{*{20}{c}} {\frac{1}{m}\sum\limits_{i = 1}^m {h{{\left( {{y_{1i}}\left| {{s_{1i}}} \right.} \right)}}} \mathop \le \limits^{\left( {\text{a}} \right)} }\\ {\frac{1}{m}\sum\limits_{i = 1}^m {{\rm{lb}}{{\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + {h^2}{P_{2i}} + \frac{{{P_{1i}}}}{{1 + {h^2}{P_{1i}}}}} \right)} \right]}}} \mathop \le \limits^{\left( {\text{b}} \right)} }\\ {{\rm{lb}}{{\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + \frac{{{h^2}}}{m}\sum\limits_{i = 1}^m {{\rm{lb}}{P_{2i}}} + \frac{{\frac{1}{m}\sum\limits_{i = 1}^m {{\rm{lb}}{P_{1i}}} }}{{1 + \frac{{{h^2}}}{m}\sum\limits_{i = 1}^m {{\rm{lb}}{P_{1i}}} }}} \right)} \right]}} \mathop \le \limits^{\left( {\text{c}} \right)} }\\ {{\rm{lb}}{{\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + {h^2}{P_2} + \frac{{{P_1}}}{{1 + {h^2}{P_1}}}} \right)} \right]}} \mathop = \limits^{\left( {\text{d}} \right)} }\\ {{\rm{lb}}\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + {h^2}P + \frac{P}{{1 + {h^2}P}}} \right)} \right]} \end{array} $ | (21) |
定义E[|xni2|]=Pni, n∈{1, 2, …, N}, i∈{1, 2, …, m},可以得到
| $ \begin{array}{*{20}{c}} {\frac{1}{m}\sum\limits_{i = 1}^m {h\left( {{y_{1i}}\left| {{s_{1i}}} \right.} \right)} \le }\\ {\frac{1}{m}\sum\limits_{i = 1}^m {{\rm{lb}}\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + {h^2}{P_{2i}} + \frac{{{P_{1i}}}}{{1 + {h^2}{P_{1i}}}}} \right)} \right] \le } } \end{array} $ | (22) |
| $ {\rm{lb}}\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + \frac{{{h^2}}}{m}\sum\limits_{i = 1}^m {{\rm{lb}}{P_{2i}}} + \frac{{\frac{1}{m}\sum\limits_{i = 1}^m {{\rm{lb}}{P_{1i}}} }}{{1 + \frac{{{h^2}}}{m}\sum\limits_{i = 1}^m {{\rm{lb}}{P_{1i}}} }}} \right)} \right] \le $ | (23) |
| $ {\rm{lb}}\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + {h^2}{P_2} + \frac{{{P_1}}}{{1 + {h^2}{P_1}}}} \right)} \right] = $ | (24) |
| $ {\rm{lb}}\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + {h^2}P + \frac{P}{{1 + {h^2}P}}} \right)} \right] $ | (25) |
根据文献[13]定理1的证明方法,不等式(22)的推导采用了当信号服从循环对称复高斯分布时条件熵取最大值的原理;不等式(23)的推导采用了Jensen不等式原理;不等式(24)成立是因为该函数是随着功率Pn的增加而递增的;由于考虑对称信道,所以等式(25)成立.同理,当1<n≤N-1时,有
| $ \frac{1}{m}\sum\limits_{i = 1}^m {h\left( {{y_{ni}}\left| {{s_{ni}}} \right.} \right)} \le {\rm{lb}}\left[ {{\rm{ \mathsf{ π} e}}\left( {1 + {h^2}P + \frac{P}{{1 + {h^2}P}}} \right)} \right] $ | (26) |
与前面N-1个用户不同,
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N {{R_n}} \le \frac{1}{m}\sum\limits_{i = 1}^m {\left[ {h\left( {{s_{1i}}} \right) - h\left( {{z_{Ni}}} \right) + h\left( {{y_{Ni}}\left| {{s_{Ni}}} \right.} \right) - } \right.} }\\ {\left. {h\left( {{z_{Ni}}} \right)} \right] + \frac{1}{m}\sum\limits_{n = 1}^{N - 1} {\sum\limits_{i = 1}^m {\left[ {h\left( {{y_{ni}}\left| {{s_{ni}}} \right.} \right) - h\left( {{z_{ni}}} \right)} \right] + {\varepsilon _m}} } \le }\\ {\left( {N - 1} \right)\gamma \left( {{h^2}P + \frac{P}{{1 + {h^2}p}}} \right) + \gamma \left( {{h^2}P} \right) + }\\ {\gamma \left( {\frac{P}{{1 + {h^2}p}}} \right) + {\varepsilon _m} = \left( {N - 1} \right)\gamma \left( {{h^2}P + \frac{P}{{1 + {h^2}p}}} \right) + }\\ {\gamma \left( {{h^2}P + P} \right) + {\varepsilon _m}} \end{array} $ | (27) |
随着m→∞,εm→0.证毕.
至此,可以得到另外一条N用户CGZIC的对称速率外界为
| $ {R_{{\rm{UB2}}}} = \frac{{N - 1}}{N}\gamma \left( {{h^2}P + \frac{P}{{1 + {h^2}P}}} \right) + \frac{1}{N}\gamma \left( {P + {h^2}P} \right) $ | (28) |
在β2范围内,将外界Ⅱ与内界进行比较:
| $ \begin{array}{*{20}{c}} {{R_{{\rm{UB2}}}} - {R_{{\rm{IB}}}} = \frac{{N - 1}}{N}\gamma \left( {{h^2}P + \frac{P}{{1 + {h^2}P}}} \right) + }\\ {\frac{1}{N}\gamma \left( {P + {h^2}P} \right) - \gamma \left( {{h^2}P + \frac{1}{{{h^2}}}} \right) + 1 < }\\ {\frac{1}{N}\gamma \left( {\frac{{\left( {1 + {h^2}P + P} \right){h^2}P}}{{{{\left( {1 + {h^2}P} \right)}^2} + P}} - 1} \right) + 1} \end{array} $ | (29) |
虽没能得到与β1范围内同样的结论,但当总用户数量N递增时,对称速率外界Ⅱ与容量限的距离逐渐趋近于1 bit·s-1·Hz-1.由于RIB<RHK,且RHK<RUB2,所以在β1范围内利用HK方案得到N用户CGZIC的速率区域RHK,当总用户数量趋于无穷时,距离容量限约1 bit·s-1·Hz-1.在高信噪比条件(P≫1, h2P≫1)下,且总用户数量趋于无穷时,得到
| $ \begin{array}{*{20}{c}} {\frac{{{R_{{\rm{UB2}}}}}}{{{C_{{\rm{AWGN}}}}}} \approx \max \left\{ {\frac{{\gamma \left( {{h^2}P - 1} \right)}}{{\gamma \left( {P - 1} \right)}},1 - \frac{{\gamma \left( {{h^2}P - 1} \right)}}{{\gamma \left( {P - 1} \right)}}} \right\} = }\\ {\max \left\{ {\alpha ,1 - \alpha } \right\}} \end{array} $ | (30) |
针对CGZIC,计算出了利用速率分裂技术得到的最大速率与该信道容量限之间的距离.通过增加CGZIC的约束条件得出该信道的速率内界,并参考ETW方法,采用2种精灵辅助方案,得出2条速率外界.最后,通过推导速率内外界之差得出:在CGZIC中,中等干扰条件下,利用HK策略所得到的速率RHK距离信道容量小于1 bit·s-1·Hz-1;在弱干扰条件下,随着总用户数量的增加,利用HK策略所得到的速率RHK距离信道容量逐渐逼近1 bit·s-1·Hz-1.
| [1] | Avestimehr A S, El Gamal H, Jafar S A, et al. Introduction to the special issue on interference networks[J]. IEEE Transactions on Information Theory, 2011, 57(5): 2545–2547. doi: 10.1109/TIT.2011.2116530 |
| [2] | Shannon C E. Two-way communication channels[C]//Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley:IEEE Press, 1961:611-644. |
| [3] | Han T, Kobayashi K. A new achievable rate region for the interference channel[J]. IEEE Transactions on Information Theory, 1981, 27(1): 49–60. doi: 10.1109/TIT.1981.1056307 |
| [4] | Sanson I. On achievable rate regions for the Gaussian interference channels[J]. IEEE Transactions on Information Theory, 2004, 50(6): 1345–1356. doi: 10.1109/TIT.2004.828151 |
| [5] | Mohanty K, Varanasi M K. Degrees of freedom of the MIMO Z-interference channel with delayed CSIT[J]. IEEE Communications Letters, 2015, 19(12): 2282–2285. doi: 10.1109/LCOMM.2015.2483584 |
| [6] | Patel A, Reategui F, Imran M A, et al. On bounds for the cognitive multiple access Z-interference channel[C]//IEEE 14th Canadian Workshop on Information Theory (CWIT). St. John's, NL, Canada:IEEE Press, 2015:46-49. |
| [7] | Mohanty K, Varanasi M K. Degrees of freedom region of the MIMO Z-interference channel with mixed CSIT[J]. IEEE Communications Letters, 2016, 20(12): 2422–2425. doi: 10.1109/LCOMM.2016.2553101 |
| [8] | Shang Xiaohu. Partial capacity boundary of parallel Gaussian Z interference channels[C]//IEEE International Symposium on Information Theory (ISIT). Hong Kong, China:IEEE Press, 2015:206-210. |
| [9] | Costa M H M. A third critical point in the achievable region of the Z-Gaussian interference channel[C]//Information Theory and Applications Workshop (ITA). San Diego, CA, USA:IEEE Press, 2014:1-3. |
| [10] | Costa M H M, Nair C. Gaussian z-interference channel:around the corner[C]//Information Theory and Applications Workshop (ITA). La Jolla, CA, USA:IEEE Press, 2016:1-6. |
| [11] | Liu Yuanpeng Erkip E. On the sum capacity of K-user cascade Gaussian Z-interference channel[C]//IEEE International Symposium on Information Theory Proceedings (ISIT). St. Petersburg, Russia:IEEE Press, 2011:1382-1386. |
| [12] | Mohanty K, Varanasi M K. The degrees of freedom region of the 3-user MIMO cyclic Z-interference channel with perfect and delayed CSIT[C]//IEEE International Symposium on Information Theory (ISIT). Hong Kong, China:IEEE Press, 2015:879-883. |
| [13] | Etkin R H, Tse D N C, Wang Hua. Gaussian interference channel capacity to within one bit[J]. IEEE Transactions on Information Theory, 2008, 54(12): 5534–5562. doi: 10.1109/TIT.2008.2006447 |
| [14] | Zhang Bo, Li Yong, Mao Lulu, et al. Rate-splitting based bound-approaching transmission scheme for the two-user symmetric Gaussian interference channel with common messages[J]. Radioengineering, 2012, 21(4): 1194–1201. |
| [15] |
张博, 李勇, 白宝明, 等. 对称循环高斯干扰信道下的速率分裂方案及其可达和速率[J]. 通信学报, 2013(6): 114–121.
Zhang Bo, Li Yong, Bai Baoming, et al. Rate-splitting scheme and its achievable sum-rate for the symmetric cyclic Gaussian interference channel[J]. Journal on Communications, 2013(6): 114–121. |
| [16] |
张博, 李勇, 白宝明, 等. 高斯干扰信道中基于速率分裂的译码次序算法[J]. 电子与信息学报, 2013, 35(6): 1388–1394.
Zhang Bo, Li Yong, Bai Baoming, et al. Decoding order algorithm based on rate-splitting in Gaussian interference channels[J]. Journal of Electronics & Information Technology, 2013, 35(6): 1388–1394. |


