为提高手掌静脉特征识别的准确率和效率,提出了基于特定方向多尺度稀疏编码(DMSC)方法.首先计算全局方向和局部方向,然后利用多尺度Gabor对划分的子区域进行独立的多尺度方向滤波,并使用稀疏编码方法进行特征提取,利用外形编码产生特征矩阵,使用标准化汉明距离方法对特征矩阵进行相似性判断.实验结果表明,DMSC方法的类间区分性较好,识别力和效率高于现有的手掌静脉识别方法.
A palm vein recognition method based on the directional multi-scale sparse coding (DMSC) was proposed to promote the recognition accuracy and operation efficiency. Firstly, the global and local orientation information were calculated from the palm vein region of interest area. Then, the directional multi-scale Gabor filter were convolved in every sub-region independently. Finally, a feature extraction mechanism based on spare coding was implemented, and the feature matrices were formed by appearance-based method. The similarity of two feature matrices were measured by normalized Hamming distance. Experiments show that the proposed DMSC method achieves higher recognition accuracy and operation efficiency than other palm vein recognition methods.
生物特征识别是一种利用人体内在的固有生理特征进行身份识别的技术,目前国内外对指纹、人脸、掌纹、虹膜、签名等生物特征的识别技术进行了充分的研究,手掌静脉特征识别作为其中的一种,因具备特征图案稳定与唯一性、数据采集便利性等优势,逐渐成为该领域研究热点.手掌静脉纹理丰富,可提供较高的身份区分能力,尤其是其纹理存在于表皮之下使得肉眼不可见,在手掌与物体接触后也不留痕迹,不存在泄露的风险.除此之外,利用手部进行身份识别使人感到自然和易接受,可在廉价低分辨率的设备上进行数据采集,因此具有很好的普及潜力.
稀疏编码作为计算机视觉领域一种重要的图像统计算法,其工作方式与哺乳动物视觉皮层工作方式相似,具有空间、方向和频带的局部性,前期的研究这对其进行了大量的研究. Wright等[1]最早提出了一种基于稀疏表示分类的人脸识别方法,对亮度、噪声和遮挡等干扰具有较好的鲁棒性;Yang等[2]提出了基于Gabor变换字典的稀疏表示识别方法;Zhang等[3]提出了稀疏编码中采用规则化l2范数代替规则化l1范数的编码方法;Wang等[4]提出的位置约束线性编码可利用生物特征样本之间存在的约束关系使得规则化编码系数具有稀疏性.尽管这些研究取得了一定的成果,但在手掌静脉特征识别应用方面,仍存在一些关键问题没有解决,包括:多尺度方向滤波对稀疏编码的影响、静脉全局方向特征与局部方向特性的关系、稀疏编码字典的最优化问题等.
针对以上问题,本文提出了一种基于特定方向多尺度稀疏编码的手掌静脉特征识别方法(DMSC, directional multi-scale sparse coding). DMSC方法先将预处理后的手掌静脉感兴趣区域(ROI, region of interest)划分为多个子区域,利用Gaussian-Radon变换分别获得全局方向特性和局部方向特性参数,然后在子区域上使用Gabor变换和稀疏编码方法获得的复合特征,使用外形编码算法将算法输出与已知的特征方向进行比较并形成最终编码. DMSC方法主要分为全局方向判别与Gabor滤波、稀疏编码与同向叠加、外形编码3个步骤.
1) 方向判别与Gabor滤波.将输入的手掌静脉图像进行灰度预处理后提取ROI,对ROI划分多个子区域并分别提取全局ROI的全局纹理方向和各子区域的局部纹理方向,对各子区域使用Gabor变换获得不同方向及不同尺度下的变换域特征.
2) 稀疏编码与同向叠加.对子区域继续划分更小的独立子块,将Gabor滤波器作为编码字典进行稀疏编码,将编码输出中相同方向的输出进行叠加,获得静脉纹理特定方向复合特征.
3) 外形编码.使用外形编码方法提取复合特征中的全局和局部外形索引,分别同第一步中由Gaussian-Radon方法提取的原始图像中的全局与局部方向特征进行比较、编码,最终的到2个输出矩阵,分别为全局特征编码矩阵和局部特征编码矩阵.
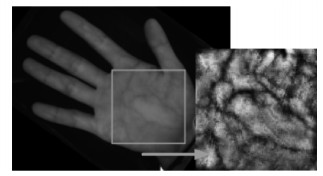
1 特征提取 1.1 方向特征使用波长为700~900 nm的近红外线光源照射手掌可获得静脉纹理图案,经过识别区定位和灰度预处理后可获得ROI图像,如图 1所示.手掌静脉纹理不仅有易见的主要纹理,也有相对细小的纹理,因此具有多尺度特征,可将全局清晰明显的静脉曲线作为强尺度特征,将仅出现在局部的细小静脉曲线作为弱尺度特征.
|
图 1 静脉原始图像及预处理后图像 |
通过观可以发现手掌静脉纹理存在两类方向特性:全局方向特性和局部方向特性[5],如图 2所示.在全局方面表现出的一定的方向趋势称为全局方向特征,如图中所示粗线段.在局部表现出的方向趋势称为局部方向特性,如图中所示细线段.

|
图 2 手掌静脉纹理的方向特性 |
笔者提出的DMSC方法的第一个步骤是获取静脉纹理ROI图像中的方向特征,并作为后续Gabor滤波步骤的参数.将方向特征分为全局方向和局部方向2个层面处理可保留原始图像纹理中的细节位置信息,特别是后续的Gabor滤波对静脉纹理的方向敏感,各子区域按照特定的方向进行滤波处理可获得最优的特征提取效果,从而提高识别系统的准确性. DMSC方法对ROI区域进行了划分,共有N块,其中行数为m,列数为n.若ROI区域为P×P像素,每个子区域划分为L×L像素,且相邻子区域之间重叠T像素,则子区域划分总数量N为
| $ N = {\left[ {\left( {\frac{{P - L}}{{L - T}}} \right) + 1} \right]^2} $ | (1) |
从图像中提取纹理方向信息的一种常用方法是使用Radon变换.对于2D图像,图像中点I(x, y)的Radon变换定义为
| $ \begin{array}{*{20}{c}} {R\left( {k,b} \right)\left[ {I\left( {x,y} \right)} \right]}=\\ {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\mathit{\boldsymbol{I}}\left( {x,y} \right)\delta \left[ {y - \left( {kx + b} \right)} \right]{\rm{d}}x{\rm{d}}y} } } \end{array} $ | (2) |
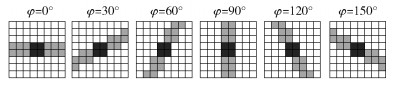
Zhou[6]和Jia[7]基于Radon变换提出的MFRAT算法使用滑动栅格,在确定每个栅格中心的方向权值后使用竞争规则判断线段方向.滑动栅格的定义为ZW2,其中W为矩形栅格的像素宽度,如图 3所示.在栅格ZW2内,线段Lk的定义为Lk={(p, q)|q=k(p-p0)+q0},即由点组成的像素的集合,其中k为斜率.特定斜率(即方向信息)下各滑动栅格的方向可由式(3)确定,其中f(p, q)为Radon变换函数:
| $ {T_f}\left( k \right) = \sum\limits_{\left( {p,q} \right) \in {L_k}} {f\left( {p,q} \right)} $ | (3) |
|
图 3 像素宽度W=8的6方向滑动栅格 |
在此基础上,Zhou[5]提出滑动栅格ZW2内各像素(p, q)与中心点(p0, q0)距离的权重关系,用高斯函数对Radon进行封装,从而形成Gaussian-Radon变换,并成功应用到人体生物特征纹理识别领域中. Gaussian-Radon变换的定义为
| $ G\left( {k,{\sigma _G};{p_0},{q_0}} \right) = \sum\limits_{\left( {p,q} \right) \in {L_k}} {F\left( {p,q} \right)} $ | (4) |
Gaussian-Radon变换的输出结果φ为滑动栅格内各点(p, q)所在的线段方向权重. F(p, q)为由式(5)封装高斯函数的Radon变换:
| $ F\left( {p,q} \right) = f\left( {p,q} \right)\frac{{{G_{{\rm{env}}}}\left( {p,q} \right)}}{{\sum\limits_{\left( {p,q} \right) \in {L_k}} {{G_{{\rm{env}}}}\left( {p,q} \right)} }} $ | (5) |
高斯封装函数的定义如式(6)所示,其中σG控制邻域点对中心点的贡献程度:
| $ {G_{{\rm{env}}}}\left( {p,q} \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}\sigma _G^2}}\exp \left\{ { - \frac{{{{\left( {p - {p_0}} \right)}^2} + {{\left( {q - {q_0}} \right)}^2}}}{{2\sigma _G^2}}} \right\} $ | (6) |
通过移动以(p0, q0)为中心点的滑动栅格并迭代使用式(4),可获得子区域的Gaussian-Radon局部方向特性矩阵L,其元素G(p, q)为各点的方向权重:
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {G\left( {1,1} \right)}&{G\left( {1,2} \right)}& \cdots &{G\left( {1,q} \right)}\\ {G\left( {2,1} \right)}&{G\left( {2,2} \right)}& \cdots &{G\left( {2,q} \right)}\\ \vdots&\vdots&\ddots&\vdots \\ {G\left( {p,1} \right)}&{G\left( {p,2} \right)}& \cdots &{G\left( {p,q} \right)} \end{array}} \right] $ | (7) |
最终,第m行n列子区域的局部特征方向β(m, n)通过矩阵L内元素竞争规则获得:
| $ \beta \left( {m,n} \right) = \mathop {\arg \max }\limits_\varphi \left( {\sum\limits_{x = 1}^p {\sum\limits_{y = 1}^q {\left( {G\left( {x,y} \right) = \varphi } \right)} } } \right) $ | (8) |
同理,若在全部ROI区域内直接使用Gaussian-Radon变换计算方向特性矩阵,则可利用竞争规则获得全局特征方向α:
| $ \alpha = \mathop {\arg \max }\limits_\varphi \left( {\sum\limits_{x = 1}^p {\sum\limits_{y = 1}^q {\left( {G\left( {x,y} \right) = \varphi } \right)} } } \right) $ | (9) |
其中G(x, y)为全部ROI区域内各点的方向权重.
方向数量的选择对系统的最终识别率有重要影响.尽管更多的方向数量可更精确地表达静脉纹理实际方向,但因同一用户的不同静脉图片样本也存在差别,方向数量的增多反而导致识别率的下降,造成系统鲁棒性降低.后续实验证明了当采用12个方向作为可选的方向时,可获得较好的识别率,因此的DMSC方法中φ∈{0°,15°,30°,45°,60°,…,165°}.
1.2 Gabor滤波手掌静脉特征的有效性对识别算法的准确性起着极为重要的作用,采用Gabor滤波器组对静脉提取原始信息的多尺度特征,并将特征编码为稀疏模式,可获得良好的特征模型. Gabor滤波器是计算机视觉领域中一种功能强大的特征分析工具[8],前期的研究已成功地将Gabor滤波器应用于人脸、虹膜、指纹及掌纹识别等应用中.典型的Gabor滤波器是一个具有方向性的复正弦光栅高斯二维调制函数,其数学表达式为
| $ {G_{\sigma ,\mu ,\theta }}\left( {x,y} \right) = {g_\sigma }\left( {x,y} \right)\exp \left\{ {2{\rm{ \mathsf{ π} j}}\mu \left( {x\cos \theta - y\sin \theta } \right)} \right\} $ | (10) |
其中:
| $ {g_\sigma }\left( {x,y} \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}{\sigma ^2}}}\exp \left\{ {\frac{{ - \left( {{x^2} + {y^2}} \right)}}{{2{\sigma ^2}}}} \right\} $ | (11) |
在式(10)和式(11)中,σ表示外部高斯包络的标准方差,μ表示受限正弦光栅的频率,θ表示方向.经过预处理后的手掌静脉图像I[x, y]的Gabor响应由式(12)获得:
| $ {F_{\sigma ,\mu ,\theta }}\left( {x,y} \right) = \mathit{\boldsymbol{I}}\left[ {x,y} \right] * {G_{\sigma ,\mu ,\theta }}\left( {x,y} \right) $ | (12) |
其中:*表示卷积符号. 图 4所示ROI区域经过4个尺度和6个方向的Gabor滤波器组卷积后的响应.

|
图 4 由4尺度6方向构成的Gabor响应 |
DMSC方法中的Gabor滤波器可使用s个尺度参数和n个方向参数.每个划分的子区域中,尺度参数s的数量为预设值,方向参数n为由Gaussian-Radon算法确定的该子区域的局部方向β,因此则经过Gabor滤波后,N个子区域共生成N×n×s个特征块.
1.3 稀疏编码使用Gabor算法对手掌静脉图像滤波后获得的结果具有明显的尺度和方向特性,在非相关尺度与方向上的滤波结果是稀疏的,即具有大量接近0的特征值,可对其进行稀疏编码.稀疏表示涉及到两个问题:字典学习、稀疏编码.通过一系列训练手掌静脉图像用来学习可描述图像的完备基,称为字典学习,良好的字典可较好的描述任意输入的样本特征.通过解决稀疏正则化近似问题,可将系数向量表示为只有很少的几个非零元素,从而稀疏的表示手掌静脉特征. DMSC方法的第2个步骤是对Gabor滤波输出进行稀疏编码,并将不同尺度下相同方向的结果进行叠加.
考虑到Gabor滤波具有明确的物理含义,即其与限定的方向与尺度相关,因此将Gabor滤波器作为描述图像的一组完备基,从而作为稀疏编码的字典,可有效地表达手掌静脉的线段特征,可不必从大量已有的静脉图像中进行字典学习. 图 5显示了一组稀疏编码字典,其中包含4个尺度和6个方向的Gabor滤波.

|
图 5 以Gabor基作为稀疏编码的字典 |
为使编码更准确,DMSC方法将Gabor输出的N×n×s个特征块进行继续划分,将每个子区域划分为m个独立块,并在所有N×n×s×m个独立子块上分别进行稀疏编码.
使用Gabor滤波器建立编码字典D后,对于图像数据X,在编码后信息误差最小的约束下,若编码系数β中非零元素数量最少,则对原始数据X的稀疏编码为
| $ \min {\left\| \beta \right\|_0},{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{D}}\beta } \right\|_2^2 \leqslant \varepsilon ,\beta \in {\mathbb{R}^K} $ | (13) |
其中,‖·‖0和‖·‖2分别表示l0范数和l2范数.式(13)的含义是.利用局部特征方向β作为编码系数向量与编码字典基向量D进行运算所获得的特征向量Dβ,在与原始图像特征向量X充分接近的前提下,应使局部方向β中非零元素的数量最少,即稀疏化.
在式(13)中,最优化问题的求解方法中使用了l0范数,因其是个很难有效处理的非凸优化问题,因此在实际的求解应用中,利用l1范数将原问题转化为凸优化问题,从而求得近似解:
| $ \min {\left\| \beta \right\|_1},{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{D}}\beta } \right\|_2^2 \leqslant \varepsilon ,\beta \in {\mathbb{R}^K} $ | (14) |
文献[9]已经证明,若式(14)式求出的解β为稀疏向量,则式(13)可求出相同的解.此外,还有多种算法可解决这个问题,如内点算法[10]和迭代加权最小二乘法[11]等.
对划分子区域后的手掌静脉Gabor响应图像,应先对每一个子区域进行零均值处理,然后再进行稀疏编码.假设当前第i行第j列独立子块为Xij,使用Gabor完备基作为编码字典D,则该独立子块的稀疏编码系数βij可由式(15)获得[12]:
| $ \mathop {\min }\limits_{{\beta _{ij}}} \left\| {{\mathit{\boldsymbol{X}}_{ij}} - \mathit{\boldsymbol{D}}{\beta _{ij}}} \right\|_2^2 + \lambda {\left\| {{\beta _{ij}}} \right\|_1} $ | (15) |
其中βij为该独立子块中的稀疏编码系数向量.通过引入合适的代价函数λ,可使式(15)与式(14)具有相同的解.
为解决含有零元素的βij向量无法通过l1正则化进行微分的问题,可利用快速迭代收缩阈值方法(FISTA方法)对式(15)进行最优化[13].通过引入向量yk,使其为当前βij的近似值,令Φ为约束方程f(βij)=‖Xij-Dβij‖22梯度的Lipschitz常数,使用式(13)在yk点对‖Xij-Dβij‖22+λ‖βij‖1进行二次逼近:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_L}\left( {{\beta _{ij}},{\mathit{\boldsymbol{y}}_k}} \right) = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{k}} \right) + \left\langle {{\beta _{ij}} - {\mathit{\boldsymbol{y}}_k},\nabla \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{y}}_k}} \right)} \right\rangle + }\\ {\frac{\mathit{\Phi }}{2}\left\| {{\beta _{ij}} - {\mathit{\boldsymbol{y}}_k}} \right\|_2^2 + \lambda {{\left\| {{\beta _{ij}}} \right\|}_1}} \end{array} $ | (16) |
经k+1步迭代使
DMSC方法的第3个步骤是利用外形编码方法[14]提取复合特征中的全局和局部外形索引,并将这两个索引分别与第1步中由Gaussian-Radon方法提取的原始图像中的全局方向特征α和局部方向特征β进行比较、编码,得到两个输出矩阵分别为全局特征编码矩阵Gmap和局部特征编码矩阵Lmap.
使用外形编码的目的是将特定方向的复合特征转换为二进制特征向量.各独立子块同向叠加后,复合特征ψij的方向可由稀疏点的最小纹理响应方向确定.若令ψijα表示复合特征中点(i,j)在全局方向α上的纹理相应,使用竞争策略确定全局外形索引Aij:
| $ {\mathit{\boldsymbol{A}}_{ij}} = \mathop {\arg \max }\limits_\alpha \psi _{ij}^\alpha $ | (17) |
将外形索引Aij与手掌静脉图像的主特征方向α进行二进制编码,当两者差不大于特定阈值δ1时,该像素位置编码为1,否则为0,从而得到全局方向特征的二进制编码G(i, j)为
| $ G\left( {i,j} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;{\rm{if}}\;\left| {\alpha - {\mathit{\boldsymbol{A}}_{ij}}} \right| < {\delta _1}\\ 0,\;\;\;\;其他 \end{array} \right. $ | (18) |
同理,在每个复合特征ψij区域内,点(i,j)在局部方向β上,阈值为δ2时,局部外形索引Bij和局部方向特征的二进制编码L(i, j)为
| $ {\mathit{\boldsymbol{B}}_{ij}} = \mathop {\arg \min }\limits_\beta \psi _{ij}^\beta $ | (19) |
| $ L\left( {i,j} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;{\rm{if}}\;\left| {\beta - {\mathit{\boldsymbol{B}}_{ij}}} \right| < {\delta _2}\\ 0,\;\;\;\;其他 \end{array} \right. $ | (20) |
最终的DMSC编码包含有全局方向和局部方向共2个特征矩阵,各矩阵包含N×s×m个特征块.其中全局方向特征矩阵为Gmap={G1,1,1(i, j), G1, 1, 2(i, j), …, Gu, v, w(i, j)},局部方向特征矩阵为Lmap={L1,1,1(i, j), L1,1,2(i, j), …, Lu, v, w(i, j)},其中u=1, 2, …, N,v=1, 2, …, s,w=1, 2, …, m.
2 特征识别使用标准化汉明距离方法[15]可对DMSC编码生成的Gmap和Lmap特征矩阵进行匹配判别.由于同一个用户的多张手掌静脉样本可能存在轻微的位置变化,因此利用标准化汉明距离方法还可减少匹配判别时因样本轻微位移变化所导致的“弃真”错误.
若P和Q为两个待比较的特征矩阵组,Pg、Pl和Qg、Ql分别代表来自P和Q中由DMSC编码产生的全局方向特征矩阵和局部方向特征矩阵,⊗表示布尔异或运算,则标准化汉明距离可表示为
| $ \mathop {\min }\limits_{\left| s \right| < S,\left| t \right| < T} \frac{{\sum\limits_{i = \max \left( {1,1 + s} \right)}^{\max \left( {N,N + s} \right)} {\sum\limits_{j = \max \left( {1,1 + t} \right)}^{\max \left( {N,N + t} \right)} {\left[ {{\mathit{\boldsymbol{P}}_g}\left( {i + s,j + t} \right) \otimes {\mathit{\boldsymbol{Q}}_g}\left( {i,j} \right) + {\mathit{\boldsymbol{P}}_1}\left( {i + s,j + t} \right) \otimes {\mathit{\boldsymbol{Q}}_1}\left( {i,j} \right)} \right]} } }}{{2H\left( s \right)H\left( t \right)}} $ | (21) |
其中,N×N表示特征矩阵的大小,S和T决定在水平和垂直方向上最大可容忍的像素位移偏差,H(x)=min (N, N+x)-max (1, 1+ x),x∈{s, t}.式(21)对所有可能的S和T取值并计算距离,取最小距离值作为最终结果.距离运算结果取值范围在0~1之间,距离为0表示矩阵P和Q完全相等.
3 实验与分析 3.1 实验数据库使用CASIA和PolyU手掌静脉特征数据库对提出的DMSC方法进行验证. CASIA数据库中包含了来自100个不同用户的共7 200张手掌多光谱图片,分为460、630、700、850、940 nm和白色光共六类采集光源. PolyU多光谱数据库包含用近红外光源组采集的250个用户的手掌静脉图像,分两个时间段共采集6 000张.
根据手掌静脉可吸收近红外线光线的特点,选择CASIC库中940 nm的图像和PolyU作为实验数据库组成.由于每个人左手和右手的手掌静脉纹理图案完全独立,实验将同一个用户的左手和右手图像认为是来自不同的用户,从而增加实验数据库中的用户数量. PolyU库中两个阶段采集的数据来自相同的用户,因此仅采用其中第一阶段采集的数据作为实验数据源.因此,实验数据库包含共700个用户的4 200张手掌静脉图像,每个用户含6张图像,所有图像经过双线性插值的方法将提取到的ROI区统一为512×512像素的灰度图像.
实验中,每张图像均和实验数据库中的其他图像进行比较.实验数据库中包含的用户数量为N=700,每个用户包含样本数量C=6,因此类内比对的数量为N×C!/2×(C-2)!=105 000个,类间比对的数量为C2×N×(N-1)/2=8 807 400个.
3.2 参数选择通过调整DMSC方法中的参数,测试对最终识别效果的影响,从而确定最优的参数组合.在DMSC方法中,有2个重要的参数会对最终的手掌静脉特征识别效果产生较大的影响:Gabor滤波前ROI子区域划分大小和稀疏编码字典D中尺度和方向组合的数量.
表 1显示了ROI子区域划分策略对识别系统等错误率的影响.通过分别比较对子区域进行8×8、16×16、32×32和64×64像素子区域划分和测试可见,当划分策略为32×32像素时,系统等错误率(EER, equal error rate)达到最低的0.10%,为各项实验中最优结果.手掌静脉实验样本ROI图像尺寸为512×512像素,过大的子区域划分会丢失导致静脉纹理的空间信息,过小的子区域划分会产生过于碎片化的Gabor响应,造成后续的稀疏编码中无法准确选取滤波系数.
|
|
表 1 ROI子区域划分策略对识别系统等错误率的影响 |
表 2显示了稀疏编码中字典D元素数量与识别性能的关系.表中所列的为使用不同方向和不同尺度Gabor滤波器作为稀疏编码的基.当Gabor滤波器方向参数数量为12个,分别为0°、15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°,尺度参数取数量为9个,分别为
|
|
表 2 稀疏编码中字典D元素数量与识别性能的关系 |
通过计算类内和类间图像特征距离,验证标准化后的汉明距离对DMSC编码生成的Gmap和Lmap特征矩阵的匹配判别能力.其中,类内匹配计算同一用户的不同注册图像之间的距离,理想情况下特征距离应全部小于门限.类间匹配计算同一用户下所有注册图像与其他用户的所有图像的特征距离,理想情况下特征距离应全部大于门限.
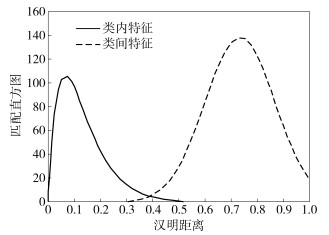
图 6显示了对实验数据库中手掌静脉特征样本进行类内与类间匹配的距离直方图.图中实线表示类内匹配分布,即相同用户的多张注册样本之间的距离分布,虚线表示类间匹配分布,即不同用户之间的样本距离分布.类内分布明显比类间分布距离值小,说明同一用户的不同样本之间特征距离明显小于不同用户的样本距离.两条曲线的相交位置,即汉明距离约为0.4,可作为判别类内与类间特征的门限.
|
图 6 汉明距离匹配直方图 |
实验通过设置不同的水平方向和垂直方向的最大可容忍像素偏差,测试对标准化汉明距离测量方法的鲁棒性.
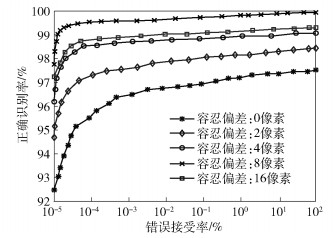
图 7显示了不同的最大容忍像素偏差值的感受性曲线(ROC, receiver operating characteristic),该曲线反应识别系统的错误接受率(FAR, false acceptance rate)和正确接受率(GAR, genuine acceptance rate).可见当容忍偏差在8个像素时,系统的性能最优.这是因为过小的容忍像素偏差值无法纠正同一用户不同注册静脉图像之间的轻微位置偏离,而过大的值会导致不同用户间的静脉纹理位置特征发生混淆,从而降低系统识别率.
|
图 7 最大容忍像素偏差值ROC曲线 |
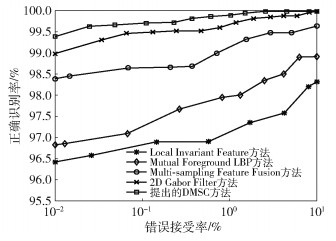
利用实验数据库,将DMSC方法与近年来主流的手掌静脉识别方法Local Invariant Feature[16]、Mutual Foreground LBP[17]、Multi-sampling Feature Fusion[18]和2D Gabor Filter[8]进行比较,以ROC形式显示测试结果,如图 8所示.通过平衡FAR和GAR获得系统EER,如表 3所示.
|
图 8 现有手掌静脉识别方法ROC曲线比较 |
|
|
表 3 手掌静脉识别方法识别效果比较 |
实验计算机硬件环境为Intel i5-4690 CPU、8 GB内存,软件环境为Windows 64位操作系统、Matlab 8.6仿真平台,通过对上述算法迭代1 000次取平均运行时间,计算各算法的运算效率,如表 4所示.在相同的实验环境下,通过记录DMSC方法中各主要算法的运行时间,测试各种算法对特征提取效率的影响,如表 5所示.
|
|
表 4 手掌静脉识别方法特征提取与识别速度比较 |
|
|
表 5 DMSC方法中各主要算法的时间消耗 |
上述算法中,Local Invariant Feature先利用DOG和直方图均衡化方法解决处理图片中光照不均匀的问题,然后使用RootSIFT算法提取静脉特征,该方法尽管运算效率高,但要求手掌静脉图像具有非常高的质量,因此实际测试中识别率不理想;Mutual Foreground LBP先利用基于梯度的最大主曲率算法提取特征,再用MF_LBP算法测量特征之间的距离,该方法虽然可以有效提取局部纹理特征,但无法获取宏观纹理走向信息;Multi-sampling Feature Fusion用多张手掌静脉图片进行特征级信息融合,用双向匹配方法进行特征验证,该方法的识别准确性依赖于融合的图片数量,因此当用户模板数量较少时识别率不理想;2D Gabor Filter提取Gabor滤波的实部和虚部响应后统一编码,但该编码鲁棒性低,当图像轻微改变时Gabor虚部响应变化较大,从而对编码结果产生影响.通过比较可知,DMSC方法综合考虑了手掌静脉纹理的全局特征和局部特征,使用Gabor响应作为稀疏编码字典并对原始数据进行分块处理,无论从识别准确率上还是运行效率上都是最优的.
4 结束语为提高手掌静脉特征提取与识别的识别准确率和运算效率,提出基于特定方向多尺度稀疏编码方法.方法从手掌静脉图像ROI区域中提取全局方向和局部方向特征,利用稀疏编码对Gabor滤波器产生的多尺度滤波相应进行编码,在合并同方向稀疏编码后利用外形编码产生最终的特征矩阵.实验结果表明,该方法的类间区分性较好,识别能力高于现有主流的手掌静脉识别方法.
| [1] | Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210–27. doi: 10.1109/TPAMI.2008.79 |
| [2] | Yang M, Zhang L. Gabor feature based sparse representation for face recognition with gabor occlusion dictionary[C]//2010 European Conference on Computer Vision (ECCV 2010). Kostas Daniilidis:Springer, 2010:448-461. |
| [3] | Zhang L, Yang M, Feng XC. Sparse representation or collaborative representation:Which helps face recognition?[C]//2011 IEEE International Conference on Computer Vision (ICCV 2011). Barcelona:IEEE Press, 2011:471-478. |
| [4] | Wang J J, Yang J C, Yu K, et al. Locality-constrained linear coding for image classification[C]//2010 Computer Vision and Pattern Recognition (CVPR 2010). San Francisco:IEEE Press, 2010:3360-3367. |
| [5] | Zhou Y J, Liu Y Q, Feng Q J, et al. Palm-vein classification based on principal orientation features[J]. PLoS One, 2014, 9(11): e112429–e112429. doi: 10.1371/journal.pone.0112429 |
| [6] | Zhou Y B, Kumar A. Human identification using palm-vein images[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(4): 1259–1274. doi: 10.1109/TIFS.2011.2158423 |
| [7] | Jia W, Huang D S, Zhang D. Palmprint verification based on robust line orientation code[J]. Pattern Recognition, 2008, 41(5): 1504–1513. doi: 10.1016/j.patcog.2007.10.011 |
| [8] | Lee J C, Lee C H, Hsu C B, et al. Dorsal hand vein recognition based on 2D Gabor filters[J]. The Imaging Science Journal, 2014, 62(3): 127–138. doi: 10.1179/1743131X12Y.0000000049 |
| [9] | Candes E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207–1223. doi: 10.1002/(ISSN)1097-0312 |
| [10] | Koh K, Kim S J, Boyd S. An interior-point method for large-scale L1-regularized logistic regression[J]. Journal of Machine Learning Research, 2007, 2007(8): 1519–1555. |
| [11] | Gorodnitsky I F, Rao B D. Sparse signal reconstruction from limited data using focuss:a re-weighted minimum norm algorithm[J]. IEEE Transactions on Signal Processing, 1997, 45(3): 600–616. doi: 10.1109/78.558475 |
| [12] | Zuo W M, Lin Z C, Guo Z H, et al. The multiscale competitive code via sparse representation for palmprint verification[C]//2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2010). San Francisco:IEEE Press, 2010:2265-2272. |
| [13] | Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183–202. doi: 10.1137/080716542 |
| [14] | Cunha A L, Zhou J P, Do M N. The nonsubsampled contourlet transform:theory, design, and applications[J]. IEEE Transactions on Image Processing, 2006, 15(10): 3089–3101. doi: 10.1109/TIP.2006.877507 |
| [15] | Han W Y, Lee J C. Palm vein recognition using adaptive Gabor filter[J]. Expert Systems with Applications, 2012, 39(18): 13225–13234. doi: 10.1016/j.eswa.2012.05.079 |
| [16] | Kang W X, Liu Y, Wu Q X, et al. Contact-free palm-vein recognition based on local invariant features[J]. Plos One, 2014, 9(5): 1239–1245. |
| [17] | Kang W X, Wu Q X. Contactless palm vein recognition using a mutual foreground-based local binary pattern[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(11): 1974–1985. doi: 10.1109/TIFS.2014.2361020 |
| [18] | Yan X K, Kang W X, Deng F Q, et al. Palm vein recognition based on multi-sampling and feature-level fusion[J]. Neurocomputing, 2015, 151(151): 798–807. |


